| 文昌油田水驱砂岩油藏驱油效率评价方法探讨 |
文昌A油田位于海南省文昌市以东海域,油田位于珠江口盆地。主力油藏Ⅱ油组为潮坪沉积,属高孔高渗储层,平均孔隙度26.8%,平均渗透率504.8×10-3 μm2,砂岩厚度多大于20 m,全区稳定分布;地面原油密度较低,为轻质油;Ⅱ油组产能旺盛,地层能量充足,利用天然水驱开发,开发效果较好。早期岩心测定驱油效率与油藏目前采出程度存在矛盾:1999年,利用探井在Ⅱ油组主驱替流线上所取岩心开展室内水驱油实验,岩心孔隙度27.5%,渗透率670×10-3 μm2,测定水驱驱油效率仅57.21%,远低于油藏目前采出程度67.9%。2013年利用文昌A油田密闭取心井在Ⅱ油组强水洗段所取岩心进行饱和度测井,结果表明Ⅱ油组还存在较多剩余油;利用主驱替流线上新取岩心开展室内水驱油实验,岩心孔隙度27.7%,渗透率689×10-3 μm2,测定水驱油效率高达81.73%,说明油藏在不同开发阶段的水驱油效率不同,长期水驱冲刷导致水驱油效率有所提高。为了动态表征油藏驱油效率,在水驱油微观机理研究基础上,创新建立了一套物理模拟与油藏工程方法相结合的动态驱油效率评价技术。
1 动态驱油效率机理及计算方法 1.1 水驱过程储层微观特征变化影响水驱油效率的主要因素为储层孔隙结构、流体性质及驱替条件,在流体性质和驱替条件一定时,孔隙结构的变化必然导致驱油效率的变化。原有储层在开发后期长期水驱冲刷后,孔隙结构特征可能会因为矿物颗粒被冲刷迁移、黏土薄膜脱落等发生明显变化,导致物性及渗流能力变化,润湿性更加亲水[1-2]。根据大庆喇萨杏油田开发后期密闭取心井饱和度测试资料,强水洗部位的平均驱油效率已达到64.22%,尤其注水井周围、油藏强水洗段、“大孔道”等部位剩余油饱和度较低,部分岩心驱油效率达到80% ~90%,大于实验室早期测定水驱油效率平均值50%[3-4]。英国北海大陆架一些油田利用岩心实验测试水驱残余油饱和度平均值为30%,实际生产中,在良好的水驱波及范围内,水驱残余油饱和度平均值仅为15%[5-7]。
为了探索海相砂岩油藏在水驱油过程中孔隙结构的变化特征,开展了岩心水驱油过程孔隙结构变化机理研究,即进行了岩心水驱前后的CT扫描和电镜扫描。岩心水驱前后CT扫描(图 1)表明,水驱前岩心以小孔隙为主,且孔隙多为零星分布,水驱后岩心形成大孔隙,且孔隙多为连片分布,形成了大的渗流通道;岩心水驱前后电镜扫描(图 2)表明,水驱前岩心孔隙中黏土形态完整,水驱后孔隙壁上的黏土胶结物被冲掉,形成了较大的渗流孔隙通道。水驱油微观研究表明,水驱前后岩石的孔隙大小和分布特征发生了较大的变化,水驱对储层孔隙结构进行了改造,水驱作用使得砂岩中胶结物含量减少,孔喉半径变大,形成了大渗流通道。在水驱油过程的不同阶段,储层的孔隙结构改造程度不同,储层的驱油能力也不同,水驱油效率随着水驱倍数的增加而变化。为了能有效描述水驱砂岩油藏在水驱油各个阶段的驱油效率大小,因此引入了动态水驱油效率新概念。
 |
| 图 1 |
 |
| 图 2 |
1.2 动态驱油效率的定义
传统认为驱油效率是保持不变的,反映的是油藏的综合驱油能力,不考虑阶段性,表现为静态驱油效率ED(式1)。但由于水驱过程中,储层物性、孔隙结构、润湿性和黏土矿物成分等性质是逐渐变化的,例如长期水驱会使得岩心水润湿性增强,进而使孔道壁面附着的油膜厚度发生变化,使得残余油饱和度发生变化,导致水驱油效率逐渐变化[8-11]。因此,储层在水驱各阶段的驱油能力,即驱油效率是不同的,在此引入动态驱油效率ED(ti)(式2)新概念,将动态驱油效率定义为油藏在某个时间点或者时间段的驱油能力,以描述油藏在水驱过程中水驱油效率的变化规律,通常对于不存在储层敏感性伤害的储层,动态驱油效率随着水驱倍数的增加而增加,物理意义公式定义如下:
静态驱油效率:
| $ {E_{\rm{D}}} = \frac{{1 - {S_{{\rm{wi}}}} - {S_{{\rm{or}}}}}}{{1 - {S_{{\rm{wi}}}}}} $ | (1) |
动态驱油效率:
| $ {E_{\rm{D}}}\left( {{t_{\rm{i}}}} \right) = \frac{{1 - {S_{{\rm{wi}}}} - {S_{{\rm{or}}}}\left( {{t_{\rm{i}}}} \right)}}{{1 - {S_{{\rm{wi}}}}}}{\rm{ }} $ | (2) |
式中:ED为静态驱油效率,%;ED(ti)为动态驱油效率,%;Swi为束缚水饱和度,%;Sor为残余油饱和度,%;Sor(ti)为动态残余油饱和度,%。
从上式中可以看出,动态驱油效率与静态驱油效率的差异性在于是否考虑时间性,动态驱油效率体现的是岩心在不同水驱油阶段的驱油效率的集合,因此,如果用某个阶段所取岩心测定的水驱油效率来描述油藏的整体水驱油效率是不合理的。动态驱油效率的引入较好地解释了文昌油田早期岩心驱油效率测定值低于最新岩心驱油效率测定值的原因,即长时间的水洗使得油藏的驱油效率从57.21%增加到了81.73%,这表明文昌海相水驱砂岩油藏经过长时间的水驱冲刷改造后,水驱油效率可以达到较高水平。
1.3 利用改进的分形动态相渗计算动态驱油效率为了获得油藏在实际生产过程中各个阶段的动态水驱油效率值,建立了一套以物理模拟与油藏工程方法相结合的动态驱油效率评价技术。为求取油藏动态驱油效率,需先计算油藏水驱油各阶段的动态相渗曲线。1941年,Leverett成功推导了分流量方程,在此基础上推出了分形维动态相渗曲线计算公式,只需根据油藏实际的生产数据,包括产油量、产水量及含水率等,先解出分形维,就可以计算(式3、式4)出油藏的分形维动态相渗曲线[12-15]。但传统分形方程计算的相渗曲线残余油饱和度端点总是收敛于1,因此对此进行了改进,利用物理模拟岩心驱油效率值对其进行端点标定,反算出油藏极限含水率(式5),进而利用水相分流量方程确定所有相渗曲线的残余油饱和度端点(式6),最后计算出动态驱油效率(式2)。
| $ {K_{{\rm{ro}}}} = {\left( {1 - {S_{\rm{D}}}} \right)^2}\left[ {1 - {S_{\rm{D}}}^{\frac{{5 - {D_f}}}{{3 - {D_f}}}}} \right] $ | (3) |
| $ {K_{{\rm{r}}w}}{\rm{ = }}{S_{\rm{D}}}^{\frac{{11 - 3{D_f}}}{{3 - {D_f}}}} $ | (4) |
| $ {f_{{\rm{w极限}}}} = \frac{1}{{\frac{{{\mu _{\rm{w}}}}}{{{\mu _{\rm{o}}}}}a{e^{ - bSor}} + 1}} $ | (5) |
| $ {S_{{\rm{or}}}}\left( {{t_{\rm{i}}}} \right) = - \frac{1}{b}\ln \left[ {\left( {\frac{1}{{{f_{{\rm{w极限}}}}}} - 1} \right)\frac{1}{a}\frac{{{\mu _{\rm{o}}}}}{{{\mu _{\rm{w}}}}}} \right] $ | (6) |
式中:Kro,Krw分别为油相、水相相对渗透率,小数;SD为油藏平均含水饱和度,%;Df为分形维,fw极限为极限含水率,%;μw、μo分别为水、油相黏度,mPa·s;a,b为相渗曲线回归参数。
2 文昌油田动态驱油效率计算及应用 2.1 动态驱油效率计算结果及分析以文昌A油田Ⅱ油组为例,通过利用油藏实际生产数据计算了油藏分形动态相渗曲线,并用2013年Ⅱ油组岩心水驱油效率值81.73%对动态相渗曲线进行标定,最终得到文昌A油田Ⅱ油组开发过程每一年的动态相渗曲线(图 3)。动态相渗曲线形态表现出随着油藏的开采,油相相对渗透率曲线逐渐抬高,水相相对渗透率曲线逐渐压低,两相共渗点逐渐向右偏移,这表明随着油藏的生产,亲水性越来越强,还表现出残余油饱和度端点逐渐向右偏移。根据动态相渗曲线计算的分流曲线(图 4)变化形态表明,随着油藏的生产,分流曲线向右偏移,含水上升趋势越来越缓,开发效果越来越好。
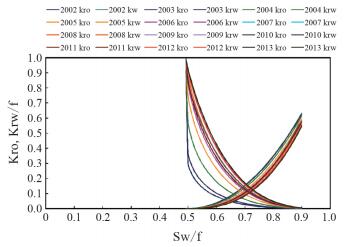 |
| 图 3 Ⅱ油组动态相渗曲线 |
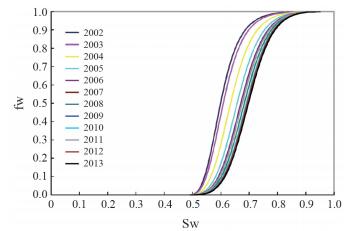 |
| 图 4 Ⅱ油组动态分流曲线 |
根据Ⅱ油组分形动态相渗曲线计算了相应的动态驱油效率值,计算结果表明,Ⅱ油组随着水驱的进行,动态驱油效率从投产初期的55%逐渐增加到目前的81.73%,增加幅度47.2%,从动态驱油效率和水驱倍数的关系曲线(图 5)可以看出,动态驱油效率是随着水驱倍数的增加而逐渐增加的,并且表现出很好的正对数关系ED=5.471 8 Ln(HPV) +80.563,两者相关系数达到了0.961 7。水驱油过程是对砂岩油藏储层的改造过程,随着润湿性、孔喉结构、物性等性质的变化,水驱油效率是变化的,具体表现为驱油效率随着水驱倍数的增加而增加。
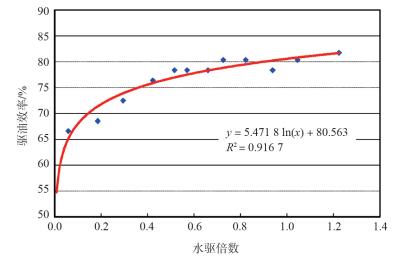 |
| 图 5 Ⅱ油组动态驱油效率与油藏水驱倍数关系曲线 |
Ⅱ油组从2002年投产至今的动态驱油效率值介于2001年岩心驱油效率和2013年岩心驱油效率之间(表 1),可见动态驱油效率具有可变性。通过引入动态驱油效率新概念,量化表征了水驱过程储层性质的变化规律。将动态驱油效率应用于数值模拟研究中,将使数值模型动态化,实现精细化数值模拟研究,更准确认识油藏开发潜力。
| 表 1 Ⅱ油组驱油效率汇总 |
2.2 创新建立油藏数值模拟渗流动态模型
传统的油藏数值模拟研究中,在一定的区域内仅使用一条相渗曲线进行模拟,使得该区域内储层的两相渗流特征和驱油效率是恒定的,建立的是两相渗流静态模型,不符合油藏开采过程中渗流特征可变化性。通过将动态驱油效率研究成果应用于油藏数值模拟研究中,创新建立了数值模拟渗流动态模型。以文昌A油田Ⅱ油组为例,将油藏分形动态相渗曲线和动态驱油效率应用到数值模拟研究中,建立了两相渗流动态模型,具体方法是分时间段在油藏使用了不同的相渗曲线和不同的驱油效率值,使得储层的两相渗流特征和驱油效率是随时间发生改变的。在模拟过程中修改参数基本一致情况下,通过对比静态渗流模型和动态渗流模型在同一时间的剩余油分布剖面(图 6)可以看出,静态模型被水体驱替过的区域含油饱和度为一定值16.5%,而动态模型被水体驱替过的区域含油饱和度具有渐变性,为16.2% ~ 25.3%,具有非均匀驱替的效果。同时期开发井RPM饱和度测井结果显示,水淹区含油饱和度16.0% ~ 27.2%,通过对比表明,动态模型更符合油藏实际非均匀水驱规律,提高了数值模拟研究的精度,能更好指导老油田挖潜工作的开展。
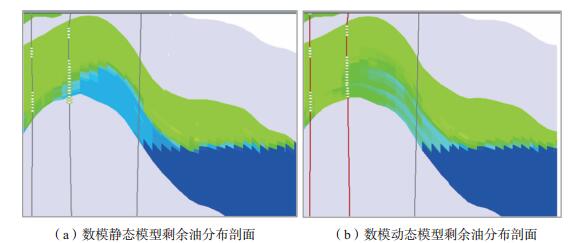 |
| 图 6 |
3 结论
(1) 水驱油过程是对砂岩油藏储层的改造过程,长时间的水驱作用将使岩石润湿性、孔喉结构和物性等性质发生很大的变化。
(2) 动态驱油效率反映的是油藏在某个时间点或者时间段的驱油能力,定量表征了油藏水驱过程的储层改造作用,对于不存在储层敏感性伤害的储层,动态驱油效率随着水驱倍数的增加而增加。
(3) 文昌油田动态相渗曲线和动态驱油效率变化规律表明,海相砂岩油藏在经过长时间的水驱后,储层孔隙结构变好,驱油效率增加,开发效果越来越好。
(4) 通过将动态驱油效率应用于油藏数值模拟研究中,构建了油藏数值模拟两相渗流动态模型,创新性形成了数值模拟非均匀驱替模式,与传统数值模拟两相渗流静态模型的均匀驱替模式相比较,更符合油藏的实际开发规律。
| [1] |
成方, 等. 高含水阶段重新认识水驱油效率[J]. 实验勘探与开发, 2012, 39(3): 338-345. |
| [2] |
何更生. 油层物理[M]. 北京: 石油工业出版社, 1994: 23-29.
|
| [3] |
兰玉波, 赵永胜, 魏国章. 矿场密闭取心与室内模拟的驱油效率分析[J]. 大庆石油学院学报, 2005, 29(4): 43-45. DOI:10.3969/j.issn.2095-4107.2005.04.015 |
| [4] |
李传亮. 油藏工程原理[M]. 北京: 石油工业出版社, 2005: 79-85.
|
| [5] |
Jayasekera A J, Goodyear S G. Improved Hydrocarbon Recovery in the United Kingdom Continental Shelf: Past, Present and Future//Proceedings of the SPE/DOE Improved Oil Recovery Symposium[C]. Tulsa, Oklahoma: SPE, 2002.
|
| [6] |
王尤富, 鲍颖. 油层岩石的孔隙结构与驱油效率的关系[J]. 河南石油, 1999, 13(1): 23-25. |
| [7] |
蔡忠. 储集层孔隙结构与驱油效率关系研究[J]. 石油勘探与开发, 2000, 27(6): 45-46, 49. DOI:10.3321/j.issn:1000-0747.2000.06.021 |
| [8] |
葛家理. 现代油藏渗流力学原理[M]. 北京: 石油工业出版社, 2002: 28-30.
|
| [9] |
吕建中. 国外石油科技发展报告(2015)[M]. 北京: 石油工业出版社, 2015: 24-30.
|
| [10] |
科林斯R E.流体通过多孔材料的流动[M].陈钟祥, 吴望一, 译.北京: 石油工业出版社, 1984: 105-108.
|
| [11] |
Ikoku C U. Natural Gas Reservoir Engineering. New York, USA: John Wiley & Sons, Inc., 1984.
|
| [12] |
Cole F W. Reservoir Engineering Manual. Houston: Gulf Publishing Co., 1969
|
| [13] |
Blunt M J, Barker J W, Rubin B, et al. Predictive Theory for Viscous Fingering in Compositional Displacement[J]. SPE Reservoir Engineering, 1994, 9(1): 73-80. DOI:10.2118/24129-PA |
| [14] |
Hinkley R E, Davis L A. Capillary Pressure Discontinuities and End Effects in Homogeneous Composite Cores: Effect of Flow Rate and Wettability//Proceedings of the SPE Annual Technical Conference and Exhibition[C]. New Orleans, Louisiana: SPE, 1986.
|
| [15] |
Qadeer S, Dehghani K, Ogbe D O, et al. Correcting Oil/Water Relative Permeability Data for Capillary End Effect in Displacement Experiments//Proceedings of the SPE California Regional Meeting[C]. Long Beach, California: SPE, 1988.
|
 2019, Vol. 39
2019, Vol. 39

