| 页岩岩石物理建模研究 |
我国有非常丰富的页岩气资源, 页岩作为一种广泛发育的沉积岩, 具有自生自储的特殊性质, 使得越来越多的目光聚焦到页岩气储层的研究当中来[1-2]。地震勘探在页岩气勘探中发挥着重要作用, 包括查明页岩的埋藏深度、分布范围、岩层厚度、产状形态等, 并可辅助找到页岩气"甜点区域, 即寻找热成熟度高、有机质丰度高、脆性高、储集空间大、裂缝发育的页岩。其中, 干酪根含量的多少是衡量页岩储量的重要参数之一, 通常干酪根含量高对应高产能页岩, 而泥页岩由于其天然的低孔低渗特性, 使得裂缝对页岩油气的储存和运移能力尤为凸显[3]。充分考虑储层微观特征建立的岩石物理模型, 可以建立储层微观物性特征和宏观弹性性质之间的关系, 为储层定量解释等提供参考依据。通过岩石物理模型可以建立储层参数和地震属性之间的联系, 建立的岩石物理模型需要考虑各种因素, 尽可能准确反映实际的地下介质, 并且要保证输入模型的参数可以实际测量。这是针对页岩气储层进行岩石物理建模的重点, 建模的好坏将影响到测井资料与地震资料解释的精度, 对页岩气储层识别产生一定的影响[4-5]。
1 岩石物理模型类型理论模型是进行岩石物理研究的主要方法之一, 想用理论的方法求得多相混合物的等效弹性性质, 需要知道各组分的弹性模量、体积含量和几何分布等。如果只知道前两者, 就需要通过假设矿物颗粒与孔隙空间的特定排列方式, 把实际的岩石理想化, 根据不同的假设条件可将岩石物理模型分为不同的类型[6-7]。
对各向同性介质来说, 有些模型假设岩石各组分是层状排列的, 如边界模型、Wood方程、Wyllie时间平均方程等; 有些模型假设岩石是由固体颗粒与球状孔隙组成的集合体, 并且孔隙是相互连通的, 如Gassman方程、Biot理论等; 有些模型将某种成分看作岩石中的背景介质, 而其他成分看作镶嵌在背景介质的包含物, 其形状可以是球形、椭球形、硬币形等, 如SCA模型、DEM模型等。
对各向异性介质来说, 由于黏土或裂隙的定向排列, 岩石各向异性程度较强, 如页岩, 具有很强的VTI性质, 采用各向同性岩石物理模型对其进行近似具有一定的局限性。应用比较广泛的几种各向异性等效介质模型, 有各向异性SCA模型、各向异性DEM模型、Brown-Korringa模型、Backus平均模型等。
岩石的物理性质由组分、内部结构、所处热力学环境决定, 实际岩石相对较复杂, 简单的套用某一种理论模型难以准确指导地震定量解释, 甚至会产生误导[1]。因此, 我们要对储层进行岩石物理分析时, 要综合运用各类资料, 对不同类型的储层建立相适应的模型。以页岩来说, 岩石各向异性程度较强, 采用各向同性岩石物理模型对其进行近似具有一定的局限性, 针对各向异性介质建立适当的各向异性岩石物理模型具有较大的研究价值。
2 各向异性DEM建模应用DEM模型进行建模, 通常都是针对双相介质, DEM模型适用于考虑岩石内部连续相同离散相之间的弹性互动[8]。假设把体积是V0的固态矿物相作为背景基质, 向背景基质中加上ΔV的包含物, 同时替换同等体积的矿物相, 得到新的基质, 重复上述过程, 直到各相体积达到一定比例为止, 由此模拟双相介质。Hornby[9]提出各向异性DEM模型的表达式:
| $ \frac{d}{dv}\left( {{c}^{\text{DEM}}}\left( v \right) \right)=\frac{1}{1-v}{{\left( {{c}^{\text{i}}}-{{c}^{\text{DEM}}}\left( v \right) \right)}^{*}}{{\left[ I+\hat{G}\left( {{c}^{\text{i}}}-{{c}^{\text{DEM}}}\left( v \right) \right) \right]}^{-1}} $ | (1) |
式中, v是包含物的体积含量, 小数; I是单位张量,
cDEM代表通过DEM模型得到的等效介质刚度张量, 无量纲; ci代表在基质中加入的包含物的刚度张量, 无量纲;
以Bakken页岩取自同一口井的不同深度处岩心测量出的数据为例。通过各向异性DEM模型建模, 两相介质分别是干酪根和黏土, 其中, 干酪根的体积模量K=2.9 GPa, 剪切模量G=2.7 GPa; 黏土的体积模量K=22.9 GPa, 剪切模量G=10.6 GPa。需要用到关于黏土及干酪根的弹性参数见表 1, 这些参数值是由Vernik和Landis[10-11]通过实验室测量数据推导出来的, 虽然不完全代表真实的干酪根和黏土的相关数值, 但还是可以很好地描述Bakken页岩。
| 表 1 Bakken页岩两相模型参数 |
应用DEM模型进行岩石物理建模研究(图 1)。黑色曲线代表的是以干酪根作为基质, 黏土作为包含物通过DEM建模得到的刚度系数随着干酪根的变化趋势。蓝色曲线代表以干酪根作为包含物加入到黏土基质中建模得到刚度系数与干酪根的变化关系。红色箭头代表包含物纵横比增大的方向, 包含物纵横比分别取值0.1、0.3、0.9。图 1中的点是Bakken页岩的实验室测量数据。
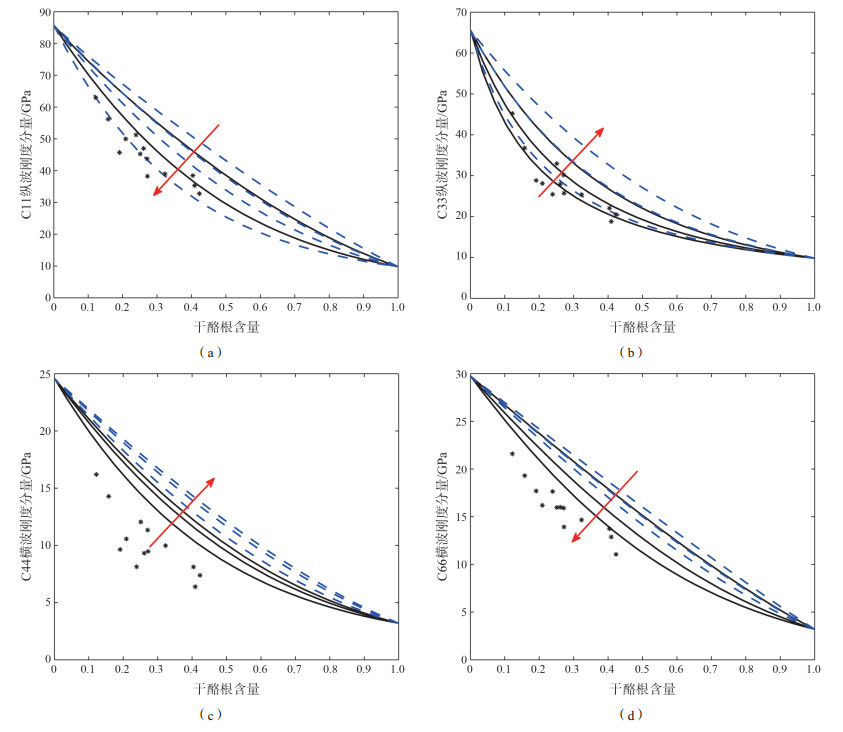 |
| 图 1 采用各向异性DEM模型得到的等效刚度分量(a), (b), (c), (d)随干酪根含量的变化规律 |
图 1(a)中纵坐标C11是纵波刚度分量, 横坐标是干酪根含量。可以看出, C11随着干酪根含量的增加而逐渐减少, 并且随着包含物纵横比增加, 曲线和实际数据越接近。相对来说, 黑色曲线更加接近实验室测量数据, 说明在建模中把干酪根当作基质, 黏土作为包含物加入的建模流程得到的刚度系数结果更佳。
图 1(b)中纵坐标C33是纵波刚度分量。图中可以看出C33随干酪根含量增加而减少, 但是包含物纵横比越小, 曲线与实际数据的吻合度越好。
图 1(c)中纵坐标C44是横波刚度分量。随着包含物纵横比增加, 曲线与实际数据差别越大, 此时用DEM模型得到的结果与实际的实验室测量结果存在一定的误差, 这可能是干酪根同黏土矿物的弹性模量在取值时不够精准造成的。
图 1(d)中C66是横波刚度分量。C66随干酪根含量的增加而减少, 另外, 随着包含物纵横比增加的方向, 预测结果更加接近实验室测量数据。总体来说, 用各向异性DEM模型对Bakken页岩进行预测的方法是适用的。
3 正交各向异性岩石物理建模对页岩气储层进行甜点精确预测, 在进行岩石物理建模过程中要尽可能多地考虑影响页岩各向异性的因素。裂缝就是其中一个很重要的因素, 岩石中是否存在裂缝至关重要。假如往各向同性介质中加入一组或者多组裂缝, 裂缝的类型、数量等差异都会让各向异性的程度有差别, 表现出的各向异性相关性质各异; 各向异性性质不同的介质对应的弹性参数关系也会有差别, 具体问题还需具体分析[3, 12]。比较常见的是定向排列和平行裂缝, 这样的裂缝会表现横向各向同性及方位各向异性。为了更好地分析实际页岩储层的复杂性, 我们提出了针对复杂页岩储层的岩石物理建模流程, 即含裂缝页岩的岩石物理建模。
首先, 进行有机页岩岩石物理建模[13]:(a)将黏土、方解石、石英混合物应用Reuss-VoigtHill平均模型得到"黏土"包含物; (b)使用各向异性DEM模型, 将"黏土"包含物加入干酪根基质中, 得到干酪根和"黏土"的混合物; (c)把得到的干酪根和"黏土"的混合物当作基质, 再运用各向异性DEM模型将孔隙加入其中。根据DEM模型的特点, 通过各向异性DEM模型构建其等效弹性张量与孔隙度、孔隙纵横比的关系式, 将岩石孔隙等效为具有单一纵横比的椭球体, 采用各向异性DEM模型将干燥的孔隙包含物加入到有机页岩基质中, 得到孔隙介质干岩石的等效弹性张量关系式。由此得到的等效介质中"黏土颗粒是离散分布的, 孔隙空间也是彼此隔离的。
在建模过程中用到的各矿物的弹性参数值见表 2。
| 表 2 矿物的弹性参数 |
横向各向同性(TI)是地震领域主要研究的各向异性类型, 介质具有一个主对称轴, 刚度矩阵中含有5个独立的弹性参数。依据其对称轴在三维空间是垂直、水平还是倾斜, 可划分为VTI (Transverse isotropy with a vertical symmetry axis)介质, HTI (Transverse isotropy with a horizontal symmetry axis)介质和TTI (Transverse isotropy with a tilted symmetry axis)介质[7]。通过上述建模流程可以得到VTI页岩模型。该VTI等效介质的刚度系数随着干酪根的变化趋势如图 2, 刚度系数随着干酪根含量的增加而减小, 且刚度系数的变化率随着干酪根含量的增加而减小。干酪根含量的多少直接关系到页岩气产量, 不过在实际的岩石中, 干酪根含量一般在30%以内, 其含量的多少会对刚度系数产生较大的影响, 所以在岩石物理建模中对干酪根的研究显得尤为重要。
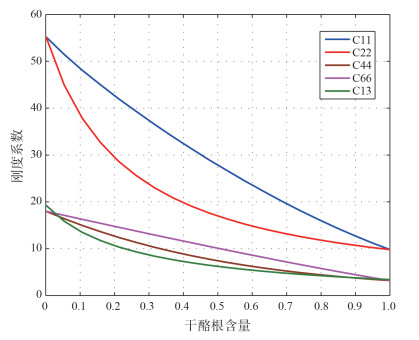 |
| 图 2 建模得到的VTI页岩模型的刚度参数随干酪根的变化 |
正交各向异性介质具有三个相互正交的对称面, 其刚度矩阵中有9个独立的弹性参数。一般认为是由具有垂直对称轴的周期性薄互层(PTL)和具有水平对称轴的垂直裂缝(EDA)组合而成[7]。
在加入垂直裂缝的过程中, 用到了Schoenberg理论[14-15]:把裂缝当作是在地层中存在的高柔性界面, 在这个界面上, 位移是非连续性的, 而应力具有连续性。包含裂缝的岩石柔量S由围岩柔量Sb及裂缝柔量Sf组成, 关系式如下:
| $ S={{S}_{\text{b}}}+{{S}_{\text{f}}} $ | (2) |
利用Schoenberg理论将垂直裂缝加入到VTI围岩介质中, 以构建正交各向异性介质。正交介质的弹性矩阵可通过向导出的VTI介质的刚度矩阵中加入校正矩阵获得。
校正矩阵由3×3的裂缝柔度矩阵表示, 矩阵表示为:
| $ Z=\left\{ \begin{matrix} {{Z}_{\text{N}}}&0&0 \\ 0&{{Z}_{\text{V}}}&0 \\ 0&0&{{Z}_{\text{H}}} \\ \end{matrix} \right\} $ | (3) |
式中, ZN表示法向柔度, ZV表示垂直切向柔度, ZH表示横向切向柔度。
裂缝介质的刚度矩阵可以通过向背景介质的柔度矩阵内加入裂缝柔度矩阵Z, 然后通过取逆的方法求得。得到的刚度矩阵可表示为:
| $ {{c}_{\text{e}}}=\ \left[ \begin{matrix} {{c}_{\text{11}}}_{\text{b}}\left( 1-{{\delta }_{\text{N}}} \right) & {{c}_{\text{13}}}_{\text{b}}\left( 1-{{\delta }_{\text{N}}} \right) & {{c}_{\text{13}}}_{\text{b}}\left( 1-{{\delta }_{\text{N}}} \right) & 0 & 0 & 0 \\ {{c}_{\text{12}}}_{\text{b}}\left( 1-{{\delta }_{\text{N}}} \right) & {{c}_{\text{11}}}_{\text{b}}\left( 1-{{\delta }_{\text{N}}}\frac{c_{12\text{b}}^{2}}{c_{11\text{b}}^{2}} \right) & {{c}_{\text{13}}}_{\text{b}}\left( 1-{{\delta }_{\text{N}}}\frac{{{c}_{\text{12b}}}}{{{c}_{\text{11b}}}} \right) & 0 & 0 & 0 \\ {{c}_{\text{13}}}_{\text{b}}\left( 1-{{\delta }_{\text{N}}} \right) & {{c}_{\text{11}}}_{\text{b}}\left( 1-{{\delta }_{\text{N}}}\frac{c_{12\text{b}}^{2}}{c_{11\text{b}}^{2}} \right) & {{c}_{\text{33}}}_{\text{b}}\left( 1-{{\delta }_{\text{N}}}\frac{c_{13\text{b}}^{2}}{{{c}_{\text{11b}}}{{c}_{\text{13b}}}} \right) & 0 & 0 & 0 \\ 0 & 0 & 0 & {{c}_{\text{44b}}} & 0 & 0 \\ 0 & 0 & 0 & 0 & {{c}_{\text{13}}}_{\text{b}}\left( 1-{{\delta }_{\text{V}}} \right) & 0 \\ 0 & 0 & 0 & 0 & 0 & {{c}_{66}}_{\text{b}}\left( 1-{{\delta }_{\text{H}}} \right) \\ \end{matrix} \right] $ | (4) |
式中,
在完成页岩VTI介质建模后, 一般需要利用定向分布函数, 引入一个压实系数, 将各向异性约束在一个合理的量级内。Owens[16]把黏土包含物的方向分布定义为:
| $ W\left( \Phi \right)=\frac{1}{8{{\mathit{\pi }}^{2}}}\ \frac{{{C}^{2}}}{{{\left( \text{co}{{\text{s}}^{2}}\Phi +{{C}^{2}}\text{si}{{\text{n}}^{2}}\Phi \right)}^{3/2}}} $ | (5) |
式中:C为压实系数, Φ是极化角度。
在此基础上, 往VTI介质中加入一组垂直裂缝, 进行正交各向异性岩石物理建模, 讨论干酪根含量和裂缝对页岩刚度系数的影响。为简单起见, 假设加入的裂缝顺度ZN=ZV=ZH, 最终得到在顺度分别为0.01和0.03时, 刚度参数随干酪根含量的变化分别如图 3(a)和图 3(b)所示, 显然, 在裂缝顺度一定时, 刚度系数的值随着干酪根含量的增加而减少。当干酪根含量不变时, 对比图 3(a)和图 3(b)可以看出, 裂缝顺度的大小整体上降低了刚度系数的值, 但是每个刚度参数减小的程度不完全相同。总之, 干酪根含量和裂缝的存在都会对各向异性的刚度矩阵产生影响, 在之后的研究中会进一步探究干酪根含量和裂缝发育对AVO响应特征产生的影响, 建立起储层特征与地震属性之间的关系, 为反演提供一定的参考依据。
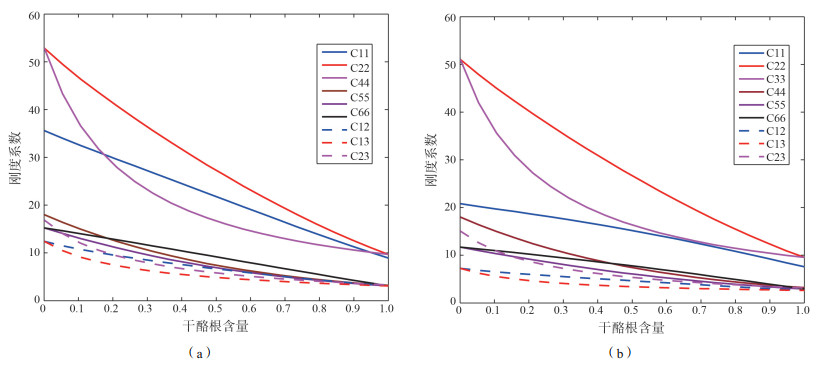 |
| 图 3 刚度矩阵随干酪根含量的变化(a)柔度矩阵为0.01(b)柔度矩阵为0.03 |
4 结论
通过本文研究, 得出以下结论:
(1) 页岩与常规储层存在一定的区别。页岩具有较强的各向异性、孔隙类型多样、矿物成分复杂等, 针对页岩气储层进行的岩石物理建模要尽可能考虑更多的存在因素, 反映比较真实的地下介质情况, 并且模型可操作性要强, 输入参数是可以方便得到的, 但是要考虑到计算成本。
(2) 研究干酪根含量和分布对页岩弹性性质产生的影响时, 针对Bakken页岩的各向异性DEM模型, 把干酪根作为背景介质时预测结果较好。为了更好地建立真实的页岩模型, 尝试在有机页岩岩石物理建模得到VTI岩石模型的基础上, 把垂直裂缝加入到模型中, 构建出了正交各向异性岩石物理模型。
| [1] |
TapanMukerji. 利用统计岩石物理学和地震反演技术作出[J]. 海洋石油, 2000, 20(1): 71-74. |
| [2] |
马淑芳, 韩大匡, 甘利灯, 等. 地震岩石物理模型综述[J]. 地球物理学进展, 2010, 25(2): 460-471. DOI:10.3969/j.issn.1004-2903.2010.02.012 |
| [3] |
解建建.基于横波分裂分析的裂缝检测方法研究及应用[D].成都: 成都理工大学, 2011.
|
| [4] |
刘恩儒, 曾新吾. 裂缝介质的有效弹性常数[J]. 石油地球物理勘探, 2001, 36(1): 37-44. DOI:10.3321/j.issn:1000-7210.2001.01.006 |
| [5] |
林建东, 任森林, 薛明喜, 等. 页岩气地震识别与预测技术[J]. 中国煤炭地质, 2012, 24(8): 56-60. DOI:10.3969/j.issn.1674-1803.2012.08.12 |
| [6] |
原宏壮.各向异性介质岩石物理模型及应用研究[D].北京: 中国石油大学, 2007.
|
| [7] |
Mavko G, Mukerji T, Dvorkin J. The Rock Physics Handbook[M]. Cambridge: Cambridge University Press, 2009.
|
| [8] |
胡起, 陈小宏, 李景叶, 等. 干酪根对富含有机质页岩弹性性质的影响[J]. 地球物理学进展, 2014, 29(2): 748-753. |
| [9] |
Hornby B E, Schwartz L M, Hudson J A. Anisotropic Effective-Medium Modeling of the Elastic Properties of Shales[J]. Geophysics, 1994, 59(10): 1570-1583. DOI:10.1190/1.1443546 |
| [10] |
Vernik L, Liu X Z. Veloci ty Ani sot ropy in Shales:APetrophysicalStudy[J]. Geophysics, 1997, 62(2): 521-532. DOI:10.1190/1.1444162 |
| [11] |
Vernik L, Landis C. Elastic Anisotropy of Source Rocks:Implications for Hydrocarbon Generation and Primary Migration[J]. AAPG Bulletin, 1996, 80(4): 531-544. |
| [12] |
李雪. 裂缝性油气藏储层综合表征体系综述[J]. 中国科技论文, 2015, 10(15): 1861-1870. DOI:10.3969/j.issn.2095-2783.2015.15.023 |
| [13] |
胡起, 陈小宏, 李景叶. 基于单孔隙纵横比模型的有机页岩横波速度预测方法[J]. 地球物理学进展, 2014, 29(5): 2388-2394. |
| [14] |
Schoenberg M, Helbig K. Orthorhombic Media:Modeling Elastic Wave Behavior in A Vertically Fractured Earth[J]. Geophysics, 1997, 62(6): 1954-1974. DOI:10.1190/1.1444297 |
| [15] |
Schoenberg M, Douma J. Elastic Wave Propagation in Media With Parallel Fractures and Aligned Cracks[J]. Geophysical Prospecting, 1988, 36(6): 571-590. DOI:10.1111/gpr.1988.36.issue-6 |
| [16] |
Owens W H. Strain Modification of Angular Density Distributions[J]. Tectonophysics, 1973, 16(3-4): 249-261. DOI:10.1016/0040-1951(73)90014-0 |
 2019, Vol. 39
2019, Vol. 39

