| 莺琼盆地X-X气田束缚水饱和度评价 |
2. 中国石油长城钻探工程有限公司国际测井公司, 北京 100101;
3. 长江大学, 湖北武汉 430100
2. International Logging Company of GWDC, Beijing 100101, China;
3. Yangtze University, Wuhan, Hubei 430100, China
X-X气田黄流组储层岩性主要为浅灰色粉砂岩,少量细砂,本气田黄流组分为Ⅰ、Ⅱ、Ⅲ、Ⅳ四个气组,每个气组均钻遇到好的气层,但整体而言,Ⅰ气组是本气田的主力气组,含气性较好。X-X-A井测井资料处理解释成果图(图 1)显示,黄流组气层测井响应特征明显,表现为低伽马、高电阻率,电阻率在4.1 ~ 81.0 Ω·m;密度中子镜像交会特征明显,密度偏低,密度值为1.84 ~ 2.28 g/cm3;中子也较低,中子值18.0% ~ 34.0%;纵波时差增大,时差值为100.0 ~ 133.0 us/ft。此外,气层段纵横波速度比减小,泊松比减小,体积压缩系数增大。
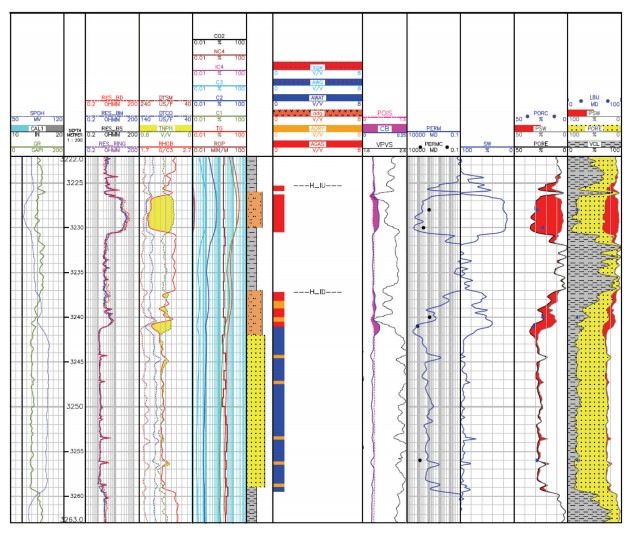 |
| 图 1 X-X-A井测井资料处理解释成果 |
2 莺琼盆地束缚水饱和度与孔隙度和气柱高度的关系
由于在气层中天然气克服毛细管压力作用而进入储层中的多少与气柱高度有关[1],因此在物性好的高阻气层中,含水饱和度随深度的变化不明显;而在低阻气层中,含水饱和度随深度的变化明显。这一特征反映在电阻率曲线上,在物性变化不大的同一层中,电阻率由下到上逐渐变高(图 2)。
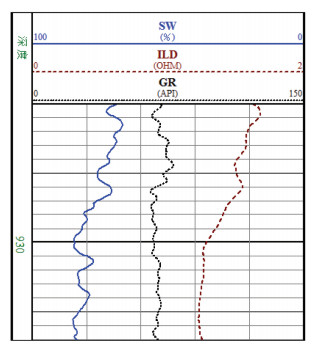 |
| 图 2 含气饱和度随深度的变化 |
气层中,含气饱和度与原始束缚水饱和度之和为100%,因此含气饱和度的变化规律反映了原始束缚水饱和度的变化规律。
在原始气藏条件下,气水密度差所产生的浮力与毛细管压力相平衡[2]:
| $\Delta \rho H={{p}_{\text{cR}}} $ | (1) |
式中:H为气水界面以上高度,m;Δρ为气水密度差,g/cm3;pcR为储藏条件下的毛细管压力,MPa。
因而可以把毛细管压力曲线换成自由水界面以上高度(气柱高度)与含气饱和度的关系曲线,换算关系为[3]:
| $ H=\frac{{{p}_{\text{cR}}}}{{{\rho }_{\text{w}}}-{{\rho }_{\text{g}}}} $ | (2) |
式中:ρw和ρg分别为储藏条件下水与气的密度,g/cm3。
束缚水饱和度与气柱高度有关,尤其是当孔隙结构复杂、孔隙度小、岩石颗粒分选不好时[4]。因此用孔隙度和气柱高度共同反映束缚水饱和度的大小较好。图 3是LD气田不同孔隙度条件下束缚水饱和度与气柱高度关系图,图 4是LD气田不同气柱高度条件下束缚水饱和度与孔隙度关系图。
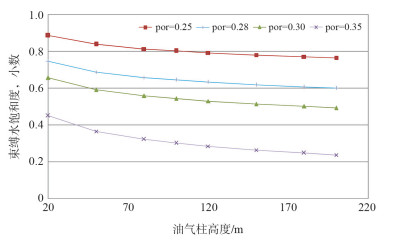 |
| 图 3 不同孔隙度条件下,束缚水饱和度与气柱高度关系 |
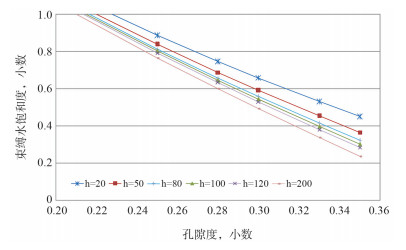 |
| 图 4 不同气柱高度条件下,束缚水饱和度与孔隙度关系 |
从图 3中得知在孔隙度一定的情况下随着气柱高度的增大束缚水饱和度呈指数降低,这种降幅在气柱高度较低时尤其明显。从图 4中得知在油气柱高度一定的情况下随着孔隙度的增大束缚水饱和度降低。由以上分析可知,莺琼地区束缚水饱和度对气柱高度敏感,在计算束缚水饱和度时需考虑油气柱高度影响[5]。
3 利用岩心毛管压力资料开展束缚水饱和度建模X-X气田1井、3井、4井、8井均有岩心核磁实验,据此建立了孔隙度与岩心核磁束缚水饱和度模型。图 5为X-X气田孔隙度与核磁束缚水饱和度的关系图,两者相关性较好[6]。
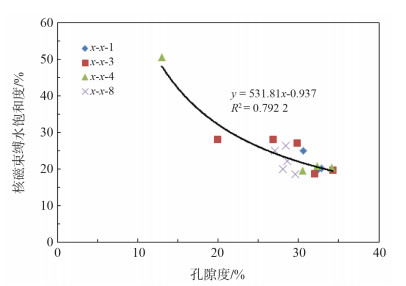 |
| 图 5 核磁实验孔隙度与束缚水饱和度关系 |
因此,X-X气田岩心核磁资料建立的束缚水饱和度模型为[7]:
| $ {{S}_{\text{wi}}}=531.81{{\phi }^{-0.937}} $ | (3) |
其中:Swi为利用岩心核磁实验资料建模计算的束缚水饱和度,%;ϕ为测井计算的有效孔隙度,%。
X-X气田1井黄流组进行了钻井取心,图 6a为钻井取心岩心压汞毛管压力曲线图,进汞饱和度与毛管压力的曲线形态趋势基本一致,进汞曲线平缓段较长,分选好,无需分类建模。为消除渗透率和孔隙度的影响,对多块岩心进行J函数处理。图 6b为X-X气田含水饱和度与J函数关系图。依据图 6得到J函数计算含水饱和度的公式为[8]:
 |
| 图 6 X-X气田黄流组含水饱和度Sw与J函数关系 |
| $ {{S}_{\text{w}}}=\sqrt[-2.717]{\frac{0.316\ 2H\left( {{\rho }_{\text{w}}}-{{\rho }_{\text{o}}} \right)\sqrt{\frac{K}{\varphi }}}{2162.1{{\sigma }_{\text{R}}}\text{cos}{{\theta }_{\text{R}}}}} $ | (4) |
式中:Sw为利用压汞实验J函数建模计算的含水饱和度,%;H为油藏高度,m;ρw、ρo分别为水、油的密度,g/cm3;K 为油层中各点的渗透率,mD;ϕ为油层中各点的孔隙度,%;σR为油气层界面张力,mN/m,一般气水界面张力取50 mN/m;θR为油气层接触角,°,一般气水界面接触角取0°。
4 模型效果分析根据前面研究,利用非电法饱和度模型计算含水饱和度,并建立核磁束缚水饱和度与孔隙度的关系。图 7为X-X-B井岩心核磁实验建模计算束缚水饱和度效果图,第十二道蓝色曲线是电法模型印尼公式计算的含水饱和度,粉红色曲线是岩心核磁实验建模计算的束缚水饱和度,在H_ ID气层段顶部束缚水饱和度与含水饱和度几乎重合,气层段底部由于受泥浆侵入影响,局部电阻率有一定程度降低,导致计算饱和度存在一定的差异。
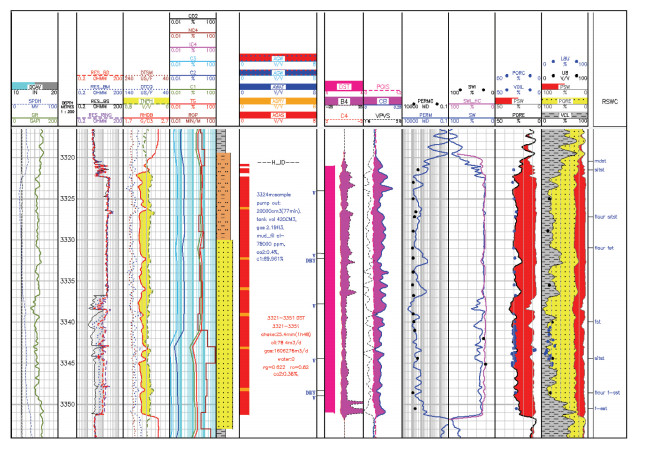 |
| 图 7 X-X-B井岩心核磁建模计算束缚水饱和度效果 |
图 8为X-X-B井压汞J函数计算束缚水饱和度的效果图,H_Ⅱ和H_Ⅳ气组打到气水界面,确定Ⅱ气组的自由水面为3 369 m(MD),Ⅳ气组的自由水面为3 475 m(MD)。第十二道蓝色曲线是印尼公式计算的含水饱和度,绿色曲线是岩心压汞J函数计算的束缚水饱和度,H_Ⅱ和H_Ⅲ两个气组印尼公式计算的含水饱和度与岩心压汞J函数计算的含水饱和度结果吻合,利用非电法毛管压力J函数计算油气层束缚水饱和度结果可靠。图 9为X-X气田岩心测量束缚水饱和度与测井建模计算束缚水饱和度结果对比图,如图所示,测井建模计算束缚水饱和度与岩心分析束缚水饱和度相关性较好,两者绝对误差控制在8%以内,说明X-X气田测井建模计算束缚水饱和度的方法有效。
 |
| 图 8 X-X-B井岩心压汞J函数计算含水饱和度效果 |
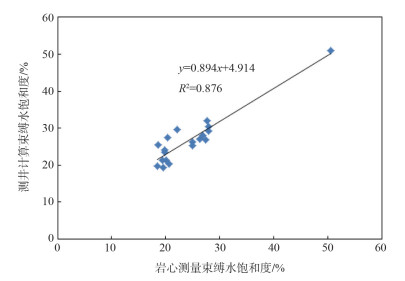 |
| 图 9 X-X气田岩心测量束缚水饱和度与测井建模计算束缚水饱和度结果对比 |
5 结论
通过岩心毛管压力实验分析表明,孔隙度大小一定的情况下,随着气柱高度增大,束缚水饱和度出现降低;烃柱高度一定的情况下,随着孔隙度增大,束缚水饱和度也呈下降趋势。底水气藏可采用J函数方法确定储层束缚水饱和度,也可利用岩心核磁资料建立核磁束缚水饱和度与孔隙度的模型来确定束缚水饱和度。结合岩心毛管压力资料以及电法计算含水饱和度的结果可确定束缚水饱和度模型计算结果可靠,为莺琼盆地X-X气田储层流体性质识别和定量评价、储量计算奠定坚实基础。
| [1] |
孙怡. 成藏动力对束缚水饱和度的影响[J]. 油气地质与采收率, 2007, 14(2): 64-66. DOI:10.3969/j.issn.1009-9603.2007.02.017 |
| [2] |
张效正. 用双电层理论说明粘土的粘结机理[J]. 江苏工学院学报, 1994, 15(2): 94-98. |
| [3] |
罗蛰潭, 王允诚. 油气储集层的孔隙结构[M]. 北京: 科学出版社, 1986.
|
| [4] |
李晓辉.复杂泥质砂岩储层束缚水饱和度计算方法研究[D].长春: 吉林大学, 2006. http://cdmd.cnki.com.cn/Article/CDMD-10183-2006109058.htm
|
| [5] |
高华, 高楚桥, 胡向阳. 莺歌海盆地束缚水饱和度影响因素研究[J]. 石油物探, 2005, 44(2): 158-159. DOI:10.3969/j.issn.1000-1441.2005.02.015 |
| [6] |
岳文正, 陶果, 赵克超. 用核磁共振及岩石物理实验求地层束缚水饱和度及平均孔隙半径[J]. 测井技术, 2002, 26(1): 22-25. DOI:10.3969/j.issn.1004-1338.2002.01.006 |
| [7] |
Coates G, 肖立志, Prammer M.核磁共振测井原理与应用[M].孟繁莹, 译.北京: 石油工业出版社, 2007.
|
| [8] |
何更生. 油层物理[M]. 北京: 石油工业出版社, 1994.
|
 2018, Vol. 38
2018, Vol. 38

