| WZ油田人工举升方式优选研究 |
WZ油田位于南海北部湾盆地西部涠西南低凸起西斜坡, 油气主要集中在古近系渐新统涠洲组涠三段和始新统流沙港组流二段, 储层主要为中孔中渗储层, 储层物性好, 属正常压力温度系统。原油为中-低密度、中-高含蜡量、低含硫的常规原油, 伴生气含少量CO2, 不含H2S。近些年在涠西区块的一系列勘探成果证实WZ油田地质储量丰富, 地层能量充足, 具有极大的商业开发价值。而在WZ油田开发方案设计过程中, 选择何种采油方式进行开发成为充分发挥油井产能、取得最佳经济效益的一项关键技术。
目前海上常用人工举升方式有电潜泵、螺杆泵、气举、水力活塞泵、水力射流泵等, 不同的举升方式有其各自的适用性和特点[1-10](表 1), 需根据具体的油藏条件、流体性质、生产状况等因素综合考虑优选举升方式, 才能最大限度挖掘油井产能, 实现合理高效开发。因此, 油井举升方式的优选是一个多指标的综合决策问题。目前, 针对多指标综合决策问题可采用的方法主要有模糊评价法、TOPSIS法[11-16]等。在这些方法之中, 模糊评价法理论相对成熟、可靠性高、操作性强, 现场应用较广。因此, 本文针对WZ油田特点, 应用系统层次模糊优选模型从工艺适应性角度优选了WZ油田人工举升方式, 为WZ油田采油工程方案设计提供了理论指导和技术支持。
| 表 1 海上常用人工举升方式优缺点 |
1 系统层次模糊优选模型
多指标方案评价优选问题具有模糊性和相对性, 针对这一问题衍生出模糊优选模型, 相比于传统模糊综合评判线性加权模型, 模糊优选模型计算出的各方案相对优属度具有更大的分散性, 更易于做出决策和选择。而系统层次模糊优选就是将系统层次分析与模糊优选理论相结合, 进而确定最优方案的一种多指标多层次综合评价方法。
1.1 单元系统模糊优选理论模型系统层次模糊优选模型是在单元系统模糊优选理论模型基础上建立起来的, 单元系统模糊优选理论模型计算步骤如下[17]:
(1) 建立指标特征值矩阵
设系统有q个决策组成的论域U, 其中有n个决策满足约束集形成决策集:
| $ D = \left\{ {{d_1}, {d_1}, \cdots, {d_{\rm{n}}}} \right\} $ |
设系统有m个指标组成对决策集D的评价指标集:
| $ p = \left\{ {{p_1}, {p_2}, \cdots, {p_{\rm{m}}}} \right\} $ |
依据m个指标对n个决策的评价, 可用指标特征值矩阵表示为:
| $ X = \left[{\begin{array}{*{20}{c}} {{x_{11}}}&{{x_{12}}}& \cdots &{{x_{1{\rm{n}}}}}\\ {{x_{21}}}&{{x_{22}}}& \cdots &{{x_{2{\rm{n}}}}}\\ \vdots&\vdots&\ddots&\vdots \\ {{x_{{\rm{m1}}}}}&{{x_{{\rm{m2}}}}}& \cdots &{{x_{{\rm{mn}}}}} \end{array}} \right] = {\left( {{x_{{\rm{ij}}}}} \right)_{{\rm{m}} \times {\rm{n}}}} $ | (1) |
式中:dj为第j个决策; pi为第i个评价指标; xij为决策j指标i的特征值, i=1, 2, …, m; j=1, 2, …, n。
这种由处在同一层次的m个指标共同作用而组成的系统称为多指标单元系统, 简称单元系统。
(2) 变换指标相对优属度矩阵
采用工程模糊集理论中指标相对优属度公式将指标特征值矩阵变换为指标相对优属度矩阵。
对越大越优型指标
| $ {r_{{\rm{ij}}}} = \frac{{{x_{{\rm{ij}}}}}}{{{ \vee _{\rm{j}}}{x_{{\rm{ij}}}}{ \wedge _{\rm{j}}}{x_{{\rm{ij}}}}}} $ | (2) |
对越小越优型指标
| $ {r_{{\rm{ij}}}} = 1 - \frac{{{x_{{\rm{ij}}}}}}{{{ \vee _{\rm{j}}}{x_{{\rm{ij}}}}{ \wedge _{\rm{j}}}{x_{{\rm{ij}}}}}} $ | (3) |
式中:rij rij为决策j评价指标i相对优属度; ∨、∧分别为取大取小运算符; ∨j xij、∧jxij分别为评价指标i的最大、最小特征值。
通过计算, 将指标特征值矩阵变换为指标相对优属度矩阵, 即:
| $ R = \left[{\begin{array}{*{20}{c}} {{r_{11}}}&{{r_{12}}}& \cdots &{{r_{1{\rm{n}}}}}\\ {{r_{21}}}&{{r_{22}}}& \cdots &{{r_{2{\rm{n}}}}}\\ \vdots&\vdots&\ddots&\vdots \\ {{r_{{\rm{m1}}}}}&{{r_{{\rm{m2}}}}}& \cdots &{{r_{{\rm{mn}}}}} \end{array}} \right] = {\left( {{r_{{\rm{ij}}}}} \right)_{{\rm{m}} \times {\rm{n}}}} $ | (4) |
(3) 选取优等决策与劣等决策
根据相对隶属函数定义和优选的相对性, 可把优等决策G和劣等决策B分别看作参考连续统中介过度的两极。优等决策应具有最大的相对优属度, 设
| $ G = {\left( {{g_1}, {g_2}, \cdots, {g_{\rm{m}}}} \right)^T} = {\left( {1, 1, \cdots, 1} \right)^T} $ | (5) |
劣等决策应具有最小相对优属度, 设
| $ B = {\left( {{b_1}, {b_2}, \cdots, {b_{\rm{m}}}} \right)^T} = {\left( {0, 0, \cdots, 0} \right)^T} $ | (6) |
也可采用
| $ \begin{array}{l} G = {\left( {{g_1}, {g_2}, \cdots, {g_{\rm{m}}}} \right)^T}\\ \;\;\; = {\left( {{r_{11}} \vee {r_{12}} \vee \cdots \vee {r_{1{\rm{n}}}}, {r_{21}} \vee {r_{22}} \vee \cdots \vee {r_{2n}}, \cdots, {r_{{\rm{m1}}}} \vee {r_{{\rm{m2}}}} \vee \cdots \vee {r_{{\rm{mn}}}}} \right)^T} \end{array} $ | (7) |
| $ \begin{array}{l} B = {\left( {{b_1}, {b_2}, \cdots, {b_{\rm{m}}}} \right)^T}\\ \;\;\; = {\left( {{r_{11}} \wedge {r_{12}} \wedge \cdots \wedge {r_{1{\rm{n}}}}, {r_{21}} \wedge {r_{22}} \wedge \cdots \wedge {r_{2n}}, \cdots, {r_{{\rm{m1}}}} \wedge {r_{{\rm{m2}}}} \wedge \cdots \wedge {r_{{\rm{mn}}}}} \right)^T} \end{array} $ | (8) |
式中:gi, bi分别为评价指标i优等取值和劣等取值; ∨、∧分别为取大取小运算符, i=1, 2, …, m。
(4) 计算指标权重
某一指标在整体中的相对重要程度称为该指标的权重, 是相对其他指标而言的。在总体评价中, 各评价指标所起的作用可以由权重的大小表示, 权重大, 说明该指标在整体评价中所占的分量重。权重分配是否合理准确对评价结果的准确性将产生直接影响。
指标权重常用的确定方法有层次分析法、专家评估法、模糊逆方程法、客观定权法等。相比较而言, 层次分析法计算简便、操作性强、可靠度高、现场应用广泛, 因此本文采用层次分析法计算各指标主观权重, 并结合基于指标方差和变异系数的权重模型来对主观权重进行修正, 提高评价结果可靠性, 这两种权重计算方法详见参考文献[17-18]。由此得到系统中m个指标的权重向量
| $ W = {\left( {{\omega _1}, {\omega _2}, \cdots, {\omega _{\rm{m}}}} \right)^T} $ | (9) |
式中:ω为指标i的权重, 且
(5) 确定最优决策
| $ {u_{\rm{j}}} = \frac{1}{{1 + {{\left\{ {\frac{{\sum\limits_{i = 1}^m {{{\left[{{\omega _{\rm{i}}}\left( {{g_{\rm{i}}}-{r_{{\rm{ij}}}}} \right)} \right]}^p}} }}{{\sum\limits_{i = 1}^m {{{\left[{{\omega _{\rm{i}}}\left( {{r_{\rm{i}}}-{b_{{\rm{ij}}}}} \right)} \right]}^p}} }}} \right\}}^{\frac{2}{p}}}}} $ | (10) |
当gi=1, bi=0, 则得到决策相对优属度模型为
| $ {u_{\rm{j}}} = \frac{1}{{1 + {{\left\{ {\frac{{\sum\limits_{i = 1}^m {{{\left[{{\omega _{\rm{i}}}\left( {1-{r_{{\rm{ij}}}}} \right)} \right]}^p}} }}{{\sum\limits_{i = 1}^m {{{\left( {{\omega _{\rm{i}}}{r_{{\rm{ij}}}}} \right)}^p}} }}} \right\}}^{\frac{2}{p}}}}} $ | (11) |
式中:uij为决策j对优的相对隶属度, i=1, 2, …, m; j=1, 2, …, n; p为距离参数, p=1时为海明距离, p=2时为欧氏距离。
在满足约束的决策集D中, 决策相对优属度最大的决策称为满意决策, 从大到小的排列次序为决策的满意排序。
1.2 系统层次模糊优选模型系统层次模糊优选是对单元系统优选模型的拓展。系统方案的优选由若干个评价因素或指标的特征值来描述。根据系统可分性原理, 将评价因素按其属性分解为若干个分系统。然后逐一对每个分系统进行方案集的模糊优选评价, 确定分系统中各个方案从属于“优”这个模糊概念的优属度。把低层次单元系统的输出作为高一级单元系统的输入, 根据各个分系统各方案的优属度进行高一层次的模糊优选评价。如此, 由系统的最低层次出发, 逐一的对每层进行模糊评价优选, 最后得出最高层次的优劣排序, 确定最终的优选方案。
2 WZ油田人工举升方式优选 2.1 建立适应性评价指标体系一种采油方式是否为最优的选择, 首先要看其从工艺上能否适应油田开发的需要, 如果满足不了, 也就没有进行下一步讨论的必要。因此, 先从举升方式工艺适应性角度出发优选WZ油田人工举升方式, 进而再决定是否通过经济评价对比确定最优采油方式。通过分析影响优选举升方式相关因素, 筛选出16项工艺适应性评价指标, 根据指标属性建立了两层的适应性评价指标体系。主指标层包括油井产液量、下泵深度、井下特征、油藏特性、设备特点5项内容, 在这5项主指标下分列14项子指标层评价因素, 得到适应性评价指标体系(图 1)。
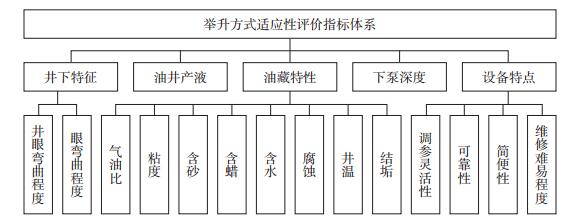 |
| 图 1 举升方式适应性评价指标体系 |
2.2 确定指标评价集
针对举升方式适应性评价指标不确定性和不可量化的特点, 本文采用等级法[19-20]对主指标及其相应的子指标适应性标值进行分级。根据各种人工举升方法工艺特点, 指标评语分为最强、强、适合、不强、不适合五个等级, 相应的等级数值分别为4、3、2、1、0, 评价指标分级结果见表 2。结合油井自喷期结束对应物性参数、产量数据等, 得到油井指标评价集, 这里以A1井为例, 说明具体计算过程(表 3)。
| 表 2 举升方式工艺适应性评价指标分级表 |
| 表 3 A1井指标评价集 |
2.3 计算指标权重
采用层次分析法计算主观权重, 采用权重模型法计算客观权重, 进而通过乘积加权[12]获得各评价指标综合权重:
| $ {W_{\rm{i}}} = \frac{{{w_i}{\omega _i}}}{{\sum\limits_{i = 1}^m {{w_i}{\omega _i}} }} $ | (12) |
式中:wi为主观权重; ωi为客观权重, i = 1, 2, …, m。权重计算结果见表 4。
| 表 4 A1井各评价指标综合权重 |
2.4 优选人工举升方式
由于指标评价值属于越大越优型, 因此采用式(2)对表 4指标评价集进行相对优属度计算, 见表 5。
| 表 5 A1井评价指标相对优属度 |
由表 5得到各子指标相对优属度矩阵, 即
井下特征子指标相对优属度矩阵:
| $ {R_1} = \left[{\begin{array}{*{20}{c}} {0.40}&{0.40}&{0.40}&{0.40}&{0.60}\\ {0.33}&{0.33}&{0.50}&{0.67}&{0.50} \end{array}} \right] $ |
油藏特性子指标相对优属度矩阵:
| $ {R_2} = \left[{\begin{array}{*{20}{c}} {0.33}&{0.67}&{0.67}&{0.33}&{0.33}\\ {0.43}&{0.57}&{0.43}&{0.43}&{0.43}\\ {0.50}&{0.67}&{0.67}&{0.50}&{0.33}\\ {0.50}&{0.67}&{0.33}&{0.50}&{0.50}\\ {0.67}&{0.67}&{0.33}&{0.67}&{0.67}\\ {0.67}&{0.67}&{0.33}&{0.67}&{0.67}\\ {0.57}&{0.43}&{0.57}&{0.57}&{0.57}\\ {0.75}&{0.75}&{0.25}&{0.50}&{0.50} \end{array}} \right] $ |
设备特点子指标相对优属度矩阵:
| $ {R_3} = \left[{\begin{array}{*{20}{c}} {0.33}&{0.33}&{0.67}&{0.50}&{0.50}\\ {0.75}&{0.50}&{0.75}&{0.25}&{0.50}\\ {0.60}&{0.60}&{0.40}&{0.60}&{0.40}\\ {0.33}&{0.33}&{0.67}&{0.50}&{0.50} \end{array}} \right] $ |
根据系统层次模糊优选理论, 取优等决策G和劣等决策B的因素gi=1, bi=0, 取p=1(海明距离), 则由式(11)得到决策相对优属度模型为
| $ {u_{\rm{j}}} = \frac{1}{{1 + {{\left\{ {\frac{{\sum\limits_{i = 1}^m {{\omega _{\rm{i}}}{r_{{\rm{ij}}}}} }}{{\sum\limits_{i = 1}^m {{\omega _{\rm{i}}}{r_{{\rm{ij}}}}} }}} \right\}}^2}}} $ | (13) |
结合各指标综合权重, 采用式(13)计算得到井下特征、油藏特性、设备特点指标评价各采油方式的相对优属度向量, 即
井下特征子指标评价相对优属度向量:
| $ {U_1} = \left( {0.27, 0.27, 0.37, 0.48, 0.63} \right) $ |
油藏特性子指标评价相对优属度向量:
| $ {U_2} = \left( {0.42, 0.76, 0.57, 0.40, 0.38} \right) $ |
设备特点子指标评价相对优属度向量:
| $ {U_3} = \left( {0.73, 0.44, 0.83, 0.24, 0.48} \right) $ |
进而得到主指标评价各采油方式相对优属度矩阵:
| $ R = \left[{\begin{array}{*{20}{c}} {1.00}&{0.00}&{1.00}&{1.00}&{0.75}\\ {1.00}&{0.00}&{1.00}&{1.00}&{0.33}\\ {0.27}&{0.27}&{0.37}&{0.48}&{0.63}\\ {0.42}&{0.76}&{0.57}&{0.40}&{0.38}\\ {0.73}&{0.44}&{0.83}&{0.24}&{0.48} \end{array}} \right] $ |
结合主指标综合权重, 应用式(13)计算得到各采油方式对于优的相对隶属度向量:
| $ U = \left( {0.995, 0.010, 0.991, 0.494, 0.570} \right) $ |
根据相对隶属度越大越优原则, 结合计算结果, 5种采油方式优选次序为电潜泵、气举、水力射流泵、水力活塞泵、螺杆泵。螺杆泵由于不适用于大产液量和中深度井, 最终得分最小, 最不适合; 水力活塞泵和水力射流泵主要由于其下泵深度的限制, 相对评分较低; 电潜泵相对优属度最大, 是最适合于WZ油田A1井的人工举升方式, 其次是气举。
为了验证评价结果的准确性, 研究中引入改进的TOPSIS法[21]来优选WZ油田人工举升方式, 计算各采油方式与理想解的“垂面”距离Pi, 得:
| $ P = {\left( {2.51, 1\;327.14, 4.81, 795.74, 665.26} \right)^T} $ |
根据“值越小, 方案越优”的判别原则, 5种采油方式优选次序为电潜泵、气举、水力射流泵、水力活塞泵、螺杆泵。这与模糊优选方法评出的结果相一致, 进一步验证了模糊优选方法的准确性。同时, 从评价结果中可以看出, 电潜泵和气举两种方式的相对隶属度相近, 电潜泵有优势但不明显, 因此, 研究中对这两种举升方式做了进一步的经济评价, 通过经济评价指标对比, 最终确定电潜泵为WZ油田最优人工举升方式。
3 结论与建议(1) 采用系统层次模糊优选模型优选电潜泵为WZ油田最优人工举升方式, 通过TOPSIS法的计算进一步验证了该方法的准确性。
(2) 计算结果表明, 采用模糊优选法对多指标多层次方案进行优选过程中, 在某些情况下评价结果会出现相近情况, 在这种情况下可考虑引入其他评价指标来综合对比优选。
(3) 本文中评价指标不可量化, 采用等级法确定评价指标值, 若评价指标可量化, 则可以考虑建立隶属函数来确定评价指标值, 提高评价结果计算精度。
| [1] |
吴怀志, 管虹翔, 何保生, 等. 大排量螺杆泵技术在海上稠油油田的应用[J]. 科学技术与工程, 2013, 13(05): 1289-1292. DOI:10.3969/j.issn.1671-1815.2013.05.035 |
| [2] |
于继飞, 吕孝明, 刘书杰, 等. 海上稠油举升工艺适用性分析[J]. 石化技术, 2015, 22(06): 245-246. DOI:10.3969/j.issn.1006-0235.2015.06.181 |
| [3] |
戴建辉. 油田井下螺杆泵常见故障分析及应对措施[J]. 化学工程与装备, 2011(07): 92-93+, 30. |
| [4] |
李岩. 水力射流泵的选型[J]. 油气田地面工程, 2011, 30(06): 32-33. DOI:10.3969/j.issn.1006-6896.2011.6.016 |
| [5] |
张晓宾, 鞠文龙. 水力射流泵系统在埕岛油田的应用[J]. 断块油气田, 2008, 15(02): 125-128. |
| [6] |
刘合, 郝忠献, 王连刚, 等. 人工举升技术现状与发展趋势[J]. 石油学报, 2015, 36(11): 1441-1448. DOI:10.7623/syxb201511014 |
| [7] |
刘乾义, 郭庆平. 井下水力活塞泵力平衡分析计算[J]. 石油矿场机械, 2012, 41(07): 52-54. DOI:10.3969/j.issn.1001-3482.2012.07.013 |
| [8] |
陈宪侃, 万仁溥, 周赤烽, 等. 国内水力活塞泵应用分析[J]. 石油钻采工艺, 2011, 33(05): 121-124. DOI:10.3969/j.issn.1000-7393.2011.05.032 |
| [9] |
姚亦华.海上油田潜油电泵生产系统优化设计与工况诊断[D].成都: 西南石油学院, 2002: 1.
|
| [10] |
李英东, 陈淑香, 孙权. 海洋人工举升常用工艺技术综述[J]. 中国石油和化工标准与质量, 2014, 34(12): 91. DOI:10.3969/j.issn.1673-4076.2014.12.084 |
| [11] |
刘杰.多属性决策理论在优选采油方式的应用研究[D].成都: 西南石油大学, 2012: 6-15.
|
| [12] |
潘新莲.机械采油方式的综合评价与决策模型研究[D].青岛: 中国石油大学(华东), 2011: 34-36.
|
| [13] |
谢宇新, 周宇鹏, 崔海清. 机械采油方式优选的模糊评价法[J]. 科学技术与工程, 2010, 10(34): 8528-8532. DOI:10.3969/j.issn.1671-1815.2010.34.040 |
| [14] |
于蓝.胜坨油田机械采油方式优选研究[D].青岛: 中国石油大学(华东), 2007: 21-26.
|
| [15] |
阳鑫军. 利用等级优化方法优选采油工艺方案[J]. 天然气勘探与开发, 2004, 27(03): 54-56+, 5. DOI:10.3969/j.issn.1673-3177.2004.03.013 |
| [16] |
邵争艳.机械采油方式优选综合评价研究[D].哈尔滨: 哈尔滨工程大学, 2004: 26-30.
|
| [17] |
李希灿. 模糊数学方法及应用[M]. 北京: 化学工业出版社, 2017: 101-102+, 119-125.
|
| [18] |
谢季坚, 刘承平. 模糊数学方法及其应用[M]. 4版. 武汉: 华中科技大学出版社, 2013: 143-181.
|
| [19] |
杨阳, 曹砚锋, 隋先富, 等. 基于等级加权法的海上机械采油方式优选方法[J]. 石油钻探技术, 2016, 44(01): 73-78. |
| [20] |
尹志红, 李大鹏, 巩艳芬, 等. 人工举升方式技术适应性组合评价[J]. 科学技术与工程, 2011, 11(08): 1884-1887. DOI:10.3969/j.issn.1671-1815.2011.08.054 |
| [21] |
华小义, 谭景信. 基于"垂面"距离的TOPSIS法-正交投影法[J]. 系统工程理论与实践, 2004, 24(01): 114-119. DOI:10.3321/j.issn:1000-6788.2004.01.020 |
 2018, Vol. 38
2018, Vol. 38

