| 基于多弹簧—空间梁有限元模型的海上热采管柱力学分析 |
注多元热流体热采技术是提高渤海稠油油田产量的有效方法[1-2],但多元热流体注入过程中存在温度高(250~300 ℃),压力大(15~20 MPa),单次作业时间长(30~40天)等特征;另外,受海上油田地质条件影响,油井曲率变化大;以上因素导致海上注多元热流体热采管柱工作环境比地面热采井要复杂的多,热采管柱更容易发生屈服失效、拉伸断裂等工程事故。
目前常用的井下管柱结构力学分析方法中,大多假设管柱轴线与井轴线保持一致,或假设管柱与井筒处于某一理想接触状态[3-6]。这种管柱结构几何形态的假设能够满足井身轨迹平滑、地层压力小、注热温度低等井况的热采管柱结构力学分析,但对于高温、高压、井身曲率变化复杂的海上热采井,这种假设会导致管柱结构几何形态与井下真实情况相差甚远,管柱结构力学分析结果误差大,无法为管柱结构安全评价、优化、扶正器等工具配置提供合理的支撑数据。
本文充分考虑海上热采管柱工作环境特点,提出了多弹簧—空间梁有限元分析方法,通过数值迭代确定热采管柱与井筒的合理接触状态,从而得到井下管柱较真实的几何形态。结合三维井身结构中热采管柱微单元矢量分析模型,能够有效提高海上热采管柱力学分析结果精度,为热采管柱结构优化,特别是扶正器等关键工具配置提供可靠的理论数据支持。
1 管柱结构微单元矢量力学模型受海上油田地质条件的影响,油气井井身轨迹的曲率与挠率变化大,与常规直井相比,井下管柱在承受轴向拉压的同时,也存在弯曲与扭转的耦合作用。由于直杆模型无法分析管柱结构的弯曲与扭转,为准确分析海上热采井管柱结构力学状态,需建立基于三维井眼轨迹的管柱力学分析模型。
1.1 管柱结构微单元几何形态描述基于三维井眼轨迹,选取井筒中任一点O处管柱微元段为分析对象,如图 1所示。假设在t时刻,O点处井眼轨迹的法平面为
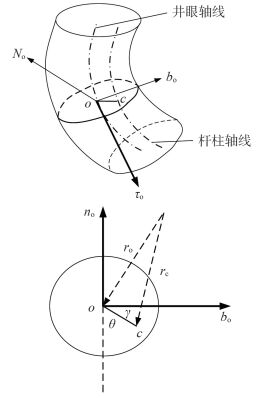 |
| 图 1 三维井眼轨迹中管柱几何形态 |
| ${{\vec r}_{\rm{c}}} = {{\vec r}_{\rm{o}}} + {{\vec r}_{{\rm{oc}}}} = {{\vec r}_{\rm{o}}} - r\cos \theta {{\vec n}_{\rm{o}}} + r\sin \theta {{\vec b}_{\rm{o}}}$ | (1) |
其中,
三维井眼轨迹中管柱的力学分析满足以下假设条件:(1)管材为各向同性;(2)管柱变形为线弹性;(3)管柱横截面为圆形;(4)变形前后管柱截面垂直于中性轴。
在管柱上截取弧长为ds的微元段,如图 2所示。
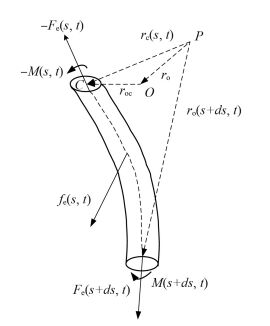 |
| 图 2 三维井眼轨迹中管柱结构微单元矢量力学模型 |
作用在微元体上的外力载荷:
| ${f_{\rm{e}}}\left( s \right) = \vec N + {{\vec q}_{\rm{e}}} + {{\vec f}_\lambda } + {{\vec f}_\mu } + {{\vec f}_{\rm{t}}} + {{\vec f}_{\rm{p}}}$ | (2) |
式中,
海上热采作业过程中,管柱下入过程中已随井眼曲率发生屈曲变形,管柱与井壁间的接触状态是非线性的,难以确定。因此常规的空间梁单元无法求解这类问题[7-8]。在常规空间梁单元模型基础上,引入轴向与径向弹簧元模型来处理管柱与井筒之间的接触,并提出弹簧接触判别准则,通过逐步迭代确定某一时刻井筒内管柱的几何形态,求解管柱与井筒之间的接触反力与摩擦力,从而分析管柱的力学参数。采用这种方法可实现空间梁对复杂曲率井眼中细长管柱的非线性接触分析,提高了管柱结构力学分析精度。
2.1 多弹簧—空间梁有限元模型一般意义上的有限单元法无法处理管柱与井壁的随机非线性接触问题,本文在对常规空间梁单元进行改进的基础上,建立了多弹簧—空间梁有限元模型,如图 3所示。采用空间梁单元模拟热采管柱,在每个梁单元节点上布置双向弹簧单元,通过弹簧元径向位移的分析判断管柱单元是否与井筒接触,并计算径向接触力,从而获得管柱接触位置的摩擦力。该方法的关键在于通过不断迭代逐步调整弹簧元的刚度,获得合理的管柱与井筒接触状态。
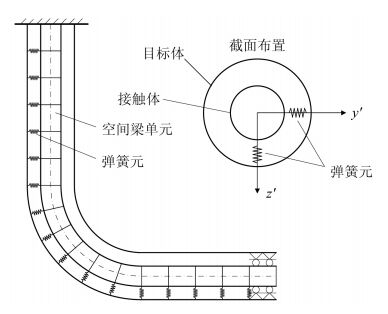 |
| 图 3 弹簧元—空间梁有限元模型 |
采用空间梁单元,将某一时刻井筒内的管柱自井口离散成n个单元,则生成n+1个梁单元节点。假设任意节点i处弹簧元的刚度分别为k'yi和k 'zi, 相对应空间梁单元在节点坐标系下的节点位移分别为v' i和w' i, 则该节点处产生的接触反力为:
| $\left\{ {\begin{array}{*{20}{l}} {{{F'}_{{\rm{yi}}}} = {{k''}_{{\rm{yi}}}} \cdot {{v'}_{\rm{i}}}}\\ {{{F'}_{{\rm{zi}}}} = {{k''}_{{\rm{zi}}}} \cdot {{w'}_{\rm{i}}}} \end{array}} \right.$ | (3) |
将节点接触反力写成矩阵的形式,并扩充为与梁单元节点位移维数相同的矩阵,可得:
| $\left\{ {{{F'}_i}} \right\} = \left[ {{{k'}_{\rm{i}}}} \right]\left\{ {{{u'}_{\rm{i}}}} \right\}$ | (4) |
其中:
| $\left. {\begin{array}{*{20}{l}} {\left\{ {{{F'}_i}} \right\} = {{\left[ {\begin{array}{*{20}{l}} 0&{{{F'}_{{\rm{yi}}}}}&{{{F'}_{{\rm{zi}}}}}&0&0&0 \end{array}} \right]}^{\rm{T}}}}\\ {\left[ {{{k'}_{\rm{i}}}} \right] = \left[ {\begin{array}{*{20}{l}} 0&0&0&0&0&0\\ 0&{{{k'}_{{\rm{yi}}}}}&0&0&0&0\\ 0&0&{{{z'}_{{\rm{yi}}}}}&0&0&0\\ 0&0&0&0&0&0\\ 0&0&0&0&0&0\\ 0&0&0&0&0&0 \end{array}} \right]}\\ {\left\{ {{{u'}_{\rm{i}}}} \right\} = {{\left[ {\begin{array}{*{20}{l}} 0&{{{v'}_{\rm{i}}}}&{w'}&0&0&0 \end{array}} \right]}^{\rm{T}}}} \end{array}} \right\}$ | (5) |
由于热采管柱与井筒的接触状态是未知的,需要通过节点径向位移计算结果进行判断。管柱与井壁接触的判别条件为:
| $\sqrt {{{v'}_{\rm{i}}} + {w'}_{\rm{i}}^2} > {d_{\rm{i}}}$ | (6) |
式中,di为热采管柱与井筒之间的环空间隙,m。
2.3 多弹簧—空间梁有限元整体平衡方程如图 3所示,相比空间梁有限元模型,本文建立的多弹簧—空间梁模型在y轴和z轴方向分别加一个弹性支承,相当于在y轴和z轴方向上加了反方向的弹性恢复力-kyivi和-kziwi。结合节点坐标系下空间梁单元的平衡方程建立方法[9](该理论较成熟,在此不赘述),拼装得到多弹簧—空间梁接触非线性问题求解的整体平衡方程式,见式(7)。
| $\left\{ {K' + {{K'}_{\rm{r}}}} \right\}\left\{ {u'} \right\} = \left\{ {p'} \right\}$ | (7) |
式中,K'为空间梁单元的整体刚度矩阵;K'r为弹簧的整体刚度矩阵;u'为梁单元节点位移矩阵;P'为载荷矩阵。
由于弹簧的刚度为未知量,因此式(7)需逐步迭代求解得到合理解,具体步骤为:
(1)首先假设管柱的初始位置与井轴线重合,即弹簧元初始刚度为0,通过式(7)求解得到梁单元每个节点的位移u'0;
(2)判断每个单元节点的位移u'0是否在合理范围内,即
(3)重新计算节点位移并调整弹簧的刚度;
(4)重复步骤(2)、(3),直到所有节点均满足
(5)提取节点坐标系下y轴与z轴方向的作用力即得到管柱接触力,进而得到管柱与井筒之间摩擦阻力。
3 管柱力学分析步骤根据有限元分析一般步骤,结合多弹簧—空间梁模型整体平衡方程求解方法,得到海上热采管柱力学分析具体步骤:
(1)确定t时刻管柱的下入深度,并根据井斜数据,采用空间梁单元划分管柱单元;
(2)建立3D井身结构中管柱微单元局部坐标系下的平衡方程;
(3)组装整体刚度矩阵,将管柱微单元局部坐标系下的力学平衡方程转换到整体坐标系;
(4)在空间梁单元的每个节点施加双向弹簧,并建立整体坐标系下弹簧刚度矩阵;
(5)将弹簧刚度矩阵添加到管柱整体刚度矩阵,建立多弹簧-空间梁有限元模型整体平衡方程,并求解;
(6)通过不断迭代,确定空间梁单元每个节点的合理弹簧刚度;
(7)求解整体平衡方程,获得热采管柱径向位移、接触力、摩擦力等力学参数。
4 算例分析以渤海油田某海上稠油井为例,采用多弹簧—空间梁有限元模型,分析了管柱下放到指定位置时的力学参数,为评价海上热采管柱安全提供了依据。
4.1 油井基础数据图 4所示为算例井的三维井身轨迹示意图。该井井深为1 776 m, 最大井斜角为91.89°,位于井深1 428.49 m处;油井狗腿度最大为8.04°/100ft;井口注汽压力为15.8 MPa, 注汽干度为70%,注汽温度为255 ℃,注汽段长度为214 m, 蒸汽粘滞系数为0.02,注气速度120 t/d, 热采管柱下入位置为井深1 770 m处。
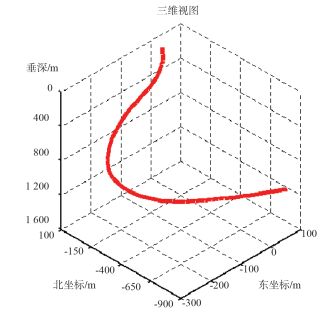 |
| 图 4 算例井三维井身轨迹 |
生产套管尺寸9"-5/8,钢级N-80,隔热油管尺寸4"-1/2,钢级N-80,顶深为1 470 m, 普通油管尺寸为2"-7/8,钢级为C-90,顶深为1 770 m。
4.2 热采管柱力学分析根据本文建立的热采管柱力学分析有限元模型,分析得到如图 5所示下放到指定位置时随井深变化的管柱径向位移分布。由图可得,热采管柱与井筒大部分处于接触状态;由于热采管柱采用了隔热油管与普通油管两种型号,受管柱尺寸的影响,在井深为1 470 m左右,曲线发生突变,与现场实际工况相符。
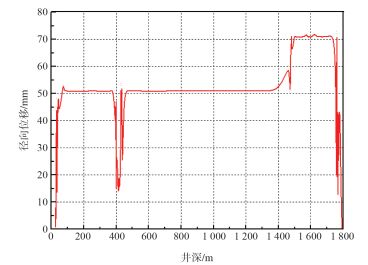 |
| 图 5 热采管柱径向位移分布 |
图 6所示为热采管柱摩阻随井深的变化规律。由图可得,受井身结构的影响,在井深为132 m位置管柱摩阻出现峰值1 992.9 N。根据图 6所示结果数据,可为热采管柱结构扶正器的配置提供理论依据。
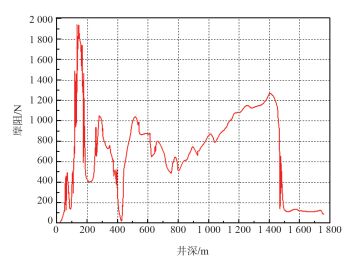 |
| 图 6 热采管柱摩阻分布 |
图 7所示为热采管柱轴力随井深的变化规律。由图可得,井口位置管柱轴力最大为328.5 N。管柱结构轴力是判断管柱结构屈曲变形的重要力学参数,因此根据图 7所示结果数据,可分析井筒内管柱结构是否发生螺旋屈曲变形,从而影响热采管柱的正常作业。
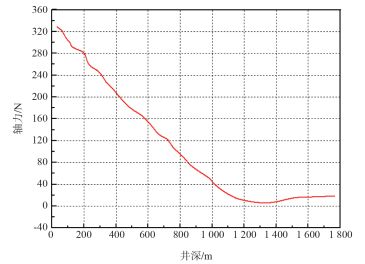 |
| 图 7 热采管柱轴力分布 |
图 8所示为热采管柱结构屈服安全系数随井深的分布。根据第四强度理论,在计算得到管柱结构Mises应力的基础上,结合管材屈服强度,得到图 8所示管柱结构的屈服安全系数分布规律。由图可得,管柱结构最小安全系数为4.3,远大于要求的最小安全系数1.5,因此在下放过程中,算例井不会发生管柱的屈曲破坏。在现场作业完成后起出管柱未发生破坏和变形。
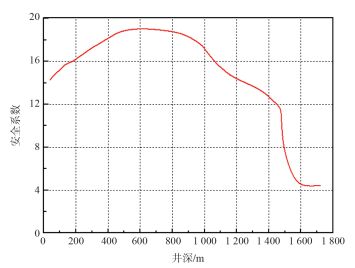 |
| 图 8 热采管柱结构屈服安全系数分布 |
5 结论
(1)提出了多弹簧—空间梁有限元模型,形成了复杂环境(井身曲率与挠率变化大、高温、高压)中海上热采管柱与井筒随机非线性动态接触的求解方法,采用此方法,能够较真实地反应井筒中管柱结构形态,提高了热采管柱力学分析结果精度。
(2)通过实例分析,验证了多弹簧—空间梁有限元模型求解海上热采管柱与井筒随机非线性接触问题的可行性,为较真实地描述复杂井身轨迹中管柱的受力与变形提供了一种有效方法,提高了海上热采管柱结构的力学分析精度,为管柱结构优化,特别是扶正器数量、位置等参数的设计提供合理的理论依据。
| [1] |
姜伟. 加拿大稠油开发技术现状及我国渤海稠油开发新技术应用思考[J].
中国海上油气,2006, 18 (2) : 123-125.
( 0) 0)
|
| [2] |
唐晓旭, 马跃, 孙永涛. 海上稠油多元热流体吞吐工艺研究及现场试验[J].
中国海上油气,2011, 23 (3) : 185-188.
( 0) 0)
|
| [3] |
高德利, 高宝奎. 水平井段管柱屈曲与摩阻分析[J].
石油大学学报(自然科学版),2000, 24 (2) : 1-3.
( 0) 0)
|
| [4] |
杜现飞, 王海文, 王帅, 等. 深井作业管柱下入能力研究[J].
燕山大学学报,2008, 32 (2) : 163-168.
( 0) 0)
|
| [5] |
Gao G H, Miska S. Dynamic Buckling and Snaking Motion of Rotating Drilling Pipe in a Horizontal Well[J].
SPE Journal,2010, 15 (3) : 867-877.
doi: 10.2118/113883-PA ( 0) 0)
|
| [6] |
Ritto T C, Soize C, Sampaio R. Non-Linear Dynamics of a Drill-String with Uncertain Model of the Bit-Rock Interaction[J].
International Journal of Non-Linear Mechanics,2009, 44 (8) : 865-876.
doi: 10.1016/j.ijnonlinmec.2009.06.003 ( 0) 0)
|
| [7] |
Omojuwa E O, Osisanya O, Ahmed R M. Integrated Dynamic Analysis for Optimal Axial Load and Torque Transfer in BHAs Used for Extended-Reach Horizontal wells[R]. SPE-161064-MS. Lexington, Kentucky, USA:SPE, 2012.
( 0) 0)
|
| [8] |
Omojuwa E O, Osisanya S, Ahmed R. Influence of Dynamic Drilling Parameters on Axial Load and Torque Transfer in Extended-Reach Horizontal Wells[R]. SPE-170672-MS. Amsterdam, The Netherlands:SPE, 2014.
( 0) 0)
|
| [9] |
邓学峰. 水平井完井管柱受力分析与摩阻预测方法[D]. 青岛: 中国石油大学(华东), 2009.
http://cdmd.cnki.com.cn/Article/CDMD-10425-2009221830.htm ( 0) 0)
|
 2017, Vol. 37
2017, Vol. 37

