| 井眼轨迹控制中过渡井段的研究 |
井眼轨迹控制在定向钻井的钻进过程中非常重要,尤其是定向钻进阶段和水平井钻井的水平井段。在钻井施工作业中,为了实现造斜,降斜或稳斜等工艺,在钻进过程中需要调整工具的造斜率,现场钻井过程中发现,调整后钻具未能马上按调整后的BHA的造斜特性(增斜,降斜或稳斜)进行钻进,而是会沿原井眼前进趋势继续钻进一段后,才能实现按调整后的造斜特性延伸。另外一种描述是指从一种井眼曲率变化到另一种井眼曲率时需一定长度的过渡井段。这种调整的滞后现象被称之为“井眼惯性” [1-2]。
过渡井段对井眼轨迹控制影响很重要,尤其是定向钻井和水平井钻井过程中的关键井段,在定向钻井中的造斜点,增斜结束点,降斜始点以及水平井的水平钻进阶段等需要精确控制井眼的轨迹的井段。特别是薄油层的水平井段,因靶体高度较小而使水平段轨迹控制难度大大增加,如不考虑过渡井段的影响,很有可能造成出靶。
1 过渡井段产生的原因分析BHA的结构决定了它的造斜特性,但是这是在钻进足够的长度之后所表现出来的力学特性。BHA是在特定的井眼中钻井的,不同井眼参数必然会对其产生影响,在井眼曲率需要改变的井段,BHA下入之前处于自由弯曲状态,下入井中之后弯曲变形受井眼的限制,BHA在钻头处产生较大的侧向力和一定的弯角,钻井过程中受侧向力的影响,钻头产生侧向位移,但是此时的侧向力所能产生的侧向位移与原来的BHA所产生的不同,也就造成井眼曲率不断发生变化,当侧向力不断趋近于零时,钻头就会按BHA设计结构的力学特性进行钻进。而在此过程阶段就会产生一个过渡段,此段井眼曲率不断变化,因此其长度也很难确定。
以上只是理论分析,现场实施过程中出现的问题也说明了这一点,比如井眼轨道为三段式的定向井钻井时,在造斜结束需要稳斜时,下入稳斜钻具后会增斜一段之后才会稳斜。图 1显示三个稳定器的稳斜钻具组合钻头侧向力随井眼曲率的变化[3]。
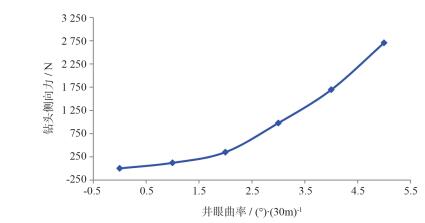 |
| 图 1 稳斜钻具组合钻头侧向力随井眼曲率的变化 |
由图可知,随着井眼曲率的增大钻头侧向力由近似为零增加到近2 700 N,即此稳斜组合在弯曲井眼中表现出略增斜的特性,但是侧向力增斜有限,因为其不足维持原井眼的曲率,以5°/30 m为例,钻成此井眼曲率的井眼需要单弯螺杆钻具,其侧向力大小为14 573.8 N,远大于此稳斜组合的钻头侧向力。所以随着不断钻进,井眼曲率逐渐变小至近似为零,此钻具组合开始发挥稳斜作用。
以上讨论的是井眼轨迹“由弯变直”的情况,井眼轨迹“由直变弯”时,以单弯双稳导向钻具组合为例。如图 2所示,此钻具组合的造斜力随着井眼曲率的变大急剧变小,说明在井眼延伸的过程中,井眼曲率的变化由强变弱,直至侧向力趋近于零时,井眼曲率不再变化,此钻具组合达到设计的造斜特性。
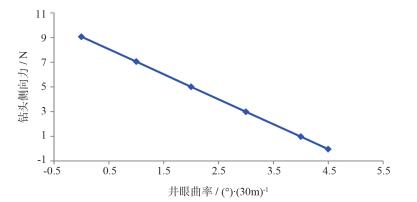 |
| 图 2 单弯双稳钻具组合钻头侧向力随井眼曲率的变化 |
2 过渡井段的计算 2.1 过渡井段长度的确定
无论井眼轨迹“由弯变直”还是“由直变弯”,分析BHA造斜特性的力学模型是一样的,所以过渡段的计算是相同的。管柱力学分析中认为BHA上部钻具与井眼下井壁相切,切点以上钻柱对BHA的力学特性影响不大[4],由此推论,过渡段的长度近似等于切点以下钻具的长度(如图 3所示),此切点长度可由加权余量或其它方法计算而得。值得注意的是,根据BHA造斜率的预测原理,钻头侧向力为零时计算的井眼曲率为设计的造斜率,此时切点长度才是过渡段的长度。
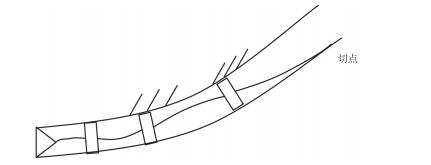 |
| 图 3 过渡井段示意图 |
2.2 过渡井段井斜角分析
过渡段的井眼曲率是变化的,由原井眼曲率经过过渡段后变为后下入的BHA的井眼曲率,井眼曲率连续变化,经过过渡段后的井斜角的推导过程如下。
如图 4所示,由于井眼曲率是连续变化,已知原井眼的井眼曲率K1和调整后的井眼曲率K2,可得出井眼曲率的变化率为:
| $ \Delta K = \frac{{{K_{\rm{2}}}-{K_{\rm{1}}}}}{L} $ | (1) |
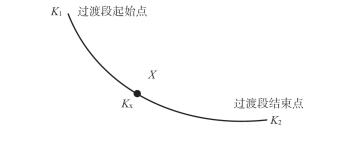 |
| 图 4 过渡井段井斜变化示意图 |
则任意弧长为s的X点处的井眼曲率为:
| $ {K_{\rm{X}}} = {K_{\rm{1}}} + \int_{\rm{0}}^s {\Delta Kds = } {K_{\rm{1}}} + \Delta K \cdot s $ | (2) |
单位长度变化的井斜角为:
| $ d\alpha = {K_{\rm{x}}}/30 \cdot ds $ | (3) |
那么过渡段结束点处的井斜角为
| $ {\alpha _{\rm{2}}} = {\alpha _{\rm{1}}} + ({K_{\rm{1}}}L + \frac{{\Delta K \times {L^{\rm{2}}}}}{{\rm{2}}})/30 $ | (4) |
式中:α1为过渡段起点的井斜角,(°);α2为过渡段末点的井斜角,(°);K1为原井眼的井眼曲率,(°) /30 m;ΔK为井眼曲率变化率,(°)/30 m2;K2为调整后的井眼曲率,(°)/30 m;L为过渡段的长度,m。
在定向井钻井施工过程中,需要精确控制井眼轨迹,在需要调整井眼曲率的情况下,就需要将过渡段对调整点的影响考虑在内,以免造成脱靶[5]。具体控制方法为计算出过渡段的长度,根据设计的调整点位置计算出实际中的调整点位置,然后按此点进行实际的钻井作业。
水平井钻井中,由于其井斜角趋近90°,水平井水平段井眼轨迹在铅垂面上是一条上、下起伏的曲线,钻头位置距离油层的上、下边界的距离是井眼轨迹控制的关键。为了保证钻头不出靶,需要对调整井段做出精确计算;变换导向方式后,要估算下一个调整点;应尽量减少调整次数,以提高机械钻速,降低钻进成本。
3 计算实例以水平井钻井水平井段的轨迹控制为例。在钻井过程中,要保证井眼在油层厚度之内,由于井眼轨迹过渡段的影响,很容易出靶,此时必须考虑井眼轨迹过渡段对调整点位置的影响。
如图 5所示,单弯双稳导向钻具各段长度分别为:L1=1.6,L2=3,L3=4,θ=1°,α1=80°,K1=0。由计算得工具造斜率为4.5°/30 m,过渡段长度L=16.9 m,K2=81.27 °。
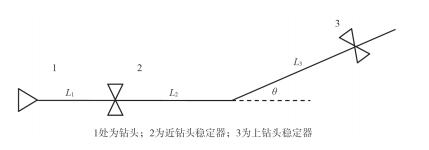 |
| 图 5 单弯双稳导向钻具组合结构图 |
若忽略过渡段的影响,直接按工具造斜率计算井斜角为82.54°。造成的结果是高估了钻具组合的造斜能力,井眼不按设计的轨道延伸,如果调整点距离油层边界过近,则有可能产生出靶的问题。为了保证钻具在极限的位置不出靶,则要在此调整点之前考虑造斜,即将调整点位置提前,由过渡段长度和工具的造斜率反算调整点的具体位置,确定之后,要估算下一个调整点位置,及时纠正井眼轨迹,确保钻具不出靶。
4 结束语根据钻井施工作业中遇到的问题,提出了井眼轨迹过渡段的概念,并根据底部钻具组合力学分析方法解释了过渡段出现的原因,并提出了过渡段长度和井斜角变化的计算方法。钻井作业中在需要调整井眼曲率的井段会出现过渡段,此段对于定向井钻井及水平井钻井的水平段井眼轨迹的控制有着重要影响,本文提出的方法可以指导钻井设计及施工中精确控制井眼轨迹的作业。
| [1] |
高德利, 刘希圣, 徐秉业.
井眼轨迹控制[M]. 北京: 石油工业出版社, 1994 : 34 -41.
( 0) 0)
|
| [2] |
毛建华, 王清江, 王治平, 等. "井眼惯性"对水平井水平段轨迹控制的影响探讨[J].
钻采工艺,2009, 32 (1) : 14-16.
( 0) 0)
|
| [3] |
蒋文震, 李群生, 王希勇, 等. 三稳定器钻具在定向井轨迹控制中的应用分析[J].
钻采工艺,2007, 30 (4) : 32-37.
( 0) 0)
|
| [4] |
白家祉, 苏义脑.
井斜控制理论与实践[M]. 北京: 石油工业出版社, 1990 : 44 -46.
( 0) 0)
|
| [5] |
刘修善. 实钻井眼轨迹的客观描述与计算[J].
石油学报,2007, 28 (5) : 128-132, 138.
( 0) 0)
|
 2017, Vol. 37
2017, Vol. 37

