| MRGC方法在储层分类及渗透率精细评价中的应用 |
随着勘探开发研究精细化的需求,测井计算渗透率与岩心分析渗透率在一个数量级误差范围内已不能满足生产需求。对于横向、纵向分布广、非均质性强,孔隙结构复杂的研究工区渗透率评价成为当前攻关的热点和难点。目前国内外最前沿的研究方法主要有孔渗参数法、孔喉结构参数法、R35孔喉半径法等方法进行渗透率分类研究。而这些方法主要基于经验公式或理论模型,对于渗透率一些主要影响参数很难通过测井手段直接得到[1-4]。研究表明划分不同的流动单元反映不同的孔喉特征,能解决孔隙结构复杂的问题,而流动带指标法FZI是唯一能定量划分流动单元的特征参数,并且能有效与测井曲线相结合,实际生产应用也比较方便[5]。因此,本文利用MRGC方法进行储层分类,并建立了不同流动单元渗透率模型,实现逐点连续划分流动单元,获取精细测井解释结果。
1 MRGC方法原理及优点 1.1 MRGC方法原理[6-7]采用向量空间模型,将优选的模型曲线和预测曲线转化为由若干个特征组成空间形式(t1,t2,…,tk),再将各个特征样本在曲线数据上赋予的数值填充到向量空间中。最终一个样本数据dj的数学表示形式为:wj(w1j,w2j,…,wkj,…,w|T|j),其中wkj表示特征tk在样本数据dj上的值,|T|表示特征向量的维数。
当样本数据表示为特征向量后,两个样本数据之间的相似程度可以通过空间中这两个向量的几何关系来度量。设有两个特征向量X=(x1,x2,…,x|T|) 和Y=(y1,y2,…,y|T|),则其相似度采用欧几里德距离来表示,如公式(1)所示:
| $ {\rm{sim}}\left( {X, Y} \right) = \frac{{\sum _{i = 1}^{\left| T \right|}{x_i}{y_i}}}{{\sqrt {\sum _{i = 1}^{\left| T \right|}{x_i}^2.} \sqrt {\sum _{i = 1}^{\left| T \right|}{y_i}^2} }} $ | (1) |
通过公式(1)可以计算待预测的特征向量与数据集中的所有特征向量的距离,利用高斯函数将距离转换为权重,根据距离的远近对预测结果进行贡献值补偿,再通过每个最近邻乘以相应权重,然后将所得到的结果累加,并除以所有权重值的和,如公式(2)所示:
| $ P = \sum _{i = 1}^k{S_i}.{w_i}/\sqrt {\sum _{i = 1}^k{w_j}} $ | (2) |
式中:P为最终的预测结果;Si为k个最近邻中的第i个;Wi为Si对应的权重值。
其算法核心原理是从学习样本数据体和待进行数值预测的新数据项中提取特征,将这些特征转换到向量空间,并将这两组数据进行集中比较,从中找出与待预测数据项最为接近的k个数据项,并对其求均值以得到最终的预测结果[8-10]。
1.2 MRGC方法优点MRGC方法是一种基于非参数K-近邻法和图形数据表示的多维点阵图形识别方法,可以用于分类回归预测。该方法主要靠周围有限的邻近的样本来确定所属类别,而不是靠判别类域的方法,因此对于类域的交叉或重叠较多的岩心物性和测井曲线样本集来说,MRGC方法较其他方法更为适合。
2 流动单元划分储层[3-5] 2.1 流动单元特征参数流动单元是指纵向上和横向上连续的储集带,同一流动单元内部具有相同的流体渗流特征,而流体微观渗流特性的主控因素受岩石物理特征和孔隙结构特征影响。为了更精确划分流动单元,依据渗流力学原理,引入扭曲因子τ、平均水动力半径Sgv、形状因子Fs,利用修正后的Kozeny-Carmen(柯兹尼-卡曼)方程(如公式(3))和平均流动半径为基础,对特征参数进行分析,识别表征不同流动单元。通过岩心物性资料,利用公式(4)~(6)计算可得到储层品质指数RQI、标准化孔隙度指标ϕZ、流动带指标FZI这三个能综合反映孔隙结构和地质特征的参数。
| $ \sqrt {\frac{K}{{{\phi _{\rm{e}}}}}} = \frac{{{\phi _{\rm{e}}}}}{{1-{\phi _{\rm{e}}}}} \times \frac{1}{{\sqrt {{F_{\rm{s}}}} \times \tau \times {S_{{\rm{gv}}}}}} $ | (3) |
| $ {\phi _{\rm{z}}} = \sqrt {\frac{K}{{{\phi _{\rm{e}}}}}} $ | (4) |
| $ {\phi _{\rm{z}}} = \frac{{{\phi _{\rm{e}}}}}{{1-{\phi _{\rm{e}}}}} $ | (5) |
| $ {\rm{FZI}} = \frac{{{\rm{RQI}}}}{{{\phi _{\rm{z}}}}} $ | (6) |
| $ {\rm{RQI = FZI}} \times {\phi _{\rm{z}}} $ | (7) |
式中:RQI为储层品质指数,μm;ϕZ为标准化孔隙度指标;FZI为流动带指标,μm;Fs为形状因子;Sgv为比表面。
2.2 流动单元划分储层将这三个特征参数曲线作为测井聚类分析数据库,利用MRGC方法对这些数据聚类分析,得到连续的测井相剖面。然后利用岩心分析的铸体薄片分析及粒度分析得到的岩石物理定名对测井相进行标定,使得相应的测井相具有地质特征的岩性相。从表 1中可以看出通过MRGC聚类分析方法得到的六类测井相岩性由砂砾岩→粉砂岩逐渐变细,物性变差与岩性具有非常好的对应关系;从图 1中可以看出六类测井相与测井曲线进行具有较明显的关联性,因此将储层划分为六类。
| 表 1 L油田流动单元物性、流动带指标参数 |
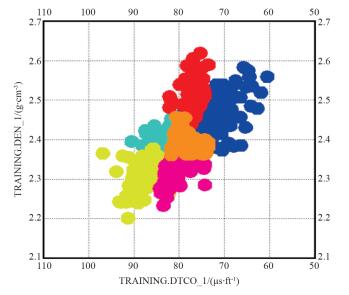 |
| 图 1 六类流动单元学习样本声波和密度交会图 |
为进一步得到储层划分的定量表征标准,依据流动单元划分原理,建立ϕZ和RQI双对数关系图(图 2),从图 2中可以看出相邻两类不同流动单元的岩心样品分布形态一致,并具有明显的区域差异,因此根据样品点的分布区域和形态可以确定相邻流动单元的分界线,并得到其表达式。结合公式(7)可以看出分界线斜率为FZI值,即通过每条分界线的斜率可以确定这六类FZI的临界值,而不同类型的储层,其FZI值不相同[8, 9, 11]。因此建立了以FZI值划分流动单元的分类标准,Ⅰ类:FZI>5.33,Ⅱ类:FZI在3.96~5.33,Ⅲ类:FZI在2.62~3.96,Ⅳ类:FZI在1.68~2.62,Ⅴ类:FZI在1.04~1.68,Ⅵ类:FZI<1.04,。流动单元划分标准及物性、流动带指标参数统计结果见表 1。
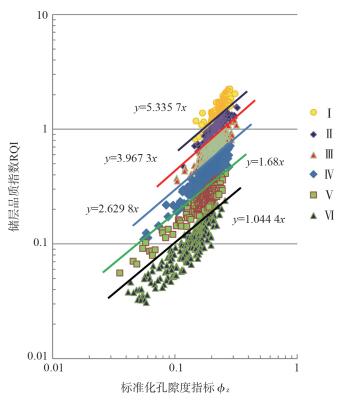 |
| 图 2 L油田流动单元划分标准图 |
3 建立分类渗透率模型
流动单元主要受储层矿物成分和孔隙结构控制,划分不同的流动单元可以反映不同的孔喉特征,而FZI值是唯一能定量划分流动单元的特征参数[12]。依据六类流动单元分类标准,对岩心样本数据进行分类统计,每一类储层的孔隙度与渗透率都具有较好的相关性,因此采用分划流动单元拟合建立了L油田六类储层渗透率计算模型模型(图 3)。六类覆压孔渗模型:Ⅰ类:y=5.919e0.223 1x;Ⅱ类:y=4.442 8e0.205 5x;Ⅲ类:y=2.460 7e0.198 7x;Ⅳ类:y=0.449 8e0.249 2x;Ⅴ类:y=0.128e0.277 5x;Ⅵ类:y=0.016 6e0.349 3x。
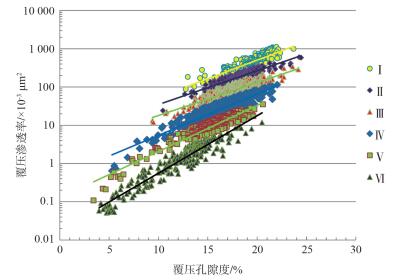 |
| 图 3 L油田不同流动单元覆压孔渗图 |
4 渗透率精细评价
首先,对研究区域测井曲线进行标准化后,对反应岩性、物性、电性的测井曲线进行相似性分析,优选了声波DTCO、伽马GR、密度RHOB为储层敏感曲线。然后,基于MRGC方法,利用优选的自然伽马、密度和声波这三条曲线作为模型样本输入曲线,岩心FZI值作为输出曲线,建立测井曲线与岩心FZI的预测模型。当输入其他未取心井的这三条模型曲线,通过建立的模型延展就可以计算得到一条FZI曲线。
通过模型输出的FZI曲线,结合建立的FZI分类标准的孔渗模型,就可以针对不同FZI值选择相应的模型计算得到逐点的渗透率(图 4)。图中第一道、第三道为优选的学习样本曲线道、第四道为孔隙度道、第五道为模型延展输出的FZI曲线道,第六道红色曲线为流动单元方法计算渗透率FZI_K、蓝色曲线为区域孔渗公式计算的渗透率PERM。
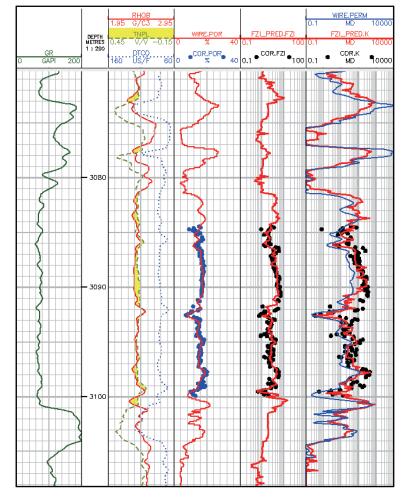 |
| 图 4 M井渗透率精细评价成果图 |
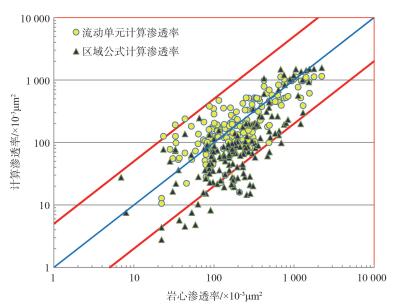
通过误差对比分析,图 5中横坐标是岩心渗透率,纵坐标是FZI计算渗透率,两条红线区域表示半个数量级误差范围,黄色圆点是FZI计算的渗透率,黑色点为区域公式计算的渗透率。从图 5可以看出,划分流动单元方法计算的渗透率与岩心分析渗透率大小整体一致,且集中在中线附近,而区域回归公式计算的渗透率较岩心分析渗透率明显偏小,相对黄色数据点较偏离中线。误差分析表明通过FZI计算的渗透率与岩心渗透率误差主要集中在半个数量级以内,明显提高了渗透率的评价精度,满足勘探开发精细评价的需要。
 |
| 图 5 M井两种方法计算的渗透率与岩心渗透率对比图 |
5 结论
(1)利用ϕZ和RQI双对数关系图确定不同流动单元的分界线,通过公式推导ϕZ和RQI关系来确定FZI是分界线的斜率,根据不同流动单元FZI的临界值,对研究区有效的进行划分储层类型。
(2)基于MRGC方法可以有效地将常规测井曲线与岩心实验数据结合起来,对非取心段进行曲线预测,且预测精度高。
(3)本文采用划分流动元和曲线预测技术相结合的方法进行渗透率精细评价,在实际应用中可操作性强,精度高,为储层评价提供了一种可靠的渗透率精细计算方法。
| [1] |
刘吉余. 流动单元研究进展[J].
地球科学进展,2000, 15 (3) : 303-306.
( 0) 0)
|
| [2] |
袁彩萍, 姚光庆, 徐思煌, 等. 油气储层流动单元研究综述[J].
地质科技情报,2006, 25 (4) : 21-26.
( 0) 0)
|
| [3] |
SOTO B R, GARCIA J C, TORRES F, et al. Permeability Prediction Using Hydraulic Flow Units and Hybrid Soft Computing Systems[R]. SPE 71455, 2001.
( 0) 0)
|
| [4] |
UGURU C I, ONYEAGORO U O, LIN J, et al. Permeability Prediction Using Genetic Unit Averages of Flow Zone Indicators (FZIs) and Neural Networks[R]. SPE 98828, 2005.
( 0) 0)
|
| [5] |
LEE S H, KHARGHORIA A, DATTA-GUPTA A. Electrofacies Characterization and Permeability Predictions in Complex Reservoirs[J].
SPE Reservoir Evaluation & Engineering,2002, 5 (3) : 237-248.
( 0) 0)
|
| [6] |
冯克鹏. KNN价格预测模型的研究与改进[J].
软件导刊,2010, 9 (10) : 84-86.
( 0) 0)
|
| [7] |
张孝飞, 黄河燕. 一种采用聚类技术改进的KNN文本分类方法[J].
模式识别与人工智能,2009, 22 (6) : 936-940.
( 0) 0)
|
| [8] |
王月莲, 宋新民. 按流动单元建立测井储集层解释模型[J].
石油勘探与开发,2006, 29 (3) : 53-55.
( 0) 0)
|
| [9] |
李阳. 储层流动单元模式及剩余油分布规律[J].
石油学报,2003, 24 (3) : 52-55.
( 0) 0)
|
| [10] |
YE S J, RABILLER P. A New Tool for Electro-facies Analysis : Multi-resolution Graph-based Clustering//SPWLA 41st Annual Logging Symposium[C]. Dallas, Texas : SPWLA, 2000 : 1-14.
( 0) 0)
|
| [11] |
张丽艳. 砂砾岩储层孔隙度和渗透率预测方法[J].
测井技术,2005, 29 (3) : 212-215.
( 0) 0)
|
| [12] |
王志章, 何刚. 储层流动单元划分方法与应用[J].
天然气地球科学,2010, 21 (3) : 362-366.
( 0) 0)
|
 2017, Vol. 37
2017, Vol. 37

