| 基于曲波变换的地震随机噪声压制新方法 |
噪声压制是地震勘探数据处理的主要任务之一。根据噪声与有效信号的相干性可将其分为随机噪声和相干噪声,本文主要针对随机噪声进行压制。曲波变换是目前备受关注的去噪方法之一,该方法由Candes和Donoho于1999年以一个数学概念提出,2004年首次被地球物理学家引入到地震数据去噪[1-3]。曲波变换对二阶可导函数具有最优逼近阶,且具有多方向、多尺度和各向异性的特点,这使得该变换很适合结构有很强几何性、正则性并表现为二阶可导曲线特征的地震信号;另外,曲波变换对地震数据的表达具有稀疏性,即用极少的曲波系数就可以表示原信号中的有效信号。本文在前人工作的基础上,通过对曲波域内的曲波系数结构及分布进行深入研究,发现有效信号的曲波系数仍具有地震同相轴特征,据此提出了一种新的噪声压制方法。
1 方法原理 1.1 曲波变换基本原理曲波变换的定义是将均方可积函数f映射为系数序列c (j, l, k) 的变换,其中j表示尺度参数,l表示方向参数,k表示位置参数。在快速离散曲波变换中,对于尺度为j,空间位置为b=(k1 · 2-j, k2· 2-[j/2]),直角坐标下的曲波函数为:
| $ {\phi _{j,l,k}} = {2^{3j/4}}{\phi _j}\left[ {S_{\theta i}^T\left( {x - x_k^{\left( {j,l} \right)}} \right)} \right] $ | (1) |
式中:θl为方位角;ϕj为曲波基函数;xk(j, l)=Sθi-Tb;Sθ为剪切矩阵;
曲波变换最核心的关系是曲波基的支撑区间满足:width ∝ length2,该关系称为各向异性尺度关系,它表明了曲波是一种具有方向性的基原子,这也是曲波变换具有很好的非线性逼近能力的根本原因。通过信号与某一曲波函数内积的形式能实现对信号的稀疏表达[4-8]:
| $ c\left( {j,l,k} \right) = < f,{\phi _{j,l,k}} > $ | (2) |
利用曲波的稀疏性,我们可将地震数据中随机噪声的衰减表述为如下的约束优化问题[9]:
| $ {P_\varepsilon }:\left\{ {_{\tilde f = A\tilde x}^{\tilde x = \arg {{\min }_{\rm{X}}}{{\left\| x \right\|}_1} = \sum _{i = 1}^N\left| {{x_i}} \right|st.{{\left\| {Ax - y} \right\|}_2} \le \varepsilon }} \right. $ | (3) |
式中:y为带有噪声的地震数据;A=CT表示反曲波变换;x表示曲波系数;ε为一任意小量;
由于该问题的求解较困难,用如下优化问题代替了上述约束优化问题:
| $ {P_{\rm{\lambda }}}:\left\{ {_{_{{{\tilde f}_{\rm{\lambda }}} = A{{\tilde x}_{\rm{\lambda }}}}^{}}^{\tilde x = \arg {{\min }_{\rm{X}}}\left[\kern-0.15em\left[ {y - Ax} \right]\kern-0.15em\right]_2^2 + \lambda {{\left[\kern-0.15em\left[ x \right]\kern-0.15em\right]}_1}}} \right. $ | (4) |
这里加入了一个起到正则化作用的阈值算子λ。问题Pλ是通过迭代阈值的方法求解的。其迭代序列为:
| $ x = {T_{\rm{\lambda }}}\left[ {x + {A^T}\left( {y - Ax} \right)} \right] $ | (5) |
将含噪的地震数据做曲波变换,得到各尺度各方向上的曲波系数,发现曲波系数在曲波域各区块的分布仍具有与地震信号相似的同相轴特征,即地震信号部分的曲波系数仍呈地震信号特征,而随机噪声部分的曲波系数的分布仍是随机的,基于此特征我们提出了将各个区块内的曲波系数作为处理目标的去噪新方法,即对各区块内曲波系数分别进行曲波变换并施以阈值,以此实现对曲波系数的“去噪”。
根据曲波变换原理,若f为含噪地震信号,进行一次曲波去噪可得到去噪结果f':
| $ f' = \sum c'\left( {j,l,k} \right).{\phi '_{j,l,k}} $ | (6) |
式中:c' (j, l, k) 为在曲波域经过处理的曲波系数;ϕ' j, l, k为反曲波函数。
由(6)式有,新方法去噪的结果f"可表示为:
| $ f'' = \sum c'''\left( {j,l,k} \right).{\phi '_{j,l,k}} $ | (7) |
式中:
| $ c''\left( {j,l,k} \right) = \left[ {c'\left( {j,l,k} \right),{\phi _{j,l,k}}} \right] $ | (8) |
所以有
| $ c'''\left( {j,l,k} \right) = \left[ {c''\left( {j,l,k} \right),{\phi _{j,l,k}}} \right] $ | (9) |
将式(6)、式(8)、式(9)代入式(7)得新方法去噪结果:
| $ f'' = \sum \left[ {\sum c'\left( {j,l,k} \right).{{\phi '}_{j,l,k}}.{\phi _{j,l,k}}} \right].{\phi '_{j,l,k}} $ | (10) |
该方法的核心步骤是将一次曲波变换的系数分解到不同尺度方向的小块区域,然后分别对这些区域系数再进行曲波变换。分解时的尺度数和方向数由被分解数据大小决定,图 1a中地震记录水平采样点为256个,故最合适的尺度数为5,基础方向数为8。经计算第一尺度和最高尺度的方向数均为1,第二、三尺度方向数为8,第四尺度方向数为16。曲波域内系数分布情况如图 1b所示。
 |
| 图 1 地震数据所对应曲波系数在曲波域内分布 |
新方法的实现如下:
对于一地震信号s,设有效信号为d,n为随机噪声,则去噪模型可表示为:
| $ s = d + n $ | (11) |
(1)根据数据大小确定尺度数和方向数,对s进行曲波变换,对得到的曲波系数c(j, l, k) 加阈值,再做反曲波变换,得去噪结果s';
(2)对s'进行曲波变换,将得到的曲波系数分解到各尺度各方向,把每一块曲波系数作为新的去噪对象;
(3)根据每个小块曲波系数的分布情况确定第二次曲波变换的尺度数和方向数,分别对每一块曲波系数进行曲波变换,得到二次变换后的曲波系数c"(j, l, k);
(4)对c"(j, l, k) 进行阈值处理,并进行反曲波变换,得到每一块的去噪后的曲波系数,将这些曲波系数合成为新的
(5)对
为了验证新方法的正确性和有效性,首先在合成的共炮点道集数据上做数值实验。速度模型为陡倾构造模型,如图 2a所示。水平网格点数为3 375,网格间隔为10,深度网格点数为570,网格间隔为10;记录共256道,道间距为50 m,时间采样点数为1 025,采样间隔为0.001 ms。共炮点道集如图 2b所示。加入幅值与有效信号最大值在一个数量级上的范围在-0.1~0.1之间的随机噪声,得到含噪剖面(图 2c),PSNR=50.32 dB。这里用PSNR(峰值信噪比)来衡量去噪水平。其计算公式为:
| $ {\rm{PSNR = 10}}\;{\log _{10}}\left( {{{\max }^2}/{\rm{MSE}}} \right) $ | (12) |
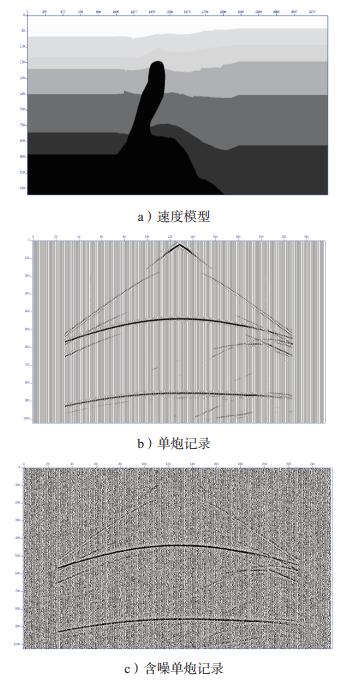 |
| 图 2 合成数据实验 |
式中:max为数据的峰值;MSE为原数据与处理数据之间的均方误差。
曲波变换去噪的结果如图 3a所示,新方法得到的去噪结果如图 3b所示。为方便对比去噪的效果,分别将原始数据、含噪数据、曲波变换去噪结果和新方法去噪结果的剖面取出相同位置的一部分进行放大,如图 3c、3d、3e、3f所示。计算得常规曲波变换去噪结果,PSNR=55.992 dB,新方法去噪结果,PSNR=61.164 dB。从图 3中可看出,新方法的去噪结果在较好地保存了地震波同向轴的同时,进一步去掉了噪声,其结果优于曲波变换的去噪结果。
 |
| 图 3 新方法去噪结果与常规曲波变换去噪结果对比 |
图 4可见,经处理的曲波系数得到了明显改善,对应有效信号的曲波系数留了下来,曲波系数的稀疏性增强。用这些新的曲波系数组合起来进行反曲波变换得到的结果,噪声必然会受到抑制,因此达到了改进去噪效果的目的。
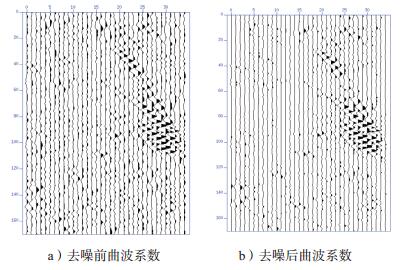 |
| 图 4 第三尺度、第三方向的曲波系数去噪前后对比情况 |
2.2 对比实验
为了验证本文提出的新方法(即用曲波变换处理曲波系数)的优越性,进行了与用小波变换和离散余弦变换处理曲波系数的对比实验。其结果如图 5和表 1所示。
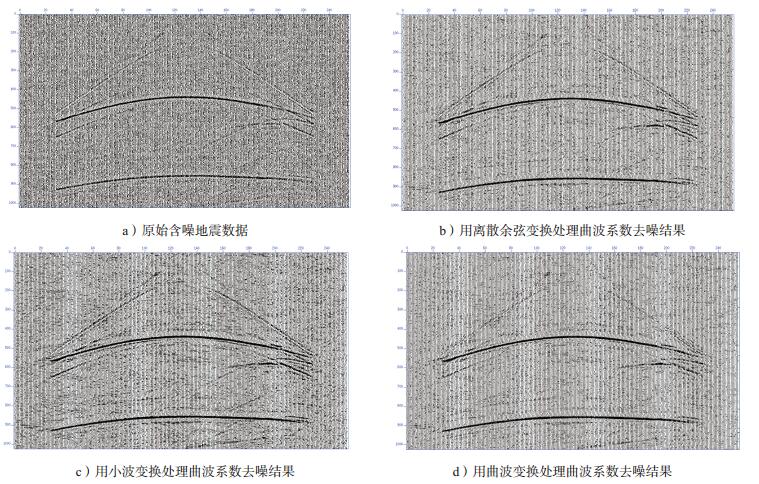 |
| 图 5 不同方法处理曲波系数去噪结果 |
| 表 1 不同方法处理曲波系数去噪结果量化对比 |
由图 5和表 1可知,三种方法对随机噪声都起到一定的压制,且均方误差都较小,其中曲波变换得到的结果均方误差最小,信噪比最高;从去掉噪声多少的角度看,小波变换和曲波变换所得结果优于离散余弦变换,但从有效信号的形态上讲,用离散余弦变换和曲波变换的处理结果要优于小波变换,前两者更好地保留了有效信号的信息,三者相比,后者在有效信号形态上失真程度最高。综合以上因素曲波变换处理结果最优。
3 结论本文利用了曲波变换的多尺度多方向性,及其对地震信号稀疏表达的特性,通过对曲波系数分布规律的研究,发现有效信号在曲波域内的系数也具有同相轴特征。基于现有的曲波变换去噪方法提出了以曲波系数为去噪目标的新方法,该方法是对传统方法的改进。经实验证明新方法正确且有效。与传统曲波变换去噪结果对比显示,该方法在提高信噪比上有显著作用;另外,通过与小波变换和离散余弦变换的对比实验表明曲波变换无论是对信噪比的提高还是对有效信号的保留都优于二者,印证了曲波变换对地震信号的最佳适应性,从而证明本文的方法在地震数据处理中具有一定价值。
| [1] |
胡天跃. 地震资料叠前去噪技术的现状与未来[J].
地球物理学进展,2002, 17 (2) : 218-223.
( 0) 0)
|
| [2] |
CANDÈS E J, DONOHO D L. Curvelets-a Surprisingly Effective Nonadaptive Representation for Objects with Edges[R]. Technical Report. Stanford : Department of Statistics, Stanford University, 1999.
( 0) 0)
|
| [3] |
MA J W, PLONKA G. A Review of Curvelets and Recent Applications[J].
IEEE Signal Processing Magazine,2010, 27 (2) : 118-133.
doi: 10.1109/MSP.2009.935453 ( 0) 0)
|
| [4] |
包乾宗, 陈文超, 高静怀. 基于第二代Curvelet变换的地震资料随机噪声衰减[J].
煤田地质与勘探,2010, 38 (1) : 66-70.
( 0) 0)
|
| [5] |
仝中飞. Curvelet阈值迭代法在地震数据去噪和插值中的应用研究[D]. 长春: 吉林大学, 2009.
( 0) 0)
|
| [6] |
韩佳君. Curvelet变换组合法压制地震随机噪声研究[D]. 长春: 吉林大学, 2010.
( 0) 0)
|
| [7] |
薛念. 基于Curvelet变换的地震数据插值和去噪[D]. 成都: 西南交通大学, 2010.
( 0) 0)
|
| [8] |
吴爱弟, 赵秀玲. 基于曲波变换的地震信号去噪方法[J].
中国石油大学学报 (自然科学版),2010, 34 (3) : 30-33.
( 0) 0)
|
| [9] |
WANG D L, TONG Z F, TANG C, et al. An Iterative Curvelet Thresholding Algorithm for Seismic Random Noise Attenuation[J].
Applied Geophysics,2010, 7 (4) : 315-324.
doi: 10.1007/s11770-010-0259-8 ( 0) 0)
|
 2017, Vol. 37
2017, Vol. 37

