| 高精度剩余速度分析研究 |
地震勘探在油气勘探中起着举足轻重的作用,它通过研究弹性波在地下的传播来研究地壳的地质结构[1]。多次叠加技术出现在上世纪60 年代,是地震数据处理中的必要环节。速度是地震勘探的重要参数,专业技术人员非常重视对速度的研究,速度分析的主要目的是为叠加、偏移归位等处理提供准确的速度参数。
速度对地震数据处理解释都起着很大的作用,因此人们为了获得该参数采用了许多方法,叠加速度分析就是其中之一,利用该方法得到叠加速度谱并拾取比较准确的速度,通过叠加速度还可以计算层速度,为地层对比、岩性识别、油气检测提供资料和新途径[2-3]。在国内郭树祥、付强等人提出了各种优化的速度分析方法[4-5],效果也不错。本文采用高精度剩余速度分析也是叠加速度分析的一种,该方法能够提高速度分析的精度。
1 理论基础剩余速度分析首先要进行常规的速度分析,然后通过剩余时差公式扫描更加精确的叠加速度 [6-8]。各向同性地层是一理论模型,在同层介质中假设地震波传播速度会跟随传播方向的改变而变化。各向同性地层在零偏移距时间t,偏移距x为样点处的剩余时差公式如下:
| $\tau \left( t,x \right)={{x}^{2}}\left( {{V}^{-2}}-Vre{{f}^{-2}} \right)/2t$ | (1) |
式中:τ 为剩余时差,t 为自激自收时间,V 为实际速度,Vref 为参考速度,x 为偏移距。
针对地震数据的一个CDP(共深度点道集),首先利用Vref 进行常规动校正,由以上公式可知参考速度与真实速度的差异将导致产生剩余时差,通过公式(1)扫描剩余时差并进行叠加处理[9-10],最后根据叠加效果求得更准确的叠加速度V。
2 剩余速度分析方法研究与实现利用剩余速度分析处理模型数据与实际数据并进行对比分析。
2.1 理论模型试验通过地震软件SU 合成了三层模型地震记录,并对它进行了剩余速度分析。正演模型参数见表 1。
| 表 1 三层模型参数 |
利用Dix 公式求得准确的均方根速度:
V1 = 1 508 m/s,V2 = 1 740 m/s。下面对一个满覆盖的CDP 进行处理,结果如图 1。
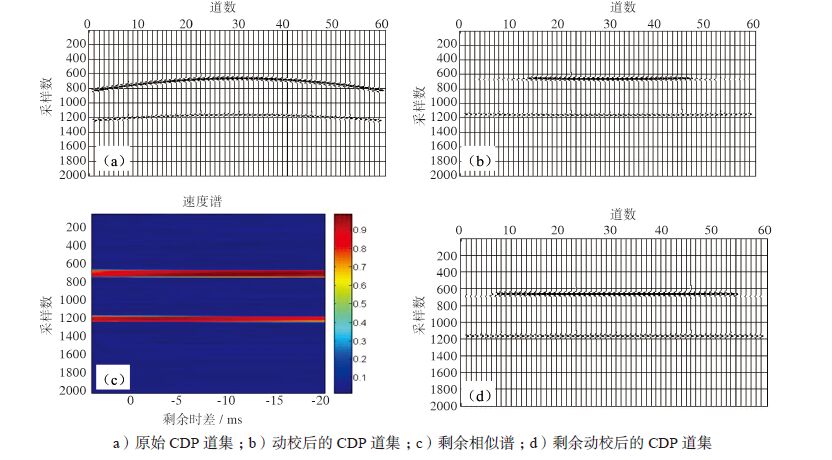 |
| 图 1 理论模型的剩余速度分析 |
图 1a 为一原始CDP 道集,地震反射波同相轴成双曲线形,第一个反射界面位于680 采样点附近,第二个反射界面位于1 170 采样点附近。图 1b 是利用参考速度进行传统动校正的结果,由于参考速度低于模型真实速度,动校过大。图 1c 是采用剩余时差(-20~4 ms)进行速度扫描绘制的相似谱,通过最大的相似能量值对应的时差求取叠加速度,并与理论均方根速度相比较:第一层1 515 m/s,绝对误差1 515 -1 508 = 7 m/s,第二层1 776 m/s,绝对误差1 776 -1 740 = 36 m/s,可见浅层分辨率比深层的高。图 1d 是利用剩余速度分析得到的叠加速度再次进行动校正的结果,可见同向轴基本校平,效果明显改善。
2.2 实际数据试验我们优选了一套实际数据进行试验,实际数据见表 2。
| 表 2 实际数据 |
图 2a、图 2b 中可见,经传统动校正后,同相轴基本拉平了,但是还有一些时移量,需要进行剩余速度分析,得到更加精确的速度。经过剩余速度分析产生速度谱(图 2c),可见剩余时差主要集中在负时差范围,可以看出参考速度比实际的速度低,通过相关值提取精确的叠加速度。图 2d为利用新提取的叠加速度校正的结果,同相轴校平效果明显改善。
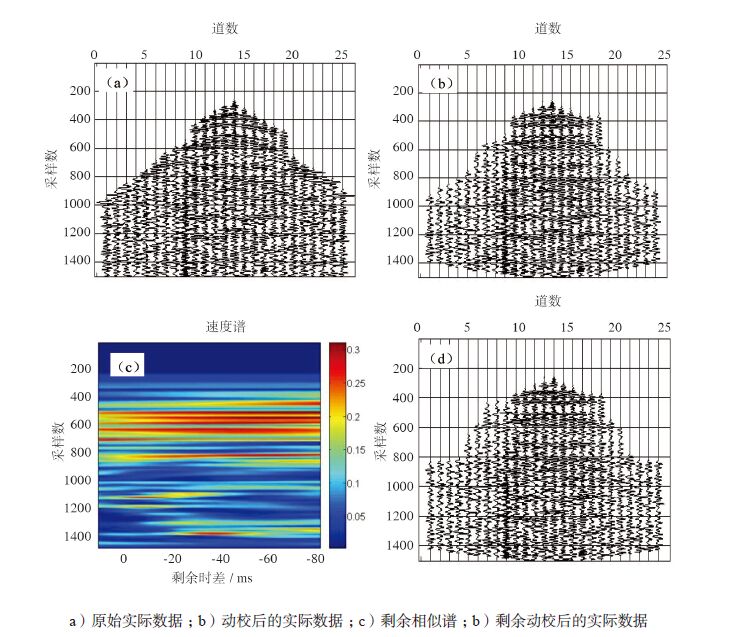 |
| 图 2 实际数据的剩余动校正 |
2.3 局部回归法三维插值研究
剩余速度分析首先扫描一个CDP 地震数据,并对整个CDP 数据进行处理,处理速度比常规速度分析快,但是由于地震数据的分辨率、噪音等影响,自动拾取速度会导致各CDP 之间产生不合理的不连续性,这样就不能合理地反映地下的地质构造。为了消除拾取的误差,本文采用局部回归法[6] 进行插值运算,这样就得到了平滑的速度场。
2.3.1 局部回归法三维插值原理首先定义一个平滑函数g (x),h = (x,y,z) ,并估计各个拾取点hi = (xi ,yi ,zi ) 的值di,然后建立模型公式如下:
| ${{d}_{i}}~(~{{h}_{i}}~)\text{ }=~g~(~{{h}_{i}}~)\text{ }+~{{\varepsilon }_{i}}$ | (2) |
式中:g ( hi ) 是di ( hi ) 的估计值,hi 为拾取点坐标,并假设εi 的平均值为0。
接着利用线性或二次多项式函数构建函数g( h),并通过最小二乘法建立函数如下 :
| $C\left( p,h \right)=\sum\limits_{i=1}^{N}{{{w}_{i}}}\left( h \right){{\left[ {{d}_{i}}\left( {{h}_{i}} \right)-f\left( p,{{h}_{i}} \right) \right]}^{2}}$ | (3) |
并设定改函数的权重函数当0 ≤ ui = ri / rN ≤ 1时,)
| ${{w}_{i}}={{\left[ 1-{{u}_{i}}{{\left( h \right)}^{3}} \right]}^{3}}$ | (4) |
否则:wi = 0
其中目标点距周围点距离
在εi 较大时,利用最小二乘法处理错误的拾取效果不好,因此引入一种迭代算法,构建一个加权函数为:
| ${{d}_{i}}~(~{{h}_{i~}})\text{ }=~g~(~{{h}_{i}}~)\text{ }+~{{\varepsilon }_{i}}~$ | (5) |
其中定义函数B 如下所示:
| $B\left( u \right)={{\left( 1-{{u}^{2}} \right)}^{2}},\left| u \right|\le 1$ | (6) |
在实际处理中用Wi 与wi 相乘,并重复上述步骤进行迭代运算,根据实际的效果确定迭代的次数,最终得到系数p 并计算出平滑的速度场。
2.3.2 实际数据处理验证下面利用局部回归法处理剩余速度分析所得到原始速度场,并通过效果对比选择以下参数:
N = 16,确定最大半径r =
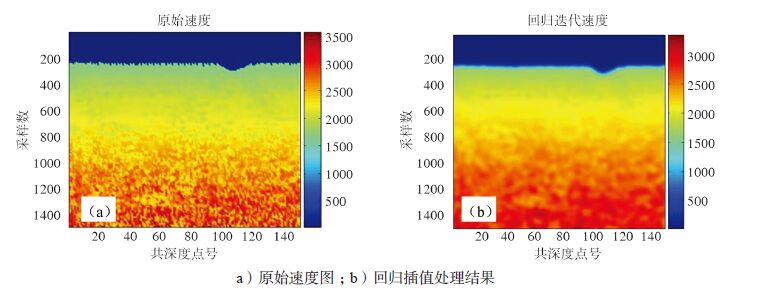 |
| 图 3 原始速度剖面与回归法处理后剖面对比 |
由图 3a 可见自动拾取的速度的连续性不好,尤其在深部这种现象更加明显。经过局部回归插值法的处理后有很大改善。由图 3b 中可见速度明显平滑许多,达到了预期的效果。
3 结论通过高精度剩余速度分析与常规叠加速度分析相比,可以得出以下结论:
(1)速度快:高精度剩余速度分析扫描速度范围小,针对性强,扫描速度比常规速度分析快。
(2)精度高:高精度剩余速度分析是在给定参考速度的基础上扫描剩余时差,扫描更加细致,精度更高。
(3)分辨率高:高精度剩余速度分析针对深层比浅层分辨率低的情况,采用随深度增加扫描速度间隔增大的动态扫描过程,这样扫描更具针对性,分辨率也更高。
高精度速度分析为动校正、偏移处理等提供准确的速度资料,更有利于以后的地震地质解释。
| [1] |
何樵登, 熊维纲.
应用地球物理教程——地震勘探. 北京:地质出版社[M]. 1991 .
( 0) 0)
|
| [2] |
徐翠娥, 郝晓红, 王影. 高精度双谱分析法在各向异性介质速度分析中的初步应用[J].
海洋石油,2008, 28 (1) : 1-5.
( 0) 0)
|
| [3] |
徐翠娥, 叶建兴, 周静毅. 基于叠前时间偏移速度扫描的四维建模技术及应用[J].
海洋石油,2008, 28 (2) : 25-28.
( 0) 0)
|
| [4] |
付强, 罗彩明. 基于VTI介质理论的P波速度分析和动校正[J].
物探化探计算技术,2008, 30 (1) : 10-16.
( 0) 0)
|
| [5] |
郭树祥. 高分辨率地震资料处理中的优化速度分析方法[J].
石油物探,2004, 43 (1) : 80-82.
( 0) 0)
|
| [6] |
ADLER F, BRANDWOOD S. Robust estimation of dense 3D stacking velocities from automated picking[C]. SEG Annual Meeting, 1999:1162-1165.
( 0) 0)
|
| [7] |
SILIQI R, LE MEUR D, GAMAR F,et al. High-density moveout parameter fields V and η[C]. Expanded Abstracts of 73rd Annual Internat SEG, 2003:2313-2316.
( 0) 0)
|
| [8] |
杜丽英, 刘国明, 杜丽娟, 等. VTI介质中地震波反射波合成记录的方法研究[J].
地球物理学进展,2001, 16 (2) : 58-64.
( 0) 0)
|
| [9] |
卢明辉, 唐建候. VTI介质P波非双曲时差分析[J].
地球物理学进展,2005, 20 (2) : 328-331.
( 0) 0)
|
| [10] |
孙祥, 娥詹毅, 钟本善. 双参数速度扫描方法研究[J].
石油天然气学报,2006, 28 (6) : 631-675.
( 0) 0)
|
 2016, Vol. 36
2016, Vol. 36

