| 地质图常用地图投影变形特征分析 |
地球的表面是一个极不规则的复杂曲面,为了便于科学研究,在测绘工作中,把地球当作一个扁率很小的参考椭球面来处理。椭球体上各点的相互位置,一般是由GPS测量、三角测量和天文测量得到并以经纬度表示。通过数学方法,将椭球体表面上的各点表示到平面图上,就形成了地图。为了符合视觉习惯,并易于在图上进行距离、方位、面积等量算和各种空间分析,地图通常都为平面。
地图由三类要素构成[1],第一类是数学要素,包括地图的坐标网、地图投影、比例尺等内容,它是编图的基础;第二类是地理要素,在地质图上主要体现为等值线、断层、井位标记等内容,它是地图的主体;第三类是辅助要素,是指为方便使用而提供的具有一定参考意义的说明性内容或工具性内容,主要包括图名、图号、图例、成图说明等内容。
地图投影作为地图的数学基础,地图投影的选择是否适当会直接影响成图的精度和实用价值。网络在线地图服务通常采用的是Web Mercator的地图投影方式,谷歌地图、百度地图均采用这种投影,图 1就是用Web Mercator投影做的一张世界地图,如果在该图中量取面积,会得到格林兰岛的面积比南美洲面积大的错误结论,实际上南美洲的面积约为1784×104km2,格陵兰岛的面积约为216.6×104km2,南美洲面积是格陵兰岛面积的8倍。因此根据地质制图任务的需要,选择一种最适宜的投影作为成图的数学基础,非常重要。
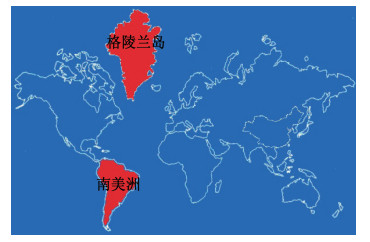 |
| 图 1 Web Mercator投影下的世界地图 |
1 地图投影 1.1 地图投影及其变形
无论把地球视为旋转椭球或是圆球,在数学上都是不可展开的曲面,而地图是一个平面,当椭球面或球面展开为平面时必然会产生破裂或褶皱。地图投影就是为了解决地图平面和地球曲面间的矛盾。
地图投影的实质就是按照一定的数学法则,将地球椭球面上的经纬网转换到平面上,建立地面点位的地理坐标(B,L)与地图上相对应的平面直角坐标(x,y)之间一一对应的函数关系。可以用下面的数学表达式表示:
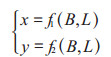
|
(1) |
地图投影中的变形,本质上是由于在曲面到平面的变换中,一点上不同方向长度变化不一致,以及不同点上同一方向的长度变化也不一致而产生的[2]。因此形成有长度、角度、面积方面的变形。图 2和图 3展示了不同投影下的地球上经纬网变形特征。
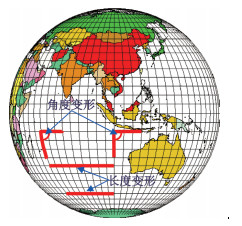 |
| 图 2 地图的长度、角度变形示意图 |
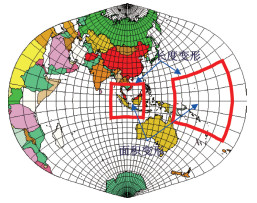 |
| 图 3 地图的长度、面积变形示意图 |
1.2 地图投影分类
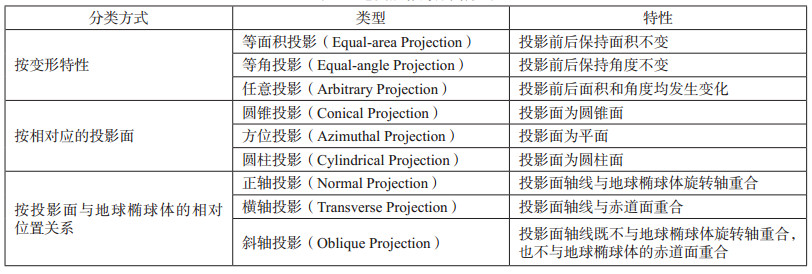
地图投影的种类多达数百种,一般按三种分类方式进行分类:①按投影的内在条件——投影的变形性质分类;②按投影的外在条件——正轴投影经纬网的形状分类;③按投影的外在条件——投影面与地球椭球间的相对位置关系分类。表 1列举了地图投影的分类方式及不同投影分类方式的特性。
| 表 1 地图投影的分类方式 |
2 地质图常用地图投影及其变形分析
地图投影种类很多,地质图件常用的投影有三种:高斯-克吕格投影、通用横轴墨卡托投影、墨卡托投影。
2.1 高斯-克吕格投影(Gauss-Kruger Projection)高斯-克吕格投影简称高斯投影,是一种等角横切椭圆柱投影。英美等一些国家称它为横轴墨卡托投影(TM投影),在Landmark等软件的投影设置中,没有高斯-克吕格投影选项,但有TM投影选项。图 4是高斯投影的示意图。
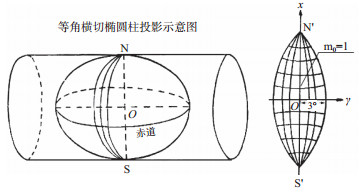 |
| 图 4 高斯投影示意图 |
高斯投影的中央经线和赤道为互相垂直的直线,其它经线均为凹向并对称于中央经线的曲线,其它纬线均为以赤道为对称轴并向两极弯曲的曲线,经纬线成直角相交。
高斯投影没有角度变形。中央经线长度比等于1,没有长度变形,其余经线长度比均大于1,长度变形为正,距中央经线愈远变形愈大,最大变形在边缘经线与赤道的交点上;面积变形也是距中央经线愈远,变形愈大。为了保证地图的精度,采用分带投影方法,即:将投影范围的东西界加以限制,使其变形不超过一定的限度。
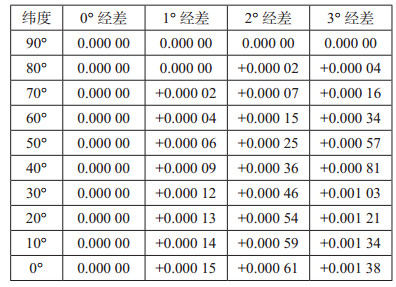
高斯投影最大长度变形为0.138%,最大面积变形为0.28%。表 2是高斯投影在6°带内长度变形表[3]。
| 表 2 高斯-克吕格投影6°带内长度变形表 |
2.2 通用横轴墨卡托投影(Universal Transverse Mercator)
通用横轴墨卡托投影即为常用的UTM投影,是一种等角横割圆柱6°分带投影。图 5为UTM投影的示意图。
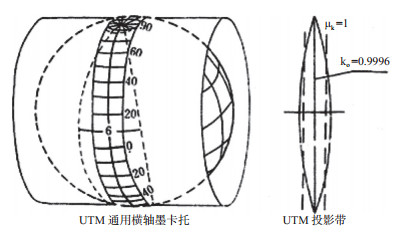 |
| 图 5 UTM投影示意图 |
UTM投影经纬框的形状和高斯投影相似,中央经线为直线,且为投影的对称轴,但中央经线上有长度变形,中央经线的长度比例因子取为0.999 6,是为了控制长度变形。
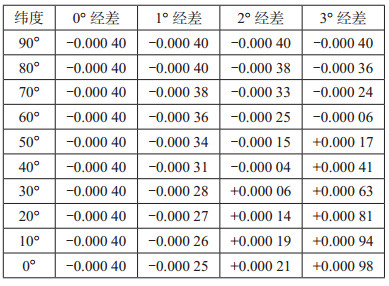
UTM投影的角度也没有变形。UTM投影的最大长度变形为0.098%,最大面积变形为0.2%。表 3是UTM投影的长度变形表[3]。
| 表 3 UTM投影长度变形表 |
2.3 墨卡托投影(Mercator Projection)
墨卡托投影又称正轴等角圆柱投影。假象一个与地轴方向一致的圆柱切或割于地球,按等角条件,将经纬网投影到圆柱面上,将圆柱面展为平面后,即得本投影。
如图 6所示,墨卡托投影的经纬线都是平行直线,且相交成直角,经线间隔相等,纬线间隔从标准纬线向两极逐渐增大。
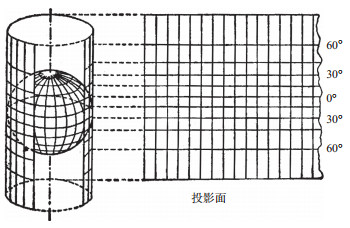 |
| 图 6 墨卡托投影示意图 |
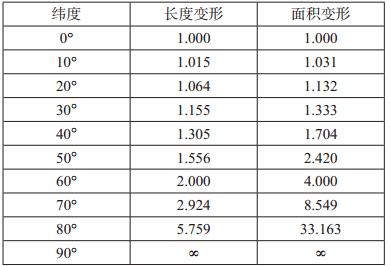
墨卡托投影没有角度变形,由每一点向各方向的长度比相等,墨卡托投影的地图上长度和面积变形明显,但标准纬线无变形,从标准纬线向两极变形逐渐增大,但因为它具有各个方向均等扩大的特性,保持了方向和相互位置关系的正确。在两极地区,长度、面积变形为无穷大。表 4是墨卡托投影长度和面积变形表[3]。
| 表 4 墨卡托投影长度和面积变形表 |
2.4 地质图不同地图投影的比较与应用
墨卡托投影在中、高纬度地区长度、面积变形很大,但其特点是等角航线表象成为直线,所以广泛用于编制航海图,也用于编制航空图[2]。
高斯投影和UTM投影的长度和面积变形相对较小,两者较为接近。我国规定1:50万~1:1万基本比例尺地形图采用高斯投影,所以在向国土管理部门提交地质图件时,通常要求是高斯投影平面坐标成果。美国、英国、加拿大等西方国家采用UTM投影作为常用的地形图投影方法,随着海域油气勘探的国际合作越来越多,我国海域油气勘探在实际使用中也常用UTM投影。
表 2、表 3显示,在距离中央经线1°范围内,纬度相同时高斯投影的长度变形比UTM投影的变形小,由于地球上微分圆的面积变形为长度变形的平方,因此该范围内高斯投影的面积变形也比UTM投影的面积变形小。在距离中央经线的2~3°时,随着纬度变小,高斯投影的长度、面积变形越来越大,而UTM投影的变形则相对较好。
以海外某勘探区块为例,该区块在经度143°00'~144°50'、纬度51°30'~52°30'范围内,利用其WGS84经纬度坐标采用不同投影计算了区块的面积,计算时高斯投影和UTM投影中央经线均设为141°。区块面积计算结果如下:高斯投影计算的面积为5 705.49 km2,UTM投影计算的面积为5 701.05 km2,墨卡托投影计算的面积为14 858.47 km2。利用等面积投影方式计算该区块的面积为5 700.24 km2,可当作是该区块的真实面积,高斯投影和UTM投影下的面积计算结果与其较为接近,UTM投影的变形更小;墨卡托投影的面积计算结果与真实面积差异太大。
东海油气勘探已有四十年历史。在二十世纪九十年代之前,东海油气勘探地质图件采用的投影方式为高斯投影,为了控制变形,中央经线没有选取标准6°分带21带的中央经线123°,而是选取中央经线为124°30'(靠近图幅中间)。近十几年,随着合作交流的增多,东海油气勘探地质图件越来越多采用UTM投影,中央经线为123°。以东海西湖凹陷斜坡带某三维工区为例,该区块在经度125°00'~125°30'、纬度29°50'~30°10'范围内,利用其WGS84经纬度坐标采用不同投影方式计算该区块的面积。区块面积计算结果如下:高斯投影中央经线为123°的计算结果为505.90 km2,高斯投影中央经线为124°30'的计算结果为505.37 km2,UTM投影中央经线123°计算结果为505.50 km2。利用等面积投影方式计算该区块的面积为505.30 km2,前面两种投影方式三种计算方法的结果与其相比,最大面积变形为0.12%,其中高斯投影中央经线为124°30'的面积变形最小,为0.01%。虽然东海西湖凹陷利用高斯投影和UTM投影带来的面积变形不大,但是在实际使用过程中仍需特别注意投影方式的选择,尤其是在利用以前老的地质图件或坐标成果时,投影使用不当时会造成严重错误。以西湖凹陷内一个经纬线交点为例,WGS84经纬度坐标为(125°,30°),采用不同投影计算该点的平面坐标:高斯投影中央经线为123°的计算结果是(692 992.30 m,3 321 798.01 m),高斯投影中央经线为124°30′的计算结果为(548 243.45 m,3 320 218.65 m),UTM投影中央经线为123°的计算结果是(692 915.11 m,3 320 469.29 m)。高斯投影中央经线为123°的计算结果与UTM投影中央经线123°计算结果相差1.3 km,高斯投影中央经线为124°30′的计算结果与UTM投影中央经线123°计算结果相差144.7 km。
3 结论地质图常用的高斯投影、UTM投影、墨卡托投影均为等角圆柱投影,这三种均有着不同程度的长度、面积变形。高斯投影、UTM投影的长度、面积变形较小,墨卡托投影的长度、面积变形普遍较大。在大范围区域进行面积精确计算时,建议选择等面积投影,例如亚尔勃斯等面积圆锥投影。在编制地质图件时投影方式的选择需要特别慎重。
| [1] |
宁津生, 陈俊勇, 李德仁, 等. 测绘学概论[M]. 湖北武汉: 武汉大学出版社, 2004: 78.
|
| [2] |
胡毓钜, 龚剑文. 地图投影图集[M]. 北京: 测绘出版社, 2006.
|
| [3] |
孙达, 蒲英霞. 地图投影[M]. 江苏南京: 南京大学出版社, 2005: 156-160.
|
 2015, Vol. 35
2015, Vol. 35