| 三维地震资料解释中时深转换方法对比分析及应用 |
地震资料解释是油田勘探开发研究工作的关键环节,时深转换是将地震资料解释成果转化为地质成果的必要过程。只有进行正确的时深转换,才能真实反映地下实际地质构造,获得可信和可靠的地质成果[1]。决定时深转换正确与否主要有三大要素:首先要有可靠的时间域t0图,这是正确进行时深转换的基础,同时精确的速度分析是时深转换的关键,在两者基础上选择合理的时深转换方法是时深转换的保证[2]。只有深刻把握这三大要素才能得到准确可靠的时深转换结果,从而提高构造成图的精度,减少深度误差。
目前,准确可靠的时深转换面临以下问题:一是对于构造简单、平均速度横向变化较小,钻孔分布均匀的地区,如何拟合公式正确选择时深关系式进行常速时深转换?二是对于构造复杂、平均速度横向变化剧烈,钻孔分布不均匀的地区,如何选取有效的变速成图方法提高成图的精度?对于常速成图,在经过合成地震记录标定获得时深后如何优选拟合式是研究的关键,对于变速成图,采用多种技术手段,根据不同的资料特征和实际情况选用不同的变速成图方法,进而对变速成图三种方法计算误差进行对比,说明各种方法的优越性和适用条件。
1 常速时深转换拟合式选择勘探早期因钻孔数量少,在构造形态变化较小、沉积平稳的地层往往根据工区内单井或多井层位标定获得的时深对拟合出在特定地区一定范围内适用的经验速度,如何优选拟合式成为常速时深转换的核心问题。通过对S探区多口井探讨各种时深关系式拟合效果的好坏,找出适用于不同条件的拟合关系式。
对S探区S1井的实测数据分别应用线性、二次和三次多项式以及幂函数拟合时深曲线(图 1)。
 |
| 图 1 S1井时深关系拟合曲线 |
三次多项式和幂函数拟合的时深关系式:
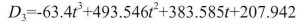
|
(1) |
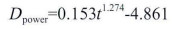
|
(2) |
式中:t-时间。
拟合相关系数平方分别为0.999 66和0.999 44。
经过比对,浅部地层三次多项式误差最小,拟合效果相对较好。深部地层幂函数误差最小,相对较优。三次多项式拟合时深公式应用于计算深部层速度时,会发生速度倒转(图 1、图 2), 这是因为速度是时深曲线的一阶导数。三次多项式的一阶导数是二次多项式,必然存在极值,因此不适用于深部;二次多项式拟合虽然不会导致速度倒转,但其速度向下匀速增大,也不符合速度向下减速增大的规律。乘幂在1和2之间的幂函数拟合式D=atb+c可同时近似浅部和深部的时深关系,是相对最优的关系式[3]。
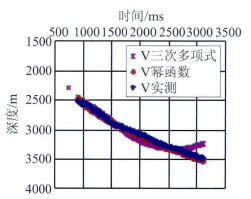 |
| 注:D1为线性拟合;D3为三次多项式拟合;Dpower为幂函数拟合。 图 2 S1井时速关系拟合曲线 |
时深关系拟合对一个工区来说不是单一公式,而是与目的层相匹配的几个公式,因为一般来说速度是随深度的加深逐渐增大,不同深度目的层时深关系是不同的,采用统一的速度解决地下不同的地质问题,不可避免地会产生认识上的偏差,因此对不同区块和不同目的层的构造研究及地质分析需分区分深度进行时深关系拟合。例如,某地区剖面从浅至深依次为新近系、古近系和前第三系。由于地震波的速度与地层的岩性有关,一般随地层变老,地震波传播速度增大,特别对前第三系碳酸盐岩和花岗岩来说速度相对于古近系地层速度更高,因此在进行时深转换时需分层对待,分别处理。
对该地区前第三系进行深度预测时,以周围临近井的时深为基础,选择合适的转换点(上覆地层岩性变化不大、地层产状比较平缓、上下地层速度变化较大)。在转换点之上,对临近井进行时深关系拟合得到一组关系式,而转换点之下对已钻井统计拟合出该地层单元的速度(ΔV), 重新建立适应该地层情况的时深表,从待转换地层统计不同地层单元的时间厚度(Δt), 运用关系式进行计算得出转换深度:
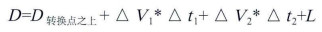
|
(3) |
式中:L-深度。
分段拟合时深关系在勘探早期钻井较少的稳定地层较为适用,但用统一的速度量版,忽略了地层速度的空间变化,平均效应明显,不够精确,随着勘探工作的进行和不断深入,愈发暴露出其缺陷。因此在构造形态及上覆地层厚度变化较大的地区采用变速成图。
2 变速成图方法对比应用 2.1 井空间插值法随着勘探不断深入,钻井数量增多,在构造平缓、纵横向速度变化较小的地区,根据工区内多井层位标定获得精度较高的速度资料进行纵横向插值求取速度场,这种插值方式在井间以距离作为权系数确定各井的速度数据在速度场中的贡献值,一般只考虑距离因素,不考虑地质结构的影响[4]。如何根据钻井的分布情况合理运用此方法成为井空间插值变速成图方法的关键。
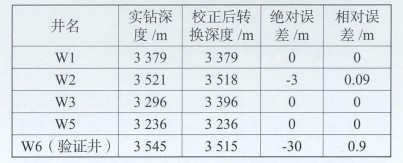
对W工区6口井运用井空间插值法求取速度场进行时深转换。从图 3、图 4中可以看出利用井空间插值法可得到速度场并且根据井空间插值得到的速度场将等t0图进行时深转换形成深度域构造图,从表 1中读出验证井的误差较大,通过分析认为造成验证井误差大的原因为:①井的数量有限;②井分布不均匀;③井间距太大(W6井距周边最近井的井距达到10 km以上)。
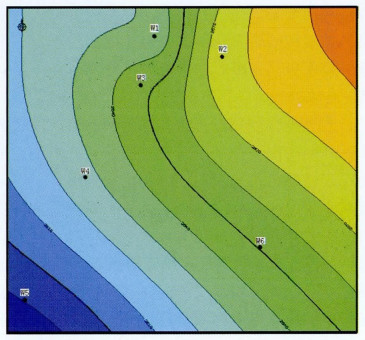 |
| 图 3 W工区东营组井间插值层速度等值线图 |
 |
| 图 4 W工区东营组构造图 |
| 表 1 W工区东营组时深转换误差对比 |
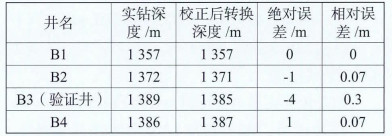
对某油田B构造4口探井运用井空间插值法进行构造成图,从表 2中可以看出各井的误差很小,这是因为B构造地层埋深比W工区东营组浅,构造平缓、起伏小,并且几口井分布均匀,井间距较小,大约为2 km左右,适合应用井空间插值法进行时深转换。
| 表 2 某油田B构造油层段时深转换误差对比 |
2.2 地质构造约束层速度变速成图
以少量井点资料为基础,以纯数学的距离内插方式生成速度场而不考虑实际地质结构变化对速度的影响,只能代表钻孔附近有限范围内的速度很精确,而离钻孔较远地方的速度,就不能用它来代替。如果探区内钻孔较少,且分布不均,地质情况比较复杂时,速度横向变化较大,钻孔之间的速度就很难求准。三维地震资料处理不仅提供叠加数据体,同时还提供三维叠加速度场,它的特点是全区分布均匀[5]。在复杂构造区,以层速度为基础,综合合成记录时深表、地震层位及钻井分层等多种数据类型,空间上采用层位和断层面等时地质构造为速度场外推的约束条件,井点以钻井分层作控制建立速度模型,从速度控制点到速度控制剖面,再进一步到速度体,建立起沿层位变化的、更为精确的层速度场(图 5),使时深转换后的地震数据体、断层、层位与实际钻井数据更加吻合,从而实现三维资料精确的时深转换,使构造保真性强(图 6)。
 |
| 图 5 某油田A构造基于地质模型约束层速度进行时深转换流程图 |
 |
| 图 6 某油田A构造东营组构造图(基于地质模型约束层速度的时深转换) |
基于地质模型约束层速度进行时深转换方法应用灵活,建场方式直观,精度较高,适合于各种复杂构造的时深转换,有良好的应用效果。
2.3 层叠法变速成图通过分析速度资料发现,许多井中地层层速度随深度增加变化趋势多样,这种变化用单一曲线描述存在较大误差。如果根据地层速度的垂向变化,多段采用线性变化趋势可以较好地描述速度的变化规律,具有较高的描述精度[6]。
首先根据工区及邻区速度随深度的变化趋势将地层划分为大层,利用VSP、声波测井等速度资料,根据速度变化趋势划分速度段,建立各层层速度v0平面图;分段拟合速度,求取各段的vp和k;然后计算层速度;利用各层的层速度和时间计算各层的厚度,最后通过多层累加,实现成图[7]。
该方法是以vp-k。岳线性速度模型为基础[8]。
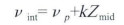
|
(4) |
式中:vint-层速度,
vp-截距,
k-斜率,
Zmid-目的层段中点深度。
该式物理意义为,在相同的构造背景下形成的同类岩性地层的层速度随着深度增加线性增加。
叠加速度体经Dix公式转成层速度、平均速度体,沿层提取速度得到各大层速度框架,然后运用测井资料计算出各小层段的层速度和各层中点深度拟合出一条直线,其斜率为k,截距vp。值,再求取未知点的层速度。
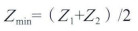
|
(5) |
式中:Z1-第1层深度,已知;
Z2-第2层深度。
Z2还可以表示为:
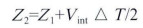
|
(6) |
式中:ΔT-第2层的双程时间,
将式(5)、式(6)代入式(4),得出层速度表达式
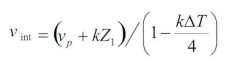
|
(7) |
利用(7)式可计算第2层的层速度,进而求出第2层的深度。依此类推,可计算出各层的层速度v、层间厚度Δh和顶面深度H(图 7)。
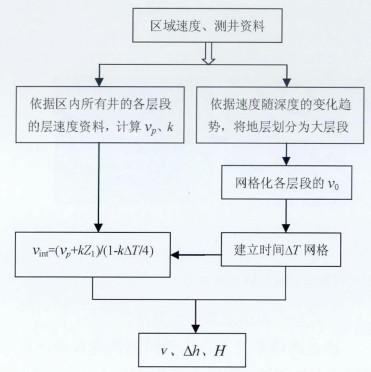 |
| 图 7 层叠法实现流程图 |
在L工区运用层叠法变速成图进行时深转换,根据岩性变化特征和解释层位,将地层从上至下依次划分为东营组一段、东营组二段、沙河街组二段、沙河街组三段,在此基础上,运用区域速度资料分别提取各层的层速度v0,利用区内及邻区5口井资料分层拟合,得到各小层的vp、k,利用前述公式算出各小层的层速度、层间厚度和顶面深度。图 8为东营组二段的拟合情况,相关系数平方为0.964 3,相关性较好。
 |
| 图 8 L工区东营组二段vp和k拟合曲线 |
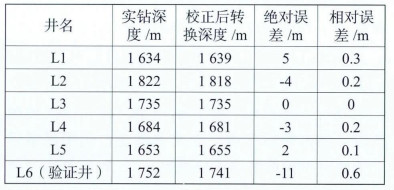
L工区东营组二段运用层叠法变速成图,通过5口井的层顶深度与钻井深度比对,相对误差均小于0.3%,而验证井层顶深度与钻井深度相差11 m,小于1%(表 3),吻合度较高,说明层叠法变速成图方法较好地反映了地下构造特征(图 9)。
| 表 3 东营组二段时深转换深度误差对比 |
 |
| 图 9 L工区东营组二段构造图 |
3 结论
通过分析和讨论,指出几种时深转换技术的应用及注意事项,总结出各种方法的优劣和应用范围,同时对目前时深转换问题有如下几点认识:
(1) 对于常速成图,分区和分深度进行幂函数拟合是最理想的办法,针对不同地区、不同目的层的构造研究及地质分析,可分区对多口井进行幂函数拟合,从中选择相对最优的拟合式。
(2) 在实际应用中可根据不同的资料特征和实际情况选用不同的变速成图方法,为消除各种误差,需采用多种技术手段处理计算均方根速度和平均速度,使得到的速度场满足生产要求。
(3) 在时深转换过程中要注重细节、精益求精,努力提高构造图的精度,降低勘探风险,提高油气勘探的成功率。
| [1] |
陈广军. 古生界时深转换关系探讨[J]. 断块油气田, 2001, 8(6): 19-22. |
| [2] |
何际平, 鲁烈琴, 王红旗, 等. 复杂地区速度场建立与变速构造成图方法研究[J]. 地球物理学进展, 2006, 21(1): 167-172. |
| [3] |
周蒂, 胡登科, 何敏, 等. 深部地层时深转换中的拟合式选择问题[J]. 中国地质大学学报(地球科学), 2008, 33(4): 531-537. |
| [4] |
张华军, 王海兰, 肖富森, 等. 基于反射层的变层速度模型时深转换方法[J]. 天然气工业, 2003, 23(1): 36-38. |
| [5] |
龚幸林, 林建东. 煤田三维地震资料解释的时深转换方法研究[J]. 中国煤田地质, 2002, 14(2): 65-67. |
| [6] |
Marsden D, Bush M D, Johllg D s. Analytic velocity functions[J]. The Leading Edge, 1995, 14(7): 775-782. DOI:10.1190/1.1437161 |
| [7] |
袁井菊. 层叠法变速构造成图的地质基础及其应用[J]. 石油物探, 2006, 45(3): 285-289. |
| [8] |
Keho T, Samsu D. Depth conversion of Tangguh gas field[J]. The Leading Edge, 2002, 21(10): 966-971. DOI:10.1190/1.1518432 |
 2014, Vol. 34
2014, Vol. 34