2. 河南省安阳市疾病预防控制中心;
3. 河南省中医药大学
五氯酚(pentachlorophenol,PCP)及其钠盐五氯酚钠(sodium pentachlorophenate,NaPCP)属有机氯农药,主要被用作除草剂、杀虫剂和防腐剂。可经皮肤、消化道、呼吸道吸收进入哺乳动物体内,并蓄积于肝、肾、胆囊和脂肪等器官和组织,有导致新生儿先天畸形和哺乳动物生殖细胞畸形等生殖发育毒性风险,并在染色体和基因水平上具有潜在的遗传毒性风险,对人体健康构成极大威胁[1-2]。在动物源性食品五氯酚残留量的测定中不确定度是与测量结果相关联的参数,为确保结果的可信度, 必须进行不确定度的评估。本方法参照《2018年国家食品污染物和有害因素风险监测工作手册》中《动物组织及鸡蛋中五氯酚钠测定的标准操作程序》及相关文献[3-4],采用基质匹配标准曲线来降低基质对定量的干扰, 通过添加内标物质, 采用SLC柱净化,乙酸酐—吡啶衍生的方法对样品进行前处理, 气相色谱—三重四极杆质谱仪进行测定, 并根据《测量不确定度评定与表示》(JJF 1059.1-2012)[5]、《化学分析测量不确定度评定》(JJF 1135-2005)[6]中规定的程序和方法及相关文献[7-13], 对动物组织中五氯酚的测定进行不确定度来源的分析和评估, 确定影响测定结果的主要来源, 为进一步探讨测量结果的准确程度和方法的可靠性提供参考。
1 材料与方法 1.1 仪器与试剂7890 A/7000 GC-MS/MS(Agilent公司,美国);涡旋混匀器(Scientific Industries公司,美国);ME1002/02电子天平(瑞士梅特勒—托利多公司);冷冻离心机Eppendorf 5920 R德国;匀浆机(德国IKA T25);移液器(eppendorf德国)。五氯酚标准储备液(100μg/mL,甲醇):农业部环境保护科研监测所,编号GSB05-1850-2008;2,4,6-三溴酚(1.03 mg/mL,甲醇)GBW(E)080473中国计量科学研究院;正己烷、丙酮、乙腈、乙酸乙酯(德国Merk公司)均为色谱纯;无水硫酸钠、碳酸钾、乙酸酐、吡啶分析纯。SLC固相萃取柱或等效固相萃取柱:500 mg/6mL(氧化铝+SCX)。
1.2 方法 1.2.1 色谱条件DB-5MS毛细管色谱柱(30 m×0.25 mm×0.25 μm,美国Agilent公司);进样口温度:230℃;载气:高纯氦气(纯度≥99.999%);流速1.0 mL/min;程序升温:80℃保持2 min,再以10℃/min的速度升至250℃,最后以40℃/min的速度升至290℃,保持4 min;进样方式:不分流进样;进样体积:1.0 μL。
1.2.2 质谱条件电离方式为电子轰击源(EI);电离能量70 ev;溶剂延迟3 min;离子源温度:230℃;传输线温度:250℃;监测方式选择离子扫描(SIM);五氯酚衍生物五氯苯乙酸酯定性离子m/z为264、268和308,定量离子266;内标物2,4,6-三溴酚衍生物2,4,6-三溴苯乙酸酯定性离子m/z为328、332,定量离子330。
1.2.3 样品前处理各称取5.00 g猪肉、鸡肉、淡水鱼等动物组织绞碎样品入50 mL离心管内,加入30 μL 10.0 μg/mL 2, 4, 6-三溴酚内标液、20 mL 5%三氯乙酸溶液,匀浆1 min, 再加入10 mL乙酸乙酯:正己烷=1 :9(V :V)提取液,涡旋提取2 min,然后0℃ 12 000 rpm离心4 min,吸出上层有机相入15 mL离心管内,在60℃水浴内氮气吹干,加入2.0 mL乙腈超声溶解、提取,离心半径140 mm、8 000 rpm离心2 min,上层乙腈相过SLC柱净化,乙腈洗脱收集,洗脱液60℃氮气吹至0.5 mL左右, 残余物加衍生试剂0.2 mL衍生,密封,于60℃水浴反应15 min,取出冷却,加1 mL正己烷、0.2 mol/L碳酸钾溶液2.0 mL,充分混匀提取,8 000 rpm离心2 min,取有机相,供气相色谱质谱测定。
1.2.4 标准曲线的制备取10、25、50、100和200 μL 1.0 mg/L五氯酚标准使用液,分别加入30 μL 10.0μg/mL 2, 4, 6-三溴酚内标液、0.5 mL乙腈、0.2 mL衍生试剂,密封,同1.2.3样品前处理一起衍生、提取,获得10、25、50、100、200 ng五氯酚标准曲线。根据内标法标准曲线计算样品中五氯酚的含量C。
1.2.5 样品检测与计算以五氯酚衍生物五氯苯乙酸酯的峰面积与内标2,4,6-三溴酚衍生物2,4,6-三溴苯乙酸酯的峰面积之比(Y)对五氯酚的质量(X, ng)进行线性回归,得到标准工作曲线,由标准工作曲线计算五氯酚的质量,按下式计算样品中五氯酚含量按式(1)计算,结果保留三位有效数字:
| $ C = \frac{A}{m} $ | (1) |
式中:C —实际样品中五氯酚含量,μg/kg;
A—由标准曲线计算试样中五氯酚的质量,ng;
m—取样量,g。
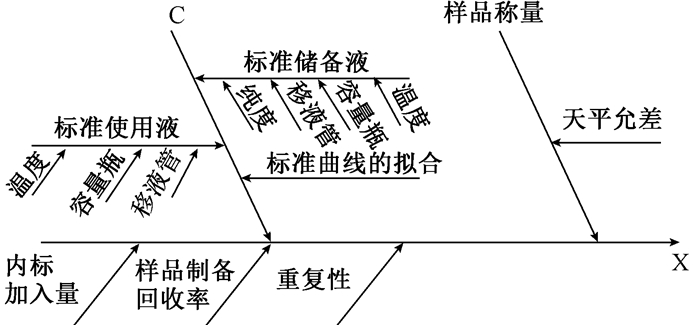
2 不确定度的来源分析整个实验流程,不确定度的来源主要有:样品称量、重复性(随机效应)、回收率(样品处理)、内标加入量、标准溶液的配制以及标准曲线的拟合等因素。不确定度因果图见图 1。
|
| 图 1 不确定度因果图 |
3 不确定度评定 3.1 样品称量(W)引入的不确定度
称取5.00 g样品,据天平检定证书其最大允许误差为±0.01 g, ,按均匀分布处理(
| $ u{\left( W \right)_0} = \frac{a}{k} = \frac{{0.01}}{{\sqrt 3 }} = 0.005\;8\;{\rm{g}} $ | (2) |
该标准不确定度需计算两次,一次为皮重,一次为总重,则称量带入的标准不确定度为:
| $ u\left( W \right) = \sqrt {2 \times u\left( W \right)_0^2} ,u\left( W \right) = 0.008\;2\;{\rm{g}} $ | (3) |
称量引入的相对不确定度:
| $ {u_{rel}}\left( W \right) = \frac{{u\left( W \right)}}{W} \times 100\% = 0.16\% $ | (4) |
在相同条件下,对某一猪肉样品进行6次重复测定, 测定结果分别为5.21、5.15、5.18、5.24、5.12、5.35 μg/kg平均浓度5.21 μg/kg,根据贝塞尔公式进行不确定度计算:标准差:
| $ s\left( x \right) = \sqrt {\frac{1}{{n - 1}}\sum\limits_{i = 1}^n {{{\left( {{x_i} - \bar x} \right)}^2}} } = 0.085\;{\rm{ \mathsf{ μ} g/kg}} $ | (5) |
重复性标准不确定度:
| $ u\left( {rep} \right) = \frac{{s\left( x \right)}}{{\sqrt n }} = \frac{{0.085}}{{\sqrt 6 }} = 0.035\;{\rm{ \mathsf{ μ} g/kg}} $ | (6) |
重复性的相对不确定度:
| $ \begin{array}{l} {u_{rel}}\left( {rep} \right) = \frac{{u\left( {rep} \right)}}{{\bar x}} \times 100\% = \frac{{0.035}}{{5.21}} \times 100\% \\ \;\;\;\;\;\;\;\;\;\;\;\;\; = 0.67\% \end{array} $ | (7) |
样品前处理过程繁琐,需经过均质、提取、净化、浓缩、衍生等多步,每步都会引入不确定度,但却难于定量每步对不确定度的贡献,一般采用方法加标回收率、精密度等数据来计算此过程引入的不确定度问题,本文采用加标回收率进行评定。在样品猪肉(五氯酚含量5.21 μg/kg)中添加五氯酚标液100 ng,进行6次重复检测, 测定结果如表 1。
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 取样量/g | 5.00 | 5.00 | 5.00 | 5.00 | 5.00 | 5.00 |
| 本底值/(μg/kg) | 5.21 | 5.21 | 5.21 | 5.21 | 5.21 | 5.21 |
| 加标量/ng | 100 | 100 | 100 | 100 | 100 | 100 |
| A五氯酚/A内标 | 0.211 5 | 0.221 3 | 0.222 7 | 0.210 5 | 0.204 7 | 0.208 8 |
| 检出质量(μg/kg) | 122.1 | 127.6 | 128.3 | 121.6 | 118.3 | 120.6 |
| 回收率/% | 96.0 | 101.5 | 102.2 | 95.5 | 92.2 | 94.5 |
根据贝塞尔公式,标准差及平均值:
| $ \begin{array}{l} s(R) = \sqrt {\frac{1}{{n - 1}}\sum\limits_{i = 1}^n {{{\left( {{x_i} - \bar x} \right)}^2}} } = 3.99\% \\ \bar R = 97.0\% \end{array} $ | (8) |
回收率标准不确定度:
| $ u(R)=\frac{s(R)}{\sqrt{n}}=1.63 \% $ | (9) |
回收率相对不确定度:
| $ u_{r e l}(R)=\frac{u(R)}{\overline{R}} \times 100 \%=1.68 \% $ | (10) |
用检测统计数据t对平均回收率进行显著性检验,在95%置信概率,自由度n=5时的t分布临界值t0.95(5)=2.57,即当检验值t≥2.57时, 则与回收率100%有显著性差异, 须使用回收率修正结果;反之则无需采用回收率修正结果。
| $ t=\frac{|1-\overline{R}|}{u_{\mathrm{rel}}(R)}=\frac{|1-0.970|}{0.0168}=1.79 $ | (11) |
t < t0.95(5),回收率和1之间无显著性差异,可以不做回收率校正。
3.4 加入内标使用液带入的不确定度(V)根据内标法原理, 由于样品溶液与标准系列溶液始终加入同一份内标物, 在定量计算过程中内标物浓度可约除, 因此在配制内标溶液时无需精密操作, 不考虑内标物纯度引起的不确定度, 只考虑标准曲线绘制和样品稀释过程中量取内标物体积时引入的不确定度。
用量程40 μL移液器吸取30 μL内标使用液(10.0 μg/mL),根据《移液器检定规程》 (JJG 646-2006)[11]规定40 μL可调移液器吸取30 μL时容量最大允许误差为±4.0%,按矩形分布,(
标准不确定度为:
| $ u(V)=\frac{a}{k}=\frac{40 \times 4.0 \%}{\sqrt{3}}=0.92 \ \rm{ \mathsf{ μ} } \mathrm{L} $ | (12) |
内标引入相对标准不确定对为:
| $ u_{r e l}(V)=\frac{u(V)}{30} \times 100 \%=3.07 \% $ | (13) |
样品溶液中五氯酚测定浓度(C)带入不确定度由五氯酚标准溶液浓度、标准溶液的配制以及标准曲线拟合三部分带入。
3.5.1 标准品引入的不确定度五氯酚原标准溶液浓度引起的相对不确定度评定。五氯酚标准储备液(100 μg/mL,扩展不确定度0.13 μg/mL甲醇):农业部环境保护科研监测所,编号GSB05-1850-2008,则五氯酚标液引入的相对标准不确定对为:
| $ u_{r e l}(c)_{1}=\frac{u\left(c_{0}\right)}{\mathrm{k} \times c_{0}} \times 100 \%=0.065 \% $ | (14) |
式中:u(c0)—标准溶液证书上的不确定度;
c0—标准溶液浓度;
扩展因子k=2。
3.5.2 标准使用液配制带入的不确定度五氯酚标准使用液为用量程为250 μL移液器吸取250 μL标准储备液于25.0 mL容量瓶中,丙酮定容配制而成,浓度为1.0 μg/mL。标准中间液配制带入不确定度包括三部分,250 μL移液器(v0)、容量瓶(v)、及温度变化(T)。
250 μL移液器(v0)根据《移液器检定规程》 (JJG 646-2006)[11]规定250 μL可调移液器吸取250 μL时容量最大允许误差为±1.5%,按矩形分布,(
标准不确定度为:
| $ u(V)=\frac{a}{k}=\frac{1.5}{\sqrt{3}}=0.87 \ \rm{ \mathsf{ μ} } \mathrm{L} $ | (15) |
相对标准不确定对为:
| $ u_{r e l}\left(v_{0}\right)=\frac{u(V)}{250} \times 100 \%=0.35 \% $ | (16) |
25 mL容量瓶(根据JJG 196-2006,A级允差±0.03 mL),按矩形分布(
| $ u(v)=\frac{0.03}{25 \times \sqrt{3}} \times 100 \%=0.069 \% $ | (17) |
温度变化(T):由于温度波动引起的体积变化,实验室温度波动范围为(20±5)℃,按均匀分布,
产生的体积变化V=±(25×1.49×10-3×5)=±0.19 mL,
| $ u(T)=\frac{0.19}{25 \times \sqrt{3}} \times 100 \%=0.44 \% $ | (18) |
配制标准使用液带入的相对不确定度为:
| $ u_{r e l}(c)_{2}=\sqrt{u(v)^{2}+u(T)^{2}+u\left(v_{0}\right)^{2}}=0.57 \% $ | (19) |
对5个不同浓度的五氯酚标准溶液进行测定(表 2)。以系列标准溶液中五氯酚含量为横坐标, 五氯酚与内标物丰度比值(A五氯酚/A内标)为纵坐标, 由最小二乘法原理进行拟合求得标准曲线,y=0.001 8x-0.007 6,R2=0.998 7。
| 质量/ng | 10.0 | 25.0 | 50.0 | 100.0 | 200.0 |
| 响应值 | 0.014 9 | 0.035 4 | 0.076 7 | 0.171 4 | 0.348 9 |
| 0.013 7 | 0.033 4 | 0.074 5 | 0.176 7 | 0.341 2 | |
| 0.015 2 | 0.032 1 | 0.077 2 | 0.182 1 | 0.352 9 | |
| 平均值(Ai) | 0.014 6 | 0.033 6 | 0.076 1 | 0.176 7 | 0.347 7 |
| a+bc | 0.010 4 | 0.037 4 | 0.082 4 | 0.172 4 | 0.352 4 |
| 计算值ci | 12.3 | 22.9 | 46.5 | 102.4 | 197.4 |
对样品猪肉(五氯酚含量5.21 μg/kg)测定6次,响应值分别为:0.039 29、0.038 75、0.039 02、0.039 56、0.038 48、0.040 55带入方程求得浓度(ng)为26.1、25.8、25.9、26.2、25.6、26.8,cc=26.0 ng。
标准曲线标准差:
| $ {s_A} = \sqrt {\frac{{\sum\limits_{i = 1}^n {{{\left[ {{A_i} - \left( {a + b{c_i}} \right)} \right]}^2}} }}{{n - 2}}} $ | (20) |
| $ \begin{array}{*{20}{c}} {SA = 0.0061,\bar c = (10 + 25 + 50 + 100 + 200)/5 = 77}\\ {u{{(c)}_3} = \frac{{{s_A}}}{b}\sqrt {\frac{1}{p} + \frac{1}{n} + \frac{{{{\left( {{c_c} - \bar c} \right)}^2}}}{{\sum\limits_{i = 1}^n {{{\left( {{c_i} - \bar c} \right)}^2}} }}} } \end{array} $ | (21) |
式中:sA—标准曲线的标准差;
p—样品溶液的测定次数(p=6);
n—标准溶液的测定总次数(n=15);
b—标准曲线的斜率;
a—标准曲线的截距;
cc—由标准曲线求得的样品溶液中浓度;
c—各标准溶液中浓度的平均值;
ci—由标准曲线方程得出的标准溶液中浓度的测定值。
| $ \begin{array}{*{20}{l}} {u{{(c)}_3} = \frac{{0.006\;1}}{{0.001\;8}} \times \sqrt {\frac{1}{6} + \frac{1}{{15}} + \frac{{{{(26.0 - 77)}^2}}}{{{{(12.3 - 77)}^2} + {{\left( {22.9 - 77} \right)}^2} + {{(46.5 - 77)}^2} + {{(102.4 - 77)}^2} + {{(197.4 - 77)}^2}}}} }\\ {u{{(c)}_3} = 1.99} \end{array} $ |
标准曲线拟合带来的相对不确定度:
| $ u_{r e l}(C)_{3}=\frac{U(C)_{3}}{C_{c}} \times 100 \%=7.62 \% $ | (22) |
样品溶液(c)带入总的相对标准不确定度为
| $ \begin{array}{*{20}{c}} {{u_{rel}}(c) = \sqrt {{u_{rel}}(c)_1^2 + {u_{rel}}(c)_2^2 + {u_{rel}}(c)_3^2} }\\ {{u_{rel}}(c) = 7.64\% } \end{array} $ | (23) |
合成不确定度,计算公式如下
| $ {u_{r e l}(X)=\sqrt{u(w)^{2}+u(r e p)^{2}+u(V)^{2}+u(c)^{2}}} \\ {u_{r e l}(X)=\sqrt{0.16^{2}+0.67^{2}+3.07^{2}+7.64^{2}}=8.26 \%} $ | (24) |
依据标准《测量不确定度评定与表示》(JJF1059.1-2012)[5],对大多数测量不确定评估,取置信水平95 %,k=2,则本试验中五氯酚含量的相对扩展不确定度为:
| $ \begin{array}{*{20}{c}} {U = {u_{rel}}(X) \times k \times {\rm{\bar X}}}\\ {U = 8.26\% \times 2 \times 5.21\;{\rm{ \mathsf{ μ} g}}/{\rm{kg}} = 0.86\;{\rm{ \mathsf{ μ} g}}/{\rm{kg}}} \end{array} $ | (25) |
| $ X = (5.21 \pm 0.86){\rm{ \mathsf{ μ} g}}/{\rm{kg}}(k = 2,p = 95\% ) $ |
| 项目 | 分量 | 相对标准不确定度/% |
| 重复性 | rep | 0.67 |
| 回收率 | R/% | 1.68 |
| 样品称量 | m/mg | 0.16 |
| 内标加入量 | V/μL | 3.07 |
| 标准溶液配制 | C1+ C2 | 0.57 |
| 标准曲线拟合 | C3 | 7.64 |
|
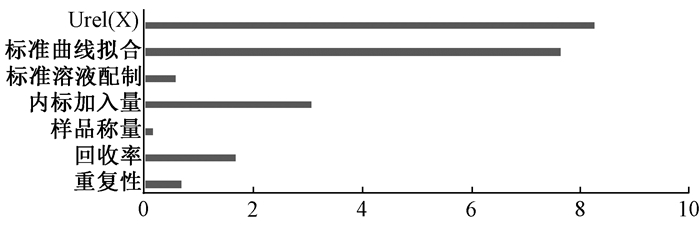
| 图 2 各相对标准不确定度分量柱状图 |
5 讨论
本次评定将样品处理过程中的提取、净化、衍生等操作带来的不确定度,通过计算回收率的不确定度来表示。通过分析气相色谱—三重四极杆质谱法测定动物组织中五氯酚的不确定度来源,分别评价后进行合成扩展。五氯酚浓度的不确定度主要由重复性、回收率、内标加入量和标准曲线拟合引入。标准曲线拟合和内标加入量的影响最大,其次是重复性与回收率,称取样品所带来的不确定度可以忽略不计。因此,在实际操作过程中,可以通过增加标准系列溶液的测定次数,控制内标加入量,增加平行样品测定以减小测量不确定度,从而保证检测结果的准确性。
| [1] |
夏勇, 董晓岚, 孟真, 等. 五氯酚钠的发育毒性和遗传毒性研究[J]. 预防医学, 2016, 28(11): 1081-1086. (In English: Xia Y, Dong XL, Meng Z, et al. A study on the development toxicity and genetoxicity induced by sodium pentachlorophenate[J]. Prev Med, 2016, 28(11): 1081-1086.) |
| [2] |
许文青, 樊柏林, 陈明, 等. 五氯苯酚和五氯苯酚钠毒性作用研究进展[J]. 中国药理学与毒理学杂志, 2011, 25(6): 596-600. (In English: Xu WQ, Fan BL, Chen M, et al. Progress in toxicity of pentachlorophenol and sodium pentachlorophenol[J]. Chin J Pharmacol Toxicol, 2011, 25(6): 596-600. DOI:10.3867/j.issn.1000-3002.2011.06.014) |
| [3] |
国家卫生和计划生育委员会. GB 23200.92-2016动物源性食品中五氯酚残留量的测定液相色谱-质谱法[S].北京: 中国标准出版社, 2017. (In English: In English: National Health and Family Planning Commission of PRC. GB 23200.92-2016 National food safety standards-Determination of pentachlorophenol residue in animal-derived foods[S]. Beijing: Standards Press of China, 2017.)
|
| [4] |
农业部. GB 29708-2013动物性食品中五氯酚钠残留量的测定气相色谱-质谱法.[S].北京: 中国标准出版社, 2014. (In English: In English: Ministry of Agriculture GB 29708-2013 Determination of sodium pentachlorophenol residue in animal derived food by Gas Chromatography-mass spectrometry method Beijing: Stand Press of China, 2014).)
|
| [5] |
中华人民共和国国家质量监督检验检疫总局. JJF 1059.1-2012测量不确定度评定与表示[S].北京: 中国标准出版社, 2013. (In English: In English: General Administration of Quality Supervision, Inspection and Quarantine of the People's Republic of China. JJF 1059.1-2012 Evaluation and expression of uncertainty in measurement[S]. Beijing: Standards Press of China, 2013.)
|
| [6] |
中华人民共和国国家质量监督检验检疫总局. JJF 1135-2005化学分析测量不确定度评定[S].北京: 中国计量出版社, 2005. (In English: In English: General Administration of Quality Supervision, Inspection and Quarantine of the People's Republic of China. JJF 1135-2005 Evaluation of uncertainty in chemical analysis measurement[S]. Beijing: China Metrology Publishing House, 2005.)
|
| [7] |
中华人民共和国国家质量监督检验检疫总局. GB/T 27418-2017测量不确定度评定和表示[S].北京: 中国标准出版社, 2018. (In English: In English: General Administration of Quality Supervision, Inspection and Quarantine of the People's Republic of China. GB/T 27418-2017 Guide to the evaluation and expression of uncertainty in measurement[S]. Beijing: Standards Press of China, 2018.)
|
| [8] |
中国合格评定国家认可委员会. CNAS-GL06-2006化学分析中不确定度的评估指南[S].北京: 中国计量出版社, 2006. (In English: In English: China National Accreditation Service for Conformity Assessment. CNAS-GL06-2006 Guidance on evaluating the uncertainty in chemical analysis[S]. Beijing: China Metrology Publishing House, 2006.)
|
| [9] |
韩嘉艺, 李晓明, 钱乐, 等. 微量分光光度法测定饮用水中亚硝酸盐氮检测结果的有效性评估[J]. 环境卫生学杂志, 2016, 6(5): 360-364. (In English: Han JY, Li XM, Qian Y, et al. Assessment on validity nitrite-nitrogen results in drinking-water by micro-spectro photometry[J]. J Environ Hyg, 2016, 6(5): 360-364.) |
| [10] |
中国合格评定国家认可委员会. CNAS-CL01检测和校准实验室能力认可准则[S].北京: 中国计量出版社, 2018. (In English: In English: China National Accreditation Service for Conformity Assessment. CNAS-CL01 Accreditation criteria for the competency of testing and calibration laboratories[S]. Beijing: China Metrology Publishing House, 2018)
|
| [11] |
中华人民共和国国家质量监督检验检疫总局. JJG 646-2006移液器检定规程[S].北京: 中国计量出版社, 2007. (In English: In English: General Administration of Quality Supervision, Inspection and Quarantine of the People's Republic of China. JJG 646-2006 Verification regulation of locomotive pipette[S]. Beijing: China Metrology Publishing House, 2007.)
|
| [12] |
中华人民共和国国家质量监督检验检疫总局. JJG 196-2006常用玻璃量器检定规程[S].北京: 中国计量出版社, 2007. (In English: In English: General Administration of Quality Supervision, Inspection and Quarantine of the People's Republic of China. JJG 196-2006 Verification regulation of working glass container[S]. Beijing: China Metrology Publishing House, 2007)
|
| [13] |
刘芳芳, 魏秋宁, 丁亚磊. 氢化物原子荧光法测定尿中砷的不确定度分析[J]. 环境卫生学杂志, 2018, 8(4): 350-354. (In English: Liu FF, Wei QN, Ding YL. Uncertainty evaluation on the determination of arsenic in urine by hydride generation atomic fluorescence spectrometry[J]. J Environ Hyg, 2018, 8(4): 350-354.) |

