2. 兰州大学基础医学院;
3. 兰州大学第二医院内分泌科;
4. 白银市第二人民医院;
5. 兰州大学公共卫生学院
近年来,与饮用水有关的突发公共卫生事件逐渐增多,当饮用水受到病原体的污染后,可引起多种水相关疾病的流行,其对居民健康的影响不容忽视。我国公共卫生专家将霍乱、伤寒、副伤寒以外的感染性腹泻等疾病列入“水相关疾病”范畴[1],研究结果显示,水相关疾病的发病呈现一定的季节性和周期性[2-4]。随着计算机的逐步推广应用以及疾病预测理论的迅速发展,已有多种预测方法在传染病的预防与控制中得到了实际应用。目前,用于预测的模型主要包括指数平滑法、线性回归法、自回归分析、隐马尔可夫模型、时间序列分析等模型。时间序列预测是一种考虑对象本身的历史数据随时间发展变化的规律,并用该变量以往的资料建立统计模型做外推的预测方法。自回归求和移动平均(auto regressive integrated moving average,ARIMA)乘积季节模求是时间序列分析中重要而基本的模型之一,已广泛应用于传染病发病率的预测,特别是具有季节性趋势的传染病预测。本文运用R软件基于ARIMA模型对兰州市2006—2017年水相关疾病发病情况进行分析与预测,并初步探索时间序列分析在水相关疾病预测中的应用。
1 资料与方法 1.1 资料来源借助全国传染病报告信息管理系统平台,收集2006—2017年兰州市伤寒、霍乱、细菌性痢疾等水相关疾病发病数据。
1.2 研究内容采用时间序列乘积季节模型构建2006—2014年兰州市水相关疾病月发病率数据模型,利用2015—2017年数据对模型效果进行检验。
1.3 ARIMA乘积季节模型的构建ARIMA模型是一种基于时间序列分析和预测的方法。随机季节模型与ARIMA模型结合即为ARIMA季节模型,一般表示为ARIMA (p,d,q)×(P,D,Q) s。各参数的意义:非季节自回归阶数p、非季节差分阶数d、非季节移动平均阶数q,季节自回归阶数P、季节差分阶数D和季节移动平均阶数Q,季节长度S。当P=D=Q=0时,该模型为ARIMA模型。ARIMA乘积季节模型能综合考虑季节、趋势和随机干扰等因素,对时间序列预测效果较好。建模过程:①序列平稳:通过“tseries”软件包中的“ts”函数将2006年l月—2017年12月水相关疾病发病率定义为以月为单位的时间序列,利用“plot.ts”函数绘制并分解时间序列,观察时间序列的趋势及周期变化,然后通过“diff”函数对序列进行差分,使之成为零均值、无明显趋势变化的平稳序列。②模型识别:应用自相关系数函数图(ACF)、偏自相关系数函数图(PACF)分析序列特征(趋势性、季节性),并利用单位根检验方法(ADF)检验序列的平稳性。若序列平稳,进行平稳序列的时间序列分析; 若序列不平稳,结合本文序列特征,采用普通差分和季节性差分等合适的数据预处理方法,实现序列平稳化后进行分析。③参数估计:ARIMA乘积季节模型运用最大似然估计(maximum likelihoodestimation,MLE),根据p,d,q和P,D,Q的阶值计算出自回归和移动平均系数。④模型诊断:通过“Box.test”函数计算Box-Ljung统计量,如果统计量差异无统计学意义,可认为残差为自噪声,若残差序列不是自噪声,则需对模型进行改进。若残差序列满足自噪声过程,通过AIC等指标挑选最优模型,AIC越小,模型的拟合程度越好。此外,通过比较2015年1月—2017年12月实际发病率和模型拟合发病率,计算各月绝对误差和相对误差水平来评价模型的拟合效果。⑤模型预测:以上步骤建立2006年l月—2014年12月兰州市水相关疾病发病率模型,通过“forecast.Arima”函数模型预测2015年1月—2017年12月年发病率[5-6]。
1.4 统计学方法利用美国IBM公司SPSS 20.0统计软件建立数据库,运用R3.1.3中“tseries”和“forecast”软件包进行数据处理和建立模型。R软件是新西兰奥克兰大学的Robert Gentlman和RosS lhaka及其他志愿人员开发的免费统计分析软件,可用来探索数据、统计分析及做图等。
1.5 质量控制本研究兰州市水相关疾病发病数据来自全国传染病报告信息管理系统,平台资料完整,数据真实可靠。从平台导出的资料在录入计算机建立数据库时设置逻辑检查,并进行双重录入。
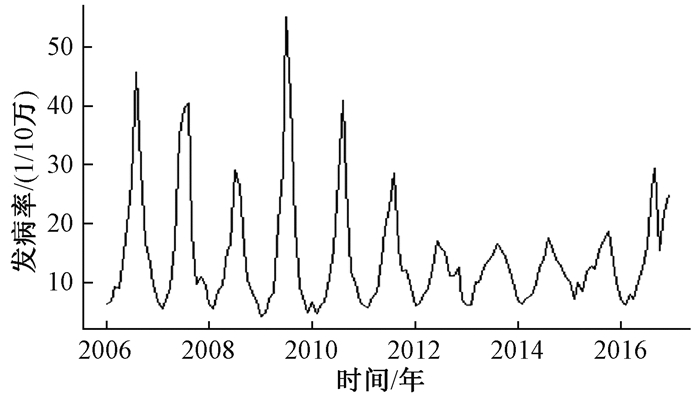
2 结果 2.1 水相关疾病月发病率情况结果显示:兰州市2006—2017年水相关疾病前期发病率高峰主要集中每年7—8月,2016—2017年秋冬季发病人数也比较多(表 1)。进一步应用“plot”函数绘制2006年—2017年兰州市水相关疾病月发病率的时间序列图,结果显示兰州市水相关疾病发病率为非平稳序列,呈一定的周期性和季节性趋势(图 1)。
| 月份/月 | 2006年 | 2007年 | 2008年 | 2009年 | 2010年 | 2011年 | 2012年 | 2013年 | 2014年 | 2015年 | 2016年 | 2017年 |
| 1 | 6.26 | 6.76 | 6.38 | 4.14 | 6.69 | 6.23 | 5.92 | 6.2 | 7.04 | 10.09 | 7.13 | 13.26 |
| 2 | 6.88 | 5.51 | 5.57 | 4.83 | 4.73 | 5.7 | 6.44 | 6.2 | 6.35 | 7.07 | 6.20 | 11.49 |
| 3 | 9.25 | 7.69 | 8.62 | 7.07 | 6.38 | 7.53 | 7.85 | 10.09 | 7.35 | 9.90 | 8.00 | 13.64 |
| 4 | 9.03 | 9.06 | 9.40 | 0.25 | 6.69 | 8.31 | 8.93 | 9.99 | 7.72 | 8.44 | 7.13 | 11.18 |
| 5 | 14.94 | 16.50 | 15.38 | 19.99 | 10.55 | 13.82 | 12.36 | 12.39 | 9.59 | 11.89 | 9.99 | 15.63 |
| 6 | 21.73 | 35.05 | 16.34 | 29.14 | 15.6 | 19.08 | 17.00 | 13.79 | 12.48 | 12.73 | 12.45 | 17.78 |
| 7 | 26.84 | 39.48 | 29.14 | 55.17 | 27.68 | 22.57 | 15.85 | 14.54 | 13.85 | 12.27 | 16.06 | 23.19 |
| 8 | 45.67 | 40.47 | 26.49 | 41.59 | 40.88 | 28.52 | 15.16 | 16.5 | 17.53 | 15.57 | 26.00 | 19.83 |
| 9 | 29.54 | 18.34 | 15.69 | 19.40 | 26.77 | 15.94 | 11.05 | 15.69 | 15.44 | 17.12 | 29.36 | 11.86 |
| 10 | 16.69 | 9.53 | 10.37 | 9.15 | 11.92 | 11.89 | 11.05 | 14.35 | 13.92 | 18.68 | 15.44 | 14.29 |
| 11 | 13.17 | 10.93 | 8.28 | 6.66 | 9.96 | 12.11 | 12.61 | 11.95 | 12.8 | 13.64 | 22.01 | 32.10 |
| 12 | 9.53 | 9.46 | 6.79 | 4.83 | 6.69 | 9.06 | 7.04 | 9.22 | 11.08 | 10.09 | 24.84 | 30.01 |
|
| 图 1 2006—2017年兰州市水相关疾病月发病情况 |
2.2 模型识别及构建
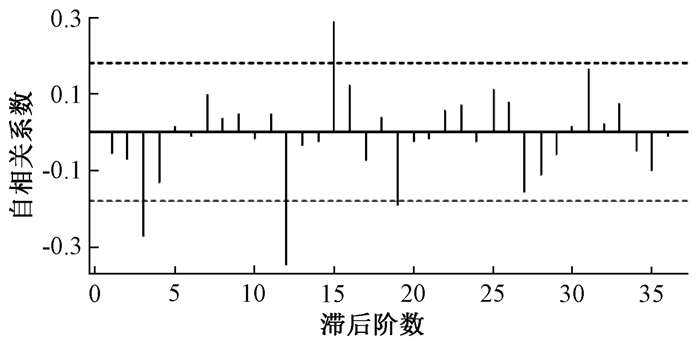
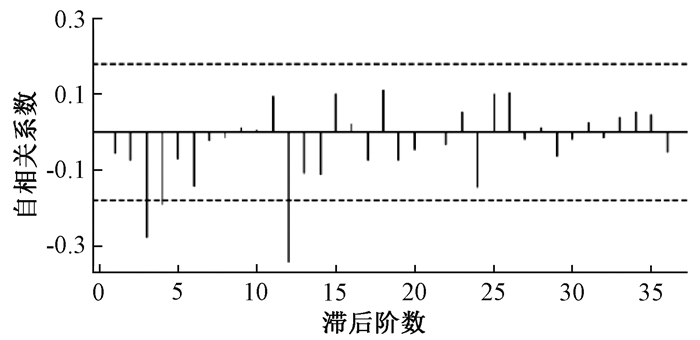
通过ADF检验后,2006年l月—2014年12月水相关疾病发病率ADF检验统计量为0.678,P=0.7647,该序列非平稳。对序列进行了1阶差分和1阶季节性差分后ADF检验统计量为-2.560,P < 0.001,序列满足平稳性要求,故非季节差分阶数d和季节差分阶数D均取1,季节性循环周期s定为12,详见图 2和3。最终确定模型为ARIMA(p,d,1) (P,0,0)12乘积季节模型。在此模型基础上借助参数检验和模型诊断,通过R软件的auto.arima函数得到推荐的最佳模型为ARIMA(2,0,1) × (2,0,0)12。
|
| 图 2 拆分后数据序列自相关分析图 |
|
| 图 3 拆分后数据序列偏自相关分析图 |
2.3 模型诊断
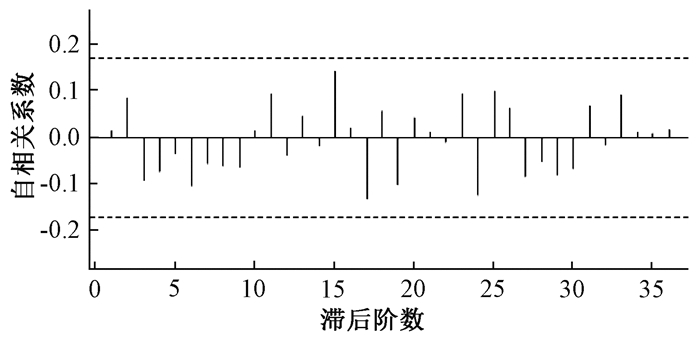
应用最大似然估计法对确定的模型进行参数估计,结果显示参数估计的结果差异均具有统计学意义(P < 0.05;表 2)。该模型的对数似然值为19.6,模型的标准误为0.046,AIC值=23.67,BIC值=14.23。结果显示:模型的残差为随机分布且自相关系数均在随机区间内,对模型的残差值计算Box-Ljung统计量检验,得出Q=18.64,P=0.824,认为模型残差为白噪声。可以确定建立的模型ARIMA(2,0,1)×(2,0,0)12是合适的。
| 参数 | 估计值 | 标准误 | t值 | P值 |
| ar1 | 1.658 5 | 0.074 5 | 5.967 | 0.000 |
| ar1 | -0.783 0 | 0.092 4 | -3.481 | 0.000 |
| ma1 | -0.765 3 | 0.122 0 | -6.137 | 0.000 |
| sar1 | 0.478 6 | 0.095 8 | 1.804 | 0.000 |
| sar2 | 0.267 1 | 0.136 0 | 1.673 | 0.000 |
2.4 模型的预测
用所建立的模型拟合并预测2015年1月— 2017年12月兰州市水相关疾病发病情况,计算其预测值和95%置信区间得到的预测下限及上限值(如表 3~表 5)。根据文献[6-7]提供的方法,一般认为平均相对误差不超过5%,且实际值都在拟合值的95%可信上限内,模型拟合效果较好。
| 月份/月 | 预测发病率/% | 95%可信区间 | 实际发病率/% | 绝对误差 | 相对误差 | |
| 下限 | 上限 | |||||
| 1 | 11.11 | 9.89 | 12.34 | 10.09 | 1.02 | 0.10 |
| 2 | 6.98 | 6.54 | 9.78 | 7.07 | -0.09 | -0.01 |
| 3 | 10.35 | 7.76 | 12.67 | 9.90 | 0.45 | 0.05 |
| 4 | 9.01 | 5.68 | 11.42 | 8.44 | 0.57 | 0.07 |
| 5 | 12.14 | 9.23 | 14.78 | 11.89 | 0.25 | 0.02 |
| 6 | 11.95 | 8.96 | 16.43 | 12.73 | -0.78 | -0.06 |
| 7 | 12.45 | 10.05 | 14.33 | 12.27 | 0.18 | 0.01 |
| 8 | 16.28 | 13.25 | 20.34 | 15.57 | 0.71 | 0.05 |
| 9 | 16.87 | 12.64 | 21.46 | 17.12 | -0.25 | -0.01 |
| 10 | 19.21 | 13.56 | 22.35 | 18.68 | 0.53 | 0.03 |
| 11 | 12.78 | 10.74 | 19.76 | 13.64 | -0.86 | -0.06 |
| 12 | 9.87 | 6.82 | 14.76 | 10.09 | -0.22 | -0.02 |
| 月份/月 | 预测发病率/% | 95%可信区间 | 实际发病率/% | 绝对误差 | 相对误差 | |
| 下限 | 上限 | |||||
| 1 | 7.32 | 4.58 | 10.26 | 7.13 | 0.19 | 0.03 |
| 2 | 5.97 | 3.54 | 9.89 | 6.20 | -0.23 | -0.04 |
| 3 | 7.77 | 4.23 | 11.74 | 8.00 | -0.23 | -0.03 |
| 4 | 7.57 | 5.02 | 10.87 | 7.13 | 0.44 | 0.06 |
| 5 | 10.26 | 7.38 | 13.08 | 9.99 | 0.27 | 0.03 |
| 6 | 13.01 | 7.76 | 16.86 | 12.45 | 0.56 | 0.04 |
| 7 | 15.89 | 10.05 | 18.45 | 16.06 | -0.17 | -0.01 |
| 8 | 27.03 | 18.54 | 31.06 | 26.00 | 1.03 | 0.04 |
| 9 | 29.69 | 22.34 | 32.37 | 29.36 | 0.33 | 0.01 |
| 10 | 15.89 | 12.64 | 20.55 | 15.44 | 0.45 | 0.03 |
| 11 | 21.87 | 16.74 | 24.69 | 22.01 | -0.14 | -0.01 |
| 12 | 23.96 | 18.52 | 27.89 | 24.84 | -0.88 | -0.04 |
| 月份/月 | 预测发病率/% | 95%可信区间 | 实际发病率/% | 绝对误差 | 相对误差 | |
| 下限 | 上限 | |||||
| 1 | 14.61 | 10.01 | 16.78 | 13.26 | 1.35 | 0.10 |
| 2 | 10.19 | 8.99 | 13.45 | 11.49 | -1.30 | 0.11 |
| 3 | 12.91 | 9.34 | 15.56 | 13.64 | -0.73 | -0.05 |
| 4 | 12.54 | 7.68 | 13.94 | 11.18 | 1.36 | 0.12 |
| 5 | 16.34 | 10.11 | 17.67 | 15.63 | 0.71 | 0.05 |
| 6 | 14.22 | 10.64 | 20.22 | 17.78 | -3.56 | -0.20 |
| 7 | 21.55 | 13.87 | 26.03 | 23.19 | -1.64 | -0.07 |
| 8 | 20.86 | 14.52 | 22.21 | 19.83 | 1.03 | 0.05 |
| 9 | 9.49 | 8.04 | 13.59 | 11.86 | -2.37 | -0.20 |
| 10 | 15.43 | 9.51 | 17.25 | 14.29 | 1.14 | 0.08 |
| 11 | 28.68 | 20.61 | 34.76 | 32.10 | -3.42 | -0.11 |
| 12 | 29.01 | 21.32 | 32.69 | 30.01 | -1.00 | -0.03 |
本研究预测值与实际值的平均相对误差为-0.05%,实际值都在95%的可信限之内,说明模型拟合效果较好。
|
| 图 4 模型残差的自相关分析图 |
3 讨论
水相关疾病是一类由细菌、病毒、原虫等多种病原体引起的、以腹泻为主的肠道传染病,是长期以来危害人民群众的常见病和多发病,由于该类疾病发病率高且流行极其广泛,可对居民生活以及医院医疗资源的配置都会产生明显影响。如果能够对其发病情况进行预测,将有助于适时开展居民健康干预工作,并提前合理调配卫生资源[6]。
由于水相关疾病包含疾病的种类太多,传统的回归方法以及指数平滑法等时间序列分析模型,要么由于因变量太多无法精确拟合,要么因滞后误差而影响预测精度,均不能很好的对其进行预测。与传统因果回归分析法相比,ARIMA乘积季节模型的建立并不需要将影响疾病发生的相关因素(包含未知因素)全部纳入,只需连续收集客观的时间序列就可建立较为稳定的模型,探讨其随时间发展变化规律并做外推预测。与传统时间序列模型相比,ARIMA乘积季节模型除提取强劲的确定性信息外,还能提取随机性信息,并能判断季节效应、趋势效应和随机波动等因素之间确切的作用关系[8-9]。本文运用ARIMA乘积季节模型,不仅较好地模拟了兰州市水相关疾病的流行态势,而且也较好地预测了未来的发病情况。
从本次调查数据来看,水相关疾病时间序列具有二重趋势变化的特点,即整体趋势变动性和季节波动性。运用ARIMA乘积季节模型,可以将各种因素包括未知因素的综合效应统一纳入到时间变量中,使模型更加简化。模型拟合结果也显示,ARIMA乘积季节模型的预测值与实际发病数据具有高度一致性,能够起到有效的预警作用。本文采用ARIMA乘积季节模型,通过分析水相关疾病的历史发病规律,构建ARIMA(2,0,1)×(2,0,0)12模型乘积季节模型,该模型可对兰州市水相关疾病疫情的监测预警和预防控制工作提供科学的理论依据。为了提高模型的适用性,需通过积累新的周期数据对ARIMA模型进行修正和重新拟合,提高模型的预测应用能力。水相关疾病的发病受到气象条件、个人卫生习惯等与疾病传播有关的一些随机因素的的影响,同时也受到水源性因素和食源性因素的区分界定等因素干扰。因此在水相关疾病的预测防控中应提高病原诊断信息报告率和报告质量,将有助于公共卫生人员进一步利用报告信息,开展预测和预警,有效预防水相关疾病的发生。
| [1] |
金银龙. GB 5749-2006《生活饮用水卫生标准》释义[M]. 北京: 中国标准出版社, 2007: 10, 13, 16.
|
| [2] |
何晓燕, 李苑, 黄志平, 等. 应用ARIMA模型预测宝安区某街道其它感染性腹泻发病率的探讨[J]. 现代生物医学进展, 2011, 11(16): 3138-3142. (In English: He XY, Li Y, Huang ZP, et al. Exploration of the incidences of other infectious diarrheas at a township, Bao'an district predicted by ARIMA model[J]. Prog Mod Biomed, 2011, 11(16): 3138-3142.) |
| [3] |
吴昊澄, 徐旭卿, 王臻, 等. 浙江省细菌性痢疾月发病率ARIMA模型建立及预测分析[J]. 浙江预防医学, 2012, 24(1): 14-16. (In English: Wu HC, Xu XQ, Wang Z, et al. Application of ARIMA model for estimating the incidence of bacillary dysentery[J]. Zhejiang Prev Med, 2012, 24(1): 14-16. DOI:10.3969/j.issn.1007-0931.2012.01.004) |
| [4] |
胡建利, 刘文东, 梁祁, 等. 季节指数法和ARIMA模型在感染性腹泻周发病数预测中的应用研究[J]. 中华疾病控制杂志, 2013, 17(8): 718-721. (In English: Hu JL, Liu WD, Liang Q, et al. Applications of season index method and ARIMA model on weekly prediction of infectious diarrhea incidence[J]. Chin J Dis Control Prev, 2013, 17(8): 718-721.) |
| [5] |
陈磊, 徐建辉, 高丽. 基于ARIMA模型的象山半岛水性疾病时间序列分析[J]. 浙江预防医学, 2015, 27(11): 1131-1133. |
| [6] |
刘峰, 朱妮, 邱琳, 等. ARIMA乘积季节模型在陕西省手足口病预测中的应用[J]. 中华流行病学杂志, 2016, 37(8): 1117-1120. (In English: Liu F, Zhu N, Qiu L, et al. Application of R-based multiple seasonal ARIMA model, in predicting the incidence of hand, foot and mouth disease in Shaanxi province[J]. Chin J Epidemiol, 2016, 37(8): 1117-1120. DOI:10.3760/cma.j.issn.0254-6450.2016.08.013) |
| [7] |
李峰, 陈胤忠, 徐士林, 等. ARIMA乘积季节模型在盐城市手足口病疫情预测中的应用[J]. 疾病监测, 2016, 31(10): 864-869. (In English: Li F, Chen YZ, Xu SL, et al. Application of ARIMA product seasonal model in predicting incidence of hand foot and mouth disease in Yancheng[J]. Dis Surveill, 2016, 31(10): 864-869. DOI:10.3784/j.issn.1003-9961.2016.10.015) |
| [8] |
马晓梅, 刘颖, 杨梦利, 等. 手足口病月发病率ARIMA乘积季节模型预测探讨[J]. 现代预防医学, 2017, 44(9): 1541-1544, 1560. (In English: Ma XM, Liu Y, Yang ML, et al. Multiple seasonal ARIMA model in prediction of the monthly incidence of the hand-foot-mouth disease[J]. Mod Prev Med, 2017, 44(9): 1541-1544, 1560.) |
| [9] |
王建书, 刘强, 覃江纯, 等. 基于ARIMA乘积季节模型的苏州市介水传染病发病预测研究[J]. 环境卫生学杂志, 2017, 7(6): 417-420. (In English: Wang JS, Liu Q, Qin JC, et al. Prediction of incidence for water-borne diseases on a multiple seasonal ARIMA model in Suzhou[J]. Journal of Environmental Hygiene, 2017, 7(6): 417-420.) |


