2. 四川大学;
3. 深圳市妇幼保健院
深圳市作为中国改革开放的前沿城市,经济发展迅速、人口密集程度高,该地区大气污染问题逐渐引起人们的普遍关注,目前已有许多学者针对深圳的空气质量状况展开了广泛的研究[1-5]。目前在评估深圳空气质量时间分布时,存在一些不足之处:① 选择的评价指标缺乏代表性。目前大多数文献研究指标主要选择常规污染物如:细颗粒物(PM2.5)、可吸入颗粒物(PM10)等或空气污染指数(API),很少利用综合性指标如空气质量指数(AQI)进行评价。2012年国家颁布实施的《环境空气质量标准》(GB 3095-2012)[6],对应的空气质量评价体系由API变成了AQI,在API的基础上增加了PM2.5、臭氧(O3)、一氧化碳(CO)3种污染物指标,发布频次也从每天一次变成每小时一次。② 选择的研究方法欠佳。环境大气污染预测方法主要有数值模式方法和统计方法两种。由于数值模式方法需要较详尽的源强时空分布资料和分辨率很高的气象模式,因此对现阶段我国大多数城市而言,发展数值预测模式并不成熟。对大气污染物进行统计预测应用较为广泛,主要采用灰色预测模型[7]、神经网络预测模型[8]等预测方法。应用较广泛的是神经网络预测模型,他是拟合非线性现象的强有力工具,但其具有易陷入局部最优、过拟合、很难确定网络结构等问题,影响预测模型的泛化能力。自回归移动平均模型(ARIMA)属于统计学范畴,通过研究、分析和处理时间序列,提取出系统的相关信息,从而揭示时间序列本身的结构与规律,挖掘系统的固有特性,掌握系统与外界的联系,推断出系统的未来变化趋势,已演变为一种系统分析的研究方法。
本研究基于深圳市2014年1月1日—2016年6月30日AQI日报数据,利用时间序列分析方法中的ARIMA模型模拟深圳市空气污染的时间变化特征,并利用2016年7月1日—2016年7月6日深圳市AQI日报数据对ARIMA模型进行预测效果评价,为有效地治理和控制深圳市空气污染提供科学依据。
1 材料与方法 1.1 数据来源本研究收集的深圳市逐日AQI数据均来源于http://datacenter.mep.gov.cn/(中华人民共和国环境保护部数据中心),选取2014年1月1日—2016年6月30日912个逐日AQI数据构建ARIMA模型,利用该模型预测深圳市2016年7月1日—2016年7月6日AQI数据并进行预测效果评价。
1.2 研究方法 1.2.1 建模原理ARIMA模型是由Box和Jenkings于20世纪70年代初提出的著名时间序列预测方法,其基本公式如(1),该方法可以用时间序列的过去值预测未来值[9]。ARIMA(p,d,q)称为差分自回归移动平均模型。
| $ \begin{gathered} {\text{X}}\left( {\text{t}} \right) = {{\mathtt{φ }}_1}{{\text{X}}_{\left( {{\text{t}} - 1} \right)}} + {{\mathtt{φ }}_2}{{\text{X}}_{\left( {{\text{t}} - 2} \right)}} + ... + {{\mathtt{φ }}_{\text{p}}}{{\text{X}}_{\left( {{\text{t}} - {\text{p}}} \right)}} + {{\text{e}}_{\left( {\text{t}} \right)}} - \hfill \\ {{\mathtt{θ }}_2}{{\text{e}}_{\left( {{\text{t}} - 2} \right)}} - ...{{\mathtt{θ }}_{\text{q}}}{{\text{e}}_{\left( {{\text{t}} - {\text{q}}} \right)}} \hfill \\ \end{gathered} $ | (1) |
式中:p—自回归模型的阶数;
φp—自回归模型的系数;
q—滑动平均模型的阶数;
θq—模型滑动平均系数;
X(t)—时间序列在t时刻的预测值;
X(t-1)—时间序列在t-i时刻的观测值;
e(t-1)—时间序列模型在t-i时刻的误差或偏差[10]。
ARIMA模型的基本思路是将预测对象随时间的推移和变动所形成的数据序列看成是随机序列,然后再用合适的数学模型来近似地模拟和描述该序列。一旦合适的时间序列模型建立成功,就可利用该时间序列的所有己知值来预测想要获得的未知值[11]。
1.2.2 建模流程 1.2.2.1 数据预处理ARIMA模型建模方法是以序列平稳性为前提,因此首先应判断原序列是否平稳,若为非平稳序列则进行数据的平稳化处理,对原始数据进行对数转换或者差分,使序列平稳后再构建ARIMA模型。
1.2.2.2 模型识别ARIMA模型分为自回归模型、移动平均模型和自回归求和移动平均模型即AR(p)、MA(q)和ARIMA(p,d,q)模型,其中p,d,q分别表示时间序列的自回归阶数、差分阶数和移动平均阶数。如果时间序列存在季节性周期波动,则需采用季节性ARIMA模型,可标记为ARIMA(p,d,q)(P,D,Q)S,P,D,Q,s分别表示季节自回归阶数,季节差分阶数,季节移动平均阶数和循环周期长度。利用自相关分析和偏相关分析,依据AIC(赤池信息准则)和BIC(贝叶斯信息准则)确定模型的阶数,选择AIC和BIC值最小的模型为最佳模型[12]。
1.2.2.3 参数估计根据变换后平稳时间序列的自相关和偏自相关图,估计模型的p、P、q、Q值,采用最大似然估计或最小二乘法估计等对初步估计模型进行检验。
1.2.2.4 模型检验模型检验主要是检验模型对原时间序列的拟和效果,就是检验整个模型对信息的提取是否充分,即检验残差序列是否为白噪声序列。如果拟合模型通不过检验,即残差序列不是白噪声序列,那么要重新选择模型进行拟合。如残差序列是白噪声序列,就认为拟合模型是有效的。模型的有效性检验仍然是使用上述Q统计量对残差序列进行卡方检验。
1.2.2.5 模型预测采用本研究构建的最佳ARIMA模型对2016年7月1日—2016年7月6日AQI数值进行预测,与2016年7月1日—2016年7月6日实际AQI数值进行比较。并用相对预测误差(|实际AQI值-预测AQI值|/实际AQI值)来评价模型的预测效果。
1.3 统计分析本研究采用Excel 2010对数据进行整理,利用R 3.3.1软件进行时间序列建模和预测。
2 结果 2.1 空气质量级别与首要污染物本研究共收集了深圳市912天逐日AQI数据,按照《环境空气质量标准》(GB 3095-2012)[6]评价发现,空气质量级别为优、良和轻度污染的比例分别是48.6%、48.4%和3.0%,优良级别在96%以上(表 1);AQI是各项污染物的空气质量分指数(IAQI)中的最大值,当AQI大于50时对应的污染物即为首要污染物,若IAQI最大的污染物为两项或两项以上时,并列为首要污染物。2014年PM2.5作为首要污染物占百分比最高(25.8%),2015年O3作为首要污染物占百分比最高(19.7%),2016年O3作为首要污染物占百分比最高(17.6%;表 2)。
| 空气质 量级别 |
2014年 | 2015年 | 2016年 | 合计 | |||||||
| 天数/d | 百分比/% | 天数/d | 百分比/% | 天数/d | 百分比/% | 天数/d | 百分比/% | ||||
| 优 | 159 | 43.6 | 185 | 50.7 | 100 | 54.9 | 444 | 48.6 | |||
| 良 | 192 | 52.6 | 169 | 46.3 | 80 | 44.0 | 441 | 48.4 | |||
| 轻度污染 | 14 | 3.8 | 11 | 3.0 | 2 | 1.1 | 27 | 3.0 | |||
| 合计 | 365 | 100.0 | 365 | 100.0 | 182 | 100.0 | 912 | 100.0 | |||
| 首要 污染物 |
2014年 | 2015年 | 2016年 | 合计 | |||||||
| 天数/d | 百分比/% | 天数/d | 百分比/% | 天数/d | 百分比/% | 天数/d | 百分比/% | ||||
| NO2 | 34 | 9.3 | 32 | 8.8 | 29 | 15.9 | 95 | 10.4 | |||
| PM10 | 43 | 11.8 | 54 | 14.8 | 8 | 4.4 | 105 | 11.5 | |||
| PM2.5 | 94 | 25.8 | 30 | 8.2 | 15 | 8.2 | 139 | 15.2 | |||
| O3 | 44 | 12.1 | 72 | 19.7 | 32 | 17.6 | 148 | 16.2 | |||
2.2 空气质量趋势分析
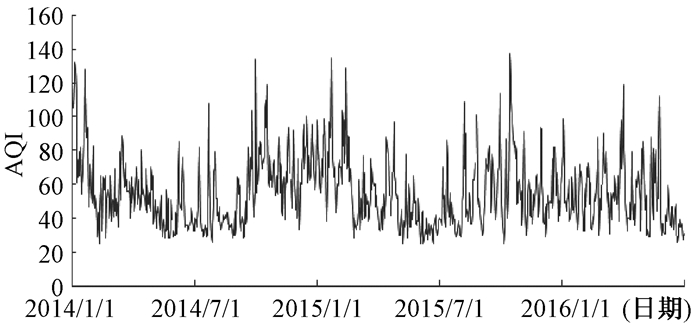
绘制深圳市2014年1月1日—2016年6月30日逐日AQI时间序列图(图 1),发现每年AQI变化趋势呈“U”型分布,表现为春、冬季节高,夏、秋季节低的趋势。但从整体上看,2014年—2016年深圳市AQI年均值基本持平。
|
| 图 1 深圳市2014年—2016年逐日AQI时间序列图AQI |
2.3 构建ARIMA模型 2.3.1 序列平稳性检验
经ADF单位根检验发现,Dickey-Fuller=-5.9692,P=0.01,再结合AQI时间序列图(图 1)可以说明该时间序列确实是平稳的,不存在单根问题,因此ARIMA模型中的参数d=0。
2.3.2 模型识别本研究采用R软件forecast程序包中ARIMA自动拟合函数即auto. arima(函数)进行拟合,该函数基于AIC或BIC,进行逐步筛选,并结合时间序列自相关和偏自相关图来选择合适的模型。
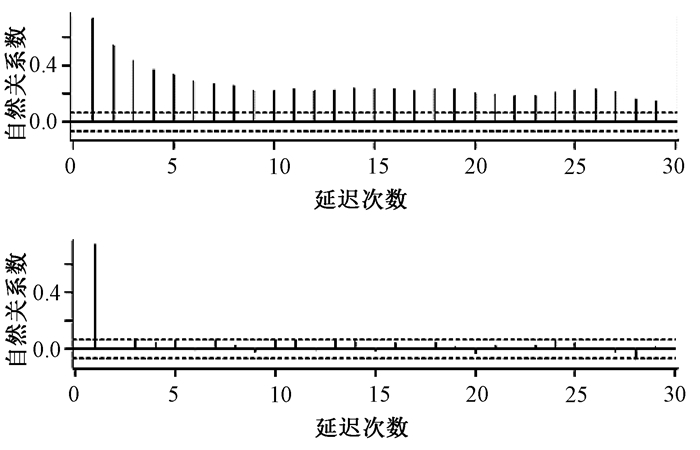
绘制时间序列自相关和偏相关分析图(图 2),发现ACF拖尾,PACF1步截尾(P=1),再结合auto. arima(函数),利用AIC和BIC最小准则,结果显示ARIMA(3,0,1) 模型的AIC和BIC最小,其分别为7 364.51和7 393.41,因此可以用ARIMA(3,0,1) 对深圳市AQI时间序列进行拟合,其表达式为:
| $ \begin{gathered} {{\text{X}}_{{\text{(t)}}}}{\text{ = 53}}{\text{.2189 + 1}}{\text{.6387}}{{\text{X}}_{{\text{(t-1)}}}}{\text{-0}}{\text{.7076}}{{\text{X}}_{{\text{(t-2)}}}} \hfill \\ {\text{ + 0}}{\text{.0613}}{{\text{X}}_{{\text{(t - 3)}}}}{\text{ + }}{{\text{e}}_{{\text{(t)}}}}{\text{ + 0}}{\text{.9311}}{{\text{e}}_{{\text{(t - 1)}}}} \hfill \\ \end{gathered} $ |
|
| 图 2 AQI时间序列自相关和偏相关分析图 |
2.3.3 模型验证
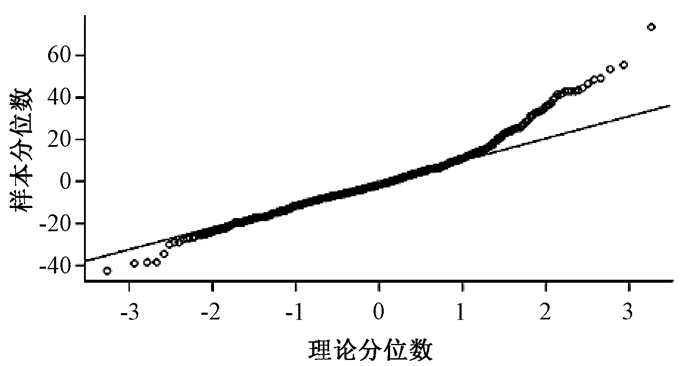
一个合适的模型,其残差应该满足均值为0的正态分布,并且对于任意的滞后阶数,残差自相关系数都应该为零。本研究采用qqnorm(输出)(图 3)。如果数据满足正态分布,则数据中的点会落在qqnorm图中的线上。显然本研究结果符合上述要求。
|
| 图 3 arima(3, 0, 1) 模型残差正态Q-Q图 |
进一步利用Box.test(函数检验)ARIMA(3,0,1) 模型残差的自相关系数是否都为零,结果发现:残差围绕0上下波动,并且没有明显的自相关性,进行Ljung-Box测试显示:所有P>0.05,说明模型残差为白噪声,所建立的模型是合适的,可以用于预测研究。
2.4 模型预测运用R软件forecast包中forecast.arima(命令),用ARIMA(3,0,1) 模型对深圳市2016年7月1日—2016年7月6日,6天的AQI数值进行预测。
利用模型预测值与实际监测值进行对比分析发现,利用ARIMA(3,0,1) 模型对深圳市AQI数值进行预测的绝对误差在[0~8]之内,相对预测误差 < 30%,其平均相对预测误差为16.6%,详细预测结果见表 3。由此可知,预测精度是较为理想的。
| 日期 | AQI 实际值 |
AQI 预测值 |
误差值 | 相对预测 误差/% |
| 2016/7/1 | 26 | 31.175 59 | 5.175 59 | 19.9 |
| 2016/7/2 | 26 | 31.998 52 | 5.998 52 | 23.1 |
| 2016/7/3 | 25 | 32.032 87 | 7.032 87 | 28.1 |
| 2016/7/4 | 28 | 32.794 87 | 4.794 87 | 17.1 |
| 2016/7/5 | 30 | 33.502 19 | 3.502 19 | 11.7 |
| 2016/7/6 | 37 | 39.045 98 | 2.045 98 | 5.5 |
3 讨论
本研究中发现2014年—2016年深圳市每年逐日AQI变化趋势呈“U”型分布,与其他城市[13-15]类似,表现为夏秋季空气质量较好,冬春季空气质量较差。其可能原因是深圳夏秋季盛行的西南季风挟带来海面上的清洁空气,加之降雨频繁,有利于污染物的沉降,此时空气质量较好;冬春季盛行东北季风,带来内陆的污染气团,加之大气混合层高度较低,导致空气质量较差,此时外地传输与本地排放都有重要作用。因此深圳大气污染具有鲜明的季节特征,有研究也证明了这一趋势[4-5]。
2014年—2016年深圳市AQI < 100(即空气质量优秀或良好)占每年有效观察天数的百分比分别为96.2%、97.0%和98.9%,其明显高于国内其他城市[16]。综合以上分析认为深圳市空气质量状况较好并且逐年有所好转。深圳市2011年全年本地生产总值11 515.86亿元上升到2015年全年本地生产总值17 502.99亿元,经济保持高速增长而空气质量逐年改善,这可能与深圳市产业结构调整转变,经济增长方式改革有关。如2015年深圳市第一产业比重下降1.7%,其增加值占全市生产总值的比重不到0.1%;第二、三产业分别增长7.3%、10.2%,第二、三产业增加值占全市生产总值的比重分别为41.2%和58.8%[17]。另外,深圳环境立法工作稳步推进(如:《深圳经济特区机动车排气污染防治条例》、《深圳市扬尘污染防治管理办法》等法规),并实施了强化重点污染源的监管和整治、全面推进机动车和远洋船舶尾气污染防治工作、深入开展“蓝天行动”(工业减排、燃烧减量、消烟除尘、尾气达标、扬尘管控)等措施,说明以上治理措施对治理该市大气污染起到了重要作用。
大气环境的污染源分为固定污染源和流动污染源两类,固定污染源主要来自工业和居民生活的排气污染,流动污染源主要来自机动车尾气的排放,CO、NO2和NOx是比较明确的汽车尾气排放物[18]。深圳大气污染源解析发现深圳的各类污染源中,机动车尾气排放为主要来源,占深圳PM2.5本地排放源的41%,其次为工业挥发性有机化合物转化及其他工业过程、扬尘、远洋船、电厂、海洋和生物质燃烧,分别占15%、12%和11%、8%、5%、3%[19]。2014年底深圳市机动车保有量超过314万辆,近5年年均增长率约16%,说明近年交通源污染已成为深圳市区主要空气污染源之一。进一步分析发现2014年PM2.5作为首要污染物出现频率最高(25.8%),2015年O3作为首要污染物出现频率最高(19.7%),2016年O3作为首要污染物出现频率最高(17.6%),这一现象与国内其他城市[14]略有不同,可见近年来深圳O3污染越来越明显。臭氧污染主要是一种光化学反应,汽车尾气、工厂烟雾等排入大气的挥发性有机污染物(VOCs)和氮氧化物,在强烈的阳光紫外线照射下,经过光化学反应,产生了臭氧等有毒气体。现有研究发现深圳市O3污染处于VOCs控制区,为更有效控制O3污染,除了控制NOx水平外,还应加大VOCs污染控制[20]。然而由于VOCs污染源分布零散、行业众多,监管难度极大,深圳市VOCs污染治理尚处于起步阶段。因此在未来需要全面强有力的VOCs控制措施,大幅提高VOCs削减比例,才能有效制约臭氧污染。因此深圳市在控制空气污染时除了关注空气中PM2.5水平,同时O3污染水平还应引起重视。
ARIMA模型是目前应用较多的时间序列预测方法之一,其优势在于可以将多种影响因素综合效应蕴含于时间变量中,通过综合考虑序列的趋势变化、周期变化和随机干扰并借助统计模型进行量化表达,且可以通过反复识别及修改以获得更为满意的模型[21]。ARIMA模型是一种实用性强、精确度高的短期预测方法[22],近年来国内学者利用ARIMA模型在空气污染指数(API)[23]、NOx、SOx和PM10[24]和PM2.5[25]等预测中进行了成功运用。本研究运用R语言采用ARIMA模型对深圳市2014年—2016年AQI平稳序列的时间序列建模。再对数据先后尝试了自相关、偏相关分析和auto.arima(函数自动筛选分析),最终得到了模型的最优拟合模型ARIMA(3, 0, 1)。研究中进一步利用ARIMA(3, 0, 1) 模型对2016年7月1日—2016年7月6日6天的AQI数值进行了预测,预测值与实际值的平均相对误差为16.6%,拟合较好,通过逐日AQI变化趋势图可以直观、清楚得看出模型的拟合情况以及未来6天深圳市AQI走向趋势。通过对ARIMA模型分析,表明应用时间序列分析深圳市空气质量状况是比较有效可行的。深圳市大气污染无论是长期趋势还是季节变动都有其自身的特点和规律性,发现这些规律可以有针对性地开展环境保护和治理工作。
每一种统计分析拟合方法并不是十全十美的,ARIMA模型也不例外。本研究采用的ARIMA拟合AQI趋势并进行预测中存在一些不足:① 时间序列ARMA模型所描述的是时间序列的自相关性和自身的动态记忆性,反映的是时间序列的短期变化关系,而不是长期变化关系。因此利用时间序列模型只能进行短期预测,在进行长时间预测时结果不稳定[26];本文运用ARIMA模型对深圳市AQI动态数据进行了拟合,并分析得到了适合深圳AQI的模型:ARIMA(3, 0, 1),并能进行了短期良好的预测(6 d),但不能实现较长时间的预测,在短期预测方面可以为相关部门提供参考依据;② ARIMA模型是精度较高的短期预测模型,随着预测时间的推移,预测精度会降低,因此一次分析提出的预测模型不能作为长期不变的预测依据,对已建立的ARIMA(3, 0, 1) 模型,需用新的AQI数据来验证,当预测精度达不到要求时,应修正或重新拟合更能反映实际的预测模型,以及时正确掌握空气质量变化趋势;③ ARIMA预测方法存在着一定的不确定性和误差,主要是因为该模型为时间序列数学模型,其应用在模拟AQI变化趋势上,主要反映了时间因素与AQI之间的联系,但影响城市空气质量变化的因素较多,如:气象条件、大气污染物排放等,这些因素具有一定的波动性,在时间尺度上分布可能存在不均衡性,从而会影响模型的拟合精度。因此基于以上不足之处,可结合非线性动力学方法等对其进行改进[27],这将是下一步研究方向。
| [1] | 谭德生, 陈军苗. 2004-2009年深圳空气质量及其污染物扩散条件分析[J]. 南昌大学学报(理科版), 2012, 36(3): 301–306. Tan DS, Chen JM. Analyse of air quality and diffusive conditions of contaminant in Shenzhen from 2004 to 2009[J]. Journal of Nanchang University (Natural Science), 2012, 36(3): 301–306. (in Chinese). |
| [2] | 杨红龙, 李磊, 饶华炎, 等. 深圳大运会期间车辆限行对空气污染物浓度的影响[J]. 环境与健康杂志, 2012, 29(8): 718–721. Yang HL, Li L, Rao HY, et al. Influence of traffic restriction on air quality during the 2011 Universiade in Shenzhen[J]. Journal of Environment and Health, 2012, 29(8): 718–721. (in Chinese). |
| [3] | 黄杰华, 何龙, 梁鸿, 等. 深圳发展对环境空气的影响评价[J]. 中国人口·资源与环境, 2016, 26(5): 58–61. |
| [4] | 余淑苑, 刘国红, 程锦泉, 等. 2002-2005年深圳市空气污染物浓度的动态分析[J]. 环境与健康杂志, 2006, 23(6): 512–514. Yu SY, Liu GH, Cheng JQ, et al. Air pollutants change in Shenzhen, China in 2002-2005[J]. Journal of Environment and Health, 2006, 23(6): 512–514. (in Chinese). |
| [5] | 张振, 余淑苑, 彭朝琼, 等. 深圳市2006-2010年空气污染物浓度变化特征[J]. 环境卫生学杂志, 2011, 1(6): 19–22. Zhang Z, Yu SY, Peng CQ, et al. The changing trend of air pollutants in Shenzhen, China in 2006-2010[J]. Journal of Environmental Hygiene, 2011, 1(6): 19–22. (in Chinese). |
| [6] | 中华人民共和国国家质量监督检验检疫总局, 中国国家标准化管理委员会. GB 3095-2012环境空气质量标准[S]. 北京: 中国标准出版社, 2016. General Administration of Quality Supervision, Inspection and Quarantine of the People's Republic of China, Standardization Administration of the People's Republic of China. GB 3095-2012 Ambient air quality standard[S]. Beijing:Standards Press of China, 2016. |
| [7] | 徐卫国, 田伟利, 张清宇, 等. 灰色关联分析模型在环境空气质量评价中的修正及应用研究[J]. 中国环境监测, 2006, 22(3): 63–66. Xu WG, Tian WL, Zhang QY, et al. Study on modification and application of grey relation analysis model in evaluation of atmospheric environmental quality[J]. Environmental Monitoring in China, 2006, 22(3): 63–66. (in Chinese). |
| [8] | 白鹤鸣, 沈润平, 师华定, 等. 基于BP神经网络的空气污染指数预测模型研究[J]. 环境科学与技术, 2013, 36(3): 186–189. Bai HM, Shen RP, Shi HD, et al. Forecasting model of air pollution index based on BP neural network[J]. Environmental Science & Technology, 2013, 36(3): 186–189. (in Chinese). |
| [9] | 王燕. 应用时间序列分析[M]. 北京: 中国人民大学出版社, 2006: 146-147. |
| [10] | Wolfson LJ, Grais RF, Luquero FJ, et al. Estimates of measles case fatality ratios:a comprehensive review of community-based studies[J]. Int J Epidemiol, 2009, 38(1): 192–205. doi: 10.1093/ije/dyn224 |
| [11] | 陶杰. 武汉市AQI与经济发展状况关系探究及预测[D]. 武汉: 华中师范大学, 2015. Tao J. The relationship of AQI and economic development in Wuhan, and the forecasting of AQI[D]. Wuhan:Central China Normal University, 2015. |
| [12] | 李燕婷, 张宏伟, 任宏, 等. 上海市流感样病例发病趋势的时间序列分析和预测模型研究[J]. 中华预防医学杂志, 2007, 41(6): 496–498. Li YT, Zhang HW, Ren H, et al. Application of time series analysis in the prediction of incidence trend of influenza-like illness in Shanghai[J]. Chinese Journal of Preventive Medicine, 2007, 41(6): 496–498. (in Chinese). |
| [13] | 柳笑盈. 基于GIS的空气质量指数空间插值方法研究[D]. 昆明: 昆明理工大学, 2015. |
| [14] | 冯建社, 张婷, 张明月, 等. 秦皇岛市空气质量指数AQI现状分析[J]. 中国环境管理干部学院学报, 2014, 24(5): 65–69. Feng JS, Zhang T, Zhang MY, et al. Status analysis on air quality index (AQI) in Qinhuangdao[J]. Journal of Environmental Management College of China, 2014, 24(5): 65–69. (in Chinese). |
| [15] | 王静, 朱翠翠, 李菲菲, 等. 基于AQI对京津冀地区空气污染的计量分析[J]. 牡丹江师范学院学报(自然科学版), 2016(1): 3–6. |
| [16] | 万莉鑫. 大数据背景下气象因素与AQI之间关系的实证分析[D]. 北京: 首都经济贸易大学, 2016. |
| [17] | 深圳市统计局. 2015年深圳国民经济和社会发展统计公报[R/OL]. 深圳统计, (2016-04-26). [2016-12-22]. http://www.sztj.gov.cn/xxgk/tjsj/tjgb/201604/t20160426_3606261.htm. |
| [18] | 陈瑞, 杨海霞, 蔡美. 2014年-2015年兰州市环境空气质量分析[J]. 环境卫生学杂志, 2016, 6(5): 324–327. Chen R, Yang HX, Cai M. Environmental air quality in Lanzhou city in 2014-2015[J]. Journal of Environmental Hygiene, 2016, 6(5): 324–327. (in Chinese). |
| [19] | 骆倩雯. 北杭广深首要大气污染源为机动车[N]. 北京日报, 2015-04-02(002). |
| [20] | 梁永贤, 尹魁浩, 胡泳涛, 等. 深圳地区臭氧污染来源的敏感性分析[J]. 中国环境科学, 2014, 34(6): 1390–1396. Liang YX, Yin KH, Hu YT, et al. Sensitivity analysis of ozone precursor emission in Shenzhen, China[J]. China Environmental Science, 2014, 34(6): 1390–1396. (in Chinese). |
| [21] | 范引光, 吕金伟, 戴色莺, 等. ARIMA模型与灰色预测模型GM(1, 1) 在HIV感染人数预测中的应用[J]. 中华疾病控制杂志, 2012, 16(12): 1100–1103. Fan YG, Lv JW, Dai SY, et al. Prediction on the number of HIV with models of ARIMA and GM (1, 1)[J]. Chinese Journal of Disease Control & Prevention, 2012, 16(12): 1100–1103. (in Chinese). |
| [22] | Daniels MJ, Dominici F, Samet JM, et al. Estimating particulate matter-mortality dose-response curves and threshold levels:an analysis of daily time-series for the 20 largest US cities[J]. Am J Epidemiol, 2000, 152(5): 397–406. doi: 10.1093/aje/152.5.397 |
| [23] | 孟凡强. ARIMA模型在空气污染指数预测中的应用[J]. 统计与决策, 2009(7): 33–35. |
| [24] | 卢虎生, 甄建静. SOx、NOx、PM10浓度的时间序列模型及其残差T2控制图[J]. 科技经济市场, 2015(5): 78–80. |
| [25] | 彭斯俊, 沈加超, 朱雪. 基于ARIMA模型的PM2.5预测[J]. 安全与环境工程, 2014, 21(6): 125–128. Peng SJ, Shen JC, Zhu X. Forecast of PM2.5 basedon the ARIMA model[J]. Safety and Environmental Engineering, 2014, 21(6): 125–128. (in Chinese). |
| [26] | 程文娜. PM10浓度的时间序列模型及预测[J]. 科学技术与工程, 2010, 10(9): 2260–2262, 2266. Cheng WN. Time series model and prediction of PM10 concentration[J]. Science Technology and Engineering, 2010, 10(9): 2260–2262, 2266. (in Chinese). |
| [27] | Chelani AB, Devotta S. Prediction of ambient carbon monoxide concentration using nonlinear time series analysis technique[J]. Transp Res D, 2007, 12(8): 596–600. doi: 10.1016/j.trd.2007.07.006 |

