2. 深圳市清时捷科技有限公司
亚硝酸盐氮是水体中含氮有机物进一步氧化,进行硝化过程的中间产物。饮用水中亚硝酸盐氮含量过高时,可使得人类肝癌、食道癌、胃癌的患病率增高,并损害人体心血管系统。我国《生活饮用水卫生标准》(GB 5749-2006)附录A[1]中规定饮水中亚硝酸盐的含量不得超过1 mg/L,即亚硝酸盐氮的含量不得超过0.3 mg/L。
依据《生活饮用水标准检验方法》(GB/T 5750-2006)[2],我国检验生活饮用水中亚硝酸盐氮的标准方法为重氮偶合分光光度法,与氨基苯磺酰胺重氮偶合后,采用分光光度计比色定量。一般分光光度计操作较为繁琐,配制试剂过程十分复杂,所需的水样和化学试剂用量大。因此,基于微型光学模块、微量比色池及自动进样系统,研制了一套集自动进样、自动计算结果、自动清洗于一体的新型微量自动分析仪及其配套的分析试剂盒,并建立了饮用水中亚硝酸盐氮的新型微量分光光度分析方法。该方法操作方便、维护简单,产生的废水废液少,减少了98%的样品用量及95%的化学试剂用量[3],适合一些经济欠发达地区或村镇地区的基层实验室。为了进一步考察该法测量结果的重现性和准确度,完善该方法的质量控制,并对测量结果及其质量进行评定、表示和比较,本文建立了新型微量分光光度法测定饮用水中的亚硝酸盐氮不确定度的评定方法,并分析了测量结果不确定度的来源及其分量大小,以此评估微量分光光度法测定饮用水中亚硝酸盐氮检测结果的有效性及影响测定结果的主要因素,为测量的质量控制提供科学依据,为一些经济欠发达地区或村镇地区的基层实验室使用该方法提供更科学的技术支持。
1 测定方法 1.1 仪器与试剂微量自动分析仪(课题组研发,中国);亚硝酸盐氮仪器分析试剂盒(课题组研发,批号:201308A):试剂R1:把1包R1-A倒入R1-B中溶解后使用;其中R1-A为磺胺等固体,R1-B为溶解液。亚硝酸盐氮标准物质[GBW (E)080223,ρ(NO2-N)=100 μg/mL (以N计),相对扩展不确定度2%],由国家标准物质中心提供。
1.2 标准系列的配制 1.2.1 配制亚硝酸盐氮标准溶液吸取1.00 mL亚硝酸盐氮标准储备液,用纯水定容至100 mL,得到浓度为1 mg/L的亚硝酸盐氮标准溶液。
1.2.2 制备亚硝酸盐氮标准系列分别吸取0 mL、0.10 mL、1.00 mL、6.00 mL、12.00 mL、20.00 mL亚硝酸盐氮标准使用液(1 mg/L)于6个100 mL容量瓶中,用纯水定容至100 mL,得到标准系列的浓度分别为0、0.001 mg/L、0.010 mg/L、0.060 mg/L、0.120 mg/L、0.200 mg/L。则工作曲线中亚硝酸盐氮以N计的含量为0、0.001 μg、0.01 μg、0.06 μg、0.12 μg、0.2 μg。
1.3 标准和样品测定取水样1.00 mL于反应管中,加入试剂R1:0.10 mL摇匀,放置20 min后于540 nm波长测定。
2 数学模型的建立及测量不确定度的来源 2.1 数学模型水样中亚硝酸盐氮的计算公式如下:
| $ {\rho _{\left( {N{O_2}-N} \right)}} = \frac{m}{V} $ |
式中:ρ(NO2-N)-水样中亚硝酸盐氮的质量浓度,
| $ {\rm{mg/L;}} $ |
m-相应吸光度下亚硝酸盐氮的含量,μg;
V-水样体积,mL。
因此,水样中亚硝酸盐氮浓度的相对不确定度是由m、V的相对不确定度以及微量自动分析仪和配套试剂盒的相对不确定度合成而来。
2.2 测量不确定度的来源根据分析方法的数学模型并对测量过程进行分析可以得出,饮用水中亚硝酸盐氮测量不确定度urel (ρ)主要来源于由标准曲线所得的亚硝酸盐氮含量产生的相对标准不确定度urel (m)以及由样品取样产生的相对不确定度urel (v)两个方面[4],此外还有微量自动分析仪和试剂盒产生的相对不确定度urel (仪)。其中urel (m)主要包括:
①样品重复性带来的不确定度;②标准曲线变动性带来的不确定度,采用最小二乘法拟合标准曲线求得样品硝酸盐氮质量浓度过程中引入的不确定度;③标准溶液配制中带来的不确定度,包括标准物质引入的不确定度、标准溶液配制过程中量器校准和移取定容、以及温度影响产生的不确定度。
测量不确定度来源及其影响因素如图 1所示。
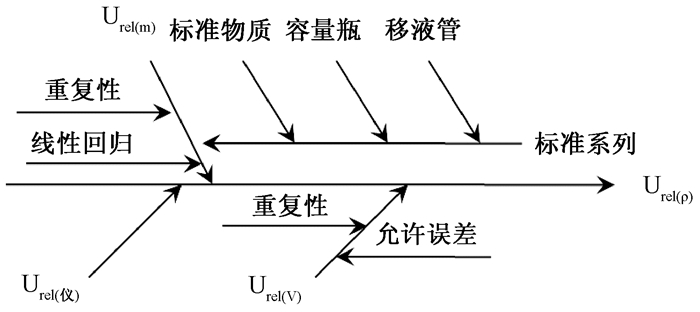
|
| 图 1 测量不确定度来源及影响因素图 |
3 不确定度分量的评定 3.1 根据标准曲线计算的亚硝酸盐氮含量产生的相对标准不确定度urel (m)[5] 3.1.1 线性回归产生的相对不确定度urel (回归)
标准曲线取5个点,每个点重复测定3次,结果见表 1。
| 序号 | m/μg | 吸光度/A | 平均值/ A | ||
| 1 | 0.001 | 0.009 | 0.010 | 0.009 | 0.009 |
| 2 | 0.01 | 0.036 | 0.035 | 0.035 | 0.035 |
| 3 | 0.06 | 0.186 | 0.184 | 0.185 | 0.186 |
| 4 | 0.12 | 0.364 | 0.364 | 0.364 | 0.364 |
| 5 | 0.2 | 0.607 | 0.607 | 0.608 | 0.607 |
拟合结果为A=3.0065m+0.0049,r=0.9999。水样平行测定6次(表 2)。
| 吸光度A | 0.222 | 0.221 | 0.221 | 0.219 | 0.220 | 0.221 |
| m/μg | 0.072 | 0.072 | 0.072 | 0.071 | 0.072 | 0.072 |
| m0/μg | 0.072 | |||||
由最小二乘法拟合标准不确定度为:
| $ {u_{\left( {回归} \right)}} = \frac{{{s_R}}}{b}\sqrt {\frac{1}{P} + \frac{1}{n} + \frac{{{{\left( {{m_0} - \bar m} \right)}^2}}}{{\sum\limits_{i = 1}^n {{{\left( {{m_i} - \bar m} \right)}^2}} }}} $ |
| $ 其中\;{s_R} = \sqrt {\frac{{\sum\limits_{i = 1}^n {{{\left( {{A_i} - \left( {b{m_i} + a} \right)} \right)}^2}} }}{{n - 2}}} $ |
| $ \bar m = \frac{{\sum\limits_{i = 1}^n {{m_i}} }}{n} $ |
式中:sR-标准曲线变动性的标准差;
m-标准曲线各校准含量的平均值,m -=0.078;
m0-样品溶液中硝酸盐氮含量,m0=0.072;
n-标准曲线的校准溶液测量次数,n=15;
P-被测样品溶液的测量次数,P=6;
a-标准曲线方程截距,a=0.0049;
b-标准曲线方程斜率,b=3.0065。
由上式可得sR=0.0013;u(回归)=0.0002;则
水样重复测定6次结果见表 2。单次测量的实验标准偏差:
| $ s\left( m \right) = \sqrt {\frac{{\sum\limits_{i = 1}^P {{{\left( {{m_i} - {m_0}} \right)}^2}} }}{{P - 1}}} = 0.0004 $ |
在日常分析中,测定两份样品报告平均值,故两次测定质量平均值的相对标准偏差为:
| $ {u_{rel\left( {重复} \right)}} = \frac{{s\left( m \right)}}{{{m_0}\sqrt 2 }} = \frac{{0.0004}}{{0.072 \times 1.414}} = 0.004 $ |
urel (标准系列)主要来源于:①标准物质的不确定度urel (标准物质);②标准系列配置过程中使用的0.1 mL刻度吸管、1 mL刻度吸管、10 mL刻度吸管、25 mL刻度吸管和100 mL容量瓶引起的不确定度。
3.1.3.1 标准物质亚硝酸盐氮标准物质GBW (E)080223,由国家标准物质中心提供,相对扩展不确定度2%。标准溶液产生的相对不确定度按正态分布,P=95%,取k=2。
| $ 因此\;{u_{{\rm{rel}}\left( {标准物质} \right)}} = \frac{{{u_{\left( {标准物质} \right)}}}}{c} = \frac{{2\% /2}}{{100}} = 0.0001mg/L $ |
溶液体积的不确定度由稀释重复性和体积误差构成。
稀释重复性:从实验得100 mL容量瓶稀释的重复性标准不确定度为u(V1)1=0.03mL。体积误差:100 mLA级容量瓶的允许误差为±0.10 mL[6],假设按三角形分布,u(V1)2=0.10/
| $ \begin{array}{l} {u_{rel}}\left( {{V_1}} \right) = \frac{{2 * u\left( {V1} \right)}}{{100}} = \frac{{2 * \sqrt {u\left( {{V_1}} \right){1^2} + u\left( {{V_1}} \right){2^2} + u\left( {{V_1}} \right){3^2}} }}{{100}} = \\ \frac{{2 * \sqrt {{{0.03}^2} + {{0.04}^2} + {{0.036}^2}} }}{{100}} = 0.0012{\rm{mL}} \end{array} $ |
从实验得0.1 mL刻度吸管的重复性标准不确定度为u(V2)1=0.001 mL。0.1 mL A级刻度吸管的允许误差为±0.002 mL[6],假设按三角形分布,u(V2)2=0.002/
因此,
| $ \begin{array}{l} {u_{rel(}}{V_2}) = \frac{{u\left( {{V_2}} \right)}}{{0.1}} = \frac{{\sqrt {u{{\left( {{V_2}} \right)}_1}^2 + u{{\left( {{V_2}} \right)}_2}^2 + u{{\left( {{V_2}} \right)}_3}^2} }}{{0.1}} = \\ \frac{{\sqrt {{{0.001}^2} + {{0.0008}^2} + {{0.00004}^2}} }}{{0.1}} = 0.014{\rm{mL}} \end{array} $ |
从实验得1 mL刻度吸管的重复性标准不确定度为u (V3)1=0.003 mL。1 mL A级刻度吸管的允许误差为±0.008 mL[6],假设按三角形分布,u (V3)2=0.008/
因此,
| $ \begin{array}{l} {u_{rel}}({V_3}) = \frac{{u\left( {{V_3}} \right)}}{1} = \frac{{\sqrt {u\left( {{V_3}} \right){1^2} + u\left( {{V_3}} \right){2^2} + u{{\left( {{V_3}} \right)}_3}^2} }}{1} = \\ \frac{{\sqrt {{{0.003}^2} + {{0.003}^2} + {{0.00036}^2}} }}{1} = 0.004{\rm{mL}} \end{array} $ |
从实验得10 mL刻度吸管的重复性标准不确定度为u (V4)1=0.012 mL。10 mL A级刻度吸管的允许误差为±0.05 mL[6],假设按三角形分布,u (V3)2=0.05/
因此,
| $ \begin{array}{l} {u_{rel}}({V_4}) = \frac{{u\left( {{V_4}} \right)}}{{10}} = \frac{{\sqrt {u{{\left( {{V_4}} \right)}_1}^2 + u{{\left( {{V_4}} \right)}_2}^2 + u{{\left( {{V_4}} \right)}_3}^2} }}{{10}} = \\ \frac{{\sqrt {{{0.012}^2} + {{0.020}^2} + {{0.0036}^2}} }}{{10}} = 0.002{\rm{mL}} \end{array} $ |
从实验得25 mL刻度吸管的重复性标准不确定度为u (V5)1=0.026 mL。20 mL A级刻度吸管的允许误差为±0.1 mL[6],假设按三角形分布,u(V5)2=0.1/
因此,
| $ \begin{array}{l} {u_{rel}}({V_5}) = \frac{{u\left( {{V_5}} \right)}}{{25}} = \frac{{\sqrt {u\left( {{V_5}} \right){1^2} + u{{\left( {{V_5}} \right)}_2}^2 + u{{\left( {{V_5}} \right)}_3}^2} }}{{25}} = \\ \frac{{\sqrt {{{0.026}^2} + {{0.041}^2} + {{0.009}^2}} }}{{25}} = 0.002{\rm{mL}} \end{array} $ |
由上述各分量得出:
| $ \begin{array}{l} {u_{rel\left( {标准系列} \right)}} = \\ \sqrt {{u_{rel\left( {标准系列} \right)}}^2 + {u_{rel(}}{V_{1)}}^2 + {u_{rel(}}{V_{2)}}^2 + {u_{rel(}}{V_{3)}}^2 + {u_{rel(}}{V_{4)}}^2 + {u_{rel(}}{V_{5)}}^2} \\ = \sqrt {{{0.0001}^2} + {{0.0006}^2} + {{0.014}^2} + {{0.004}^2} + {{0.002}^2} + {{0.002}^2}} \\ = 0.015 \end{array} $ |
| $ \begin{array}{l} {u_{rel\left( m \right)}} = \sqrt {{u_{rel\left( {_{回归}} \right)}}^2 + {u_{rel\left( {重复} \right)}}^2 + {u_{rel\left( {_{标准系列}} \right)}}^2} \\ \;\;\;\;\;\; = \sqrt {{{0.003}^2} + {{0.004}^2} + {{0.015}^2}} = 0.016 \end{array} $ |
取样体积用到1 mL A级刻度吸管,其相对不确定度urel (v)=0.004 mL。
3.3 微量自动分析仪和配套试剂盒产生的相对不确定度urel (仪)为了验证微量自动分析仪和配套试剂盒的稳定性,以确定仪器和试剂盒的不确定度,分别使用6个试剂盒对同一标准系列及水样进行测定,对比检测结果,计算其不确定度,结果见表 3。
| 试剂盒序号 | 标准曲线 | R | 样品 吸光度A |
样品含量 m/μg |
| 1 | A=3.016m | 0.9999 | 0.217 | 0.072 |
| 2 | A=3.166m+0.001 | 0.9999 | 0.232 | 0.073 |
| 3 | A=3.0065m+0.0049 | 0.9999 | 0.221 | 0.072 |
| 4 | A=3.023m+0.012 | 0.9999 | 0.230 | 0.072 |
| 5 | A=3.073m+0.008 | 0.9999 | 0.229 | 0.072 |
| 6 | A=2.999m+0.0014 | 0.9999 | 0.214 | 0.071 |
| 样品含量 平均值m0/μg |
0.072 | |||
标准差:
标准不确定度:
相对标准不确定度:
不同影响因素下所得不确定度数值见表 4。通过计算可得出合成ρ(NO2-N)的相对标准不确定度。
| 不确定度影响因素 | 数值 |
| 线性回归产生的相对不确定度urel (回归) | 0.003 |
| 重复测定计算的不确定度urel (重复) | 0.004 |
| 标准系列配制中带来的不确定度urel (标准系列) | 0.015 |
| 由样品取样产生的相对不确定度urel (v) | 0.004 |
| 由微量自动分析仪和试剂盒产生的相对不确定度urel (仪) | 0.003 |
| $ \begin{array}{l} {\rho _{\left( {{\rm{NO2 - N}}} \right)}} = \frac{m}{V} = \frac{{{m_0}}}{V} = \frac{{0.072}}{1} = 0.072{\rm{mg/L}}\\ {\rm{u}}\left( \rho \right) = {\rho _{\left( {{\rm{NO2}} - {\rm{N}}} \right)}} \times \sqrt {{u_{rel\left( m \right)}}^2 + {u_{rel\left( V \right)}}^2 + {u_{rel\left( {仪} \right)}}^2} \\ = 0.072 \times \sqrt {{{0.016}^2} + {{0.004}^2} + {{0.003}^2}} = 0.00{\rm{1mg/L}} \end{array} $ |
取包含因子k=2,置信区间P=95%,则扩展不确定度为:
| $ {\rm{U = k}} \times {\rm{u}}\left( \rho \right) = 2 \times 0.001 = 0.002{\rm{mg/L}} $ |
采用微量分光光度法测定饮用水中亚硝酸盐氮的含量,当k=2(95%置信概率),测量结果为(0.072±0.002) mg/L。
4 结论由表 4可以看出,微量分光光度法测定饮用水中亚硝酸盐氮的不确定度主要来源于标准系列的配制过程。因此实验中要注意合理选择标准物质,准确配制标准溶液,做好标准曲线。同时要控制适宜的环境温度,维护好仪器,从而减少测量不确定度。本研究在建立数学模型的时候,未能将诸如操作不规范、试剂混合不均匀等这些难以量化的影响因素纳入其中,因此有待进一步探讨与研究。
测量不确定度是对测量结果质量和水平的科学表达,可以校准方法的合理性,分析影响测量结果的主要成分。在检验工作中对方法的不确定度进行研究,有助于了解被测物质的真值所处的范围。尤其当检测值处于标准临界值时,对不确定度进行分析更有实际意义。本次试验测量结果为(0.072±0.002) mg/L (当k=2)。合成不确定度较小,证明该仪器运行稳定,处于较好的可控状态,检测结果有效,操作简便,维护简单,准确度好,适用于饮用水中亚硝酸盐氮的测定。
| [1] | 中华人民共和国卫生部, 中国国家标准化管理委员会. GB 5749-2006生活饮用水卫生标准[S].北京:中国标准出版社, 2007. |
| [2] | 中华人民共和国卫生部, 中国国家标准化委员会.GB/T 5750-2006生活饮用水标准检验方法[S].北京:中国标准出版社, 2007. |
| [3] | 韩嘉艺, 张振伟, 李晓明, 等. 微量分光光度法测定饮用水中的亚硝酸盐氮[J]. 中国卫生检验杂志, 2015, 25 (19): 3248–3249. |
| [4] | 钟小伶, 黄闽燕. 麝香草酚分光光度法测定水中硝酸盐氮的不确定度评定[J]. 中国卫生检验杂志, 2007, 17 (5): 914–915. |
| [5] | 中国金属学会分析测试分会. CSM 01 01 01 02-2006分光光度法测量结果不确定度评定规范[S].北京:中国标准出版社, 2006. |
| [6] | 国家质量监督检验检疫总局. JJG 196-2006常用玻璃量器检定规程[S].北京:中国计量出版社, 2007. |



