2. 中国地质科学院岩溶地质研究所, 桂林 541004
2. Institute of Karst Geology, Chinese Academy of Geological Sciences, Guilin 541004
国内地下水污染的严峻形势自20世纪80年代开始已持续了近40年, 华北平原及长三角地区工业的迅速发展造成了过度的地下水抽采和严重的水质污染, 威胁着人们的生活环境(薛禹群等, 2007;王大纯等, 2005).其中, 地下水中有机污染物的治理和修复问题受到了越来越多的关注(郭高轩, 2011;钟佐燊, 2001), 生物降解修复作为修复方法之一也得到了广泛的研究和应用(李家伦等, 1999;Zheng et al., 2009;阳艾利, 2013).例如, Rifai等(1997)将莫诺动力学方程(Monod, 1949)应用到有机物作为基质的微生物降解过程中, 提出了常见烃类污染物包括苯、甲苯、乙苯与二甲苯(BTEX)的快速生物降解反应模型;Alexander(1994)认为在高浓度情况下, 许多有机污染物对将其作为营养源的微生物是有毒性的, 微生物群体的生长率可能被抑制, 因此, 发展了受高浓度抑制生长的莫诺动力学方程;Essaid等(1997)进一步提出多组分莫诺动力学反应理论, 认为某一组分的生物降解反应受到各种物质浓度的限制.
值得一提的是, 上述早期建立的生物降解模型往往未考虑完整的水化学反应体系, 例如, 降解过程可能会导致pH的变化, 而pH反过来又会影响微生物的生长.随着监测微生物自然降解作用被作为地下水污染治理策略, 多组分反应迁移也受到越来越多的重视(NRC, 2000).Lu等(1999)基于多组分反应运移软件RT3D模拟了BTEX多组分的野外场址的生物自然降解过程; 后续大量的相关研究(Prommer et al., 2009;Pooley et al., 2009)都说明了生物降解反应运移的数值模拟研究对污染修复的指导意义.
与以往的地下水流和溶质运移问题不同, 地下水生物降解反应运移问题是水流系统、溶质运移和化学反应系统的综合, 包含了多个水文地质参数和水文地球化学参数, 同时多组分模拟系统使得模拟结果包含多种不同类型的观测数据, 这些都给地下水反应运移模型的参数估计带来了困难.目前地下水反应运移模型通常采用非线性回归法和贝叶斯方法进行参数估计, 代表性的研究如Bachmaf等(2011)利用非线性参数估计软件PEST(Doherty et al., 2004)对水文地球化学反应的相关参数进行了估计;Carniato等(2014)利用贝叶斯方法对反应运移模型进行参数估计, 并分析讨论了残差相关性及模型误差的问题.由于地下水反应运移模型参数众多, 故也开展了不少模型不确定性分析和参数估计相关性的研究, 例如, Nitzsche等(2000)在六价铀的吸附柱实验中通过Monte Carlo模拟进行了化学反应数据库的不确定性研究;Tebes-Stevens等(2001)比较了反应运移模拟中运移参数和反应参数对结果影响的不确定性大小, 通过比较一个二维区域地下含水层中六价铀水相络合反应中参数的局部敏感性系数, 得出了运移参数和反应参数对模拟结果影响同等重要的结论;林青等(2011)在运移数值模拟的研究中采用基于贝叶斯理论的GLUE方法对土壤重金属溶质运移中的吸附特征参数等进行了不确定性分析, 吸附特征参数的高敏感度表明了水文地球化学反应是影响溶质运移的重要因素.
本文基于反应运移数值软件PHT3D v2.1(Prommer et al., 2010), 构建了一个污染场地地下水中有机污染生物降解的理想正问题.针对以往模型参数反演过程中多数研究者(杨建锋等, 2000;Steefel et al., 2003;崔凯等, 2004;Zhang et al., 2008)忽略观测数据权重的影响(对权重不予考虑或全部置为1)的问题, 在参数估计过程中对比使用不同的权重进行参数估计的结果, 以探讨观测数据权重对于参数估计的影响.
2 生物降解反应模型算例(A synthetic case of biodegradation model)以文献(Prommer et al., 2009)中的地下水生物降解模型为基础, 选择沿污染羽中轴线的一个断面为研究对象, 模拟无氧环境中硫酸盐还原条件下多种有机污染物的降解过程.污染场地的模型概念示意图如图 1所示, 模拟剖面长度40 m, 垂直方向2 m.假定地表被混凝土和建筑物覆盖, 降雨入渗可忽略;假定饱和含水层为均质砂层, 渗透系数为0.001 m·s-1, 潜水水力梯度为0.006.研究区内存在两个持续泄漏单环芳烃(BTEX)和多环芳烃(PAH)的NAPLs源区, 上部源区的厚度为0.3 m, 下部的源区由于泄漏量较小, 为残留NAPLs, 厚度仅有0.05 m.下游15 m处设一多级分层监测井, 自标高32.625~33.825 m, 每隔0.05 m取样(共25个取样点), 总模拟时间为60 d.
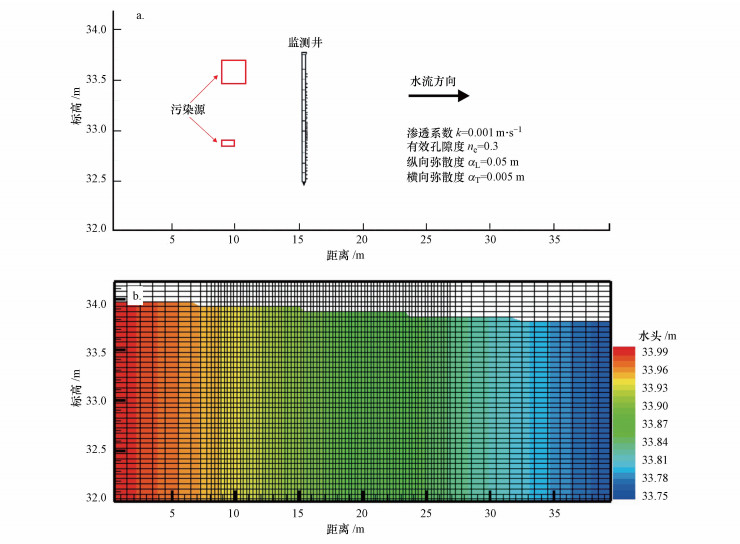 |
| 图 1 模型概念示意图(a)和网格离散示意图(b) Fig. 1 The schematic diagram of conceptual model (a) and grid discretization(b) |
假定各有机物的动态溶解速率为:
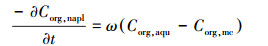
|
(1) |
式中, Corg, napl和Corg, aqu分别是有机物的不可流动相(NAPLs)和溶解相浓度(mol·L-1), Corg, mc为有机物的多相溶解度(mol·L-1), ω为速率迁移常数.根据拉乌尔定律(Raoult′s law), Corg, mc可以由已知的单相溶解度和在NAPLs混合物中的多组分摩尔分数γorg计算得出:
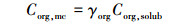
|
(2) |
式中, Corg, solub为有机物的单相溶解度(mol·L-1).由于ω和γorg难以室内直接测定, 故需要在模型校正时估计.该算例反应体系中假设LNAPLs有机物共8种:苯(Benzene, C6H6)、甲苯(Toluene, C7H8)、乙苯(Ethylbenzene, C8H10)、邻二甲苯(O-xylene, C8H10)、间/对二甲苯(m/p-xylene, C8H10)、萘(Naphthalene, C10H8)、苊(Acenaphthene, C12H10)及芴(Fluorine, C13H10).表 1给出了研究区平衡水相溶液的组分浓度.
| 表 1 初始及上游边界水组分浓度 Table 1 Initial and upstream boundary water concentration |
假设微生物活动以吸附于沉积物上的硫酸盐还原菌(SRB, Sulfate Reducing Bacteria)来表示, 其对芳香烃的生物降解反应起着关键作用(Anneser et al., 2008;Winderl et al., 2008;Wisotzky et al., 1997).假设SRB的浓度受到生长和衰退的影响:
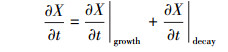
|
(3) |
式中, X是硫酸盐还原菌SRB的浓度(mol·L-1).微生物的生长量化为norg种不同芳香烃的有机碳转化成细胞物质的转化速率:
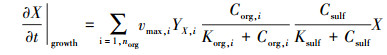
|
(4) |
式中, vmax为基质最大摄取速率(s-1), Corg是有机碳化合物的浓度(mol·L-1), Csulf是硫酸盐浓度(mol·L-1), Korg和Ksulf为相应的半饱和常数(mol·L-1), YX为表示微生物生长量的化学计量系数, 其中, vmax, i在室内难以测定, 故常被选作模型反演的参数.细菌的衰减可能受很多因素的影响, 如原生动物受到擦伤(Protozoan Grazing)、污染物的毒性及缺乏营养物质等.对细菌衰减项采用标准线性假设, 与微生物量的浓度成正比, 生物量衰减速率表示为:
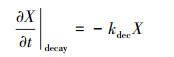
|
(5) |
式中, kdec为衰减速率常数(s-1).降解过程中第i种有机化合物的去除速率与微生物的生长速率成正比:
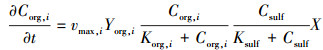
|
(6) |
降解过程中有机化合物的化学计量系数Yorg, i可以由平衡的降解反应来确定, 由于该平衡反应将生长合并在一起, 因此, 会将一部分降解的有机碳吸收合并为细胞质量.假设硫酸盐还原菌的生物效率为10%, 在硫酸盐还原条件下甲苯降解反应的化学方程式见式(7), 其余反应的化学方程式见表 2(假设10%的有机碳转化为生物量).
| 表 2 包括微生物生长在内的降解反应方程式 Table 2 Degradation reaction equations including microbial growth |
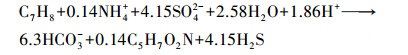
|
(7) |
由于有机污染物的主要组分为单环芳烃甲苯、乙苯、对二甲苯(PX)和多环芳烃萘, 故选择与上述组分密切相关且控制生物降解过程(同时室内也不宜确定)的12个参数进行参数估计.其中, 每个组分各3个参数, 包括NAPL溶解速率迁移常数ω、多组分摩尔分数γorg及生物降解基质最大摄取率vmax, i.
为了便于对比不同权重影响下的参数反演评价, 假设一组真实值(图 2)代入到正模型中, 以60 d后观测井中的计算值加上一组随机误差得到观测数据用于后续的参数估计, 假定观测误差服从标准正态分布, 均值为0, 标准差为真实值的5%.观测数据一共6组, 除了4种与反演参数直接相关的降解物质外, 还包括pH和硫酸盐两个观测组.每组25个观测值, 共150个观测数据.
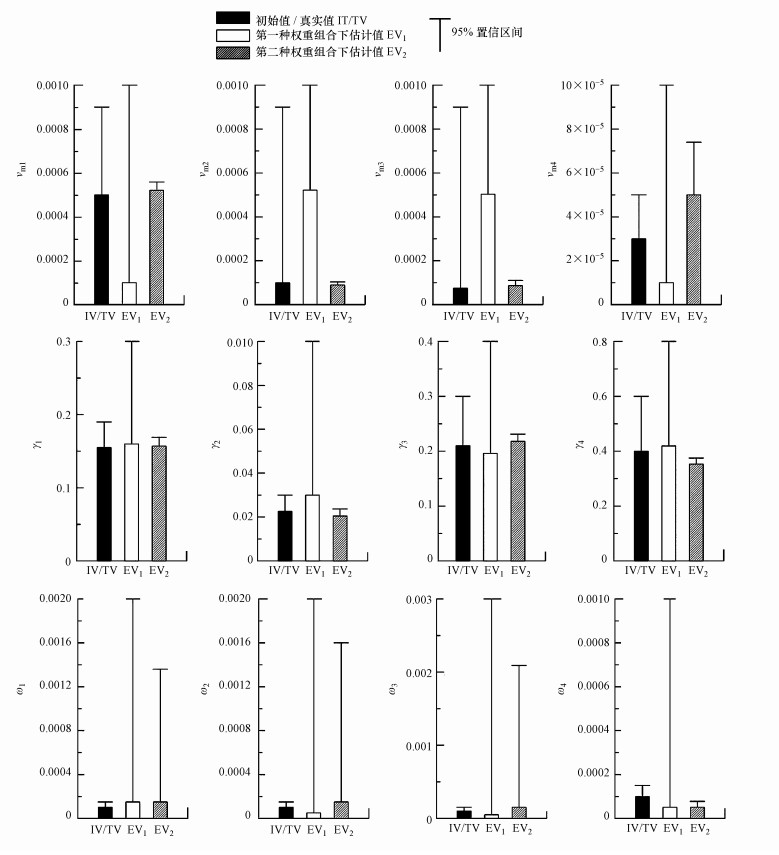 |
| 图 2 不同权重下参数估计值及95%置信区间与真实值及参数估计范围对比图(对于真实值,置信区间的图例表示参数估计的范围) Fig. 2 Estimated parameters and 95% confidence intervals for different observation weights |
定义参数估计的目标函数为:
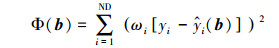
|
(8) |
式中, ωi为权重, b为包含NP个待估参数的向量, yi为观测值, ŷi为模拟值, ND为观测值个数.采用PEST软件(Doherty et al., 2004)进行参数估计, 获得参数估计值、95%置信区间及相关系数矩阵.
3.1 不同权重组合对参数估计的影响在以往参数估计过程中, 估计者通常不关心观测数据的权重, 而采用默认值1代替.因此, 本文拟对比不同权重组合下的参数估计结果, 从而探讨观测数据权重对模型参数估计的影响.第一种权重组合是采用传统做法将权重默认为1;第二种权重组合则是由观测误差的标准差计算观测值权重(也即权重等于观测误差标准差的倒数, 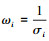
图 2为两种权重组合的参数估计结果及其95%置信区间, 图 3为两种不同权重组合下参数估计后各组分浓度模拟曲线与观测结果比较图.由图 2可以看出, 第一种权重组合下参数估计值与真实值相差较大, 置信区间也较大, 而第二种权重组合下参数估计值与真实值更接近且置信区间也小于前者.由图 3可以看出, 第一种权重组合下模拟值与观测值偏离较大, 而第二种权重组合的拟合程度明显更好.以上对比得出:第二种权重组合即考虑观测数据权重的参数估计结果与真实值更为接近, 不确定性小于第一种权重组合, 参数拟合程度也更好.
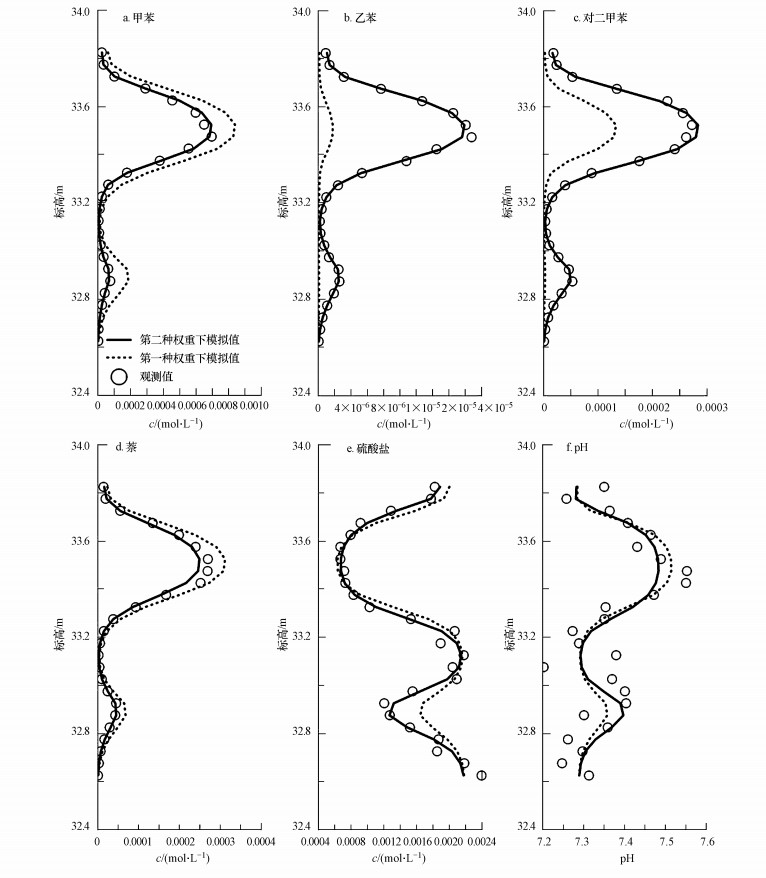 |
| 图 3 不同权重组合反演参数下的各组分浓度模拟曲线与观测结果比较图 Fig. 3 Comparison of simulation curves and observations of different weights for each component of the model under different weights |
表 3为不同权重组合下各观测组对目标函数的贡献值, 其中, 第一种权重组合反演结果中各观测组对目标函数的贡献值相差很大, 主要受控于pH观测组, 而第二种权重组合下各观测组对目标函数的贡献大致相同.由于pH观测值的数量级与其他参数相差很大, 因此, 第一种权重组合下模型拟合过程中会出现偏向于拟合数量级大的pH观测数据(图 3f)而其他数量级小的观测数据拟合较差(图 3b)的情况, 这正说明了参数估计过程中需考虑观测数据的权重.
| 表 3 各观测组对目标函数的贡献值 Table 3 The contribution of the objective function of the observation group |
进一步绘制两种不同权重组合下观测数据和模拟值之间的散点图(图 4)来说明参数估计的整体拟合效果.由图 4可以看出, 两种权重组合下, pH观测组的散点均大致分布在45°线两侧;而其余观测组的观测数据由于数值较小, 两种权重组合条件下的散点在图中的分布差异显著, 其中, 第二种权重组合下散点较均匀地分布在45°线上, 拟合程度高, 而第一种权重组合下散点距离45°线偏差较大.这也说明了当反应运移模型的不同观测组数据数量级相差较大时, 若不考虑观测数据的权重, 则会出现偏向于拟合观测数据的高值, 而导致观测数据的低值拟合较差的情况.因此, 对于多组分反应运移模型参数估计应充分考虑观测数据的权重, 从而真实地反映不同类型观测数据的观测误差及其对目标函数的贡献值, 通过权重准确反映观测精度并起到去量纲化的作用.
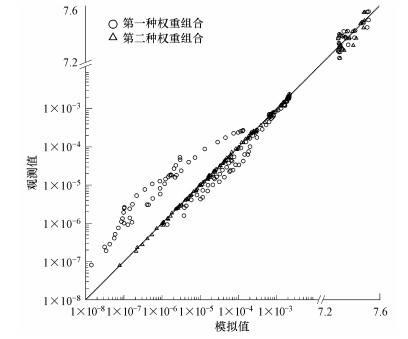 |
| 图 4 所有观测组观测值与模拟值的散点图 Fig. 4 The scatter plot between all observations (vertical axis) and simulations (horizontal) |
从图 2可以看出, 在考虑了观测数据权重的情况下, 模拟值与真实值之间仍然存在一定的偏差.由于地下水反应运移问题为水流系统、溶质运移和化学反应系统的综合, 包含了多种类型的多个参数, 因此, 对参数的敏感性研究就变得十分重要(郑菲等, 2014).
定义局部敏感度为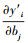
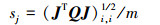
|
(9) |
式中, m为非零权重观测值的个数, Q为权重矩阵, 通过加权将局部敏感度受参数量纲的影响标准化;J为雅可比偏导数矩阵, 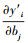
对模型进行局部敏感度分析, 如果有M个参数要进行敏感性分析, 除了运行一次基本数值模拟外, 还要附加运行数值模型M次, 每次让待求参数有一个微小变化Δαk, 其余参数保持不变, 这样依次改变每一个参数.正如Zheng等(2002)指出的, 参数变动Δαk太小会造成模型的差别因变量计算值的差别微不足道或者四舍五入的误差而显得黯然失色.反过来, Δαk太大的变动也会使敏感度不精确.因此, 根据经验, Δαk取值一般为1%~5%为好.图 5为第二种权重组合最优参数估计值条件下Δαk为2%的局部敏感度结果, 可见不同参数对于不同观测组(所有观测组与分别的6个观测组)的敏感度有明显差异.总体看来, 模型中生物降解反应参数最敏感, 其次是萘组分的溶解速率迁移常数, 多相溶解度摩尔分数γ的敏感度较小.为了降低参数估计的难度, 后续可考虑固定多相溶解度摩尔分数的4个参数.
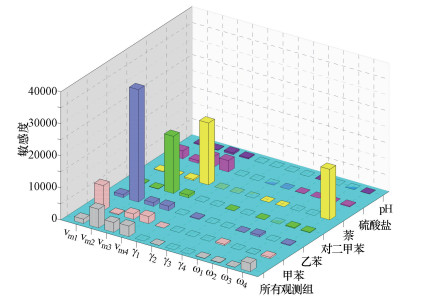 |
| 图 5 反演参数相对于不同观测组的敏感度 Fig. 5 Composite parameter sensitivities for different observation groups |
本文基于PHT3D构建了一个理想的生物降解反应运移模拟正问题, 以此对比讨论了不同权重组合对反应运移模型参数估计的影响, 得出以下结论:
1) 由于反应运移模型中包含多个不同组分, 不同类型的观测数据数量级相差较大, 若不考虑观测数据的权重(即默认观测数据的权重为1), 则会出现偏向于拟合观测数据的高值, 而导致观测数据的低值拟合较差的情况.因此, 对于多组分反应运移模型参数估计应充分考虑观测数据的权重, 从而真实地反映不同类型观测数据的观测误差及其对目标函数的贡献值, 此外通过权重还可以准确反映观测精度并起到去量纲化的作用, 从而更准确地估计模型参数.对于本例生物降解模型, 参数估值的准确与否将显著影响污染场址生物修复效率的评估.
2) 参数的敏感性结果显示, 参数对于不同观测组数据的敏感度有明显差异.对于本例生物降解模型, 降解反应参数最敏感, 其次是溶解速率迁移常数, 多相溶解度摩尔分数敏感度较小.基于敏感性分析设计和优化观测数据的采集将有利于反应运移模型的参数估计, 由于反应运移模型参数众多, 通过敏感性分析可将部分敏感度较低的参数在参数估计前固定, 从而降低参数维数, 在一定程度上降低参数估计的难度.
| [${referVo.labelOrder}] | Alexander M. 1994. Biodegradation and Bioremediation[M]. San Diego: Academic Press: 73 -97. |
| [${referVo.labelOrder}] | Anneser B.2008.Spatial and temporal dynamics of biogeochemical gradients in a tar oil-contaminated porous aquifer-biodegradation processes revealed by high-resolution measurements[D].Trostberg:Universität Tübingen.15-26; 55-73 http://cn.bing.com/academic/profile?id=1572021445&encoded=0&v=paper_preview&mkt=zh-cn |
| [${referVo.labelOrder}] | Bachmaf S, Merkel B J. 2011. Estimating water chemistry parameters from experimental data using PEST with PHREEQC[J]. FOG-Freiberg Online Geoscience , 28 : 1–18. |
| [${referVo.labelOrder}] | Carniato L, Schoups G, van de Giesen N. 2014. Inference of reactive transport model parameters using a Bayesian multivariate approach[J]. Water Resources Research , 50 (8) : 6406–6427. DOI:10.1002/wrcr.v50.8 |
| [${referVo.labelOrder}] | 崔凯, 李宝元, 李兴斯, 等.2004. 非饱和土中镉离子传输模型参数反演[J]. 水科学进展 , 2004, 15 (6) : 700–705. |
| [${referVo.labelOrder}] | Doherty J. 2004. PEST-Model-Independent Parameter Estimation, User's Manual(5th edition)[M]. Brisbane Australia: Watermark Numerical Computing: 501 -523. |
| [${referVo.labelOrder}] | Essaid H I, Bekins B A. 1997. BIOMOC, A Multispecies Solute-Transport Model with Biodegradation[M]. Menlo: US Geological Survey: 14 -25. |
| [${referVo.labelOrder}] | 郭高轩.2011. 地下水有机物污染修复标准探讨[J]. 水资源保护 , 2011, 27 (2) : 37–41. |
| [${referVo.labelOrder}] | Hill M C, Tiedeman C R. 2006. Effective Groundwater Model Calibration:With Analysis of Data, Sensitivities, Predictions, and Uncertainty[M]. New York: Wiley-Interscience: 47 . |
| [${referVo.labelOrder}] | 李家伦, 孙菽芬, 洪钟祥.1999. 孔隙裂隙含水层生物降解的模型参数试验[J]. 环境科学学报 , 1999, 19 (6) : 591–596. |
| [${referVo.labelOrder}] | Lu G, Clement T P, Zheng C, et al. 1999. Natural attenuation of BTEX compounds:Model development and field-scale application[J]. Groundwater , 37 (5) : 707–717. DOI:10.1111/gwat.1999.37.issue-5 |
| [${referVo.labelOrder}] | 林青, 徐绍辉.2011. 饱和多孔介质中重金属运移参数的敏感度分析[J]. 环境科学学报 , 2011, 31 (1) : 136–143. |
| [${referVo.labelOrder}] | Monod J. 1949. The growth of bacterial cultures[J]. Annu Rew Micorbiol (3) : 371–394. |
| [${referVo.labelOrder}] | Nitzsche O, Meinrath G, Merkel B. 2000. Database uncertainty as a limiting factor in reactive transport prognosis[J]. Journal of Contaminant Hydrology , 44 (3/4) : 223–237. |
| [${referVo.labelOrder}] | N RC. 2000. Natural Attenuation for Groundwater Remediation. Washington DC:National Academies Press[M]. : 106 -114. |
| [${referVo.labelOrder}] | Pooley K E, Blessing M, Schmidt T C, et al. 2009. Aerobic biodegradation of chlorinated ethenes in a fractured bedrock aquifer:quantitative assessment by compound-specific isotope analysis (CSIA) and reactive transport modelling[J]. Environmental Science & Technology , 43 (9) : 7458–7464. |
| [${referVo.labelOrder}] | Prommer H, Anneser B, Rolle M, et al. 2009. Biogeochemical and isotopic gradients in a BTEX/PAH contaminant plume:model-based interpretation of a high-resolution field data set[J]. Environmental Science & Technology , 43 (21) : 8206–8212. |
| [${referVo.labelOrder}] | Prommer H, Post V. 2010. PHT3D, a reactive multicomponent transport model for saturated porous media[J]. User's manual v2.10[J].Groundwater , 48 (5) : 627–632. |
| [${referVo.labelOrder}] | Rifai H, Newell C, Gonzales J, et al. 1997. BIOPLUMEⅢNatural Attenuation Decision Support System Version 1.0 User'S Manual[J]. Brooks AFB, San Antonio, Texas:Air Force Center for Environmental Excellence : 82–106. |
| [${referVo.labelOrder}] | Steefel C I, Carroll S, Zhao P, et al. 2003. Cesium migration in Hanford sediment:a multisite cation exchange model based on laboratory transport experiments[J]. J Contam Hydrol , 67 (1/4) : 219–246. |
| [${referVo.labelOrder}] | Tebes-Stevens C L, Espinoza F, Valocchi A J. 2001. Evaluating the sensitivity of a subsurface multicomponent reactive transport model with respect to transport and reaction parameters[J]. Journal of Contaminant Hydrology , 52 (1/4) : 3–27. |
| [${referVo.labelOrder}] | Wisotzky F, Eckert P. 1997. Sulfat-dominierter BTEX-Abbau im Grundwasser eines ehemaligen Gaswerksstandortes[J]. Grundwasser , 2 (1) : 11–20. DOI:10.1007/s767-1997-8508-z |
| [${referVo.labelOrder}] | 王大纯, 张人权, 梁杏. 2005. 水文地质学基础[M]. 北京: 地质出版社: 164 -174. |
| [${referVo.labelOrder}] | Winderl C, Anneser B, Griebler C, et al. 2008. Depth-resolved quantification of anaerobic toluene degraders and aquifer microbial community patterns in distinct redox zones of a tar oil contaminant plume[J]. Applied and Environmental Microbiology , 74 (3) : 792–801. DOI:10.1128/AEM.01951-07 |
| [${referVo.labelOrder}] | 薛禹群, 谢春红. 2007. 地下水数值模拟[M]. 北京: 科学出版社: 1 -5. |
| [${referVo.labelOrder}] | 阳艾利.2013.基于模拟的地下水石油污染风险评估与修复过程优化技术研究[D].北京:华北电力大学.15-31 http://cdmd.cnki.com.cn/Article/CDMD-10079-1013315761.htm |
| [${referVo.labelOrder}] | 杨建锋, 李宝庆, 马瑞, 等.2000. 地下水浅埋区土壤水分运动参数田间测定方法探讨[J]. 水文地质工程地质 , 2000, 27 (1) : 1–3. |
| [${referVo.labelOrder}] | 钟佐燊.2001. 地下水有机污染控制及就地恢复技术研究进展(二)[J]. 水文地质工程地质 , 2001, 28 (4) : 26–31. |
| [${referVo.labelOrder}] | Zhang F, Luo W, Parker J C, et al. 2008. Geochemical modeling of reactions and partitioning of trace metals and radionuclides during titration of contaminated acidic sediments[J]. Environ Sci Technol , 42 (21) : 8007–8013. DOI:10.1021/es800311m |
| [${referVo.labelOrder}] | Zheng C, Bennett G D. 2002. Applied Contaminant Transport Modeling(Second Edition)[M]. New York: Wiley-Interscience . |
| [${referVo.labelOrder}] | Zheng C, Bennett G D, 孙 晋玉, et al. 2009. 地下水污染物迁移模拟[M]. 第二版. 北京: 高等教育出版社: 224 -227. |
| [${referVo.labelOrder}] | 郑菲, 施小清, 吴吉春, 等.2014. 深部咸水层CO2地质封存数值模拟参数的全局敏感性分析:以苏北盆地盐城组为例[J]. 吉林大学学报(地球科学版) , 2014, 44 (1) : 310–318. |
 2016, Vol. 36
2016, Vol. 36


