水资源优化配置是结合系统分析理论和优化技术,综合分析水资源开发利用对社会经济、生态环境的影响,将有限的水资源在各子区、各用水部门之间进行优化调配,以获得最佳的综合效益(刘昌明等,1996).其内涵主要包括两个方面:①从分配效率上提高水资源配置,合理调节各行业、各部门之间的用水,缓解竞争用水压力;②从利用效率上提高水资源分配,注重水资源的循环利用(李婷贤,2013).
国内对于水资源优化配置的研究始于20世纪60年代,从始至今,不论是模型还是算法,都取得了丰硕的成果(戴国瑞等,1983).研究规模从开始的水库优化配置发展到多区域、多水源和多用户优化调度研究;研究内容从单一的水资源经济效益向水资源可持续发展转变;研究模型逐渐从小规模、单目标发展到大规模、多目标、多层次的水资源配置;研究方法从单一数学规划方法向多种数学规划方法与模拟技术组合模型发展.规划设计是水资源配置的一种有效管理手段(Lu et al., 2009;Li et al., 2014;于森等,2015).在规划设计过程中,需要考虑供需水量、经济参数、水体污染物排放等不确定因素,这些因素使水资源管理系统规划变得更加复杂.围绕水资源管理系统中的不确定信息,诸多学者开展了一系列研究,主要的方法包括区间线性规划和随机规划.例如,张静等(2009)基于区间两阶段随机规划方法,构建了多水源联合调度优化模型,该模型充分考虑了系统中的不确定信息,区间结果可以为决策者提供灵活的调控方案.莫淑红等(2014)提出区间多阶段随机规划模型,并应用于陕西省宝鸡市冯家山水库,模型的优化结果能够权衡系统经济效益、系统风险和经济惩罚.这两种模型采用区间参数和随机参数反映系统的不确定信息,但是其仅考虑单一的规划目标,而通常的水资源配置是涉及社会、经济和环境的多目标决策问题.多目标模型虽然可以得到综合情况下的最优方案,但忽略了水资源管理者和使用者之间相互制约、相互矛盾的层次关系.而双层规划模型作为多目标模型的一种特殊形式,其可以反映系统的多目标、多层次和多决策者的特征(Hathhorn et al., 1989;He et al., 2011).吴丹等(2012)以大凌河流域初始取水权和排污权为研究对象,结合双层规划理论,建立流域二维水权配置模型,模型结果实现了社会经济目标和生态环境目标的集成化,水资源数量和质量的统一.基于流域水权分配概念,Xu等(2013)运用双层规划方法处理水资源分配问题,模型分别以社会效益和经济效益为上层和下层目标函数.但这些双层规划模型并没有考虑水资源管理系统中的水价因素和不确定因素.
水资源的配置是由管理者和使用者共同完成的.鉴于我国水市场并非完全市场化的情况,区域水资源配置实质上可分为两个层次,其中,调控水价的管理者作为第一层次,各用水部门的配置作为第二层次,管理者通过水价的市场调节作用来影响用水者对水资源的利用,部门的取水量又反作用于水资源利用的经济效益和环境影响而引起水价的调整.因此,本研究以北京市丰台区水资源管理系统为例,在供需水量预测分析的基础上,将区间双层规划模型用于水资源系统管理(Interval Bi-level Programming Model for Water Resources Management,IBPM-WRM),其中,以区间参数表征系统的不确定性信息,通过交互式算法和模糊满意度算法获得合理的水资源配置方案,以解决水资源系统经济效益、配水量和环境影响问题,最终实现区域水资源管理系统的可持续发展.
2 水资源管理系统双层规划设计结构(Bi-level programming design framework of water resources management system)本文采用双层规划方法对区域水资源管理系统进行优化.上层为经济效益模块,以净水价格为决策变量;下层为调度优化模块,以分配水量为决策变量,用于实现各部门最优的配水方案.在双层决策过程中,上层优化结果会影响下层目标和约束条件,而下层优化结果也需要反馈给上层决策者,从而实现上层和下层的最优决策.追求经济效益最大化是水资源管理的普遍目标,因此,其级别优于配水量最小化的实现.同时,为使优化结果更加切合实际案例的要求,本文采用指标分析法对研究地区的需水量开展研究.图 1展示了双层规划的逻辑结构.
 |
| 图 1 双层规划逻辑图 Fig. 1 Logic diagram of the bi-level programming |
双层规划方法于1973年由Bercken和Mcgill首次提出.双层规划在水资源管理、地下水修复、地表水水体污染控制等领域已有研究报道.数学上的双层规划模型可概述如下(Calvete et al., 2010;Zheng et al., 2011):
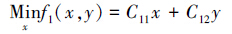
|
(1) |
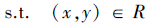
|
(2) |
y是如下问题的解:
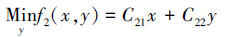
|
(3) |
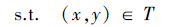
|
(4) |
式中,f1(x,y)和f2(x,y)分别代表上层和下层目标函数;x和y分别代表上层和下层决策变量;C11、C12、C21和C22分别是相应的常数向量;R和T分别表示上层和下层约束条件的限制空间.本文基于模糊满意度算法对双层规划问题进行求解,具体步骤如下(Shih et al., 1999;Kasperski,2005):
第一步:上层目标和下层目标分别进行独立求解,得到相应的解,即(xU,yU,f1U)和(xL,yL,f2L);通过比较上层和下层目标的求解结果,若(xU,yU)=(xL,yL),则可以得到最终的最优解.但上层目标和下层目标往往是互相矛盾的,所以上述假设难以成立.
第二步:给上层决策变量x设定一个容忍阈值,并建立如下的三角隶属度函数:
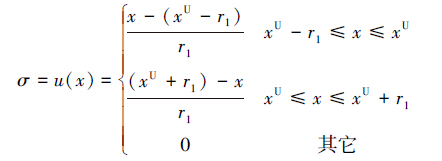
|
(5) |
式中,σ或u(x)代表上层决策变量x的满意度;(xU-r1)和(xU+r1)分别代表上层决策变量x的左侧和右侧容忍阈值.
第三步:上层目标函数设定一个容忍阈值,由于目标函数是求最小化问题,所以假定f1(x,y)<f1U是完全可以接受的,而f1(x,y)>f′1是完全不能接受的,其中,f′1代表上层目标函数最高的容忍值.最高容忍值的确定可以通过决策者的主观判定或分情景讨论,但这两种方式往往会忽略上层和下层决策目标的交互作用.基于此,本研究假定双层规划中的上层和下层目标相互对立,f′1可通过将下层目标的求解方案(xL,yL)代入上层目标函数计算得出,即f′1=f1(xL,yL),并建立如下的隶属度函数:

|
(6) |
式中,η或u′(f1(x,y))代表上层目标函数的满意度.
第四步:下层目标函数也需要设定一个容忍阈值,其隶属度函数如下式所示:

|
(7) |
式中,τ或u′′(f2(x,y))代表下层目标函数的满意度;f′2代表下层目标函数最高的容忍值,同理,f′2=f2(xU,yU).
第五步:为同时满足上层目标和下层目标的满意度,引入全局满意度λ,并建立关系式λ=Min{σ,η,τ},则上述双层规划问题就可以转化成求解最大的λ值,具体公式如下:
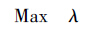
|
(8) |
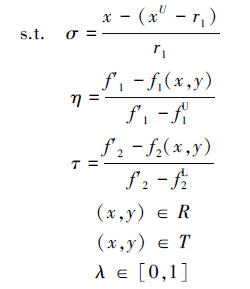
|
(9) |
双层规划很好地反映了系统的层次性结构,但缺少对系统的不确定性信息的描述.例如,在现实水资源管理系统中存在着多重不确定性因素,这可能导致在实际问题中不能确定其真实值,而区间能很好地诠释这些不确定因素,同时为决策者提供多种替代方案(刘三省等,2014).区间线性规划由Huang等于1992首次提出,可以根据Huang等提出的交互式算法求解模型(Huang et al,1992).以目标函数最小化问题为例,先构造相应于目标函数下界的子模型,然后在下界求解的基础上,再构造上界子模型,从而得到关于模型的不确定解.交互式算法和模糊满意度算法的共同点是模型在求解过程中与不同界域、不同层面的目标函数进行信息交流,这样获得的结果更符合决策者的需求.
在区间双层规划模型建立之前,提出以下几点假设:①模型中的供水效益系数主要是通过参考相关文献而确定,其值在不同规划期内保持不变;②模型中只考虑一种水体污染物(即化学需氧量,COD);③不同部门的污水排放系数和COD排放值均依据城市排水工程规划中的相关指标和案例城市具体情况,其值在不同规划期内也保持不变.另一方面,本研究中的模型主要是针对案例城市而开展的,若其被应用在其他城市,相应的目标函数、约束条件和模型参数均需要做出调整.
3.2 上层经济效益模块 3.2.1 目标函数上层以水资源管理系统的经济效益最大化为目标函数:
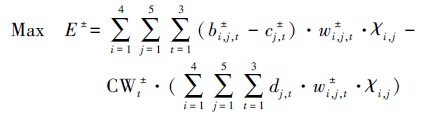
|
(10) |
式中,“±”代表区间值;i代表水源,i=1为地表水,2为地下水,3为再生水,4为客水;j代表用水部门,j=1为农业,2为工业,3为第三产业,4为城市生活,5为生态环境;t代表规划期,t=1为2016—2020年,t=2为2021—2025年,t=3为2026—2030年;E为规划期内水资源管理系统的经济效益(元);bi,j,t和cj,t分别为效益系数和净水价格(元·m-3);wi,j,t为t时期i水源分配给j用户的水量(m3);χi,j为i水源与j用户供水关系,χi,j=1表示存在供水关系,χi,j=0表示无供水关系;CWt为t时期的污水处理费用(元·m-3);dj,t为t时期j用户的废水排放系数.
3.2.2 约束条件上层约束条件主要包括净水价格约束和系统协调度约束.其中,净水价格约束:模型要求净水价格须限制在一定的范围内(式(11)).
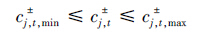
|
(11) |
水环境-经济协调发展约束(邓彩琼,2005):上层约束中引入“区域协调发展指数”这一概念,以表征区域水资源管理系统中经济、环境、社会的协调发展程度.由于水资源的经济效益与水价方案紧密相关,所以,这条约束实质上也是针对水价因素(式(12)).
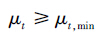
|
(12) |
式中,cj,t,min和cj,t,max分别为最低和最高净水价格(元·m-3);μt和μt,min分别为区域协调发展指数和协调发展最低指数,区域协调发展最低指数视实际情况而定,文中取0.8.水环境-经济协调发展约束的具体要求如下.
水资源利用和经济发展的比值(α±1,t)用供水量与需水量的比重表示,并进一步得到相应协调度(μ±A1(α1,t))的表达式:
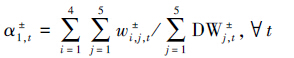
|
(13) |
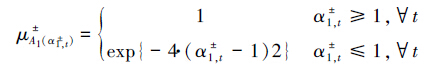
|
(14) |
式中,A1为区域水资源利用与经济效益的模糊子集.
同理,区域经济发展与水资源质量改善程度的比值(α±2,t)可通过式(15)表示,并得出相应协调度(μ±A2(α2,t))的表达式:
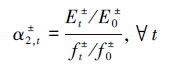
|
(15) |
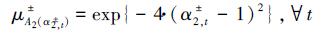
|
(16) |
式中,Et和E0分别为区域t时期和基准年的水资源利用经济效益(元);ft和f0分别为区域t时期和基准年的COD排放量(t);A2为区域经济效益与水体改善的模糊子集.
最后,引入“区域协调发展指数(μt±)”以同时表征前述的水资源利用与经济发展、经济发展与环境质量改善这两方面的协调度,具体如下:
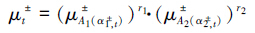
|
(17) |
式中,r1、r2为指数权重,文中取r1=r2=0.5.
3.3 下层调度优化模块 3.3.1 目标函数下层以配水量最小化为目标函数,其规划目的是在保障社会经济发展的前提下,减少水资源的使用量:
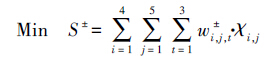
|
(18) |
式中,S为规划期内系统取水总量(m3).
3.3.2 约束条件下层约束条件主要涵盖水资源承载力、部门供需水量要求、变量非负约束等方面,具体如下.
水资源数量承载能力约束:各部门需水量不能大于供水源的供给能力(式(19)).
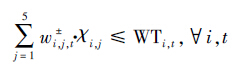
|
(19) |
水资源质量承载能力约束:各部门在利用水资源过程中所排放的COD量不能大于地区所允许的COD最大排放量(式(20)).
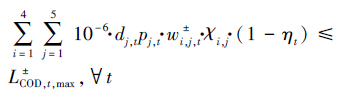
|
(20) |
部门用水供需约束:部门的需水量不是一成不变的,需要确定各部门的最小和最大需水量.模型中引入最低和最高需水系数来体现部门的需水要求,其中,最低需水系数与预测需水量的乘积代表最小需水量,最高需水系数与预测需水量的乘积代表最大需水量(式(21)).
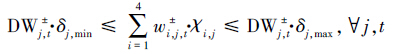
|
(21) |
变量非负约束:要求模型决策变量的取值须大于等于零(式(22)).
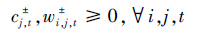
|
(22) |
式中,WTi,t为t时期i水源的可供水量(m3);DWj,t为t时期j用户的用水需求(m3);δj,min和δj,max分别为j用户最低和最高需水系数,文中分别取0.9和1.0;pj,t为t时期j用户的COD排放系数;ηt为t时期COD去除率;LCOD,t,max为t时期COD最大允许排放量(t).
3.4 模型参数确定 3.4.1 经济和环境参数获取参考城市排水工程规划和丰台区污水排放现状,选取农业、工业、三产、生活和生态环境的污水排放系数分别为0.1、0.5、0.7、0.7和0.8,相应污水中的COD分别为[55,60]、[90,100]、[110,120]、[215,230]和[25,30] mg·L-1.依据用户万元产值取水量的倒数确定不同需水部门的效益系数,本文的效益系数主要是参考相关文献资料(叶健等,2012)而获得.通过选取临近地区的供水效益系数,可以使模型更具典型性和代表性,具体取值如表 1所示.
| 表 1 区域供水效益系数 Table 1 Effectiveness coefficient of water supply |
区域的需水预测主要依据指标分析法,即根据各部门的用水影响因素(灌溉面积、工业产值、人口数量等)及用水定额进行预测(杜芙蓉等,2009),具体公式如下:
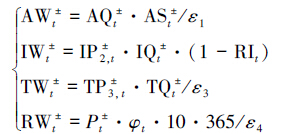
|
(23) |
式中,AWt、IWt、TWt和RWt分别为t时期农业灌溉需水量、工业需水量、第三产业需水量和城市生活需水量(m3);AQt为t时期灌溉定额(m3·hm-2);ASt为t时期灌溉面积(hm2);ε1、ε3和ε4分别为渠系水利用系数、工业供水系统水利用系数和城市生活用水利用系数,模型中分别取值0.8、0.8和0.9;IPt和TPt分别为t时期工业和第三产业产值(万元);IQt和TQt分别为t时期工业和第三产业万元产值用水定额(m3·万元-1);RIt区域t时期工业用水重复利用率,目前,我国工业水资源的重复利用率仅为25%,参照现状水平,3个规划期工业水重复利用率分别设定为25%、30%和32%;Pt为t时期人口数量(万人);φt为区域t时期人均日用水量(L·人-1·d-1).
4 算例分析(Case study) 4.1 算例概述选取北京市丰台区作为研究对象,该区位于北京市西南部,总面积305.8 km2.根据2000年《丰台区水资源评价》的计算结果,全区多年平均水资源总量达到1.2×108 m3,人均水资源占有量为65 m3,远低于北京市120 m3的平均水平.全区的供给水源主要来自于本地地表水、地下水、再生水和客水.截止2013年,全区共计5座供水厂,总供水能力为3.1×104 m3·d-1;正在运行的4座再生水厂,另外的卢沟桥和小红门再生水厂正在建设中,预计“十三五”期间投入使用,全区再生水利用能力将达到17.0×104 m3·d-1;由于气候因素和河流断流影响,全区地下水资源补给量锐减,地下水处于超采状态,地下水位处于连年下降趋势(年均下降1 m);客水主要考虑南水北调水源,南水北调中线主干线和南干线均穿过丰台区,并为丰台区内的长辛店水厂和郭公庄水厂两座大型水厂供水,使丰台区新增供水能力30.0×104 m3·d-1,届时,将很大程度上改善全区缺水的态势.结合丰台区水资源利用现状和规划期内的不确定性因素,表 2列出了规划期内丰台区的各水源供给能力.另一方面,由于不合理的用水结构和低效的污水处理能力,区内的水环境质量不容乐观,主要河流现状水质类别均为劣Ⅴ类,均不符合相应功能水质标准.
| 表 2 丰台区各水源供给能力 Table 2 Water supply capacity in Fengtai District |
根据丰台区第一次水务普查公告和历年统计年鉴,2011年,全区经济社会年度用水总量达到145.50×106 m3.其中,农业用水量达到5.83×106 m3,占总用水量的4.0%,农业灌溉面积为5273 hm2,每公顷的灌溉用水量约为1105 m3·hm-2;工业用水量为14.94×106 m3,万元工业产值用水量为30.0 m3·万元-1;第三产业用水量为31.00×106 m3,万元三产产值用水量基本达到5.0 m3·万元-1;城市生活用水量为87.40×106 m3,常住人口达217.0万人,人均用水水平为110.0 L·人-1·d-1;生态环境需水主要考虑城市绿化和河湖生态用水,2011年丰台区城市绿化用水仅占总用水量的2%;河湖面积约为228 hm2,河湖生态需水量共计74.00×106 m3.考虑到丰台区水资源利用现状,生态需水在规划期内将难以保证充分供给.
以2011年丰台区的现状用水水平为参照,依据用水总量控制、城市生活用水适当增加、工业用水基本维持、农业用水零增长或负增长、生态环境用水增加的原则,确定各部分的用水定额,最终预测得到各规划期内的部门需水量,具体如表 3所示.由表 3可得,城市生活是最大的需水部门,其需水量约占所有部门总需水量的45%;近几年丰台区加快了生态城市建设步伐,因此,生态环境需水量所占份额明显提高;由于第三产业是丰台区的经济主体,其水资源占有量在生产用水总量中是最大的,而农业用水则呈现逐年下降趋势,这主要是由于农业灌溉面积和灌溉定额的减少;从水资源供需方面分析,在南水北调工程正式开通后,区内总体缺水并不严重,3个规划期的理论缺水量将分别达到[0.34,0.80]×106 m3、[0.38,8.01]×106 m3、[9.43,16.49]×106 m3.
| 表 3 丰台区需水量预测 Table 3 The prediction of water demand in Fengtai District |
在分析丰台区水资源供需的基础上,考虑供水量小于需水量和时空分配不均的现状,并根据区域社会经济可持续发展要求,构建了水资源双层管理模型.表 4为水资源优化配置方案,结果以区间值表示.由表可知:3个规划期内,丰台区的配水总量分别达到[232.21,279.39]×106 m3、[258.43,329.78]×106 m3和[300.20,361.15]×106 m3.从供水源分析:本地地表水和客水(南水北调水源)是丰台区主要的供给水源,两者的供水量约占总量的75%;而地下水主要供给城市生活用水,再生水全部用于生态环境用水.从缺水程度分析:丰台区各规划期内的部门供需水量基本达到平衡,但依然存在少量缺水现象,其中,生态环境缺水程度最高.造成丰台区缺水的主要原因在于:①相对于城市的快速发展,供水量仍相对不足,其中,第三产业的需水增长速度尤为明显;②由于配水管理政策限制,部分水源只能给特定部门供水,而造成其他部门出现缺水现象.从节水角度考虑,城市生活、生态环境和第三产业是丰台区的水资源消耗主体,其中,生态环境需水相对恒定.所以,全区可以通过控制人口规模和产业升级来提高水资源利用率.
| 表 4 规划期内水资源优化配置结果 Table 4 Optimal allocation of water resources in planning horizon |
根据净水价格构成机制和水资源管理系统中社会经济协调发展需求,表 5给出了各规划期内不同用水部门的净水价格和污水处理费用的优化结果.水资源管理系统的上层决策者通过制定合理的净水价格和污水处理费用来影响用水部门的取水量,从而影响区域经济发展水平.较高的水价可以防止水资源过度使用,从而降低资源与环境压力,但会导致水资源经济效益的削减;反之,较低的价格容易增加水资源利用量从而提高经济效益,但往往忽略了资源与环境的承载力.在区域水资源配置系统中,可以通过价格的市场调节作用来改善区域的水资源利用与经济的协调发展.在丰台区水资源管理的不确定双层规划模型中引入了水环境-经济协调发展约束(其值要求不小于0.8),其目的就在于协调丰台区水资源利用、经济效益与水体改善之间的矛盾关系.丰台区水资源-经济协调性分析结果表明:在保证区域水资源供需比在90%以上的前提下,优化配水量与预测需水量的比例,系统协调度μ±A1的优化值均高于0.95,说明丰台区水资源开发利用与经济效益具有很好的协调性;而μ±A2也超过了0.80,反映了该地区的水资源经济效益与环境改善具有较好的协调性;区域总体协调发展指数(μ±t)的优化值在0.82~0.92之间,说明规划期内丰台区水资源管理系统的社会、经济、环境处于协调发展之中.第一时期与第三时期相比,总体协调发展指数有上升趋势,说明丰台区水资源系统的管理成效具有可持续性.
| 表 5 净水价格和污水处理费用优化结果 Table 5 Solutions of water price and sewage treatment cost |
图 2和图 3分别展示了水资源管理系统的经济效益和相应的COD排放量.优化结果表明:丰台区水资源管理系统3个规划期内的系统经济效益分别达到[5.52,13.79]×108元、[7.58,18.60]×108元和[9.08,19.26] ×108元;相应的COD排放量分别为[4388,5605] t、[4835,6440] t和[5430,6811] t.另一方面,系统满意度(λ)是权衡系统经济效益和配水量关系的重要因子.模型优化结果显示,λ值为[0.75,0.81],说明双层优化结果较好.
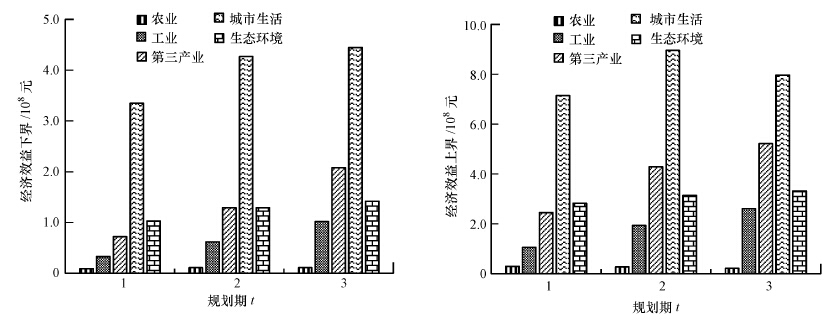 |
| 图 2 规划期内的系统经济效益 Fig. 2 System economic benefit in planning horizon |
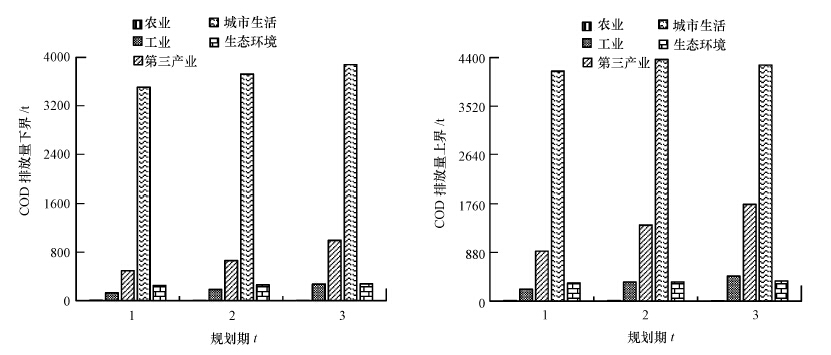 |
| 图 3 规划期内的COD排放量 Fig. 3 COD discharged in planning horizon |
在IBPM-WRM中主要考虑经济效益模块和水资源调度模块,但在水资源管理系统中,水体污染物控制是不可回避的问题.因此,需要开展水体污染物(主要考虑COD排放)不同排放控制要求下的系统规划研究.本文设计4种COD最大允许排放情景,其中,情景A为IBPM-WRM中的COD最大允许排放值,而情景B、C和D依次对COD最大允许排放量加以进一步限制,具体如表 6所示.
| 表 6 不同情境下的COD最大允许排放量 Table 6 Maximum COD allowable emissions under different situations |
图 4为不同情景下的系统经济效益和COD排放量.由图可知,在整个规划期内,情景A、B、C和D的系统经济效益分别为[2.22,5.16]×109元、[2.20,5.12]×109元、[2.18,5.02]×109元和[2.06,4.99]×109元.由此可见,较低的COD最大允许排放量会削减系统经济效益.另一方面,在整个规划期内,情景A、B、C和D的COD排放量[1.47,1.89]×104 t、[1.44,1.87]×104 t、[1.42,1.81]×104 t和[1.38,1.79]×104 t.总体而言,不同的COD排放约束会对模型的规划结果产生重要影响.
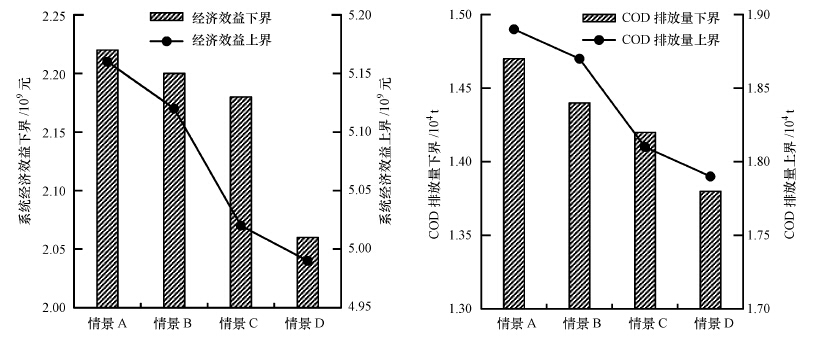 |
| 图 4 不同情景下的系统经济效益和COD排放量 Fig. 4 Economic benefit and COD discharged under different situations |
分别以上层和下层目标为主要目标函数,建立两个传统的单目标优化模型:①以系统经济效益最大化为主要目标的不确定性水资源规划模型(IPM-WRM1);②以取水量最小化为主要目标的不确定性水资源规划模型(IPM-WRM2).将两个传统单目标优化模型与双层优化模型进行对比,结果如表 7所示(其中,水资源供需比取上界和下界优化结果的平均值).结果表明:IPM-WRM1仅从经济效益角度出发,其优化结果会得到最高的配水量和最高的经济效益,各个部门的供需比也达到最高要求,但同时带来最高的COD排放量;而IPM-WRM2仅从节水角度出发,所以其优化结果中的COD排放量、经济效益和配水量是最低的,部门的供水也按最低供需比进行配给;IBPM-WRM则同时兼顾经济因素和节水要求,其优化结果可以为不同层面的决策者提供更加合理的水资源分配方案、系统管理效益、COD控制方案和部门需求要求.总体而言,IPM-WRM1的优化方案适用于力求区域经济高速发展的情景;IPM-WRM2的优化方案体现保护水源和改善水质要求;而当同时兼顾经济效益、水源保护和水质改善时,IBPM-WRM的优化结果是一种切实的方案.
| 表 7 三种模型优化方案对比 Table 7 Solution comparisons of three models |
1) 采用指标定额法预测丰台区规划期内的需水量,预测结果表明,在南水北调工程正式开通后,全区的水资源供需基本达到平衡状态.
2) IBPM-WRM能够反映复杂系统的多目标、多层次和多决策者的特征和交互影响,本文将其应用于北京市丰台区水资源管理系统.在模型构建中引入区间参数表征系统的不确定信息,双层规划则用于处理水资源管理者和使用者之间的层次关系.
3) 结合交互式算法和模糊满意度算法,利用Lingo编程软件对IBPM-WRM进行求解,可以得到经济效益、配水量、COD排放量和系统满意度(λ)的优化结果.结果表明:本地地表水和南水北调水源将是丰台区主要的供给水源,两者的供水量约占总量的75%;规划期内的系统经济效益预期达到[2.22,5.16]×109元,COD排放量将达到[1.47,1.89]×104 t;λ则是权衡经济效益和配水量关系的重要因子,其值为[0.75,0.81].
4) 通过设计4种不同的COD最大允许排放情景,说明了不同的COD排放约束将对丰台区水资源管理系统的经济效益和环境影响产生重要影响;同时,通过3种模型规划结果的对比分析,能够为决策者提供多情景下的决策方案.
| [1] | 北京市丰台区水务局. 2011.丰台区"十二五"时期水资源保护与节约利用规划[R].北京:北京市丰台区水务局 |
| [2] | Calvete H I, Galé C. 2010.Linear bi-level programs with multiple objectives at the upper level[J]. Journal of Computational and Applied Mathematics, 234 (4): 950–959. |
| [3] | 戴国瑞, 冯尚友. 1983. 水资源科学分配[M]. 武汉: 水利电力出版社 . |
| [4] | 邓彩琼.2005.区域水资源优化配置模型及其应用研究[D].武汉:武汉大学 |
| [5] | 杜芙蓉, 杜长胜.2009.焦作市需水预测与水资源优化配置研究[J].水电能源科学, 27 (4):25–28. |
| [6] | Hathhorn W E, Tung Y K. 1989.Bi-objective analysis of waste load allocation using fuzzy linear programming[J]. Water Resources Management, 3 : 243–257. |
| [7] | He L, Huang G H, Lu H W. 2011.Greenhouse gas emissions control in integrated municipal solid waste management through mixed integer bi-level decision-making[J]. Journal of Hazardous Materials, 193 : 112–119. |
| [8] | Huang G H, Baetz B W, Parry G G. 1992.A grey linear programming approach for municipal solid waste management planning under uncertainty[J]. Civil Engineering Systems, 9 (4): 319–335. |
| [9] | Kasperski A. 2005.A possibilistic approach to sequencing problems with fuzzy parameters[J]. Fuzzy Sets and Systems, 150 : 77–86. |
| [10] | 刘昌明, 何希吾. 1996. 中国21世纪水问题方略[M]. 北京: 科学出版社 . |
| [11] | 李婷贤.2013.基于双层规划的区域水资源优化配置问题研究[D].青岛:山东科技大学 |
| [12] | 刘三省, 尹建光, 李薇, 等.2014.基于区间机会约束规划的滨州新区水资源优化配置[J].水电能源科学, 32 (7):28–32. |
| [13] | Lu H W, Huang G H, He L. 2009.An inexact programming method for agricultural irrigation systems under parameter uncertainty[J]. Stochastic Environmental Research and Risk Assessment, 23 : 759–768. |
| [14] | Li M, Guo P. 2014.A multi-objective optimal allocation model for irrigation water resources under multiple uncertainties[J]. Applied Mathematical Modelling, 38 : 4897–4911. |
| [15] | 莫淑红, 段海妮, 沈冰, 等.2014.考虑不确定性的区间多阶段随机规划模型研究[J].水利学报, 45 (12):1427–1434. |
| [16] | Shih H S,Lee E S.1999.A fuzzy possibilistic approach to multi-level optimization[C].The Eighth Annual Industrial Engineering Research Conference.23-26 |
| [17] | 吴丹, 吴凤平.2012.基于双层优化模型的流域初始二维水权耦合配置[J].中国人口·资源与环境, 22 (10):26–34. |
| [18] | Xu J P, Tu Y, Zeng Z Q. 2013.Bilevel optimization of regional water resources allocation problem under random environment[J]. Journal of Water Resources Planning and Management, 139 : 246–264. |
| [19] | 叶健, 刘洪波, 闫静静.2012.不确定模糊多目标模型在生态城市水资源配置中的应用[J].环境科学学报, 32 (4):1001–1007. |
| [20] | 于森, 蒋洪强, 常杪, 等.2015.松花江流域水资源-水污染联合调控方案动态模拟研究[J].环境科学学报, 35 (6):1866–1874. |
| [21] | 张静, 黄国和, 刘烨, 等.2009.不确定条件下的多水源联合供水调度模型[J].水利学报, 40 (2):160–165. |
| [22] | Zheng Y, Wan Z P, Wang G M. 2011.A fuzzy interactive method for a class of bilevel multiobjective programming problem[J]. Expert Systems with Applications, 38 (8): 10384–10388. |
 2016, Vol. 36
2016, Vol. 36


