石煤是我国一种重要的优势含钒资源，在我国的储量占国内V₂O₅总储量的87%，从石煤中提取钒是获得V₂O₅的重要途径(Zhang et al., 2011).随着石煤提钒行业的发展，其生产规模在不断扩大.但我国部分石煤提钒企业面临资源利用率低、工艺不成熟、设备配置落后、染严重等技术问题.目前需要对各类工艺从清洁生产的角度进行横向对比，帮助企业实现“自我评估，发现问题，制定方案”.笔者曾以生命周期评价理论(LCA)为基础，对石煤提钒行业清洁生产工艺及评估进行了深入研究，建立了该行业清洁生产评价指标体系及标准，并应用AHP-Fuzzy综合评价模型对企业生产工艺清洁性进行了评价(李佳等，2013a;2013b).但该方法在后期现场应用中出现两方面问题：第一，方法中赋权选用的是层次分析法(AHP)，主要依托专家的经验和知识确定各因素相对重要性，评价结果具有较大的主观性和随机性；第二，个别企业认为现场操作较为繁琐，可操作性差.因此，研究一套科学、合理、易操作的石煤提钒清洁生产工艺评价方法，是石煤提钒生产工艺面临的一个重要问题.

传统的清洁生产评价方法，如层次分析法(张燕燕等，2010)、单因子评价法(Tadeusz et al., 2007)等在应用过程中虽然操作过程简单，但由于以定性或半定性半定量分析为主，存在主观成分较多，分类能力差的问题(Barbiroli et al., 2003;杜栋等，2008).随着人工智能技术的发展，已有学者成功运用人工神经网络(张旭等，2009)、贝叶斯分类(滕丽华等，2008)等机器学习方法进行清洁生产评价.鉴于石煤提钒工艺的特征，评价指标较多，样本数量有限，因此，要考虑小样本、高噪声、非线性及模糊性的数据特点(Li et al., 2014).这类基于小样本的评价问题在现实中是广泛存在的，而数据挖掘技术中的支持向量机方法在样本量需求上占有优势(杨力等，2011).支持向量机(Support Vector Machine，简称SVM)评价方法是利用有限的样本数据在模型的复杂性和学习能力间寻求最佳平衡，从而在统计样本数量较小的情况下以求获得最好的泛化能力(张玉超等，2009).SVM方法目前广泛应用于银行信用风险(Sun et al., 2006)、地质灾害评估(Bui et al., 2012)、湖泊生态系统评价(毕温凯等，2012)等方面，而利用SVM进行清洁生产评价的研究还鲜见报道.在SVM的应用过程中发现，SVM的参数选取是影响SVM学习能力和泛化能力的关键问题(Marjanović et al.， 2011)，SVM学习方法本身在参数选取方面是通过经验及反复实验对比而获取，存在事件性及主观性的缺点.因此，在使用SVM的评价功能方面，必须根据所要评价的对象特征选择合适的方法对SVM进行优化.

鉴于遗传算法(GA)作为一种可用于复杂系统优化计算的搜索算法，在寻求搜索问题最优解方面具有优势(齐珺等，2008).因此，本研究拟利用GA对SVM的核函数及其参数选择进行优化，根据石煤提钒3种工艺类型，分别建立基于GA-SVM的石煤提钒工艺清洁生产评价模型，并将该模型分别应用于生产工艺评价中，旨在更客观、科学地表征工艺清洁生产水平，为该行业可持续发展提供理论指导和有效的评价工具.

笔者在前期对石煤提钒工艺进行了深入研究，根据矿石中钒的赋存状态，将石煤提钒工艺归纳为3类，即水浸工艺、弱酸浸工艺和强酸浸工艺.水浸工艺、弱酸浸工艺包括预处理、焙烧(钠化焙烧、钙化焙烧、空白焙烧、复合添加剂焙烧)、浸出(水浸、酸浸)、净化富集(萃取法、离子交换法)、精钒制取(水解沉钒煅烧、铵盐沉钒煅烧)5个阶段，强酸浸工艺流程不包含焙烧阶段.同时，以生命周期评价理论(LCA)为基础，根据3种石煤提钒工艺类型，构建了石煤提钒工艺清洁生产评价指标体系，分别为5个一级定量指标及所属的19~23个二级指标(其中，水浸/弱酸浸工艺23个指标，强酸浸工艺19个指标)，2个一级定性指标及所属的6个二级指标，并将清洁生产水平等级划分为3级，不同的工艺类型对应不同的各项指标标准值(Li et al., 2014).本研究将以此为基础做进一步评价方法研究.

根据支持向量机最小样本量的要求，按照石煤提钒工艺类型(水浸工艺、弱酸浸工艺、强酸浸工艺)，分别选取3家企业进行现场数据采集及验证工作，最终形成30组数据作为训练样本，20组数据作为测试样本.

根据所确定的石煤提钒工艺清洁生产评价等级标准，以Matlab7.0为平台，选用r and s()函数(金菊良等，2002)进行计算.因为不同指标上下限分别确定了不同的等级，因此，以这些指标生成序列和其所属的评价等级值构成建模序列.设第n个评价等级中评价指标取值的下限和上限分别为a_jⁿ和b_jⁿ，y_jⁿ为其相应的评价等级，则评价指标随机模拟公式为：

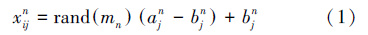
根据3家企业特点，设计采集方案，主要对工艺流程(工艺参数/指标)、主要污染防治设备及操作运行条件、产生污染物情况(污染物组成、控制限制、排放量等)、环保投资(一次投资与运行维护成本)、污染处理设施运行情况(净化效率、操作条件等)、废物循环与资源化利用等方面进行全面数据采集.整个采集工作采用查阅台账、查阅现场计量设备参数与现场取样分析监测相结合的方法进行.由于各企业采用的工艺不完全相同，因此，具体的方案也存在一定的差异.每次现场数据采集时均选择企业连续正常运转3天的情况进行取样分析，再针对相应的指标要求折算到全年进行计算. 2.2.3 数据预处理 上述来源于企业现场操作及实验室采集和存储的大量各类数据具有不完整性、噪声性和不一致性，不符合后期具体算法进行知识获取研究所要求的质量和标准，因此，需要通过数据清理、数据变换.本研究基于MATLAB 平台，选取比例转换法，使用MATLAB 自带的数据归一化函数mapminmax 实现原始数据归一化计算，根据支持向量机最小样本量的要求，按照所划分的石煤提钒工艺类型，最终对3种工艺分别整理30组训练样本和20组测试样本.

SVM是由Vapnik(1998)根据统计学理论提出的一种新型的机器学习方法，该方法用途分为两大类(张成成等，2013)：分类和回归.由于本文主要采用其分类功能，且鉴于所评价的石煤提钒工艺指标体系数据的非线性特点，将重点介绍所运用的非线性可分支持向量机模型.

SVM用于分类的基本思想是(李湘梅等，2008)：通过求解凸二次规划问题，寻找一个最优超平面，使它能够尽可能多地将两类数据点正确地分开，同时使分开的两类数据点距离分类面最远.设在D维空间有训练集T={(x_i，y_i)︳i=1，2，…，l}，其中，x_i∈Rⁿ，y_i∈{1，-1}，分类超平面为wx+b=0(w为分割平面的法向量，b为分割平面的偏移量).这个平面就是将训练数据集中分类，所以最大化间隔可转化为如下最优化数学模型：

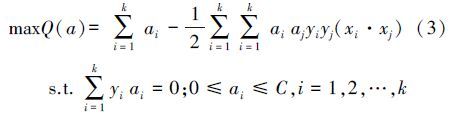
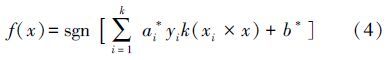
对于非线性SVM，可将原始线性不可分数据映射到高维特征空间，在特征空间运用内积函数实现线性不可分数据集的分类.

假设利用核函数K x_i·x_j =Φ x_i ·Φ x_j 将原始数据映射到高维特征空间，那么特征空间的核函数SVM为：

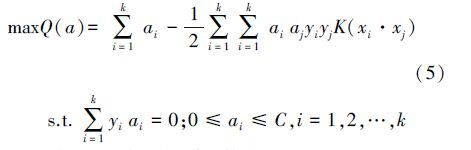
式(5)对应的判别函数为：

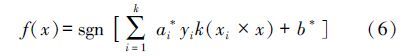
空间的核函数SVM为：

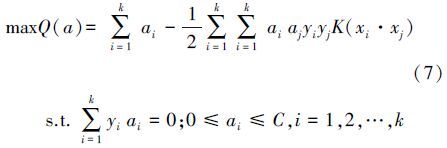
式(7)对应的判别函数为：

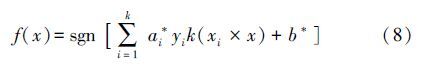
由式(8)可看出，核函数K(x_i，x_j)取代了K(x_i，x_j)=Φ(x_i)·Φ(x_j)，巧妙地解决了传统机器学习方法中“维数灾难”的问题.根据上述理论，在不需要知道映射转化具体形式的情况下，只要选取合适的核函数K(x_i，x_j)，则可避开高维变换的线性问题，将问题简化.而一个函数是核函数的充要条件是满足Mercer定理，而满足Mercer定理的核函数很多，核函数的不同所构造的SVM不同，常用的核函数包括线性核函数(式(9))、多项式函数(式(10))、径向基函数(RBF)(式(11))、Sigmoid核函数(式(12)).核函数及参数对SVM的性能影响较大，因此，在应用前需要进行核函数对比及优化设置.

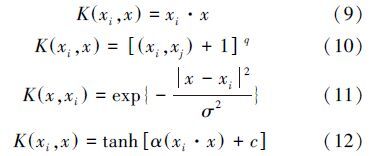
本研究根据石煤提钒工艺特点及样本采集数据量，利用二进制编码方式对SVM的模型参数进行遗传编码，提出GA优化SVM参数的具体步骤如图 1所示.

图1(Fig.1)

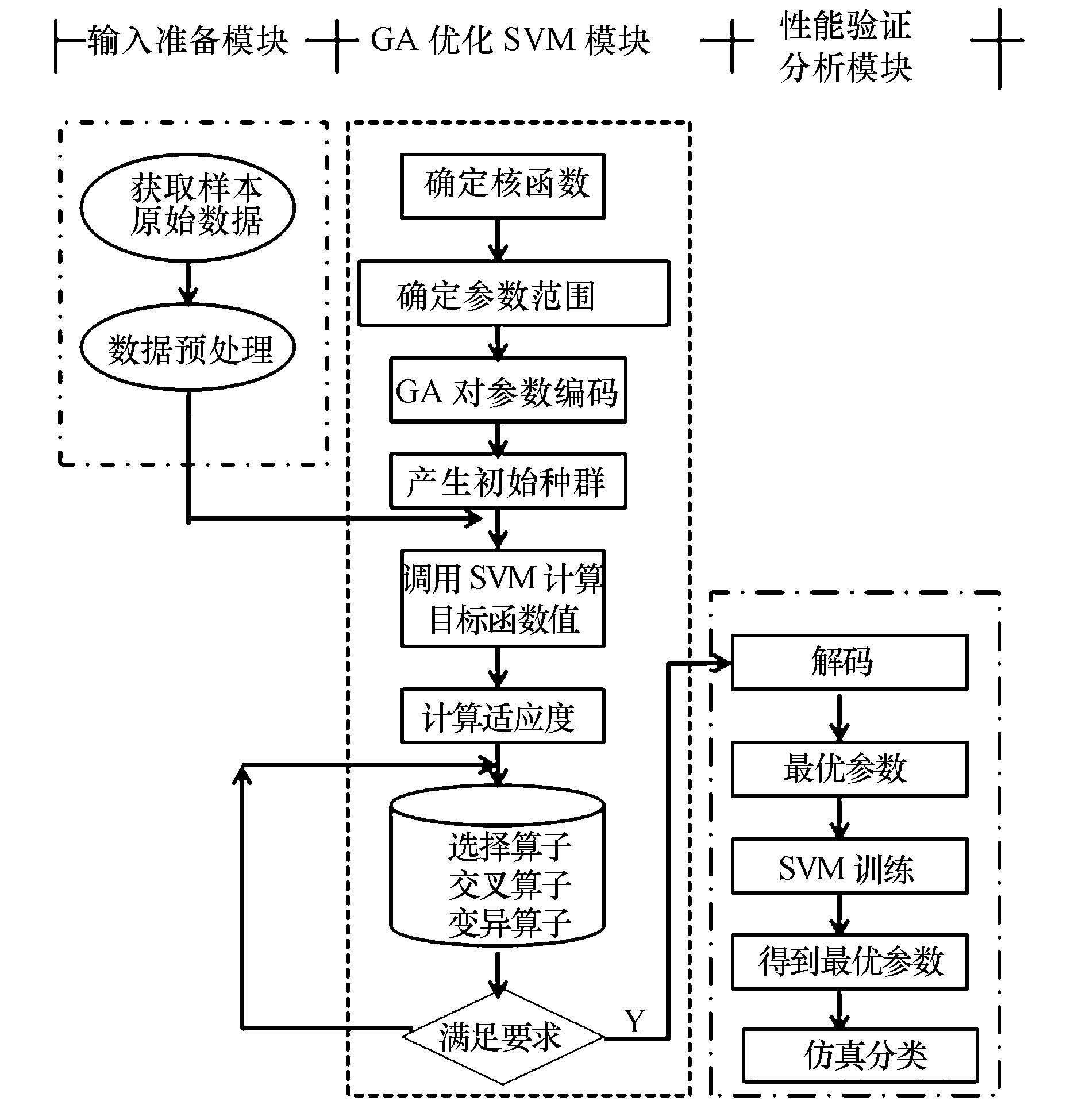图1 GA-SVM 优化模型应用步骤 Fig.1 GA-SVM application steps

本研究评价方法的应用过程使用MATLAB7.8为操作平台，运用LIBSVM2.89软件实现.

本研究分别选取4种核函数(6类)，分别是线性、多项式(d分别取1、2、3)、RBF、Sigmoid，主要研究在不同训练样本比率、不同核函数条件下的分类准确性，以期选择分类较为准确的核函数作为仿真条件.6类核函数在8组计算中的各类样本平均正确率见表 1.从表 1的平均正确率可看出，RBF函数的分类效果较其它函数要好，同时说明同一类核函数在参数不同时，分类结果会相差比较大.

表1(Table 1)

表1 不同训练样本下的平均分类正确率(C-SVM) Table 1 Average classification accuracy rate under different training samples(C-SVM)

表1 不同训练样本下的平均分类正确率(C-SVM) Table 1 Average classification accuracy rate under different training samples(C-SVM) 核函数 平均正确率(C-SVM) 训练 测试 线性 85.30% 82.40% 多项式(d=1) 86.80% 80.80% 多项式(d=2) 84.10% 85.20% 多项式(d=3) 88.30% 79.20% RBF 92.70% 89.20% Sigmoid 82.70% 81.20%

根据GA-SVM模型建立思路，下面进行核函数参数的选取步骤.

一般建议取值数目为20~100.本研究先取30作为种群数量，以强酸浸工艺样本为例测试输出的种群个体适应度(图 2a).由图 2a可看出，在种群数目为10附近，所测试输出的种群个体适应度已可达到100%，一直平稳维持直到在种群数目为24附近，出现不稳定现象，平均值适应度为91.4%.因此，本研究取20作为种群数量(即根据20组不同的C和g值最后选择最大值所对应的最佳值)，测试输出的种群个体适应度，以强酸浸工艺样本为例，结果如图 2b所示.可以看出，20个种群都有一个适应度，其中，20个适应度的最大值为100%，平均适应度为95%.

图2(Fig.2)

图2 种群个体适应度值随种群数目变化示意图(a.30个种群，b.20个种群) Fig.2 Sketch of individuals fitness values as a function of population

根据所确定的RBF径向基核函数，所需确定的参数包括核函数参数g和惩罚参数C.考虑到当前仿真中的类别数为3，因此，设置g和C分别在[0.01，100]和[0，500]，种群数量为20的条件下进行SVM分类方法的参数优化，这样便可以在较短时间内搜索到全局最优点. 3.2.3 遗传终止迭代条件设置 一般预设的代数设置为50~500代.以强酸浸工艺为例，本研究设置最大的进化代数为200，终止条件为最佳适应度大于等于95%，并且迭代小于最大迭代的1/2，并且最大进化代数为200的适应度和前面一代的最佳适应度之差小于1%，运行结果见图 3.由3可看出，进化代数>20时，平均适应度就已经达到了95%，而代数为100时，进化代数便终止了，因此，选择200作为最大的迭代次数，留有一定的余量是合理的.

图3(Fig.3)

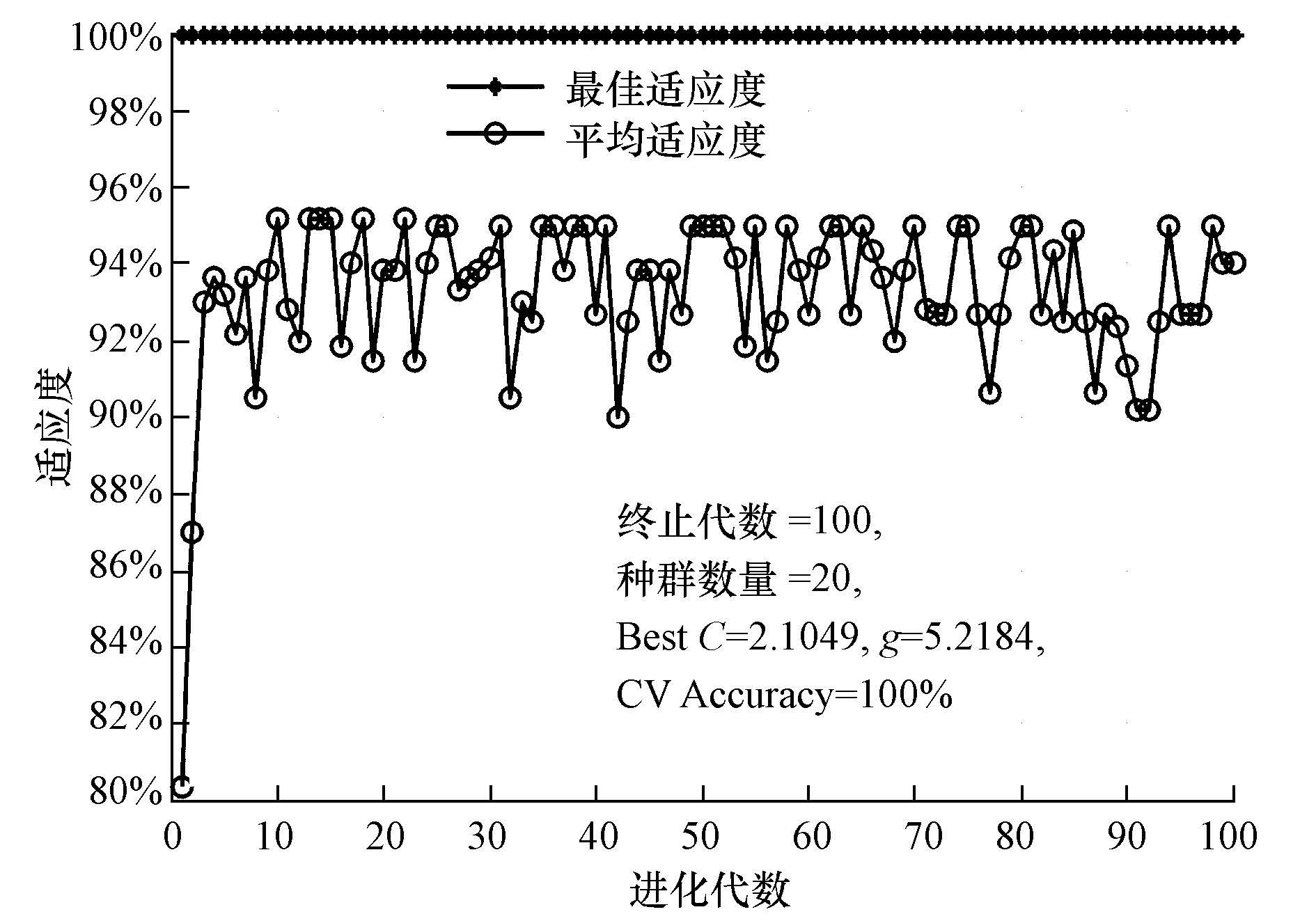图3 GA确定参数结果分析(强酸浸工艺) Fig.3 GA determined parameter results analysis for strong acid leaching process

在确定以上核函数及核函数参数取值范围后，通过GA算法对训练样本进行全局寻优，同时利用网格搜索法确定参数区间，并利用交叉验证思想，对优化参数进行校验.以强酸浸为例，GA算法参数寻优结果见图 3，最终确定出强酸浸最优惩罚因子C和核函数参数g，分别为Best C=2.1049，g=5.2184.交叉验证结果见图 4，图中颜色较深平面为分类效率较高平面，交叉验证结果表明，GA算法参数寻优所得参数值在交叉验证最高分类效率平面内；同理，弱酸浸工艺为Best C=0.0035286，g=1.9947；水浸工艺为Best C=0.39587，g=1.4105.

图4(Fig.4)

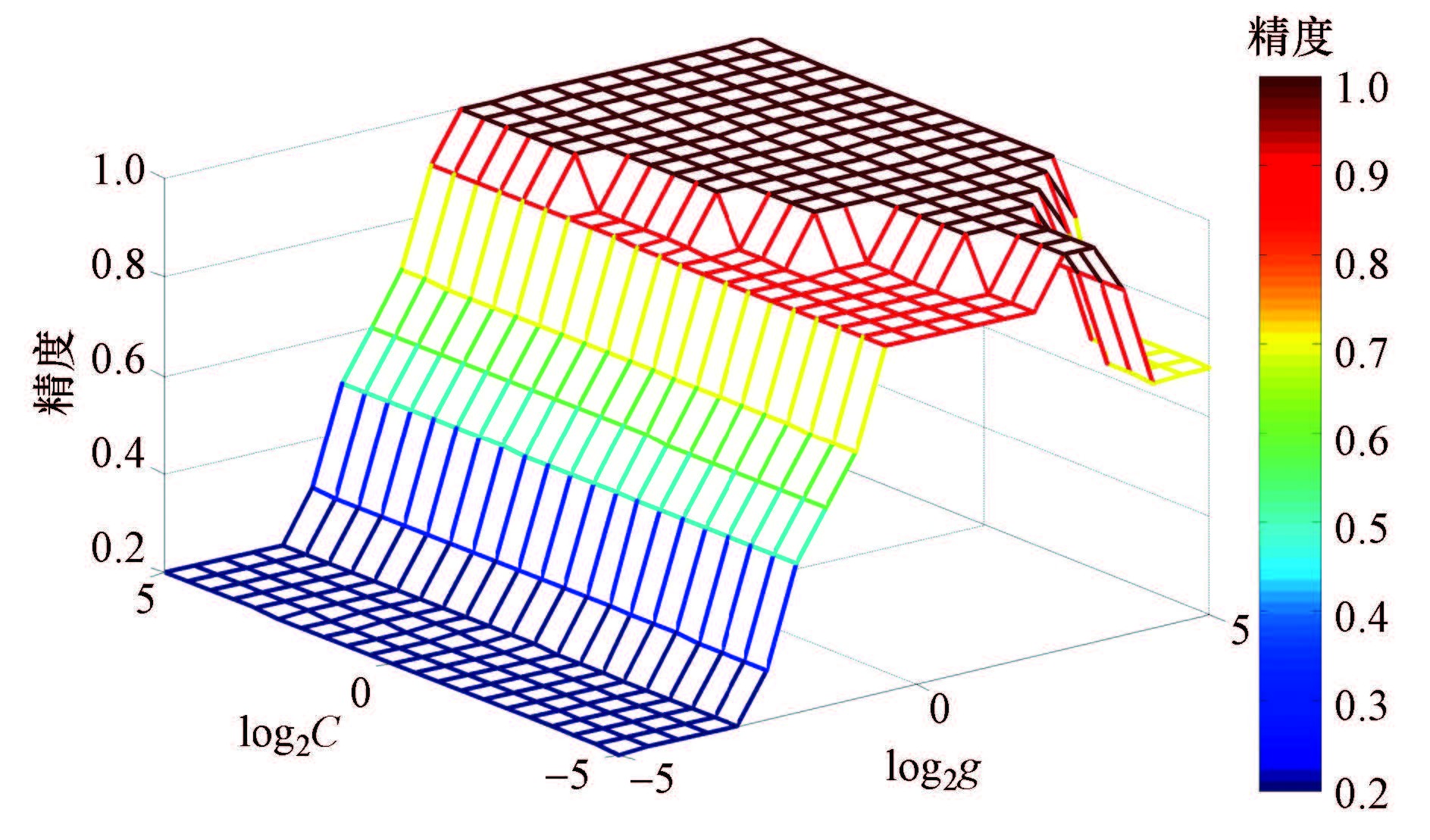图4 模型参数寻优结果 Fig.4 Optimization of model parameters

通过上述相关条件的设置，对GA-SVM方法进行样本收敛曲线测试验证，结果如图 5所示.由图 5可以看出，随着输入数据的增加，误差越来越小，最后训练、验证、测试的均方误差都小于10^-6，效果比较好，在第25次迭代时，验证的最好性能达到了10^-7的均方误差.

图5(Fig.5)

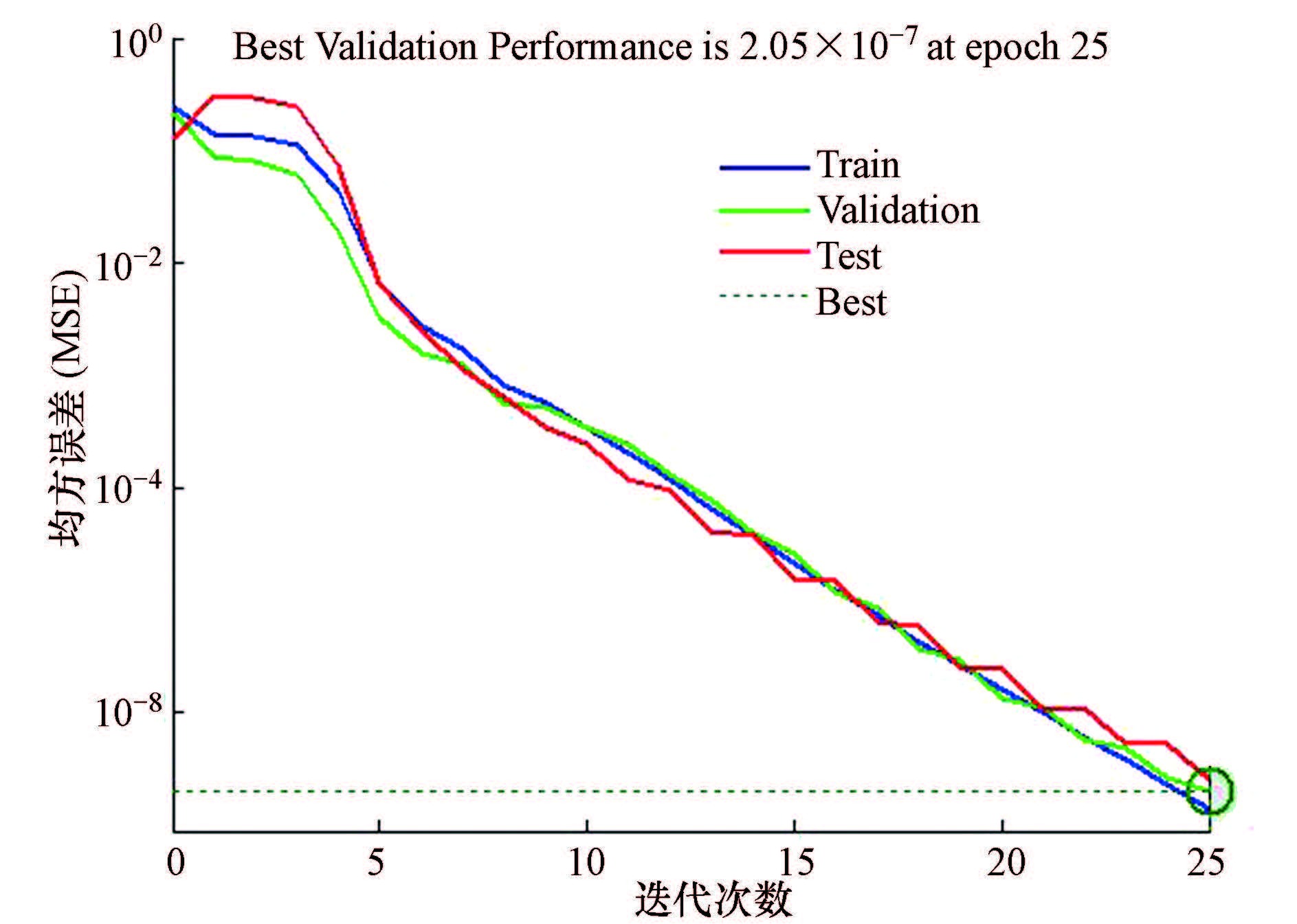图5 GA-SVM样本收敛曲线 Fig.5 Convergence curves of GA-SVM samples

以强酸浸工艺为例，通过训练样本，以验证选用的GA寻优的有效性，以及GA-SVM方法的准确性和可操作性.当计算结果输出值为1时，表示受检工艺为淘汰水平；当计算结果输出值为2时，表示受检工艺为一般水平；当计算结果输出值为3时，表示受检工艺为先进水平.

根据GA得到的最优核函数参数及惩罚因子，将训练样本数据代入GA-SVM评价方法中，评价结果见图 6.由图 6可以看出，基于GA优化参数的SVM方法，经强酸浸工艺30组样本训练后，评价结果为7个样本是先进工艺水平，7个样本为一般工艺水平，6个样本为淘汰工艺水平，评价结果与实际工艺水平是相符的，预测测试精度达到了100%.验证结果表明，本研究利用GA的全局寻优能力搜寻到参数最优组合，使得SVM分类方法在石煤提钒工艺清洁生产评价中取得较好的验证效果.

图6(Fig.6)

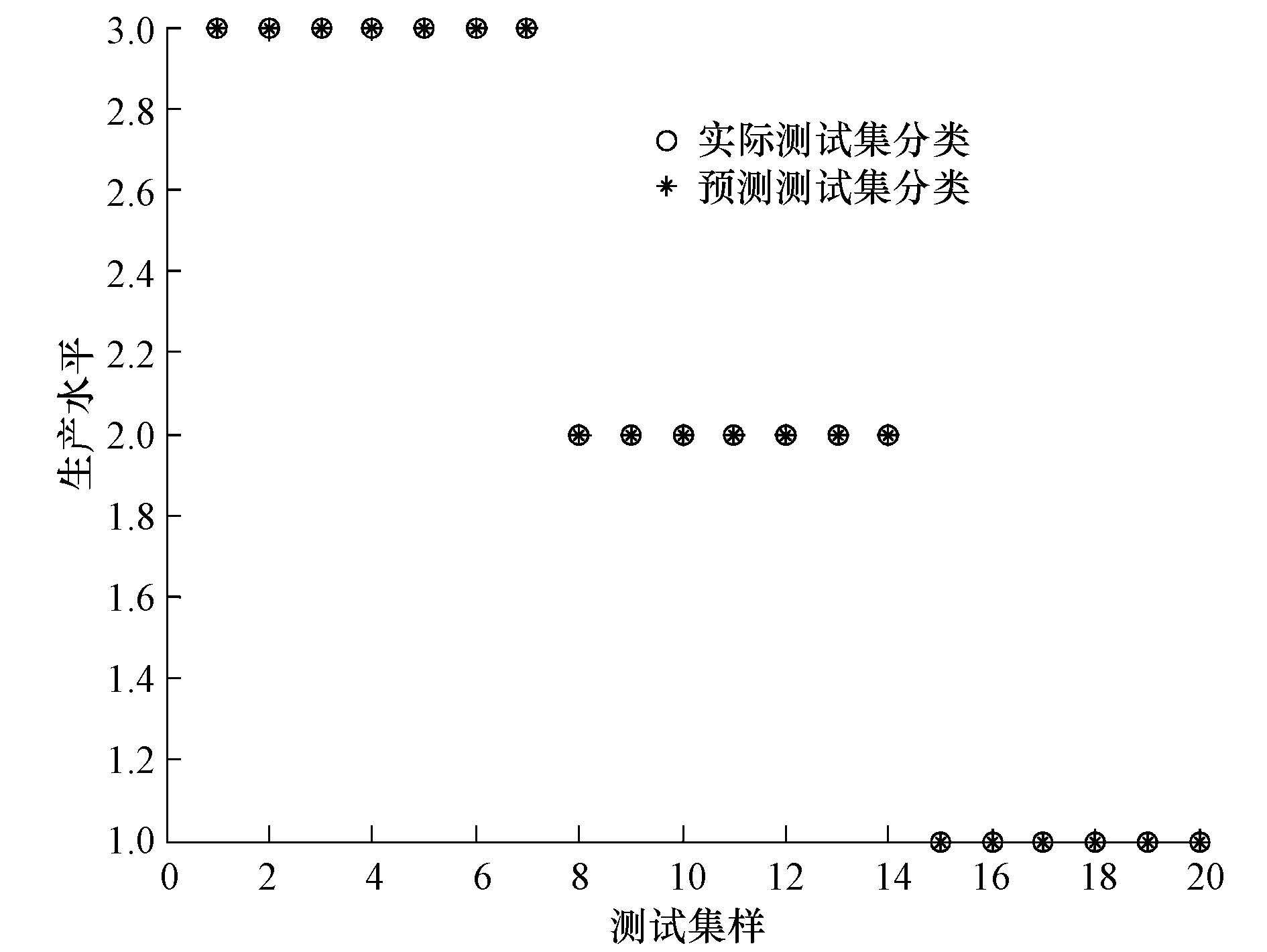图6 GA-SVM的测试集实际分类和预测分类对比 Fig.6 Comparison between actual classification and prediction classification of GA-SVM test set

为验证评价模型的优越性，本研究基于所建立的指标体系，分别选取3种不同工艺类型的3家具有代表性的企业进行现场数据采集(共9家企业)，不同工艺类型的评价标准不同，其中，第1、6、7家企业采用的是水浸工艺，第2、5、8家企业采用的是弱酸浸工艺，第3、4、9家企业采用的是直接酸浸工艺.将改进后的GA-SVM评价方法分别与传统评价方 法、机器学习方法进行比较.传统学习方法选取目前在清洁生产时间评价过程中应用较多的单因子评价法和AHP-Fuzzy方法，机器学习方法选择BP神经网络评价法和网络搜索改进支持向量机方法(GS-SVM).

由表 2可知，单因子法得出的清洁生产水平结果相对较低，企业整体清洁生产水平较差；AHP-Fuzzy方法在赋权计算中采用的是层次分析法，根据专家的经验和知识确定各指标因素的相对重要性，因此，具有较大的主观性和随机性，其中，企业5和企业7的评价结果与机器学习方法不一致，这是由于专家在对“一级综合利用指标”赋权较多，而以上两家企业的该项指标参数较高，因此，评价结果不一致；BP神经网络法对企业6的评价结果与其它4种方法存在差异，该企业的二级指标中各项有关循环利用的指标均为0，生产技术特征指标中总回收率仅为55%，明显与一般生产水平要求不符，说明基于梯度下降法的BP神经网络出现了“欠学习”现象，对于有限的小样本(30个)训练集，能对现有的生产工艺状况充分的模拟却不能充分的学习，从而导致其可推广能力较差，这就说明BP神经网络在小样本训练条件下建立的评价模型其泛化能力有较明显的下降；GS-SVM评价结果与GA-SVM完全一致，但由于GS是根据参数集C设为步长为1的指数反向增长：{C=29，28，…，21，20}，d按步长l正向增长：{d=l，2，…，10}，进行搜索，从检测时间来看，GS的判定速度较慢，说明GA优化SVM参数对于本研究数据确实具有较好的分类效果，节约了操作时间.

表2(Table 2)

表2 企业现场采集数据及不同模型评价结果比较 Table 2 Comparison of different site data and assessment models results

表2 企业现场采集数据及不同模型评价结果比较 Table 2 Comparison of different site data and assessment models results 一级指标 二级指标 单位 各企业取值 企业1 企业2 企业3 企业4 企业5 企业6 企业7 企业8 企业9 资源与能源利用 单位产品综合能耗 t(标煤)· t-1 9.5 7.4 7.5 7 5.9 10 6.5 7.2 9.5 指标 单位产品新鲜水耗 m3 · t-1 390 140 175 160 120 410 310 140 180 单位产品物耗 t · t-1 16 0 30 20 16 52 17 17 35 生产技术特征指标 浸出率 70% 68% 80% 90% 73.5% 55% 75% 72% 70% 离子交换率/萃取率 98% 98% 98% 99% 99% 98% 98% 98% 沉钒率 98% 98% 98% 98.5% 99.5% 98% 99.5% 98% 98% 总回收率 70% 65% 77% 73% 78% 55% 70% 65% 67% 综合利用指标 离子交换/萃余废水循环利用率 50% 90% 100% 100% 100% 100% 80% 80% 沉钒废水循环利用率 50% 100% 100% 100% 100% 0 100% 80% 80% NH3综合利用率 80% 80% 80% 85% 95% 0 92% 80% 80% 焙烧炉窑排放气体综合利用率 70% 60% 70% 0 65% 70% 尾渣综合利用率 50% 50% 50% 70% 100% 50% 100% 50% 0 污染物产生指标 单位产品基准排水量 m3 40 25 19 17 19.6 310 18 22 20.7 单位产品基准排气量 m3 45000 41000 37890 30240 34000 52000 39000 37000 33450 SO2排放浓度 mg · Nm-3 420 290 264.5 890 287 270 颗粒物排放浓度 mg · Nm-3 110 90 100 120 100 100 HCl排放浓度 mg · Nm-3 90 0 42.6 1200 93 80 氨氮废水排放浓度 mg · L-1 55 40 55 52.47 35 8000 35 40 59 总钒废水排放浓度 mg · L-1 2.03 0.5 1.9 1.8 1.85 50 1.52 2.1 2.3 单位产品危险物产生量 t · t-1 0 0 0.01 0 0.01 0 0.01 0 0 环境经济指标 环保投资比例 10.2% 19% 12.5% 14.5% 21.2% 6.8% 13.1% 19.8% 11% 运行成本 元 · t-1 1000 2500 2000 2000 2300 600 2000 2350 1500 尾矿渣资源利用效益 元 · t-1 20 40 45 65 60 20 60 40 0 生产工艺指标 生产规模符合国家政策要求 t 2000 1000 2000 2000 2000 700 2000 1000 1000 产品纯度 98% 99% 98.5% 99% 99.5% 96% 98.59% 98% 98% 尾渣堆放场的建设 基本符合 基本符合 基本符合 基本符合 基本符合 不符合 基本符合 不符合 不符合 执行环境保护法规 建设项目环境影响评价制度执行情况 部分执行 部分执行 部分执行 部分执行 部分执行 部分执行 部分执行 部分执行 部分执行 建立实施安全生产责任制度 部分执行 部分执行 部分执行 部分执行 部分执行 部分执行 部分执行 部分执行 部分执行 建立环境管理体系并通过认证 正在准备 正在准备 正在准备 已通过 已通过 未进行 正在准备 正在准备 正在准备 评价结果 单因子评价法 Ⅰ Ⅱ Ⅱ Ⅱ Ⅱ Ⅰ Ⅱ Ⅰ Ⅰ AHP-Fuzzy Ⅱ Ⅱ Ⅱ Ⅲ Ⅲ Ⅰ Ⅲ Ⅱ Ⅰ BP神经网络 Ⅱ Ⅱ Ⅱ Ⅲ Ⅲ Ⅱ Ⅱ Ⅱ Ⅰ GS-SVM Ⅱ Ⅱ Ⅲ Ⅲ Ⅲ Ⅰ Ⅱ Ⅱ Ⅰ GA-SVM Ⅱ Ⅱ Ⅲ Ⅲ Ⅲ Ⅰ Ⅱ Ⅱ Ⅰ 注：Ⅰ：淘汰水平；Ⅱ：一般水平；Ⅲ：清洁生产水平.

1)基于已建立的石煤提钒清洁生产评价指标体系，利用GA解决SVM的核函数及参数选择，建立了GA-SVM清洁生产评价方法，通过训练样本在对各类核函数进行结果对比后确定RBF函数为核函数，各类工艺最终确定的参数分别为强酸浸工艺C=2.1049，g=5.2184；弱酸浸工艺C=0.0035286，g=1.9947；水浸工艺C=0.39587，g=1.4105.将上述参数带入GA-SVM模型，通过20组测试样本，发现最终评价结果与实际工艺水平相符，预测测试精度达到100%.

2)通过与其他评价方法对比表明，在研究有限样本问题时，训练好的GA-SVM方法针对小样本数据在分类精度和可操作性上都较其他方法有明显优势，应用于石煤提钒行业清洁生产评价领域中，不仅可以解决评价指标多而存在的完整数据不足的问题，还可降低采集数据的评价成本，是一种具有较高实用价值的小样本评价方法，拓展了SVM应用范围，进一步丰富了清洁生产评价方法.