通过数学模型对污水处理的生化过程进行模拟分析一直是污水处理运行与管理领域的研究热点.20 世纪 50 年代以来，国外一些学者把反映生化过程机理的微生物生长动力学引入污水处理领域(顾夏声，1993；Lawrence et al., 1971；Henze et al., 1987).20世纪 80年代末，国际水协会(IWA)提出的活性污泥 1号模型(ASM1，Activated Sludge Model No. 1)取得了很大的成功，是早期较为完善的污水处理数学模型研究之一(Brdjanovic et al., 2000; Salem et al., 2002; Rodriguez Roda et al., 2002; Thesen et al., 1974).通过模拟计算，使污水处理的设计和运行更加理论化和系统化，提高了人们对污水生物处理过程的认识，不仅节省了大量的经济成本，而且提高了污水处理相关工作的质量和效率.

然而，随着污水处理工艺及设备设施的日渐复杂，活性污泥数学模型在污水处理厂的实际应用中具有一定的局限性.一方面，数学模型的建立过程比较复杂，需要对水质组分及动力学参数进行测定，大部分污水厂缺乏这方面的基础有效数据；另一方面，污水处理过程实际上是一个十分复杂的由物理、生物、化学等因素协同作用的过程，最终的处理效果不仅与决定其生物反应的一系列特征相关，同时还受大量不确定因素的影响，而活性污泥数学模型还远未将这些因素考虑在内，这在一定程度上降低了模型预测的精确性和实际应用价值(韦安磊，2010).

对此，笔者提出可通过基于数据驱动的黑箱模型对污水厂处理效果进行模拟预测.然而污水处理过程中去除污染物的种类很多，每种类型污染物都有其独特的去除机理和影响因素，因此，仅通过建立一个黑箱模型就对所有指标进行预测势必无法保证准确性.综合考虑，本研究将黑箱模型主要用于污水处理脱氮工艺模拟分析，主要基于以下几方面原因：①污水厂出水总氮是评判其工艺水平和运行水平的重要指标之一，对于一般水厂而言要保持出水总氮平稳达标，存在一定的技术难度和较大的调控空间；②对于传统反硝化脱氮的机理及影响因素已研究的较为透彻，因此，可以很好地确定对脱氮效果有显著影响的参数，同时这些参数在一般污水厂都有大量的实际数据；③随着未来污水处理标准的日益提高，如何能保障前端脱氮效果，对后续深度处理工艺的成本控制有重要影响.

基于此，本文采用BP神经网络与马尔可夫链的组合预测模型，首先通过BP神经网络模型对北京某大型污水处理厂实际进出水数据和工艺参数进行粗略拟合；其次，利用马尔可夫链对拟合结果及误差进行状态划分以进一步提高预测精确度；最后，运用基于BP神经网络与马尔可夫链的组合模型预测分析该厂的实际出水水质.

神经网络模型是以神经元的数学模型为基础来描述的，是一种按误差逆向传播算法训练的多层前馈网络，它由网络拓扑、节点特点和学习规则来表示，能在未知被构建对象和输入参数的数学关系式的情况下，通过学习和贮存大量的输入-输出模式关系，自适应地获取输入与输出的非线性映射关系.这其中又属BP 神经网络的应用最为普遍，它使用最速下降法，通过反向传播来不断调整网络的权值和阈值，使网络的误差平方和最小.应用 BP 神经网络一般包括4个基本步骤：①确定网络结构形式；②收集训练和测试样本；③进行网络模型训练；④利用训练后的网络进行应用计算.

神经网络模型的模拟过程中会应用到大量的样本训练和测试数据，一般污水厂生产运行过程中会产生大量数据，但这些数据大部分是由人工或仪表检测而来，受取样、化验操作、瞬时波动、仪表等因素影响，这些数据经常存在误差和波动.用这样的数据进行神经网络的训练，往往会导致预测结果在一定范围内随机波动，降低了预测的准确性.马尔可夫链恰能有效地预见并消除由系统随机性而产生的预测误差.因此，通过建立神经网络与马尔可夫链的组合预测模型，将二者进行优势互补，能够得到更为准确的预测结论(王江荣等，2013)

马尔可夫链是根据俄国数学家马尔可夫发现的系统状态转移规律，分析随机事件未来发展趋势及可能结果的一种预测方法(孙克，2004)，其实质是对于事件发生的概率进行预测，根据目前状况来预测其将来时刻变动状况(夏乐天，2005).马尔可夫链预测主要分两个过程：一是确定马尔可夫链的状态空间；二是要通过计算确定状态转移概率与状态转移矩阵.

在事件发展变化过程中，状态E_i经过k步转移到状态E_j的转移概率P^k_ij为：

对于BP神经网络模拟预测的结果，通过马尔可夫链模型可以分析其误差的波动范围，并且预测波动的发展趋势，通过误差的状态转移概率矩阵对BP神经网络预测的结果进行进一步的精细优化.马尔可夫链是一个典型的无后效应随机过程，即模型在时刻t的状态只与它的前一个时刻t-1的状态条件相关，与以前的状态条件独立.

在污水处理过程中，下一时刻污染物浓度变化情况只与当前时期(8~12 h)的系统状态有关，而与之前的状态无关.此外，该模型的最终预测结果不是一个具体数值，而是生成一组不同概率的预测区间值，该方法可从一定程度上弥补因化验产生的数值误差，提高预测准确度.

本文采用北京某大型污水处理厂的实际生产数据为实验依据，该厂设计日处理规模100万m³ · d^-1，其主体工艺采用A/O法去除有机污染物(COD)和总氮(TN)，同时还通过投加化学药剂来去除总磷(TP)，最终出水主要指标可稳定达到《城镇水污染物排放标准》(GB18918)中的一级B标准.

由于污水处理过程中每种类型污染物的去除都有其各自的原理和特点，因此，其影响因素也各不相同.例如，对于BOD、COD等有机指标，一般水厂均能较彻底的去除，其出水的残留值主要与原水中的溶解性不可降解有机物有关.再例如悬浮物指标，主要与沉淀单元的水力负荷和状态点有关，而与其它水质指标关联不大，等等.其中，总氮是污水中的主要污染物之一，其去除机理和影响因素目前研究的较为明确，因此，本文主要以脱氮工艺模拟为研究对象，对该厂出水总氮进行数学模拟分析.

以该厂2013年全年数据为基础，共收集了365组样本集，其中250组作为训练集，115组作为测试集.试验工具采用新西兰怀卡托大学开发的WEKA数据挖掘应用平台，BP神经网络输入层节点数为 8，分别表示进水流量、生物反应池温度、进水BOD、进水COD、进水TN浓度、进水NH⁺₄-N浓度、生物反应池MLSS浓度、生物反应池MLVSS浓度；输出层节点为出水TN浓度，隐藏层数取1，迭代次数为500，采用不同的隐含层节点数分别对网络进行训练，当隐含层节点数取4时，神经网络训练误差最低(平均误差0.073).利用训练后的模型，以2013年各月的月均参数值为输入量(表 1)，模拟各月月均TN值，模拟结果与真实值的线性相关度为0.921(图 1).

表1(Table 1)

表1 北京某污水处理厂2013年1—12月主要运行数据 Table 1 Operational data from a WWTP in Beijing in 2013

表1 北京某污水处理厂2013年1—12月主要运行数据 Table 1 Operational data from a WWTP in Beijing in 2013 月份 进水量/ 104m3 T/℃ BODin/ (mg · L-1) CODin/ (mg · L-1) TNin/ (mg · L-1) NH+4-Nin/ (mg · L-1) MLSS/ (mg · L-1) MLVSS/ (mg · L-1) TNout/ (mg · L-1) 1 1303 14.8 182 408 49.8 39.4 4996 2757 27.1 2 1124 14.9 178 421 49.6 39.1 4965 2427 28.0 3 1279 15.7 172 428 49.7 39.3 5365 2776 29.0 4 1268 17.1 176 419 52.0 41.0 5134 2785 27.1 5 1267 21.0 212 468 52.7 41.3 4814 2383 26.7 6 1343 23.0 220 486 49.3 37.5 4578 2070 26.2 7 1614 24.9 170 410 12.0 32.6 4046 2109 25.1 8 1587 25.2 158 385 45.8 34.8 3293 2041 23.5 9 1495 24.7 172 385 45.7 35.3 3179 2041 25.2 10 1498 24.2 193 430 51.7 39.9 3312 2219 27.9 11 1395 20.4 170 369 55.1 43.4 3556 2503 29.5 12 1452 17.2 191 417 54.0 43.2 4132 3236 29.8

图1(Fig.1)

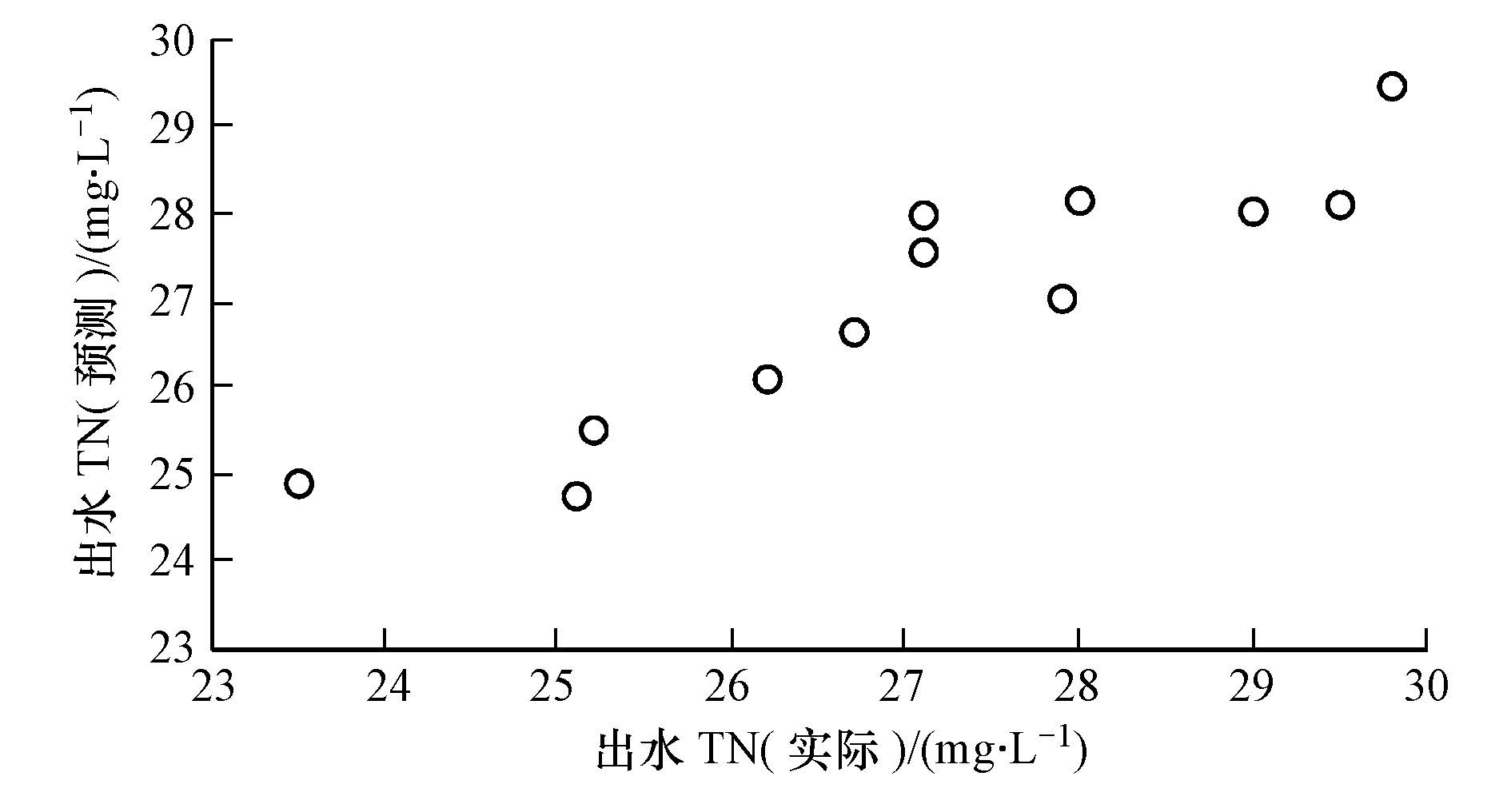图1 神经网络模型拟合结果 Fig.1 Curve Fitting with a neural network model

利用训练后的神经网络对该厂2014年1—12月数据进行模拟预测，最终模拟值与实际值对比情况如图 2和表 2所示.从表 2可以看出，12个月的数据模拟误差范围为±10%，有3次模拟结果低于实际值，9次高于实际值.其中，最小误差为0.79%，最大误差为9.49%.

表2(Table 2)

表2 污水处理厂实际出水水质及BP网络计算拟合值 Table 2 The real and predicted value of effluent TN

表2 污水处理厂实际出水水质及BP网络计算拟合值 Table 2 The real and predicted value of effluent TN 月份 TNout/ (mg · L-1) BP拟合值/ (mg · L-1) 绝对误差/ (mg · L-1) 相对误差 1 28.8 30.1 -1.31 -4.54% 2 30.2 28.1 2.09 6.91% 3 28.5 29.8 -1.37 -4.81% 4 28.8 28.2 0.57 1.99% 5 25.9 27.6 -1.70 -6.55% 6 26.1 26.7 -0.64 -2.45% 7 25.5 25.3 0.20 0.79% 8 25.5 26.1 -0.58 -2.28% 9 24.5 26.8 -2.33 -9.49% 10 26.3 27.5 -1.21 -4.60% 11 27.1 27.4 -0.35 -1.31% 12 27.3 28.2 -0.97 -3.56%

图2(Fig.2)

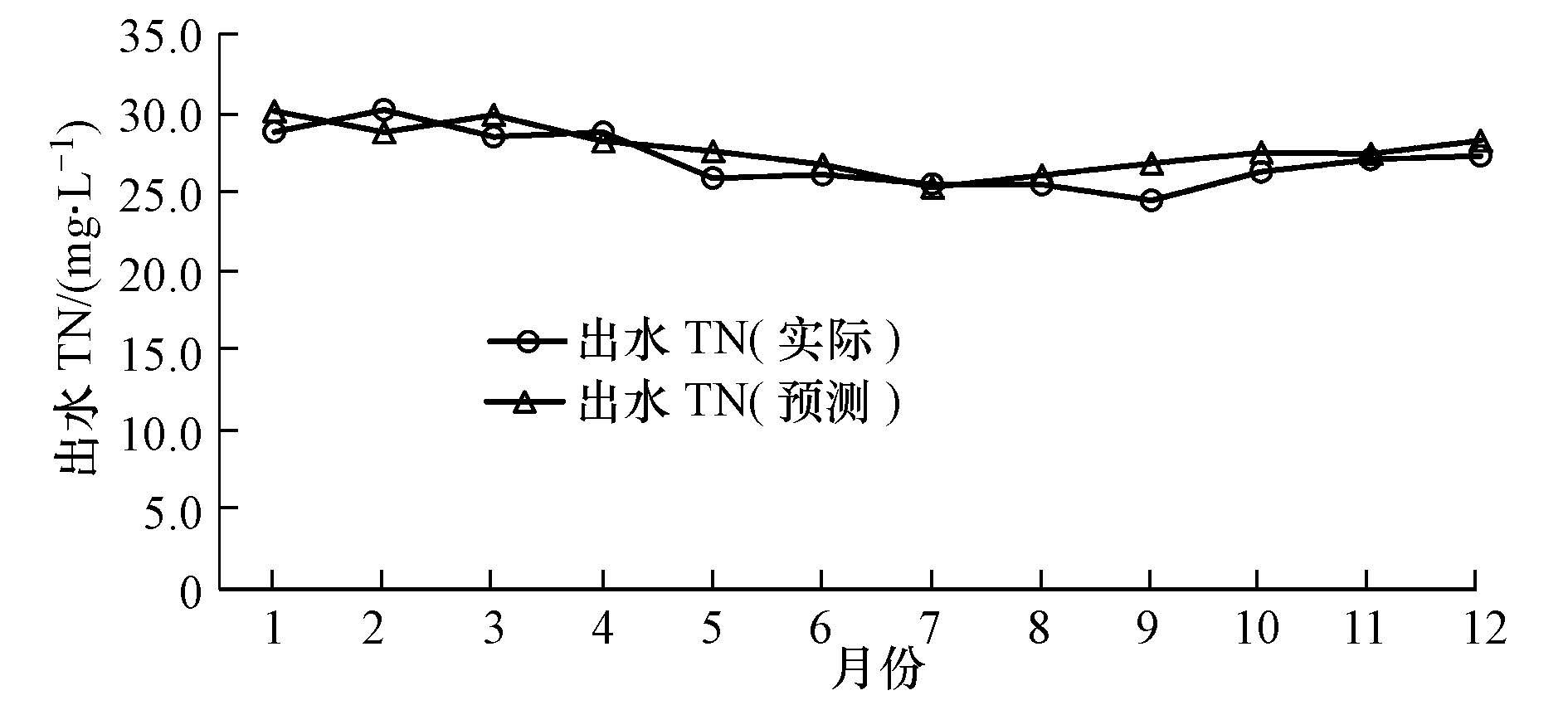图2 出水TN实际值与拟合值对比 Fig.2 The Real and predicted values of effluent TN

马尔可夫链的预测精度主要由转移矩阵决定，为了构造转移矩阵，首先需要合理划分误差状态区间，一般以样本-均方差方法来确定.以样本的均值 为中心，标准差s=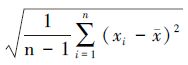为标准进行分组.一般可将数据序列分为：(x-s，x-0.5s)、(x-0.5s，x+0.5s)、(x+0.5s，x+s)等几组.

从表 2可以看出，模拟值与实际值误差在-10%~5%之间，误差平均值为x=-2.5，标准差为s=4.28.根据均值-标准差分级方法，通过BP模拟结果的误差均值和标准差，可将马尔可夫状态区域划分为4种状态：a[-10%，-5%]，b[-5%，0]，c[0，+5%]，d[5%，10%]

对于马尔可夫链，描述其概率性质的重要的量是转移概率矩阵.把转移概率P_ij=(n，n+k)记为P_ij，当k=1时，P_ij(1)称为1步转移概率，记为P_ij.设 P 表示一步转移概率P_ij(k)所组成的矩阵(式(2))，且状态空间E={1，2，…，n}，则 P 称为系统状态的一步转移概率矩阵.

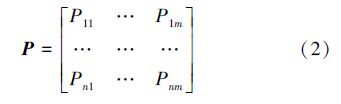
根据之前的3种区域状态划分，p_ij为由状态i转向状态j的频数，如p_ab表示当前误差在a状态，下一组模拟误差在b状态的频数，其余以此类推.设：

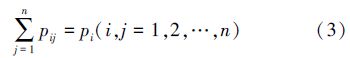
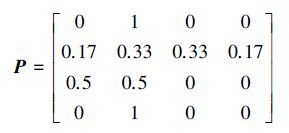
那么由状态i转向状态j的转移概率为f_ij≈p_ij/p_i，(i=1，2，…，n)，这样便可得到BP模拟出水TN误差的一步转移概率矩阵，具体如表 3和式(3)所示.

表3(Table 3)

表3 污水处理厂出水水质预测结果的马尔可夫状态转移表 Table 3 Markov state transition for the BP forecasted results of the estate effluent data

表3 污水处理厂出水水质预测结果的马尔可夫状态转移表 Table 3 Markov state transition for the BP forecasted results of the estate effluent data 状态 a b c d 合计 a 0 2 0 0 2 b 1 2 2 1 6 c 1 1 0 0 2 d 0 1 0 0 1 合计 2 6 2 1 11

检验随机过程是否具有马氏性是应用马尔科夫链模型的必要前提，通常离散序列的马尔科夫链是用χ² 统计量来检验的.

_j表示(n_ij)_q×q的第j列之和同各行各列的总和的比值，P_ij表示状态i转到状态j的概率，计算公式如下：

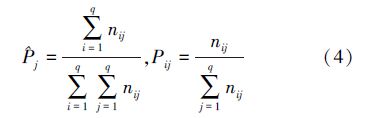
统计量服从自由度为(q-1)²的χ²分布.选定置信度α，查表得χ²_α((q－1))²，令：

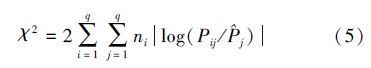
若χ²>χ²_α((q－1))²，则{r_i，i=T}具有马氏性.对该厂12个月的状态序列做马氏检验.根据表 3再结合步长为1的一步转移概率矩阵 P，可算得统计量χ²=32.14，给定置信度α=0.05，查表可得分为点χ²_a(4)=27.85.由于χ²>χ²_α((q－1))²，故这组序列满足马氏性.

根据2014年1—12月模拟结果，通过马尔可夫链预测模型，得到2015年1—5月出水总氮状态转移表，结果如表 4所示.其中，参考2014年12月的模拟误差，初始向量为[0.17，0.33，0.33，0.17].

表4(Table 4)

表4 2015年1—5月出水TN预测状态向量 Table 4 The forecasting state vectors of TN from January to May in 2015

表4 2015年1—5月出水TN预测状态向量 Table 4 The forecasting state vectors of TN from January to May in 2015 状态 出水TN预测状态向量 1月 2月 3月 4月 5月 a 0.17 0.22 0.16 0.19 0.18 b 0.33 0.61 0.54 0.54 0.55 c 0.33 0.11 0.20 0.18 0.18 d 0.17 0.06 0.10 0.09 0.09

综上，得出2015年1—5月出水的最终预测结果(表 5).马尔可夫链改进后的预测结果是不通过概率下的区间范围值，符合污水厂出水水质和检测结果在一定程度呈随机变化的特性，通过最大概率区间预测值可以很准确地预测实际出水水质范围.从该厂2015年1—5月的模拟预测结果可知，出水的实际水质均符合最大概率区间内的预测范围值，表明基于 BP神经网络与马尔可夫链的组合预测模型具有较高的精度，可应用于污水处理的水质模拟.

表5(Table 5)

表5 污水处理厂2015年1—5月出水实际值、BP拟合值与马尔可夫改进值对比情况 Table 5 Real data，fitting value by BP， and value improved by using Markov chain of the effluent TN from January to May in 2015

表5 污水处理厂2015年1—5月出水实际值、BP拟合值与马尔可夫改进值对比情况 Table 5 Real data，fitting value by BP， and value improved by using Markov chain of the effluent TN from January to May in 2015 月份 实际值/(mg · L-1) BP拟合值/(mg · L-1) 改进后预测结果/(mg · L-1) 概率 [28.14，29.48] 0.17 1 26.8 27.1 [26.8，28.14] 0.33 [25.89，26.8] 0.33 [24.09，25.89] 0.17 [30.13，31.57] 0.22 2 28.7 30.1 [28.7，30.14] 0.61 [27.72，28.7] 0.11 [25.8，27.72] 0.06 [29.71，31.13] 0.16 3 28.3 28.5 [28.3，29.72] 0.54 [27.34，28.3] 0.2 [25.44，27.34] 0.1 [31.29，32.78] 0.19 4 29.8 31.1 [29.8，31.29] 0.54 [28.79，29.8] 0.18 [26.79，28.79] 0.09 [33.07，34.65] 0.18 5 31.5 32.9 [31.5，33.08] 0.55 [30.43，31.5] 0.18 [28.32，30.43] 0.09

1)污水处理过程是多种复杂生物化学反应综合作用的结果.本文所采用的模拟方法和预测模型是对传统污水处理数学模型的一种补充，即通过数据挖掘手段，采用基于BP 神经网络与马尔可夫链的组合预测模型，充分挖掘出数据中的变化规律与拟合趋势，恰好弥补了传统数学模型的不足.

2)通过对北京某污水处理厂实际数据分析计算表明，BP神经网络模型结合马尔可夫链组合模型具有很好的适用性，能够准确预测出水水质范围.在不掌握生物反应机理模型参数或缺乏数据的情况下，为污水处理厂水质模拟提供了一种新的途径.

3)本方法尤其适合于运行工艺和进出水水质相对稳定，且具有大量历史数据积累的水厂.由于污水处理过程影响因素的多样性和不确定性，对于不同类型的水厂，在具体建模时还应结合实际情况，在神经网络输入层节点(即污水处理的影响因素)选取和马尔可夫状态区域划分方面进一步研究分析.