真光层深度定义为水柱中支持净初级生产力的部分,其底部为临界深度,即水柱的日净初级生产力为零值时的深度(韩博平等,2001).在海洋、湖泊、河流等水生生态系统中浮游植物基本上都分布在这一层,且浮游植物初级生产力、生物量的垂向分布一般均以真光层深度为下界,该深度有时也被称为光合层厚度.真光层深度研究除在湖泊初级生产力和营养盐估算方面有意义之外,还有助于进行湖泊生态修复和水质改善.张运林等认为沉水植物修复的可行途径为物理消浪恢复岸边水生植物和湖滨湿地带,借助水生植物抑制底泥再悬浮,提高真光层深度,甚至在水下光照严重不足时,可以采用水下光补偿系统技术为沉水植物生长提供光源(张运林等,2006).可见真光层深度对水生生态环境演变及修复有着重要意义.
真光层深度一方面取决于水体中各类物质对光的衰减,另一方面还与到达水表面的光强和光场入射角度(邱辉等,2011)有关.对真光层深度的定义不尽相同,其中之一是依据水下光强14 μmol · m-2 · s-1 对应的深度称为真光层深度(Reinart et al., 2001);大多数研究为方便起见,采用表面光强衰减到1%或1/e的深度来代替真光层深度.水体中介质的散射与吸收作用是造成光随深度衰减的成因,不同水体介质组成对其衰减特性也不甚相同.总悬浮物是最主要的散射体,主要包括无机悬浮物和有机悬浮物,不同总悬浮物组成成分不同,是导致其散射特性存在差异的原因之一.太湖水体的总悬浮物主要是由无机悬浮物构成的,很多学者也对其散射特性以及主导因子进行了研究,如孙德勇等(2007)建立了太湖水体总悬浮物浓度与散射之间的关系模型,并对影响总悬浮物散射的主导因子进行分析,认为无机悬浮物主导着总悬浮物的散射;在可见光波段范围内各水体要素对总吸收系数的贡献大小顺序是:浮游植物>非藻类颗粒物>CDOM(孙德勇等,2008).太湖悬浮物中主要以无机颗粒为主,但有机物的比例也不小,达30%(张运林等,2004).无机悬浮物主要是碎屑矿物、粘土矿物等,有机悬浮物则包括浮游植物、浮游动物残体等同时也囊括了活体浮游植物及存在于活体浮游植物的叶绿素;除悬浮物外,有色可溶性有机物也是水体介质的一部分,同样对辐射具有吸收作用.有研究认为,真光层深度主要受制于4种物质,即纯水、有色可溶性有机物、非藻类颗粒物及浮游植物(Kirk,1994);也有研究进一步分析得到,真光层深度主要受悬浮物浓度影响,其次则是叶绿素a浓度,溶解性物质对其影响甚微(Bricaud et al., 1988).总之,水体中不同介质的组成和浓度差异是造成真光深度空间分异的关键因素.
以往对光合有效辐射真光层深度的研究是基于所有波段整体而言的,而400~700 nm辐射中蓝光的衰减最强,绿光和红光的衰减最弱,且浮游植物在蓝光440 nm以及红光670 nm附近为其特征吸收,因而单纯的由光合有效辐射总量得到的真光层深度还不能完全反应浮游植物在光合层的分布(张运林等,2006).逐波段真光层深度影响因子的研究显得更加有意义,藻类等浮游植物对整个光合有效辐射的吸收具有较大的波段性差异,因而定量确定不同波段处各影响因子的贡献量,有利于针对具体波段处真光层深度的确定与研究,更好地为光补偿技术提供理论依据.张运林曾分析了太湖单个站点的真光层深度谱分布(张运林等,2006),但太湖真光层深度谱的空间分异及其影响因素的研究仍然相对缺乏.因而针对真光层深度谱的空间分异及其影响的研究有助于水生生态系统的治理和修复.
鉴于本文采样时段为5月,紫外辐射造成的黄质降解较大(赵巧华和秦伯强,2008a),其吸收贡献也相应较弱,因而本文忽略黄质的影响作用.本文拟利用实测辐射数据得到全湖28个站点真光层深度光谱分布曲线,并对其进行谱型分析;随之进行谱型聚类,对比分析与验证(按照已有经验知识)谱型与介质浓度组成间的关系;最后逐波段定量分析无机悬浮物浓度,有机悬浮物浓度以及叶绿素a浓度对真光层深度值的贡献.
2 数据与方法(Data and methods)本文采用于2010年4月29日—5月2日,对28个采样点进行采样并测量得到的数据.其中光谱数据使用剖面测量法分层测量水表至水下1.2 m处,每隔10 cm共13层的水体下行辐照度,测量仪器为德国Trios生产的RAMSES水下光谱仪;由于太湖为大型浅水湖泊,其风浪作用显著,水体光学性质相对较为均一,因而采集于水体上层50 cm水样带回实验室测定光学介质等参数.有机悬浮物、无机悬浮物浓度数据采用重量法(GB /T 11901—1989)测定,叶绿素a浓度则采用热乙醇法测定(张丽彬等,2008).辐射数据与浓度数据的测定时间一一对应,且采样均在基本相似的风浪条件下进行.
2.1 采样点分布采样点随机分布于全湖,编号并记录下经纬度,如下图 1所示.1~6号点以及32号点位于蓝藻频发的典型藻型湖区梅梁湾,16、17号点位于藻型湖区竺山湾,13、14以及31号点位于草、藻型交接地带贡湖湾,24~30号点以及12号点位于草型湖区胥口湾与东太湖,其余位于湖心区.
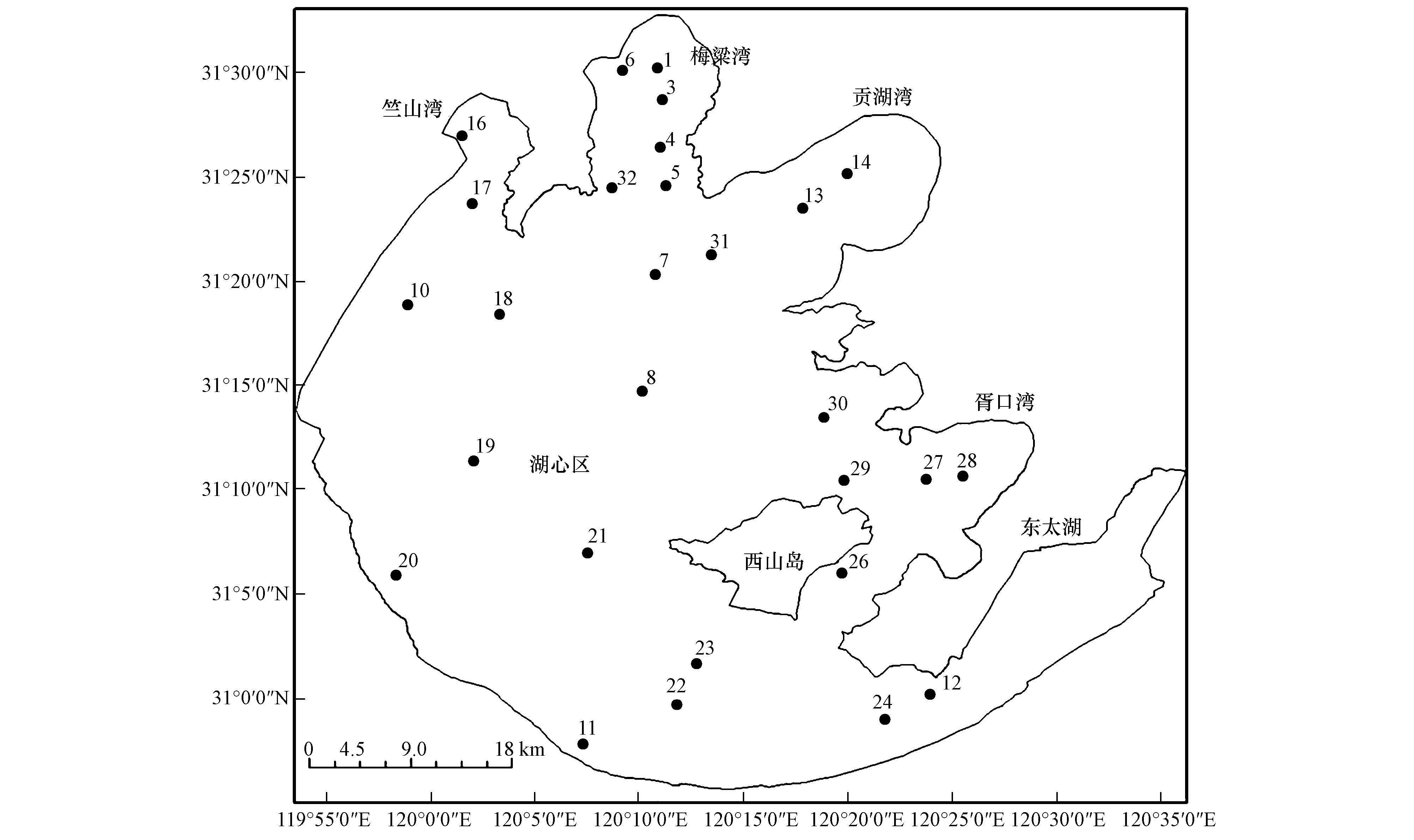 |
| 图1 采样点分布图 Fig.1 Distribution of sampling stations |
本文研究的光合辐射是根据采样点的剖面测量计算得到.将辐照度为水表面辐照度1%处的深度视为真光层深度,其与光衰减系数存在一定量关系,可以表示为:
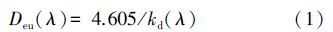
漫射衰减系数按式(2)进行计算(Kirk,1994)
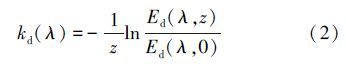
为利于谱型研究,本文借鉴Bricaud提出的平均吸收系数,构建标准化真光层深度谱,去除振幅对谱型的影响(Bricaud et al., 1988),式子如下:
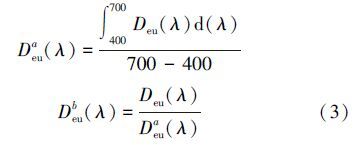
逐波段对真光层深度Deu(λ)与无机悬浮物浓度xISS、有机悬浮物浓度xLOI、叶绿素a浓度xchl-a数据进行岭回归分析,构建逐波段真光层深度影响因素的回归模型.
由于本文所研究的自变量间存在共线性,使得一般的逐步回归分析方程不稳定,或者隐藏自变量对因变量影响显著性,甚至出现回归系数的正负与实际不符(高惠璇,2000).本文改用岭回归分析,运用岭迹图法确定使得各回归系数趋于稳定的岭回归参数k,得到更加稳定的回归系数(曾繁会和吕渭济,2001),建立Deu(λ)与各介质浓度因子的回归方程,参数k的定义及具体确定方法参见该文献.
此外,对所有站点真光层深度谱分布曲线,利用Ascending Hierarchical对曲线的向量空间余弦相似度(cosine)运用最小方差法(ward)进行聚类,结合水体介质浓度分析谱型特征差异.
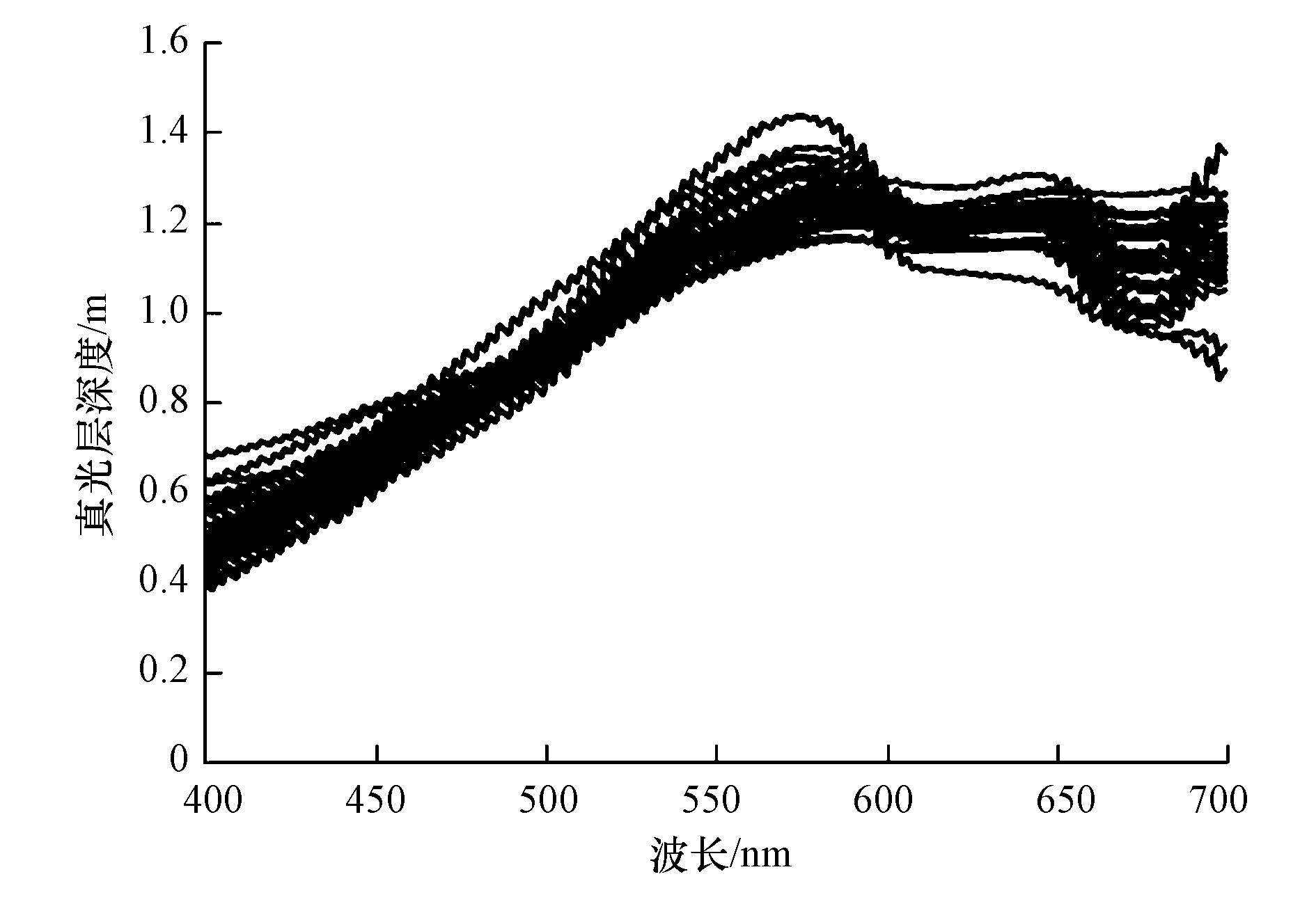
3 结果与分析(Result and analysis) 3.1 标准化真光层深度谱由图 2可见,各采样点的真光层深度谱分布曲线总体较为相似,在575 nm左右处具有峰值,650 nm处具有肩峰,605与675 nm处具有谷值.
 |
| 图2 标准化真光层深度波谱分布图 Fig.2 Stand arded spectral distribution of euphotic depth |
已有研究表明,太湖总悬浮物的散射光谱特征为近似水平直线,仅在675 nm附近出现较平缓谷值(施坤等,2010),太湖有机悬浮物的光谱吸收特征则为440 nm处具有峰值,550 nm处降到小值,620 nm处有一凸起,650 nm处小值开始上升达到675 nm处的吸收峰.而无机悬浮颗粒物的光谱吸收特征为随波长增加按指函数递减(张运林等,2005),且在550 nm左右处降到小值.而总悬浮物的光谱吸收综合了二者的特征,按其有机与无机组分不同比例呈现出3种特征(孙德勇等,2008),此种特征也即下文谱型聚类特征的基础.由此,结合总悬浮物的光谱散射与吸收光谱特征,此处其叠加效果即为对辐射的衰减,3种介质对真光层深度波段谱在575 nm处的波峰均有明显贡献,而有机悬浮物则对650 nm处以及675 nm处的波谷具有明显贡献.
此外,叶绿素a明显的吸收光谱特征为436 nm与675 nm处具有峰值,540 nm左右处有吸收谷,在650 nm左右开始上升(赵巧华等,2008b).然而由于400~500 nm左右总悬浮物的吸收明显大于叶绿素a的吸收,因而其在436 nm处的吸收峰表现在对真光层深度变化谱的贡献上就被弱化了,从图 2中看出,436 nm处无明显特征,而540 nm处叶绿素a吸收谷应有处的真光层深度高值与575 nm高值合并为一个大波峰.650 nm处吸收值的增加对应此处真光层深度谱的减小.因而叶绿素a对标准化真光层谱650 nm以及675 nm处的波峰有明显贡献.
而600~650 nm处谱型由575 nm处的峰值下降并保持平值,原因可能为此处无机悬浮物的吸收几乎不再减少,且有机悬浮物与叶绿素a吸收均在该范围内(620 nm左右)有所增加(加上太湖优势藻种蓝藻具有的藻兰素在620 nm处的吸收峰作用),结合下文得到的三者在该范围的贡献度,得出三者对谱型的影响效果近为平直.
综上,该谱形575 nm处的大波峰由3种介质共同作用决定;600~650 nm间的过渡区域、650 nm处以及675 nm处的波谷主要是由有机悬浮物与叶绿素a吸收特征共同作用的结果.
3.2 聚类分析考虑到上文分析结果,及太湖悬浮物浓度普遍较大的特征,在400~500 nm波段范围内,无机悬浮物浓度对真光层深度影响较大且弱化了有机悬浮物与叶绿素a的影响,该波段无机悬浮物的影响将起绝对主导作用,对该波段聚类没有明显效果;而500~600 nm范围内,无机悬浮物对真光层深度谱型影响也具有显著作用,因此500~600 nm波段范围单独聚类;而600~700 nm范围则为有机悬浮物与叶绿素a主导作用,因此对600~700 nm进行单独聚类.
为便于分析,聚类结果选为两类,得到空间分布见图 3.图 3a中两类曲线特征不明显,该波段聚类空间分布也较分散无明显空间分布特征,整个湖区在该波段的特点近乎一致,无机悬浮物多寡几乎都动摇不了其决定性作用,符合该波段范围内真光层深度主要由无机悬浮物决定这一结论.而图 3b中两种类型的分布也较为分散,3种介质共同作用时,大部分聚为一类,只有梅梁湾与贡湖湾处4个点以及湖心区处一个站点为第二类,且这两类特征差别不明显.
 |
| 图3 谱型聚类空间分布及曲线特征图(a、b、c分别表示400~500 nm、500~600 nm及600~700 nm波段谱型聚类分析图) Fig.3 Spatial patterns of the clustered spectral distribution and the characteristics |
对于图 3c,竺山湾、梅梁湾、贡湖湾以东太湖口的12号站点分为一类,其余为第二类.结合图两类曲线特征来分析,可得类型1曲线走势在该波段范围内呈下降趋势,且650与675 nm处的波峰与波谷较第二类明显,类型2在该波段范围内较平缓650与675 nm处特征不明显.结合站点介质浓度数据分析,发现类型1对应介质浓度中,有机悬浮物与叶绿素a相对含量较高,且主要是有机悬浮物相对较高,表现为有机悬浮物及叶绿素a与总悬浮物浓度比值均较类型2大.
由上文分析得到的结论中,标准化真光层深度谱575 nm处的峰值主要由3种介质共同决定,605 nm、675 nm处的波谷以及650 nm处的波峰均由有机悬浮物与叶绿素a的吸收特性作用形成.因而当LOI与chl-a含量大的时候这几处的峰谷特点更明显,该处结论与上文分析相吻合.
此外,600~700 nm聚类结果也具有实际意义,竺山湾与梅梁湾为典型的藻型湖区,贡湖湾为藻草型交接地带,这些区域藻类等浮游植物生长旺盛,有机悬浮物浓度大,藻类色素包括叶绿素a浓度同样高,尽管梅梁湾、贡湖湾、河口区等无机悬浮物浓度也较高,但是相比湖心区有机悬浮物浓度相对较低而言,这些区域的有机悬浮物与无机悬浮物浓度比值较大(叶绿素a类似).太湖作为大型浅水湖泊,底泥再悬浮导致悬浮物浓度较高,特别是湖心区,无机悬浮物浓度更是比各湖湾高,因而第二类草型湖区与大太湖,特征为无机悬浮物浓度占相对优势.此外,12号点处于东太湖湖口区域,位于太湖东南部的一个狭长湖湾,受风浪的作用小,且该处水生植物对水体起着过滤、净化、消浪、抑制底泥上浮的作用(张运林等,2004),因此无机悬浮物浓度很低,使得绝对浓度较小的有机悬浮物和叶绿素a具有较高的相对浓度,具有与类型一相似的真光层深度光谱分布曲线形状.
3.3 真光层深度与ISS、LOI、Chl-a岭回归分析在水体中光的衰减主要取决于悬浮物颗粒物浓度和溶解性物质浓度,而根据PAR衰减系数主要受悬浮物浓度决定,其次是叶绿素a浓度,溶解性物质的影响甚微,其仅为0.0012,未通过显著性检验(张运林等,2006).本文将悬浮物分为有机悬浮物和无机悬浮物,分别分析其对真光层深度的影响.同时进一步研究叶绿素a浓度对各波段真光层深度的影响情况.欲逐波段对每个采样点真光层深度与对应站点有机悬浮物浓度、无机悬浮物、叶绿素a浓度进行线型回归分析.
鉴于14、16号站点叶绿素a浓度偏离回归线较大,回归分析前将其剔除,因而回归分析样本数为26,经分析,3个自变量之间具有明显的共线性,见表 1.自变量间的共线性使传统的逐步回归分析出现回归系数反常以及重要变量被剔除模型等现象,因而无法使用逐步回归建立较准确的模型(高惠璇,2000).
| 表1 真光层深度影响因子变量相关表 Table 1 Variable correlation and confidence level |
表 1显示3个变量间的相关性,LOI与ISS具有较强相关性.因而结合已有真光层深度影响因素的研究结论,利用岭回归分析上述3个变量与真光层深度的线性回归系数,构建线型模型:
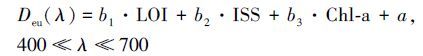
Deu(λ)为λ波段处的真光层深度(m),b1、b2、b3分别为LOI、ISS、Chl-a的系数(LOI、ISS、Chl-a均为标准化浓度数据),a为常数项.
由于与总悬浮物浓度和叶绿素a浓度的线性回归显著性均很高(张运林等,2006),同时把有机、无机悬浮物浓度以及叶绿素a浓度3个变量均放入模型中,使用岭回归分析法进行处理.使岭迹趋于稳定,得到显著性较高的回归系数,p值均小于0.005.
真光层深度与3个变量之间的回归系数波段分布图如图 4所示.此处的贡献是指3种介质对于真光层深度值的绝对贡献.由a,b两图可知,ISS、LOI、Chl-a三者系数均为负,ISS系数绝对值即负贡献(下文简称贡献)最大,LOI其次,Chl-a最小;LOI与Chl-a的贡献分布趋势一致,在470 nm(Chl-a在440 nm)左右与675 nm左右处有峰值;而ISS则相反,675 nm处其对真光层深度的影响有谷值,400 nm处最大,逐渐减小至500 nm左右处.
 |
| 图4 5月份LOI、ISS、Chl-a回归系数(a)及贡献率(b)的波段分布图 Fig.4 Spectral distribution of the regression coefficient(a) and contribution rate(b)of variables LOI、ISS、Chl-a |
530 nm之前,Chl-a贡献率在0.04~0.08之间,ISS在0.49~0.58之间,LOI在0.37~0.45之间,加之ISS在该波段的辐射吸收及散射大于LOI,因此该波段范围内的光谱分布曲线形状贡献与值的贡献均主要为ISS.而后的波段范围内,LOI贡献率有所增加而ISS稍有减小,虽然Chl-a贡献率较530 nm之前更小,但ISS吸收及散射曲线平坦,此时LOI与Chl-a的吸收特征便凸显出来,尤其是675 nm处二者对值贡献的明显增加,也使得其对光谱分布曲线形状影响更明显.
4 讨论与结论(Discussion and conclusions) 4.1 讨论真光层是浮游植物进行光合作用产生有机物的场所,层内生物生产力被视为是支持其它生物过程的基础(张运林等,2006).太湖湖心区平均真光层深度仅为1~1.2 m,且在400 nm的蓝光波段出现最小值以及675 nm的红光处具有明显谷值,因而对于光合作用所需的蓝紫光与红光范围,其真光层深度尤其小于整个PAR真光层深度.处于较深处的浮游植物以及沉水植物,由于无法获得足够光合作用所需光能而面临衰竭,真光层深度远远小于水深也是造成许多浅水湖泊沉水植物消退的主要原因之一(Gulati and van Donk,2002),在本文无机悬浮物对真光层深度负贡献占50%以上以及有机悬浮物占近50%的基础上,认为通过物理消浪工程降低底泥再悬浮,是提高真光层深度进而促进水生植物尤其是沉水植物的一个有效途径,此外甚至可以采用定量水下光补偿技术,针对性地对有效波段范围进行光补偿,促进沉水植物向浅层湖表扩展.有望形成一个沉水植物生长-抑制沉积物悬浮-提高水体透明度-进一步促进沉水植物生长的良性循环(张运林等,2006).
4.2 结论1)真光层深度光谱分布特性在575 nm处的波峰主要由3种介质共同作用决定;600~650 nm间的波谷、650 nm处的波峰以及675 nm处的波谷主要由LOI与Chl-a吸收特性共同影响作用形成.
2)600~700 nm聚类结果具有明显的生态意义,无机悬浮物浓度的相对含量决定真光层深度波段分布的谱形.本次聚类将藻型湖区竺山湾、梅梁湾与藻草型交接地带贡湖湾分为一类,该类的谱形特征为675 nm处波谷明显,水体介质含量特点为有机悬浮物与无机悬浮物浓度比值较大(叶绿素a类似);而草型湖区与大太湖分为一类,此类型675 nm处波谷不甚明显,为无机悬浮物主导型.
3)岭回归能较好的模拟与ISS、LOI、Chl-a之间的线性关系,克服逐步回归中出现的变量间共线性问题,得到更合理的回归系数,将逐波段真光层深度的因素影响定量化,675 nm处回归模型为:

| [1] | Bricaud A, Bédhomme A L, Morel A. 1988. Optical properties of diverse phytoplanktonic species:experimental results and theoretical interpretation[J]. Journal of Plankton Research, 10(5):851-873 |
| [2] | 高惠璇. 2000. 处理多元线性回归中自变量共线性的几种方法——SAS/STAT软件(6.12)中REG等过程增强功能的使用[J]. 数理统计与管理, 20(5):49-55 |
| [3] | Gulati R D, van Donk E. 2002. Lakes in the Netherlands, their origin, eutrophication and restoration:state-of-the-art review[J]. Hydrobiologia, 478(1/3):73-106 |
| [4] | 韩博平, 韩志国, 付翔. 2001. 藻类光合作用机理与模型[M]. 北京:科学出版社 |
| [5] | Kirk J T O. 1994. Light and Photosynthesis in Aquatic Ecosystem (2nd ed)[M]. Cambridge, Britain:Cambridge University Press. 47-144 |
| [6] | 邱辉, 赵巧华, 孙德勇, 等. 2011. 太阳高度角对太湖水体真光层深度变化的影响分析[J]. 中国环境科学, 31(10):1690-1696 |
| [7] | Reinart A, Arst H, Erm A, et al. 2001. Optical and biological properties of Lake Vlemiste, a water reservoir of the city of Tallinn II:Light climate in Lake Vlemiste[J]. Lakes & Reservoirs:Research & Management, 6(1):75-84 |
| [8] | 施坤, 李云梅, 朱利, 等. 2010. 滇池水体总悬浮物散射系数参数化模型[J]. 环境科学学报, 30(7):1479-1485 |
| [9] | 孙德勇, 李云梅, 乐成峰, 等. 2007. 太湖水体散射特性及其与悬浮物浓度关系模型[J]. 环境科学, 28(12):2688-1694 |
| [10] | 孙德勇, 李云梅, 黄家柱, 等. 2008. 太湖梅梁湾夏季水体组分光谱吸收特性[J]. 生态学报, 28(2):749-760 |
| [11] | 曾繁会, 吕渭济. 2001. 基于MATLAB的岭回归分析程序设计及其应用[J]. 辽宁工程技术大学学报(自然科学版), 20(6):838-839 |
| [12] | 张丽彬, 王启山, 徐新惠, 等. 2008. 乙醇法测定浮游植物叶绿素a含量的讨论[J]. 中国环境监测, 24(6):9-10 |
| [13] | 张运林, 秦伯强, 陈伟民, 等. 2004. 太湖水体中悬浮物研究[J]. 长江流域资源与环境, 13(3):266-271 |
| [14] | 张运林, 秦伯强, 陈伟民. 2005. 梅梁湾藻华暴发期颗粒物和有色可溶性有机物的吸收光谱[A]//第十五届全国遥感技术学术交流会论文摘要集[C]. 贵阳:中国地理学会. 38 |
| [15] | 张运林, 秦伯强, 胡维平, 等. 2006. 太湖典型湖区真光层深度的时空变化及其生态意义[J]. 地球科学 D辑:地球科学, 36(3):287-296 |
| [16] | 赵巧华, 秦伯强. 2008a. 太湖水体介质吸收有效光合辐射能量的谱特征及其季节变化[J]. 环境科学学报, 28(9):1813-1822 |
| [17] | 赵巧华, 秦伯强. 2008b. 藻类的光谱吸收特征及其混合藻吸收系数的分离[J]. 环境科学学报, 28(2):313-318 |
 2016, Vol. 36
2016, Vol. 36


