2. 国立东京工业大学大学院综合理工学研究科环境理工学创造专攻, 东京 226-8503 日本
2. Department of Environmental Science and Technology, Interdisciplinary Graduate School of Science and Engineering, Tokyo Institute of Technology, Tokyo 226-8503, Japan
感潮河段是河流和海洋的交汇地带,受到河流淡水径流和海洋潮流共同作用,盐-淡水在河口段混合,从而导致海水侵入到感潮河段.近年来,河口水体缺氧的现象时有发生,且呈逐年恶化的趋势(Brown et al., 2011; Li et al., 2014).溶解氧是河口水质的重要指标,缺氧状态会严重影响水生生态系统的平衡(Kuo et al., 1991).当水体中的溶解氧浓度小于2 mg · L-1时,水生生态系统中的各种微生物、动植物就会受到严重的影响(Kim et al., 2010).在感潮河口上游,通常还会建有河口堰,更进一步加剧了河口生态环境的恶化.感潮河段缺氧现象的影响因素比较复杂,一般认为是河流径流、海洋潮流及水闸调度综合作用的结果.因此,对感潮河段复杂的水动力学及其伴随的物质输运过程进行系统研究,可以明确感潮河段水体发生缺氧的机理,为河口生态环境的进一步改善提供科学依据.
感潮河段的水流范围较大,流动情况复杂,受时间、空间及采样频率的限制,现场数据采集和精确测试变得非常困难.此外,影响河口形成缺氧水体的因素较多,河口的溶解氧浓度变化的时间尺度较小,甚至短于1天,所以很难仅仅通过实地观测来明确缺氧水体的动态特征及形成机理(Nezlin et al., 2009).采用数值模拟计算可以综合考虑多种因素的影响和捕捉短时间内溶解氧的变化规律,是在实地观测基础上研究感潮河段水动力学和物质输送规律的有力手段.尤其是随着计算科学的最新发展及数值模拟手段的不断突破,越来越多的学者都开始重视应用数值模拟来研究感潮河段的环境流体力学问题(Falconer et al., 1997; Borsuk et al., 2001; Ji et al., 2007; Kim et al., 2010).近几年来,研究者深入研究并建立了水流的三维模型,具有代表性的模型有美国普林斯顿大学的基于POM模式改进的ECOM模型,以及荷兰的Delft模型和美国麻省大学的FVCOM模型.利用这些模型进行网格划分时,在水深方向上一般采用σ坐标系,可有效地处理变化显著的复杂地形.这虽然在一定程度上弥补了以往z坐标系无法有效拟合地形的缺点(Cheng,1976),但σ变换会在水深变化剧烈的区域带来严重的数值计算误差.同时,采用σ坐标系时,为了降低盐-淡水分界面处的数值扩散误差,一般需要增加水深方向上网格层数,这会在浅水区域造成所谓的“过度解析”(over-resolution),增加了计算负担(Wang et al., 2008).因此,对感潮河段的水流进行数值模拟计算时,需要进一步完善计算域的网格划分,以便减小盐-淡水分界面处的数值扩散误差,从而提高计算精度.
基于此,本文提出一种算盘式自适应网格系统离散计算域,构建了三维水动力学和物质输送模型,综合考虑径流、潮流和水闸调度对水流流动及物质输送过程的影响.通过对典型感潮河段的盐度和溶解氧浓度的分布进行数值模拟,并与现场观测数据进行比较,证实计算模型的可靠性.同时,本文也分析感潮河段缺氧水体的时空分布规律,并讨论盐度分层密度、盐水在感潮河段停留时间及水闸调度对缺氧水体形成和发展的影响.
2 水动力学和溶解氧输送模型(Hydrodynamic and dissolved oxygen transport model) 2.1 算盘式网格系统采用算盘式网格系统剖分计算域(图 1).算盘式网格系统是基于中国传统算盘结构的一种网格划分方法,由格子面、格子线和格子点组成自适应网格结构.格子线平行地布置在格子面上,而格子点像算盘珠子一样可以自由地在格子线上移动.格子线上的格子点可以根据密度梯度在水深方向上的分布规律移动,保证在密度变化大的区域,进行局部密布格子点.
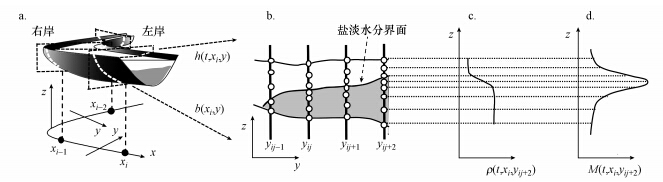 |
| 图 1 算盘式网格系统示意图 Fig. 1 Schematic view of Soroban grid system |
如图 1a、b所示,在设定的坐标系中,x轴沿河道最深线方向;y轴垂直于x轴,从右岸指向左岸;z轴是沿水深方向.算盘式网格系统分3步对计算域进行划分:①利用垂直于x轴的格子面离散计算域;②格子面采用平行的格子线进行离散化处理;③格子点布置在格子线上,这些格子点可以在格子线上自由移动,保证在密度梯度大的区域密布格子点.
在图 1b中,格子点布置在格子线上,每一条格子线上的格子点在每个时间步长都要进行重新布置以便跟踪自由水面和盐-淡水分界面的变化.为了能够在盐-淡水分界面附近密布格子点,需要应用下面的监控函数M找到盐-淡水分界面的位置.
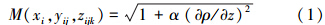
式中,xi、yij、zijk是格子面i格子线j上的格子点k的位置(m);α是比例系数(正数);ρ是t时刻(xi,yij,zijk)位置处流体的密度(kg · m-3).
在图 1c、d中,在格子面i上的格子线j+2上,密度在盐-淡水分界面附近发生阶跃,监控函数M的数值在分界面处相对较大,根据水深方向上监控函数的大小关系,就能捕捉到分界面的位置(Nakamura et al., 2010).为了确定每一个格子点在下一个时刻的新位置,需要将M的分布曲线沿水深方向积分,然后将积分值均分为若干部分,每一个部分的边界对应一个格子点的新位置.
根据上述方法,既能保证格子系统在每个时间步长后可跟踪自由水面的变化,同时也能在盐-淡水分界面附近加密布置格子点.
2.2 控制方程三维水动力学和溶解氧输送模型是基于三维的RANS方程、k-ε湍流闭合方程、自由水面迁移方程及盐度和溶解氧的输送方程,具体如下:
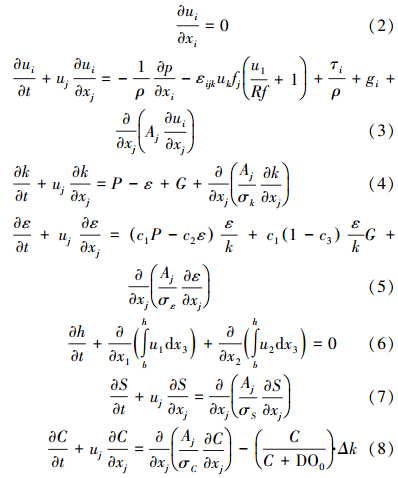
式中,t为时间(s);xi(x1,x2,x3)表示纵向、横向和水深方向的空间坐标(m);ui(u1,u2,u3)代表各坐标方向上的速度分量(m · s-1);p为压力(Pa);εijk为置换符号;ρ为水体密度(kg · m-3),根据温度在20 ℃下水中的盐度值来确定(UNESCO,1981);gi(0,0,g)是重力加速度(m · s-2);τi(τ1,τ2,τ3)是自由水面、河床底面和侧岸各坐标方向上总的剪切应力(N · m-2);R是河道的曲率半径(m);fj(0,0,f)为科氏力系数;k是湍动能(m2 · s-2);ε是湍动能耗散率(m2 · s-3);P是由于速度在水深方向上的梯度造成的湍动能生成项(m2 · s-3);G是由于浮力作用造成的湍动能耗散项(m2 · s-3);Aj(A1,A2,A3)表示各坐标方向上的动量扩散系数(m2 · s-1);S表示盐度(psu);C表示溶解氧的溶度(mg · L-1);DO0表示溶解氧半饱和常数(mg · L-1);Δk是氧消耗速率(mg · L-1 · d-1);h为自由水面高度(m);b为河床底面高度(m).k-ε的模式常数c1=1.44,c2=1.92,c3=1.0,cμ=0.09,σk=1.0,σε=1.3,σs=0.8,σc=1.0.
2.3 数值求解基于时间分裂法(time-splitting)(Yabe et al., 2001; Yabe et al., 2004; Nakamura et al., 2006),将控制方程组依据物理过程分割成一系列的中间步骤,分别进行数值求解.同时,为了完成上述控制方程的求解,还需要在自由水面和河床底面设置合理的边界条件.水流在自由水面的动力学边界条件及在河床底面的运动学边界条件分别为:
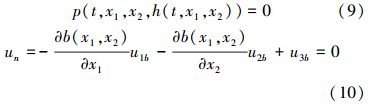
式中,un为河床底面法向速度(m · s-1);u1b、u2b、u3b为河床底面处的速度在各方向的分量(m · s-1).
盐度输送方程在自由水面和河床底面的边界条件为:

溶解氧输送方程在自由水面和河床底面的边界条件为:
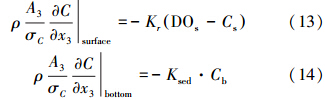
式中,Kr为曝气系数(m · s-1);DOs为自由水面处饱和溶解氧溶度(mg · L-1);Cs为自由水面处溶解氧的实际浓度(mg · L-1);Ksed为河床底面单位面积上的脱氧系数(mg · m-2 · d-1);Cb为河床底面处溶解氧的实际浓度(mg · L-1).
以上介绍的三维模型适用于模拟计算多尺度具有自由水面的不可压缩密度分层大型水体的水动力学和物质输运过程.离散计算域时提出采用算盘式的网格系统,相对于传统的z坐标系和σ坐标系,可以在不增加计算负担的基础上有效降低数值扩散误差.此外,模型采用并行计算技术,极大提高了处理速度,初步测试表明,20 CPU计算速度是单CPU计算速度的9.8倍.
3 研究对象和模型参数设置(Study object and model parameter setting) 3.1 研究对象以某感潮河段为例,其平面图如图 2所示.图中KP(Kilometer Position)表示沿河道最深线(x轴)距离入海口一定距离的某处位置(如2 KP表示距入海口2 km).感潮河口的河道大体上是直的而没有大的蛇形弯曲部分.枯水时河道宽约600 m,洪水时河道的宽度会扩大到1000 m.在距离入海口18.5 km的上游修建了河口堰,主要目的是用于防止盐水的上溯.河口堰的水闸调度是根据上游的观测站(距入海口76.5 km)的流量及河口堰上下游的水位差和盐度值来调配的.在洪水时感潮河口堰的水闸会全部开放;而在枯水时则保持全部关闭或部分闸门、部分开放的状态.
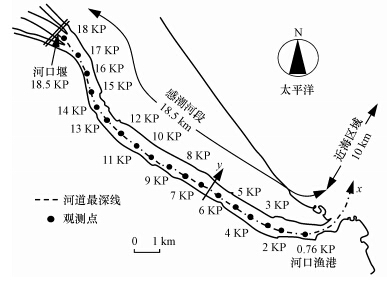 |
| 图 2 感潮河口平面图 Fig. 2 Plan view of tidal estuary |
利用三维水动力学和溶解氧输送模型模拟计算1997年8月1日—31日间该感潮河段盐度和溶解氧的分布规律.在此期间内,铃木等(Suzuki et al., 2003)每周利用多项目水质计(ACL-1183-PDK)乘船从2 KP至18 KP(图 2)每隔1 km选取观测点测定了盐度和溶解氧沿水深方向的分布.观测点是在河道横截面水深最深的地方.在一个观测点,多项目水质计从水面缓慢放下,每隔0.1 m记录盐度和溶解氧值,在每个观测点平均耗时2.5 min,然后乘船移动到下一个观测点实施观测.计算区域选取自感潮河河口堰至离岸10 km的区域,合计为28.5 km(图 2).模型的网格分辨率在纵断面方向上选取感潮河段Δx1 = 100 m,近海区域Δx1=200 m;在横断面方向上Δx2= 25 m;在水深方向上初始时刻为Δx3=0.1 m.
上游速度的边界条件由感潮河河口堰的放流量及水闸调度来确定.下游处速度的边界条件由河口渔港(0.76 KP)实测的潮位来确定.图 3给出的是8月该感潮河河口堰的放流量及渔港处实测的潮位的变化情况.盐度和溶解氧在上游的边界条件由水闸调度确定,在闸门开放的位置S=0 psu,C=9 mg · L-1;而在闸门关闭的位置∂S/∂x=0,∂C/∂x=0.盐度和溶解氧在下游的边界条件是S=34 psu,C=9 mg · L-1.模拟计算始于1997年7月22日,以便消除初始条件对计算结果的影响.初始速度场为静止场;盐度、溶解氧和水位的初始值则是根据7月22日的观测数据给定.此外,与该感潮河河口溶解氧输送过程相关的参数设置为Kr=3.0×10-5 m · s-1,Ksed = 0.17 mg · m-2 · d-1,DO0= 0.5 mg · L-1,Δk= 0.6 mg · L-1 · d-1(Suzuki et al., 2003).
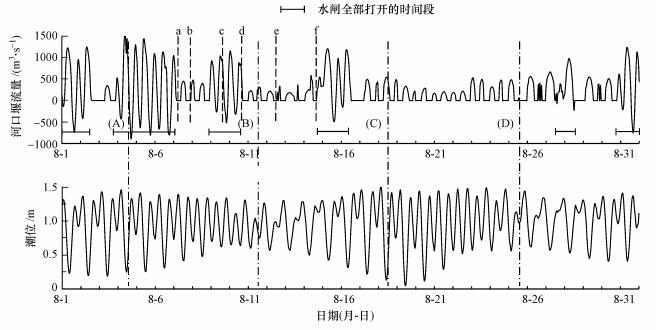 |
| 图 3 1997年8月感潮河放流量和河口渔港实测潮位 Fig. 3 Freshwater discharge from the tidal river and tidal level at harbor in August,1997 |
图 4比较了盐度沿河道最深线分布的观测结果和计算结果,黑色表示河床面.观测时间对应图 3中点划线A~D,8月4日和8月18日是大潮,8月11日和8月25日是小潮.图 5给出了大潮至小潮不同日期正午时刻盐度沿河道最深线分布变化的模拟结果.从图 4的观测结果可以看出,由于大潮时潮流的能量高导致感潮河段湍流强度大,感潮河段盐淡水混合程度相对小潮时剧烈,盐度成层变弱;而在小潮时潮流能量低,盐淡水混合被削弱,高盐度的海水一直上溯到河口堰附近,感潮河段形成稳定的盐度成层.图 5的模拟结果很好地证实了从8月18日(大潮)至8月25(小潮)间随着潮流能量的减弱,高盐度海水不断上溯形成稳定盐度成层这一现象.图 6给出了不同的观测日选取的6个观测点处水深方向盐度分布的模拟结果和观测值的对比.8月4、11、18和25日盐度模拟结果和观测值的最大误差分别为9.37、14.9、10.3和11.6 psu.虽然个别水深处模拟结果与观测值相差较大,但水深方向的盐度分布很好地再现了感潮河段的分层特征.此外,由于入海口处河道相对狭窄(图 2),速度剪切对湍流的强化作用要大于密度分层对湍流的抑制作用,导致此处沿水深方向盐度分布相对比较均匀.盐度的计算结果和观测值总体吻合较好,较好地再现了盐-淡水的时空分布规律,表明构建的三维水动力学模型能够用来模拟该感潮河河口密度流的动态特征.
 |
| 图 4 盐度沿河道最深线纵向分布的观测结果和模拟结果的比较(a.观测结果;b.模拟结果) Fig. 4 Comparisons of longitudinal profiles of measured and simulated salinity along the deepest line(a. measured data; b.simulated results) |
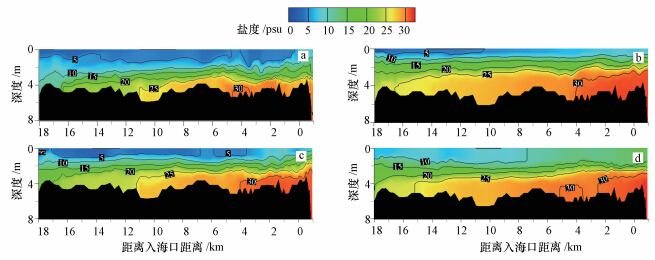 |
| 图 5 大-小潮间盐度沿河道最深线纵向分布的模拟结果(a. 8月8日,b. 8月20日,c. 8月22日,d. 8月25日) Fig. 5 Longitudinal profiles of simulated salinity along the deepest line during spring-neap tide |
 |
| 图 6 不同日期选择的观测点处水深方向盐度分布的观测值和模拟值比较 Fig. 6 Comparisons of measured and simulated vertical salinity profiles at selected locations in different days |
以上的结果讨论表明,在这个感潮河段,潮汐能量及地形的作用对盐水和淡水的混合产生了很大影响.较强的潮汐涨落和狭窄的河道都以增加速度剪切强化湍流混合的形式造成密度分层界面波动,使盐-淡水间发生掺混,从而使感潮河段的盐度分层强度减弱.
4.2 溶解氧的分布图 7给出了溶解氧沿河道最深线分布的观测结果和模拟结果的比较,黑色表示河床面.从观测结果可以看出,在8月4日,河口堰附近就出现了低溶解氧的水体,而明显大范围地在盐水楔的前端出现缺氧水体则发生在8月11日(小潮时).再过1周后,到了8月18日(大潮时),盐水楔前端的缺氧水体由于河口环流的作用沿着盐-淡水分界面逐渐向下游扩展,缺氧水体的范围进一步扩大.在8月25日(小潮时),水体缺氧状态不断恶化,感潮河段接近一半的区域形成了缺氧水体,尤以盐水楔最前端溶解氧的溶度为最低.溶解氧输送模型的模拟结果合理地再现了溶解氧在盐水楔内的变化规律,可知在密度分层河口缺氧水体易于在盐水楔前端形成,在河口环流的作用下,缺氧水体会不断向下游输送.
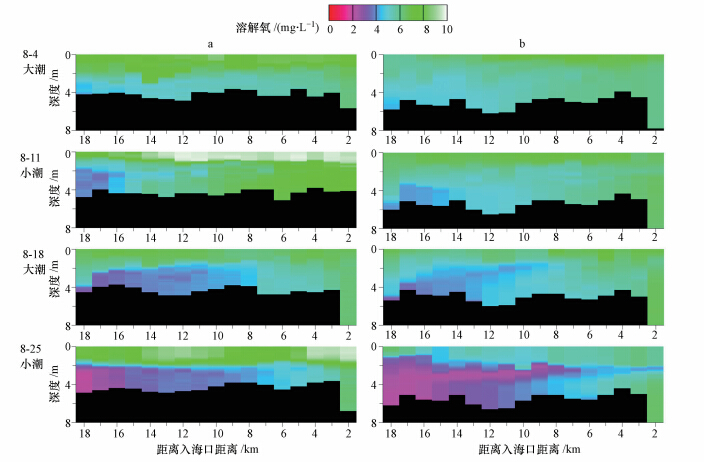 |
| 图 7 溶解氧浓度沿河道最深线纵向分布的观测结果和模拟结果的比较(a.观测结果;b.模拟结果) Fig. 7 Longitudinal profiles of measured and simulated DO concentration along the deepest line(a. measured data; b.simulated results) |
以上的结果讨论表明,在这个感潮河段,缺氧水体易于在盐水楔的前端形成,随大-小潮的周期性变化缺氧水体的面积和程度也发生相应的变化.缺氧水体的空间位置与盐水层基本契合,表现出垂向分布层化特征,表层的溶解氧浓度要高于底层.
4.3 缺氧水体形成的影响因素 4.3.1 盐度成层强度的影响从图 4和图 7可以看出,盐度成层强度对缺氧水体的形成起到了促进作用.8月4日大潮时,河口堰径流流量较大,流量峰值达到1500 m3 · s-1.径流一方面将感潮河段高浓度的盐水冲刷到下游,使盐水层变薄;另一方面强烈的湍流混合作用强化了盐-淡水层间的溶解氧交换,此时富含溶解氧的淡水层为盐水层补充了溶解氧.但随着径流和潮汐作用的减弱,高盐度的海水稳步上溯,逐渐形成稳定的盐-淡水分界面.密度分层强度的增加,抑制了上下层间的溶解氧交换,致使上部淡水层的溶解氧无法输送到下部盐水层.随着盐水层中溶解氧被底泥中有机物分解等因素的不断消耗,使溶解氧浓度不断下降,导致8月11日小潮时缺氧水体范围明显增大.至下一个小潮(8月25日)出现期间,虽然经历了一个大潮(8月18日)盐淡水层间相对较强的湍流混合作用,但盐度分层总体稳定,从而造成缺氧状态不断恶化,影响区域不断扩大.由此可见,感潮河段盐度成层强度与缺氧水体的形成和发展有着紧密的联系.
4.3.2 盐水停留时间的影响盐水在河口的停留时间可以用来判断来自海洋的富含溶解氧的“新水”与河口区域低溶解氧的“旧水”交换频率的大小,从而判断来自海洋的溶解氧的供给与感潮河段缺氧水体的形成之间的联系.根据“释放染料”的方法,将下游边界处停留时间的边界条件设定为释放日期,就可以计算来自海洋的盐水在河口的停留时间.
图 8是来自海洋的盐水在感潮河段停留时间的模拟计算结果.图中的黑色表示河床面,蓝色表示盐水的停留时间.与图 5相对应,在8月4日盐水楔的前端首先出现了低溶解氧的水体(图 7).图 7与图 8对比发现,当来自海洋的盐水停留时间超过9 d时,盐水补充的溶解氧无法及时满足底泥和水体中有机物分解等因素造成的溶解氧的消耗量,因此,容易形成低溶解氧的水体.至8月11日,随着盐水停留时间的延长,缺氧水体在溶解氧前端的范围增大.盐水在感潮河段的停留时间在8月18日最长达到15 d,这直接导致了在盐水楔前端形成的缺氧水体范围继续扩大.到了8月25日,随着盐水停留时间的进一步延长,经过了18 d,缺氧水体从入海口扩大至河口堰附近.富含溶解氧的盐水在上溯过程中不断被消耗,在感潮河段停留时间越长,能向上游水体提供的溶解氧则越少,致使缺氧水体的范围进一步增大,且向入海口附近不断延伸.因此,盐水停留时间的计算结果表明,来自海洋的溶解氧供给率是影响缺氧水体形成和发展的另一个重要因素.
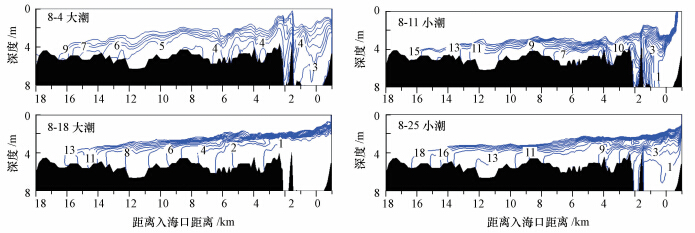 |
| 图 8 盐水的停留时间 Fig. 8 Residence time of seawater |
河口堰放流量的大小是由水闸调度来控制的.图 9给出了不同水闸调度条件下,河床处盐度和溶解氧时空分布的计算结果.图 9a~f对应的时间和河口堰放流量由图 3中虚线表示.a、d和e时刻水闸全部关闭,b和f时刻部分水闸打开放流,c时刻水闸全开放流.由图 9a可知,在经历了长时间水闸全开放流后,盐水楔的前端已经退却到11.5 KP附近,感潮河段河床处的溶解氧维持在7 mg · L-1左右.但随着部分水闸的关闭,放流量降低,盐水又重新上溯,河床处的溶解氧浓度逐渐下降(图 9b).到8月9日(图 9c),水闸全开放流在初始阶段仅仅对小范围的盐度和溶解氧分布产生了影响;而放流结束后(图 9d),底层的盐水再次被冲刷到感潮河段的中下部位置,河床处的溶解氧也恢复到较高的数值.到8月12日(图 9e),高浓度的盐水甚至上溯到河口堰附近,河床处的溶解氧浓度降低,部分区域出现了一定范围的缺氧水体.随着部分水闸关闭放流量减小,盐水楔趋于稳定,在感潮河段的中上部出现大范围的缺氧水体.因此,水闸调度决定了河口堰放流量的大小,直接影响来自径流溶解氧对感潮河段水体溶解氧的补给程度.
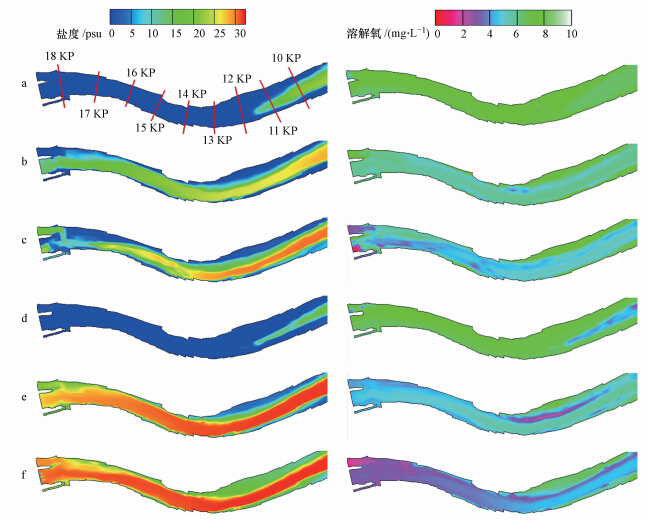 |
| 图 9 河床处盐度和溶解氧的时空分布的计算结果 Fig. 9 Simulated results of temporal and spatial variation of salinity and corresponding dissolved oxygen at the river bed |
1)考虑径流、潮流和水闸调度综合作用的三维数值模型可以很好地模拟计算感潮河段物质输运的时空分布规律.为了模拟感潮河段盐度、溶解氧等参数的动态过程,采用格子面、格子线和格子点组成的三维自适应网格结构,可实现格子点的局部加密,从而降低数值扩散误差.模拟结果与观测结果吻合较好,说明“算盘式网格结构”对精确求解感潮河段水动力学和溶解氧输送的三维数学模型是十分有效的.
2)感潮河段水体分层的强弱主要由潮汐的类型决定,潮流能量越高盐度分层越弱.感潮河段的缺氧水体首先出现在盐水楔的前端.随着时间的推移,缺氧状态会不断恶化,影响范围会向入海口不断扩展.在感潮河段,影响缺氧水体的形成和发展的主要因素有盐度分层强度、盐水在感潮河段的停留时间、河口堰水闸的调度情况.
| [1] | Borsuk M E, Stow C A, Luettich Jr R A, et al. 2001. Modelling oxygen dynamics in an intermittently stratified estuary: estimation of process rates using field data [J]. Estuarine, Coastal and Shelf Science, 52(1): 33-49 |
| [2] | Brown C A, Power J H. 2011. Historic and recent patterns of dissolved oxygen in the Yaquina Estuary (Oregon, USA): Importance of anthropogenic activities and oceanic conditions [J]. Estuarine, Coastal and Shelf Science, 92(3): 446-456 |
| [3] | Cheng R T. 1976. Numerical models of wind-driven circulation in lakes [J]. Applied Mathematical Modelling, 1(3): 141-159 |
| [4] | Falconer R A, Lin B. 1997. Three-dimensional modelling of water quality in the Humber Estuary [J]. Water Resource, 31(5): 1092-1102 |
| [5] | Ji Z G, Hu G D, Shen J, et al. 2007. Three-dimensional modeling of hydrodynamic processes in the St. Lucie Estuary [J]. Estuarine, Coastal and Shelf Science, 73(1/2): 188-200 |
| [6] | Kim T, Sheng Y P, Park K. 2010. Modeling water quality and hypoxia dynamics in Upper Charlotte Harbor, Florida, U.S.A. during 2000 [J]. Estuarine, Coastal and Shelf Science, 90(4): 250-263 |
| [7] | Kuo A Y, Park K, Moustafa M Z. 1991. Spatial and temporal variabilities of hypoxia in the Rappahannock River, Virginia [J]. Estuaries, 14(2): 113-121 |
| [8] | Li L, Ren J L, Yan Z, et al. 2014. Behavior of arsenic in the coastal area of the Changjiang (Yangtze River) Estuary: Influences of water mass mixing, the spring bloom and hypoxia [J]. Continental Shelf Research, 80: 67-78 |
| [9] | Nakamura T, Kojima T, Ishikawa T. 2006. CIP-Soroban method for two-dimensional estuary flow with a river width and free water surface [J]. Proceedings of Hydraulic Engineering, Japan Society of Civil Engineers, 50: 805-810 (in Japanese) |
| [10] | Nakamura T, Ishikawa T. 2010. A development of 3D CIP-Soroban solver for an estuary water flow [J]. Annual Journal of Hydraulic Engineering, 54: 1441-1446 (in Japanese) |
| [11] | Nezlin N P, Kamer K, Hyde J, et al. 2009. Dissolved oxygen dynamics in a eutrophic estuary, Upper Newport Bay, California [J]. Estuarine, Coastal and Shelf Science, 82(1): 139-151 |
| [12] | Suzuki T, Ishikawa T, Yokoyama K. 2003. Field measurement and numerical simulation of estuarine circulation in a river estuary [J]. Proceeding of River Engineering, 9: 259-264 |
| [13] | UNESCO. 1981. The practical salinity scale 1978 and the international equation of state of seawater 1980. UNESCO Technical Papers in Marine Science, 36: 25 |
| [14] | Wang Q, Danilov S, Schröter J. 2008. Comparison of overflow simulations on different vertical grids using the finite element ocean circulation model [J]. Ocean Modelling, 20(4): 313-335 |
| [15] | Yabe T, Xiao F, Utsumi T. 2001. The constrained interpolation profile method for multiphase analysis [J]. Journal of computational Physics, 169(2): 556-593 |
| [16] | Yabe T, Mizoe H, Takizawa K, et al. 2004. Higher-order schemes with CIP method and adaptive Soroban grid towards mesh-free scheme [J]. Journal of Computational Physics, 194(1): 57-77 |
 2015, Vol. 35
2015, Vol. 35


