根据水质监测历史数据，建立水质预测模型，准确地预测水体中污染物浓度随时间发展变化的趋势，是水环境管理和污染控制的基础工作.建立可靠的水质预测模型成为近年来水环境科学领域的研究热点之一.

水环境系统是一个受到生物、化学、物理、人为等多种因素影响的复杂系统，水质随时间非线性地变化，因此以传统方法很难建立一个精确的水质预测模型.然而，在一些局部水环境系统中，长期来看水质的变化是缓慢的、有规律可循的(Liu et al., 2013; Liu et al., 2014; 李冬等，2012).随着监测技术以及监测手段的多样化，通过对日益增多的监测数据进行分析和挖掘，借助近年来迅速发展的智能方法，建立人工神经网络非线性水质预测模型，使预测水体中污染物浓度随时间发展变化成为可能，并且已在水环境管理和污染控制中得到了应用(Maier and D and y， 2000).

目前，人工神经网络与支持向量机(Support Vector Machine，SVM)已广泛应用于金融、电力、医学及环境科学等领域的时间序列预测.在水质时间序列预测方面，人工神经网络预测模型(Durdu，2010; Gazzaz et al., 2012; 郭劲松等，2001; 李晓东等，2006; Maier and D and y， 1996，2000; Palani et al., 2008; Thoe et al., 2012)和SVM回归预测模型(Liu et al., 2013; Liu et al., 2014; Noori et al., 2012; Tan et al., 2012)也得到了一些较成功的应用.虽然人工神经网络具有强非线性映射和自适应能力，但其算法易出现过学习或欠学习、局部极小、网络结构难以确定、推广能力差等诸多问题(张成成等，2013).而SVM回归模型是一种建立在统计学习理论和结构风险最小化原则基础上的监督式学习方法(Vapnik，1995)，该方法通过引入核函数将原始输入映射到线性可分的高维特征空间，具有泛化能力强、不易发生过拟合等优点，能较好地解决小样本、非线性、高维数和局部极小点等问题(Liao et al., 2011; 毕温凯等，2012).与人工神经网络预测模型相比，SVM预测模型的性能有所提高(King et al., 2000; Singh and Gupta， 2012; Yuan et al., 2009).但在SVM预测模型中，核函数必须满足Mercer条件，支持向量的个数会随着训练样本的增加呈线性增加(De Martino et al., 2011).且只给出确定性的预测结果，没有概率输出，无法估计预测的不确定性(周建宝等，2013).而在实际应用中概率式的预测能够提供重要的信息，有助于确定水质预测的可信度.

关联向量机(Relevance Vector Machine，RVM)是Tipping于2001年在贝叶斯框架的基础上提出的一种较新的机器学习算法(Tipping，2001; Widodo and Yang， 2011)，其核函数不必满足Mercer条件，解的稀疏性也远高于SVM，且能够给出预测的概率信息，具有较好的泛化能力(孙斌和杨晓明，2012).RVM已在解决模式识别和回归估计等诸多实际问题中得到了应用，并取得了良好的效果(Samui and Dixon， 2012; 赵树延等，2011).因此，本文针对人工神经网络和SVM水质预测模型存在的问题，建立RVM水质预测模型，并以该模型对pH值、DO、COD_Mn和NH₃-N 4种重要水质指标进行预测.

RVM回归算法的详细原理可参见相关文献(Tipping，2001; Widodo and Yang， 2011).

将RVM用于水质预测，首先需依据监测的某一水质指标的历史数据时间序列建立RVM水质预测模型，然后以此模型预测该水质指标将来的变化.

设水质指标的历史数据时间序列为{y_n}_n=1^N，其中N为序列长度，y_n为n时刻的水质指标监测值，x_n=〖y_n-dτ，y_n-(d-1)τ，…，y_n-τ〗为之前的d个监测值组成的向量，τ是采样周期.则建立水质预测模型的关键在于确定映射关系：

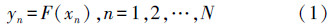
为此，需构建一训练样本集{x_n，y_n}_n=1^N，其中x_n为输入样本，y_n为输出样本，并以该样本集训练RVM，利用RVM回归极强的非线性映射能力，使RVM的输入与输出逼近式(1)，从而建立RVM水质预测模型.在此基础上，将后续水质指标的时间序列送入训练后的RVM预测模型输入端，即可在该预测模型输出端得到未来水质指标的预测值.

本文探讨pH值、DO、COD_Mn和NH₃-N这4种主要水质指标的预测.实验数据来源于中华人民共和国环境保护部网站(http://www.mep.gov.cn/)公布的全国主要流域重点断面四川攀枝花龙洞水质自动监测周报(2004年第1周至2012年第53周)，其中只有2011年的52周数据是完整的，其它年份均有1~6周不等的监测数据不全的情况，所以本应含469组的监测数据而实际上只有451组是完整的.水质预测属时间序列预测，任何一个时间点的数据缺失都会在一定程度上影响整体预测的准确性，故有必要将监测数据补全.本文选用Lagrange插值法将监测不全的数据补全.Lagrange插值法是一种多项式插值法，可以给出一个恰好穿过二维平面上若干个已知点的多项式函数，即Lagrange插值多项式.根据这个多项式，可以估计出缺失时间点的水质指标值.

本文选择四川攀枝花龙洞的2004年第1周至2009年第52周作为训练数据集，2010年第1周至2012年第53周作为测试数据集.采用d=4，即用前4周数据预测下一周数据，则训练数据集为308组，测试数据集为153组.

RVM回归涉及到核函数K(x，x_i)类型的选择，不同的核函数会对预测效果产生不同的影响.本文选择线性核函数_m(x_n)=x_n^m和高斯核函数_m(x_n)=exp{-‖x_m-x_n‖²/2γ²分别对4种水质指标进行预测.在用线性核函数，只需要设置噪声方差σ²一个控制变量，且4种水质指标的噪声方差σ²都设置为0.1².而在应用高斯核函数时，需要设置核函数宽度γ和噪声方差σ²二个控制变量，由于本文RVM回归采用MacKay迭代估计，在迭代估计过程中会出现奇异阵，从而导致矩阵无法求逆，控制变量无法使用交叉验证直接寻优，故需经过多次试验才能得到使预测效果较好的控制变量值.实验中RVM回归算法的最大迭代次数取1000.现将不同水质指标建模过程中试验得到的高斯核函数宽度γ和噪声方差σ²值列于表 1.

表 1(Table 1)

表 1 高斯核函数宽度γ和噪声方差σ2的设置 Table 1 Setting gaussian kernel function γ and noise variance σ2

表 1 高斯核函数宽度γ和噪声方差σ2的设置 Table 1 Setting gaussian kernel function γ and noise variance σ2 水质指标 pH值 DO COD Mn NH 3-N 噪声方差σ 2 0.0009 2 1.21 2 4.84 2 0.0441 2 核函数宽度γ 2.3 5.8 9.18 0.37

由于4种水质指标各自的量纲不同，因此不易以定量方式分析确定RVM回归模型对哪种水质指标的预测效果更好.但根据图 1给出的采用线性核函数时RVM回归模型对4种水质指标的预测结果，可以看出，线性核函数RVM回归模型对pH值的预测效果较好，对DO、COD_Mn和NH₃-N的预测效果虽然略微差一些，但仍可接受.而根据图 2给出的采用高斯核函数时RVM回归模型对4种水质指标的预测结果可知，虽然高斯核函数RVM回归模型对4种水质指标的预测值与原始值(实际值)均能较好地吻合，但DO和COD_Mn的预测效果明显优于对pH值和NH₃-N的预测效果.

图 1(Fig.1)

图 1 线性核函数RVM回归模型对 pH值(a)、 DO(b)、 CODMn(c)及 NH3-N (d)的预测结果 Fig.1 (a) pH value, (b) DO, (c) CODMn and (d) NH3-N prediction results of RVM regression model with linear kernel function

图 2(Fig.2)

图 2 高斯核函数RVM回归模型对 pH值 (a)、 DO (b)、 CODMn (c)及 NH3-N (d)的预测结果 Fig.2 (a) pH value, (b) DO, (c) CODMn and (d) NH3-N prediction results of RVM regression model with gaussian kernel function

由于RVM回归模型在给出预测值时，还可同时获得置信区间，因此能得到预测结果的可信程度，从而为水质监测与管理机构提供更多的参考信息.在本文实验中，RVM回归预测模型的4种水质指标预测值均落在统计学上最常用的置信度95%的置信区间内.

为进一步评估RVM回归水质预测模型的性能，本文以同样的监测数据用SVM回归模型预测相同的水质指标.由于SVM回归模型同样存在核函数的选择问题，为便于比较，在SVM回归模型中同样采用线性核函数和高斯核函数.

本文在比较不同预测模型对同一水质指标的预测效果时，采用了均方误差MSE(Mean Square Error)、相关系数r(Correlation Coefficient)作为评价预测模型性能的指标，其计算公式分别为：

此外，应用SVM回归模型预测前，需先训练SVM.影响SVM回归模型训练算法的控制参数有两个，一个是核函数参数，另一个是惩罚因子.一旦这两个算法控制参数确定了，即可训练SVM，以得到较优的SVM回归模型，并将该模型用于预测.若SVM回归模型采用高斯核函数K(x，x_i)=exp{-γ‖x-x_i‖²}，则核函数参数就是其宽度γ.核函数宽度γ太大会出现过拟合，即对训练样本拟合得较好，而对预测样本泛化能力变得较差；反之，核函数宽度γ太小，会出现欠拟合.与RVM预回归模型不同的是SVM回归模型还需额外确定惩罚因子的大小.惩罚因子用于控制拟合精度惩罚程度，实现拟合精度与算法复杂度的折中.惩罚因子越大，越易出现过拟合；惩罚因子越小，则越易出现欠拟合.惩罚因子及与核函数宽度γ大小的选择与需解决的具体问题以及采用的核函数类型有关，但迄今为止理论上仍无精确决定其数值大小的明确指导.目前最常用的方法是采用交叉验证法寻优，确定它们的较优值.本文采用5折交叉验证对惩罚因子及高斯核函数宽度γ进行寻优，线性核函数及高斯核函数的寻优结果分别如表 2、表 3所示.

表 2(Table 2)

表 2 线性核函数SVM回归模型的惩罚因子交叉验证寻优 Table 2 Cross validation optimization of the penalty factor in SVM regression model with linear kernel function

表 2 线性核函数SVM回归模型的惩罚因子交叉验证寻优 Table 2 Cross validation optimization of the penalty factor in SVM regression model with linear kernel function 水质参数 pH DO COD Mn NH 3-N 惩罚因子 0.65975 0.53589 0.65975 0.5

表 3(Table 3)

表 3 高斯核函数SVM回归模型的惩罚因子及核函数宽度γ的交叉验证寻优 Table 3 Cross validation optimization of the penalty factor and the kernel width γ in SVM regression model with gaussian kernel function

表 3 高斯核函数SVM回归模型的惩罚因子及核函数宽度γ的交叉验证寻优 Table 3 Cross validation optimization of the penalty factor and the kernel width γ in SVM regression model with gaussian kernel function 水质参数 pH DO COD Mn NH 3-N 惩罚因子 0.082469 0.054409 1 0.003906 核函数宽度 γ 2.639 256 1.7411 256

线性核函数和高斯核函数的RVM与SVM回归预测模型对各水质指标预测性能的比较如表 4~7所示，具体从相关系数r、均方误差MSE、训练时间、预测时间和关联向量数nRV或支持向量数nSV(在SVM中与关联向量相对应的是支持向量)这5个方面进行比较.除相关系数r外，其它方面越小越好.

表 4(Table 4)

表 4 pH的预测结果比较 Table 4 Comparison of pH value prediction results

表 4 pH的预测结果比较 Table 4 Comparison of pH value prediction results 预测模型 SVM线性核函数 SVM高斯核函数 RVM线性核函数 RVM高斯核函数 r 0.9983 0.9684 1 0.9864 MSE 0.0034 0.0039 8.4182×10 -6 0.0029 训练时间/s 0.019868 0.015338 0.225173 0.415008 预测时间/s 0.018650 0.004244 0.000013 0.000171 nSV/ nRV 280 286 1 3

表 5(Table 5)

表 5 DO的预测结果比较 Table 5 Comparison of DO prediction results

表 5 DO的预测结果比较 Table 5 Comparison of DO prediction results 预测模型 SVM线性核函数 SVM高斯核函数 RVM线性核函数 RVM高斯核函数 r 0.9991 0.8351 0.9919 0.9938 MSE 0.0007 0.0010 0.0074 0.0052 训练时间/s 0.032478 0.023048 0.274638 0.597479 预测时间/s 0.001494 0.002973 0.000014 0.000277 nSV/ nRV 166 187 2 5

表 6(Table 6)

表 6 CODMn的预测结果比较 Table 6 Comparison of CODMn prediction results

表 6 CODMn的预测结果比较 Table 6 Comparison of CODMn prediction results 预测模型 SVM线性核函数 SVM高斯核函数 RVM线性核函数 RVM高斯核函数 r 0.9997 0.9852 0.9961 0.9977 MSE 0.0032 0.0034 0.0139 0.0049 训练时间/s 0.037534 0.027488 0.296838 0.453513 预测时间/s 0.002842 0.004061 0.000009 0.000189 nSV/ nRV 270 261 3 3

表 7(Table 7)

表 7 NH3-N的预测结果比较 Table 7 Comparison of NH3-N prediction results

表 7 NH3-N的预测结果比较 Table 7 Comparison of NH3-N prediction results 预测模型 SVM线性核函数 SVM高斯核函数 RVM线性核函数 RVM高斯核函数 r 0.9965 0.6201 0.9549 0.9694 MSE 0.0011 0.0017 7.6187×10 -4 4.7872×10 -4 训练时间/s 0.012285 0.018249 0.314046 0.359475 预测时间/s 0.001745 0.003452 0.000009 0.000164 nSV/ nRV 239 231 3 4

对比表 4中的RVM与SVM回归预测结果可知，对于pH来说，若采用同样的核函数，RVM回归模型的相关系数明显大于SVM回归模型，均方误差、预测时间以及关联向量(或支持向量)数都明显小于SVM回归模型.且对比线性核函数和高斯核函数可知，线性核函数的预测效果比高斯核函数好.从表 5和6中可以看出，SVM回归模型对DO和COD_Mn的预测在均方误差MSE上优于RVM，相关系数相差不大，但是预测时间RVM回归模型小得多，SVM的支持向量数是RVM回归模型关联向量数的几十倍甚至上百倍.总的来说两种模型对DO和COD_Mn的预测效果相差不多.由表 7可知，在采用高斯核函数时，RVM回归模型对NH₃-N的预测在均方误差、相关系数、预测时间和关联向量都比SVM回归的要好，在采用线性核函数时，RVM回归模型除了相关系数、训练时间外其它方面比SVM好.

综合表 4~7的预测结果可发现，RVM像SVM一样，有良好的泛化能力，两种回归模型均可得到良好的预测结果.且RVM回归模型的相关系数大多数大于SVM，RVM的关联向量数远远少于SVM的支持向量数，RVM的预测时间比SVM短得多，但4种水质指标的RVM回归模型的训练时间明显比SVM回归模型长.

针对SVM水质预测模型存在支持向量数多，预测时间长，无概率性输出等问题，本文提出了采用RVM回归建立水质预测模型的方法，并分别选择线性核函数模型和高斯核函数的RVM回归模型进行预测.通过与采用对应核函数的SVM回归水质预测模型进行比较可知，RVM模型的预测精度在整体上不低于SVM模型，且RVM给出的是预测的概率分布，能在给出预测的同时给出预测的置信区间，从而为水质监测与管理机构提供更多的参考信息.此外，RVM回归模型具有很强的稀疏性，具有关联向量数少、预测时间短、泛化能力强等优点.因此，RVM回归模型的应用可为水质预测提供一种新的解决思路.