氧化沟(Oxidation Ditch)被普遍认为是一种工艺流程简单、运行管理方便、处理效果稳定、基建投资和运行费用较低且具有较强竞争力的二级生物处理工艺,在我国城镇污水处理厂中受到广泛应用.如漯河市沙南污水处理厂(黄广英等,2010)、福州市洋里污水处理厂(刘伟,2010)、郑州市五龙口城市污水处理厂(许春红等,2006)和滁州市第二污水处理厂(储振华,2014)等一大批污水处理厂都采用了此工艺.
氧化沟内流场结构对氧化沟的运行效果及能耗有着重要影响,因此,要更好地对氧化沟进行设计、运营管理、诊断和故障排除,对其进行水力学特性模拟必不可少.目前,国内外许多学者对此进行了大量的研究.罗麟等(2003)利用三维k-ε紊流数学模型模拟了一体化氧化沟的流速场,采用移动网格技术模拟转刷的转动及沟内动力的来源.张宗才等(2004)采用k-ε紊流数学模型对Carrousel氧化沟的内部及水力学特性进行了分析计算,精确分析了氧化沟内水流的湍动.蒋成义等(2010)对全尺度氧化沟进行了数值模拟,验证了网格的独立性,并比较了使用不同湍流模型(标准k-ε模型、重整化群k-ε模型、可实现性的k-ε模型、雷诺应力模型)对氧化沟流速场的模拟.宋怀辉等(2012)对氧化沟流场进行三维数值模拟,模拟时利用滑移壁面模型定义了转盘的转动和Reynolds应力模型模拟湍流变化,并利用氧化沟流场三维实测数据进行验证.郭丽莎(2010)通过模拟证明了在氧化沟流场的模拟中,污泥相的分布对于流速的影响可忽略,因此,可将污泥和污水作为单一均匀相处理,而液-气两相模型(界面采用自由面)能够很好地模拟氧化沟上层和表层流速,从而减小上层和表层流速的模拟值误差.魏辉等(2002)利用一维河流水质模型模拟了稳态条件下氧化沟流速的变化情况.许丹宇等(2007)采用CFD(Computational fluid dynamics)数值计算和PIV(Particle image velocimetry)测试相结合的方法研究了Carrousel氧化沟的水力学特性.Yang等(2010;2011)模拟对比了两种工况条件下氧化沟的不同运行情况,为优化能耗及出流水质提供了依据;并结合河南省平顶山市污水处理场的氧化沟,用实验及数值模拟的方法研究了Carrousel氧化沟内的流场结构,模拟结果与实验结果吻合度良好.李媛(2005)对圆形Orbal氧化沟的数值模拟计算发现:即使氧化沟设计流速为0.3 m·s-1,也存在污泥沉降淤积的可能性.Stamou等(1997)利用一维河流水质模型预测了稳态条件下氧化沟流速的变化情况.Thakre等(2009)通过改变表面曝气机的速度、浸没深度及叶片扭转角度等关键参数,研究了不同工况下氧化沟内的氧气传质系数.Littleton等(2007)利用给定动力源方程的方法,模拟并研究了转盘曝气的氧化沟流场,但该模型是在实测沟道平均流速基础上建立的,不能准确预测氧化沟内的流速分布.Pawel(2007)利用速度轮廓文件代替动力源来模拟氧化沟流场,尽管这种简化方法大大减少了计算量,但模拟数据较实测数据偏大很多.Le Moullec等(2008)和Vermande等(2007)建立了深水曝气氧化沟的气液两相流模型,研究了氧化沟内液体流态特点及气相体积分数的分布.
然而,目前国内外对氧化沟内流场水力学特性的紊流高级数值模拟相关文献及报道较少.本文基于大涡模拟中的Smagorinsky-Lilly模型,对实验室Carrousel氧化沟模型进行水力学特性模拟,并研究沟内流速和涡量的分布规律.
2 数学模型(Mathematical modeling) 2.1 控制方程大涡模拟中经过匣式滤波函数滤波后的质量守恒、动量守恒方程如下(Rebollo et al., 2014):
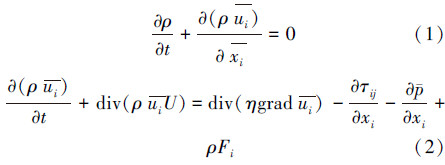
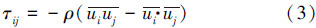
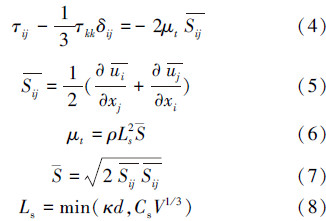
VOF方法(Hirt et al., 1981)通过求解动量方程和追踪通过计算网格的每一相的体积分数来模拟互不混掺的两相或多相流动.VOF法对于相界面的追踪是通过求解各相的相体积分数方程来进行的,对于q相,相体积分数方程表达形式如式(9)所示.
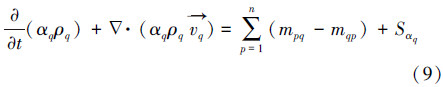

输运方程中的密度是由混合相密度决定的,比如在一个两相流动系统中,如果用下标1和2来代表不同的相,要追踪第2相的体积分数,那么在每个控制体积上密度的表达式如式(11)所示.
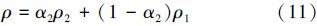
对于有n相的系统,体积分数平均密度用式(12)求得:

本文的模拟对象为一个实验室模型,高25 cm,长度约90 cm,分为6个沟道,每个沟道宽为8.5 cm,有机玻璃板厚度约为1 cm,转弯处均为圆弧.5个推流转轮安装在5个氧化沟弯道处,底部距底面9 cm,转轮直径约8 cm,厚度为2 cm.6个曝气转刷装在直道段,距各自所在直道近端约16 cm,转刷轴距池底18 cm,转刷直径为8 cm,厚度为6 cm.为了更好地描述计算结果及试验验证结果,将转轮、转刷、弯道及直道段进行分区编号,计算区域与编号如图 1所示.
 |
| 图 1 计算区域示意图 (a.三维示意图, b.平面及区域编号示意图) Fig.1 Diagrams of the computational domain |
整个区域网格数为986843个,网格节点约105万.图 2为网格示意图.采用有限体积法(Li et al., 2015)对控制方程进行离散.
 |
| 图 2 网格划分示意图 (a.三维网络示意图, b.平均网格图, c.直道段立面网格图) Fig.2 Grid of the computational domain |
氧化沟顶部敞开区域设为空气进口,入口边界条件采用压力入口,适用于压力为已知、进口流量或流动速度未知的情况,以及可压和不可压流体.为了应用多参考系模型(李志鹏等,2006;宋月兰等,2007),将转轮和转刷叶片转动速度均设为0,而周围流体相对于不动的叶片转动.转动速度为5 r·s-1(所有转刷和转轮1、转轮2和转轮3)和3 r·s-1(转轮4和转轮5),转动方向为从下向上看,转轮1、转轮2和转轮3为顺时针,转轮4和转轮5为逆时针.空气进口处压力设为101.325 kPa,重力加速度设为9.81 m·s-2,因其他因素(如柯氏力等)对模拟结果影响较小,故而忽略.初始转轮淹没深度为2/3,即氧化沟有效水深(H)为19.5 cm.
4.2 求解方法计算中气液两相流模型采用VOF模型追踪自由液面;方程采用有限体积法离散;速度与压力耦合求解使用了压力隐式算子分裂PISO(Pressure-Implicit with Splitting of Operators)算法;对动量方程的离散采用二阶迎风格式.当计算流态达到稳定状态时,即可进行数据的后处理.采用Smagorinsky-Lilly模型作为紊流模型,时间步长设为0.0001 s,算至100 s,流态达到稳定状态.
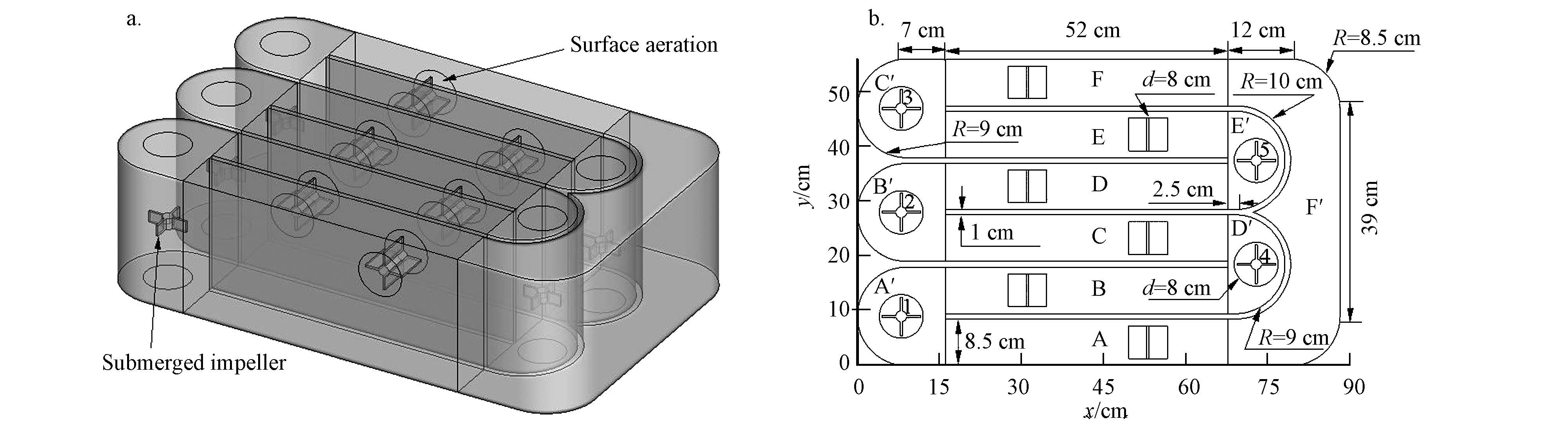
5 实验验证(Experimental verification)为了验证该模拟的准确性,做小试模型试验时对直道C和直道D中x=42cm横断面中轴线(分别记作Line A和Line B)上进行布点检测流速.由于实验条件和检测设备的限制,最底部的测量点由距底面5 cm开始,每2 cm布1个点,共布点16个,具体见图 3.测流速设备为LS300-A便携式光纤流速器.将计算结果中Line A与Line B流速数据与实测结果进行比对,具体如表 1和图 4所示.由表 1可知,在Line A和Line B上均有若干测点模拟流速和实测值的误差较大,但由图 5可知,模拟的流速和实测值沿水深变化趋势一致.因此,本次模拟结果和实验值吻合较好.由此可知,Smagorinsky-Lilly模型能够适用于氧化沟水力学特性模拟,模拟结果具有准确性.
 |
| 图 3 x=42 cm横断面流速监测点分布图 Fig.3 Distribution of flow velocity monitoring points in x=42 cm cross section |
 |
| 图 4 模拟与实测流速沿水深分布比较图 Fig.4 Comparison of simulation and monitoring velocity distributions along water depth |
| 表 1 各测点试验与模拟流速对比 Table 1 Comparison of the simulated and experimental velocities for each monitoring point |
 |
| 图 5 不同深度混合液流线图 (a.z=2 cm, b.z=10 cm, c.z=19.5 cm) Fig.5 Motion patterns of each depth of mixed liquor |
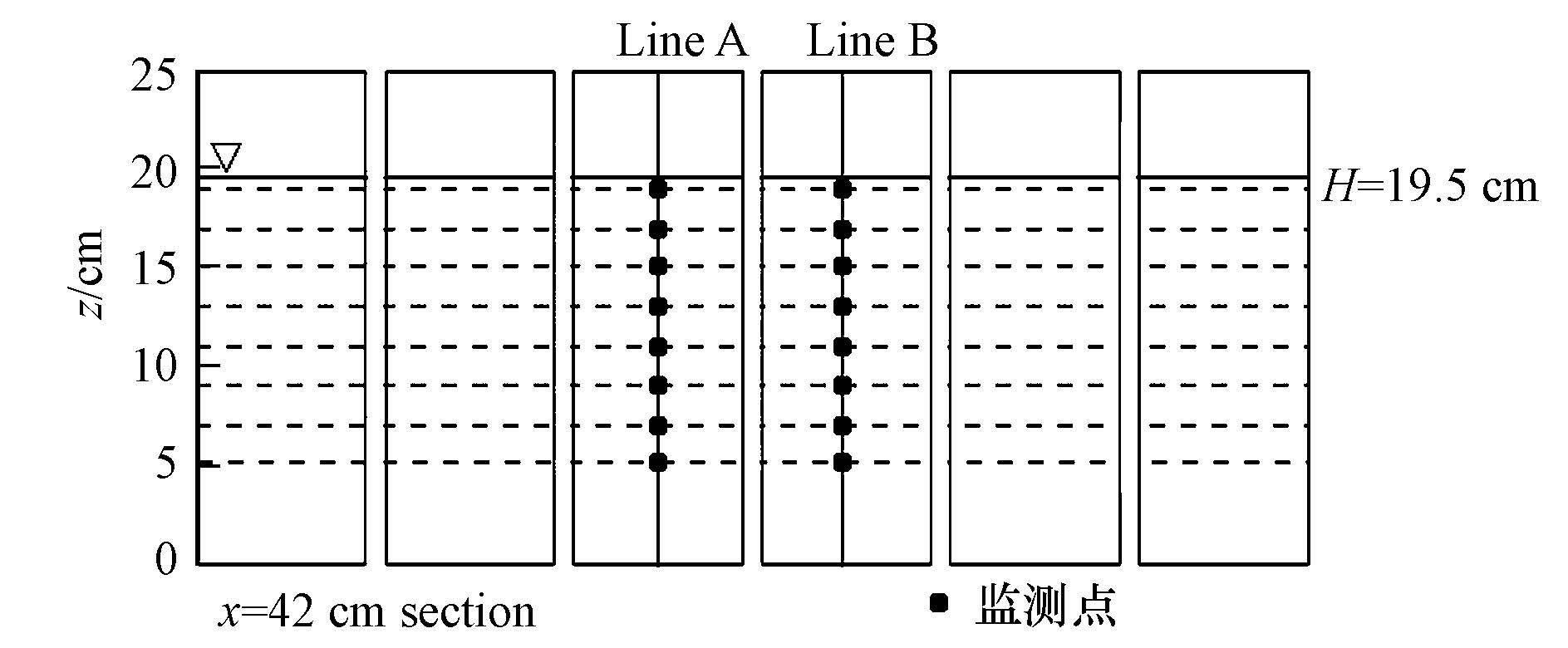
图 5给出计算至稳定后上层(z=19.5 cm截面,即原始水面高度)、中层(z=10 cm截面,即转轮中心高度)及下层(z=2 cm截面)混合液流线图.由图可知,下层混合液在弯道A′、弯道B′和弯道C′内有明显的回流区(A′、B′、C′位置见图 1b),是转轮的转动造成的,并在弯道D′和弯道E′(图 1b)末端有少量回流区;中层混合液由于受到转轮与转刷影响较大,在各个直道的中段及弯道入口处均有明显回流区,然而未见逆流区;上层混合液由于转刷的阻挡,流线较为破碎,回流区和逆流区较为明显.由此可得结论,回流现象主要出现在上中层混合液中,逆流现象主要出现在上层混合液中.局部回流区(如图 5a中小弯道内的回流区)可以使上下层混合液充分混合,对于沟内传质起一定的促进作用;然而过长的逆流区和回流区(如图 5c中直道F内出现的回流区),对于氧化沟内传质极为不利.因此,可将流场结构模拟结果作为氧化沟设计、运行优化和故障诊断的依据,研究如何减少回流区及找出某些运行故障出现的原因,如可通过比较回流区的长短来确定最优转轮半径,以及通过流场结构找出发生污泥沉降现象的原因等.
6.2 三维水面变化趋势显示与分析图 6是计算至稳定后三维水面变化趋势图,图中取水相体积分数为0.5作为水面所在位置.由图可知,水面变化剧烈的位置位于各个弯道及各个直道的转刷所在位置,其有一个共同点就是均有转轮或转刷的推流.在大弯道F及各直道其余位置等无转轮或转刷推流的地方水面变化平缓.因此,可得出结论,转轮转刷的推流作用是造成水面变化剧烈的原因.值得注意的是在各直道转刷下游侧均出现一侧水面高于一侧的现象.
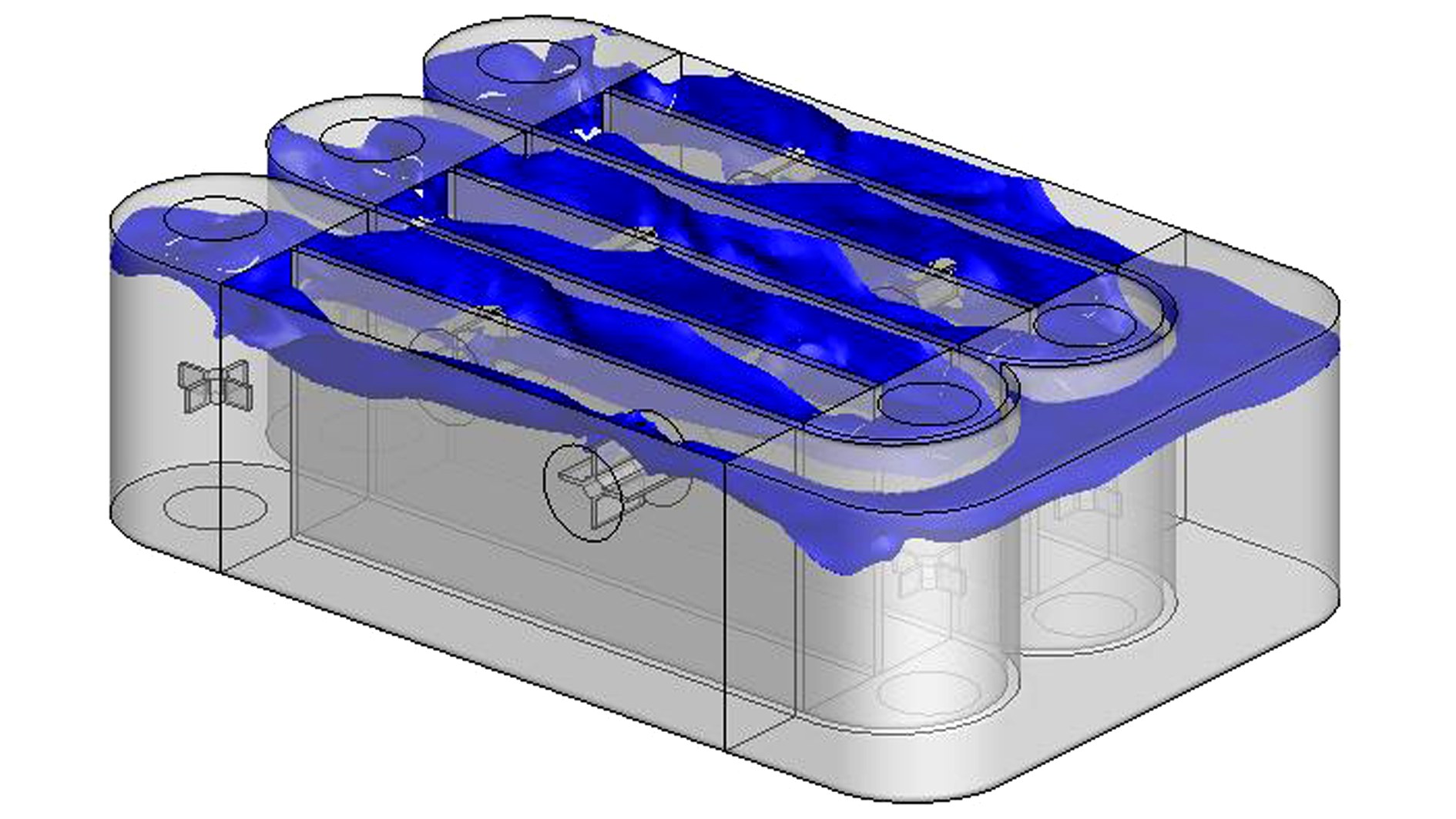 |
| 图 6 三维水面变化趋势图 Fig.6 3-D change trend of the water surface |
图 7为计算至稳定后涡量三维等值面图,图中显示了涡量为70、50、30及10 s-1的涡量等值面图,被等值面包围的区域是大于所给涡量值的区域.从70 s-1涡量等值面图可知,氧化沟中混合液涡量值最高的区域为转轮1、转轮2、转轮3及6个转刷附近,这是由转轮1、转轮2、转轮3及6个转刷转速较快(5 r·s-1),使得周围混合液涡旋流动强烈造成的.从50 s-1涡量等值面图和30 s-1涡量等值面图可知,氧化沟中混合液涡量值较高的区域为转轮4和转轮5附近区域和直道段转刷附近的近壁区域.而从10 s-1涡量等值面图可知,氧化沟中混合液涡量值较低的区域为大弯道F′(图 1b)及其余弯道直道的底层.由此可知,距转轮与转刷较近的区域及转速较快的转轮与转刷区域涡量较大,而远离转轮与转刷的区域涡量较小,说明涡旋由转轮转刷转动产生,并通过混合液的流动传递.结合流场结构可知,涡旋是直道内产生回流区和逆流区的主要原因.可通过对转轮与转刷构造和运行的优化及氧化沟型体的改造减少涡旋在直道段过多的传递而导致的过多回流逆流区的出现及能源的浪费.值得注意的是,由30 s-1涡量等值面图可知,在直道转刷附近存在涡量一侧高于另一侧的现象.
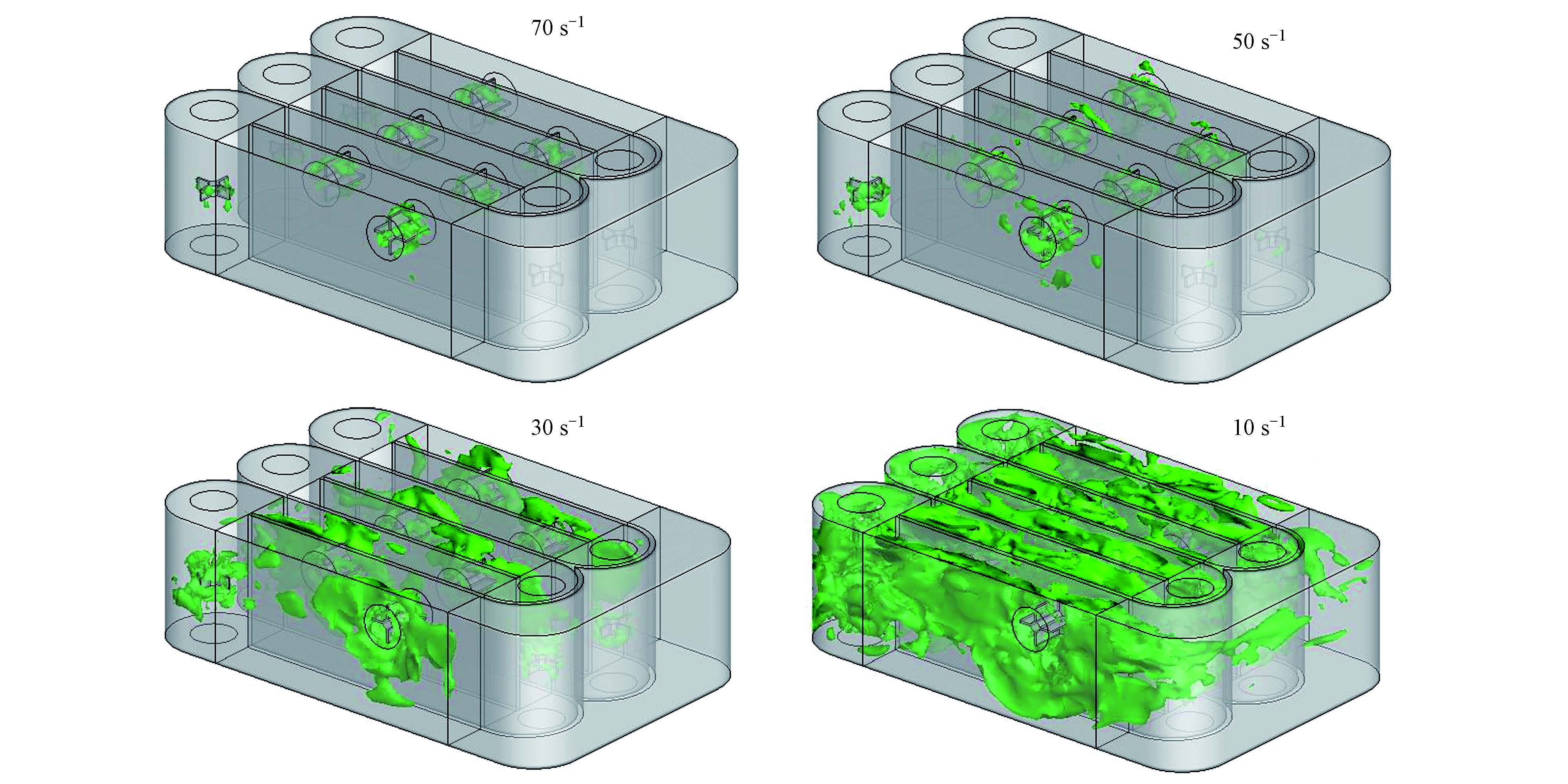 |
| 图 7 三维涡量等值面图 Fig.7 3-D vorticity contour surface |
为了更明确直道段中壁面附近区域与中心区域涡量分布的差异及水面变化趋势和涡量分布的关系,在直道A、直道B和直道C的x=42cm处,即转刷1、转刷2和转刷3下游侧各取3条垂直测线,测线位置与名称如图 8所示,其中,Line1与Line3均距离各自接近的壁面0.5 cm.涡量沿垂线分布如图 9所示,由图可知,在氧化沟直道段转刷下游的中上层混合液中,均存在一侧涡量值大于中心线和另一侧.其中直道A为Line1侧,直道B和直道C为Line3侧.通过与图 6的对比,可得结论:直道段转刷下游水面较高一侧中上层混合液涡量值高于中心和另一侧,该侧应防范因涡量过大和水压过大而对中上层壁面和底层壁面造成的冲蚀.由于该现象的出现与转刷运行密不可分,而转刷在运行中对水流起推动和曝气作用主要是因为叶片在水和空气界面附近的转动,因此,可以断定转刷直径越大,转速越快,该现象表现越明显,然而若转轮叶片转速过慢可能会造成混合液流速过低或者空气不充分.因此,可以通过进一步模拟,对转轮的直径及运行参数(如转速和转刷淹没深度)进一步优化,优化转刷半径、转刷淹没深度和转刷转速,以保证转刷高效节能的运行.
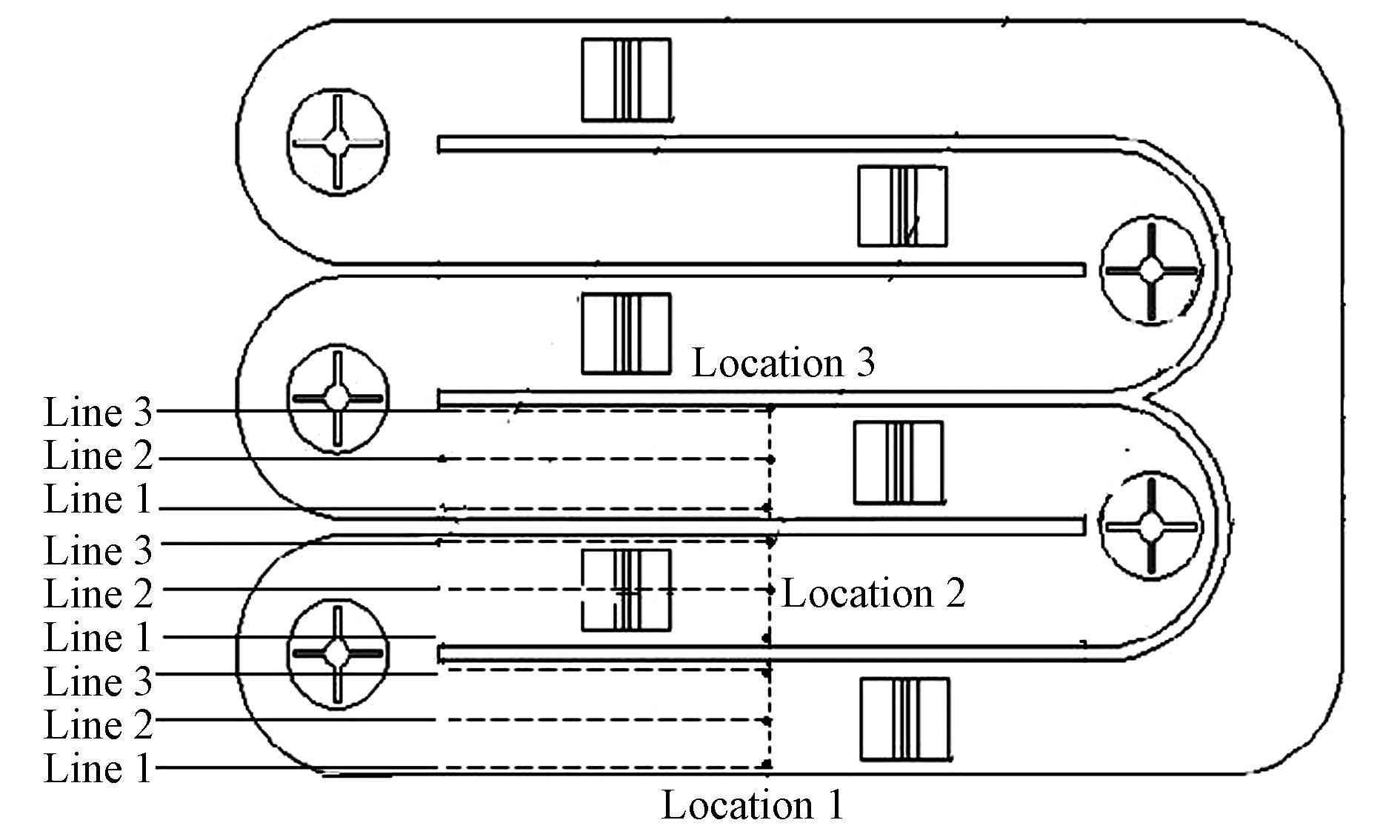 |
| 图 8 测线分布图 Fig.8 Measuring line for vorticity |
 |
| 图 9 涡量沿垂线分布图 Fig.9 Vorticity distribution along each measuring line |
本文基于大涡模拟中的Smagorinsky-Lilly模型,对实验室Carrousel氧化沟模型进行了水力学特性模拟,得出如下结论:
1)通过模型验证,发现Smagorinsky-Lilly模型适用于氧化沟水力学特性数值模拟,模拟精度较高.
2)回流现象主要出现在上中层混合液中,逆流现象主要出现在上层混合液中;转轮与转刷的推流作用是造成水面变化剧烈的原因;距转轮与转刷较近的区域、转速较快的转轮与转刷区域及直道段转刷下游水面较高一侧的中上层区域的涡量较大,应注意防范涡量过大对构筑物本身造成的损蚀.
3)应用大涡模型模拟氧化沟的水力学特性,其结果可进一步为氧化沟的设计、优化改造和故障诊断提供依据.
| [1] | 储振华. 2014. 浅谈污水处理厂超长薄壁氧化沟施工技术[J]. 科技创业家, (3): 3-4 |
| [2] | 郭丽莎. 2010. 卡鲁塞尔氧化沟污水-污泥两相模型及液-气两相模型. 重庆: 重庆大学. 68-75 |
| [3] | Hirt C W, Nichols B D. 1981. Volume of fluid (VOF) method for the dynamics of free boundaries[J]. Journal of Computational Physics, 39(1): 201-225 |
| [4] | 黄广英, 赵若尘, 张金华, 等. 2010. 氧化沟脱氮除磷改造工程实例分析[J]. 环境科技, 23(2): 25-27 |
| [5] | 蒋成义, 黄卫东, 王淦, 等. 2010. 氧化沟流场的计算流体力学数值模型研究[J]. 环境科学与技术, 33(8): 135-140 |
| [6] | Le Moullec Y, Potier O, Gentric C, et al. 2008. Flow field and residence time distribution simulation of a cross-flow gas-liquid wastewater treatment reactor using CFD [J]. Chemical Engineering Science, 63(9): 2436-2449 |
| [7] | Li S Q, Wang P, Lu T. 2015. Numerical simulation of direct contact condensation of subsonic steam injected in a water pool using VOF method and LES turbulence model [J]. Progress in Nuclear Energy, 78: 201-205 |
| [8] | Littleton H X, Daigger G T, Strom P F. 2007. Application of computational fluid dynamics to closed-loop bioreactors: I. Characterization and simulation of fluid-flow pattern and oxygen transfer[J].Water Environment Research,79(6): 600-612 |
| [9] | 李媛. 2005. AIRE—O2充氧机性能浅析与Orbal氧化沟流态测试及三维模拟[D]. 重庆: 重庆大学. 71-80 |
| [10] | 李志鹏, 高正明. 2006. 涡轮桨搅拌槽内流体流动的大涡模拟[C]. 南宁: 第三届全国化学工程与生物化工年会. 10-14 |
| [11] | 刘伟. 2010. 普通型Carrousel氧化沟改造及运行实例[J]. 福建建筑, (2): 125-127 |
| [12] | 罗麟, 李伟民, 邓荣森, 等. 2003. 一体化氧化沟的三维流场模拟与分析[J]. 中国给水排水, 19(12): 15-18 |
| [13] | Pawel G. 2007. CFD modeling of an oxidation ditch[D]. London, UK: Cranfield University. 10-122 |
| [14] | Rebollo T C, Hecht F, Mármola M G, et al. 2014. Numerical approximation of the Smagorinsky turbulence model applied to the primitive equations of the ocean [J]. Mathematics and Computers in Simulation, 99: 54-70 |
| [15] | Smagorinsky J. 1963. General circulation experiments with the primitive equations—I. The basic experiment [J]. Monthly Weather Review, 91(3): 99-164 |
| [16] | 宋怀辉, 何建京, 李志杰, 等. 2012. 氧化沟流场的三维数值模拟[J]. 水动力学研究与进展, 27(2): 174-182 |
| [17] | 宋月兰, 高正明, 李志鹏. 2007. 多层新型桨搅拌槽内气-液两相流动的实验与数值模拟 [J]. 过程工程学报, 7(1): 24-28 |
| [18] | Stamou A I. 1997. Modelling of oxidation ditches using an open channel flow 1-D advection-dispersion equation and ASM1 process description[J]. Water Science and Technology, 36(5): 269-276 |
| [19] | Thakre S B, Bhuyar L B, Deshmukh S J. 2009. Oxidation ditch process using curved blade rotor as aerator[J]. International Journal of Environmental Science & Technology, 6(1): 113-122 |
| [20] | Vermande S, Simpson K, Essemiani K, et al. 2007. Impact of agitation and aeration on hydraulics and oxygen transfer in an aeration ditch: Local and global measurements [J]. Chemical Engineering Science, 62(9): 2545-2555 |
| [21] | 魏辉. 2002. 氧化沟数学模型的初步研究[D]. 长沙: 湖南大学. 59-66 |
| [22] | 许春红, 赵继红, 刘海英. 2006. Carrousel 2000氧化沟工艺的应用实例[J]. 工业用水与废水, 37(5): 84-87 |
| [23] | 许丹宇, 张代钧, 艾海男, 等. 2007. 氧化沟反应器流体力学特性的数值模拟与实验研究[J]. 环境工程学报, 1(12): 20-26 |
| [24] | Yang Y, Wu Y Y, Yang X A, et al. 2010. Flow field prediction in full-scale Carrousel oxidation ditch by using computational fluid dynamics[J]. Water Science and Technology, 62(2): 256-265 |
| [25] | Yang Y, Yang J K, Zuo J L, et al. 2011. Study on two operating conditions of a full-scale oxidation ditch for optimization of energy consumption and effluent quality by using CFD model[J]. Water Research, 45(11): 3439-3452 |
| [26] | 张宗才, 张新申, 张铭让. 2004. 氧化沟水力学分析及流场计算[J]. 中国皮革, 33(11): 22-25 |
 2015, Vol. 35
2015, Vol. 35


