2. 甘肃省气象信息中心, 兰州 730020;
3. 德州学院化学化工学院, 德州 253023
2. Gansu Province Meteorological Information Center, Lanzhou 730020;
3. College of Chemistry and Chemical Engineering, Dezhou University, Dezhou 253023
大气颗粒物已成为我国城市空气污染的主要组分,其中,空气动力学直径小于等于10 μm的可吸入颗粒物本身含有毒有害物质,且由于粒径小,容易吸附有毒有害物质而对人类健康的危害及环境的影响更大(Heal et al., 2012).2013年,国际癌症研究机构将大气颗粒物确定为致癌物质(World Health Organization,2013).由于大气颗粒物来源复杂,因此,准确地解析环境中大气颗粒物来源及贡献率(Srimuruganandam et al., 2012)是制定科学合理的污染预防措施和有效地控制颗粒物污染的基础.常用的大气颗粒物源解析技术包括受体模型和扩散模型(Jorquera et al., 2013).由于受体模型不需要颗粒物的生成、扩散等参数及气象数据,降低了解析的复杂性,成为有效的源解析方法(Taiwo et al., 2014).常用的受体模型可分为需要源成分谱受体模型(以CMB为主)和不需要源成分谱受体模型(以多元统计模型为主)两大类(史国良,2010).实际源解析中,若某区域未建立源成分谱,则要用多元统计模型进行源解析分析(陈分定,2011).多元统计模型要求环境受体数据是连续的、完整的、分布特征基本一致,且需要大量的数据来确保解析结果的稳定性和准确性(Dtton et al., 2010; Andriani E et al., 2011; Pant et al., 2012; Thurston et al., 2011).
但在实际源解析过程中受体数据需要通过样品采集、前处理和测定等多步过程才能获得,工作量大,分析成本高.对于特殊情况下污染源解析的研究,即使每天采样也不能达到多元统计模型对受体数据量的要求.另外,受体数据受污染源和气象条件等因素的影响,污染源和气象条件大幅度变化会导致受体污染物的来源发生变化,表现为受体成分谱不同,如邱立民(2012)研究指出,同一污染时段的不同时间内污染物的来源也不尽相同.若将这些代表污染源或气象条件等发生剧烈变化的数据一并考虑,将会影响源解析结果的准确性和代表性.为此,在源解析时需要将受体数据分类,然后对分布特征基本一致的受体数据进行解析.基于此,本文采用常见的PCA及PMF模型,针对将受体数据分类后存在数据量不够的问题,拟通过正态扩展建立一种既能反映研究区域内污染特征,又能满足多元统计模型对数据量要求的方法(Andriani et al., 2011);同时,针对受体数据中包含代表污染源或气象条件等发生剧烈变化的数据的问题,拟通过53 h算法对各化学成分时间序列中这部分数据进行标记,通过K-均值聚类更加细致地划分不同时间段污染物的特征,然后将每类数据分别进行正态扩展以满足多元统计模型对数据量的要求(Andriani et al., 2011).以上方法的建立可以为受体数据量小、包含代表污染源或气象条件等发生剧烈变化的值且需要用无源成分谱的多元统计方法进行解析的研究提供一种能够得到合理受体数据的方法.
2 数据来源及处理方法(Data and processing methods) 2.1 数据来源采用PMF模型给出的Stockton地区2000年75 d的环境受体数据(Eberly,2005),包含Al、NH4+、Br、Ca、Cl-、Cu、EC、Fe、Pb、Mn、Ni、NO3-、OC、K、Si、Na+、SO42-、Ta、Sn、Ti、V、Zn 22种化学成分和PM2.5的浓度及不确定度.
2.2 处理方法将化学成分浓度作为均值μ,通过不确定度换算得到标准差σ(Norris et al., 2008; 陈静,2012),利用函数normrnd(μ,σ,m,n)产生m个服从N(μ,σ2)的随机数,n为输出矩阵列数,保证浓度不出现负值.选择标准差的0.3、0.5、0.6、0.8、1.0、1.2、1.5、2.0、2.5、3.0和3.5倍作为扩展范围,考察扩展范围对扩展数据的影响;分别将1个受体成分谱正态扩展,得到能满足模型要求的数据量,为考察扩展模拟受体成分谱个数对扩展数据的影响,分别考察扩展成2、3、4、6、8、12和24个模拟受体成分谱的情况.利用PMF和PCA模型进行解析,将原始数据的解析结果作为标准,比较扩展数据和原始数据解析得到的污染源类及计算源贡献率的相对误差(RE)来验证正态扩展的可行性与合理性,其中,RE越小说明扩展数据的解析结果与原始数据的结果越接近,如戴明新等(2008)在研究中将污染源贡献率的RE小于40%作为方法有效性的参考.综合考虑扩展范围和扩展组数确定最佳扩展条件.
53 h算法(杨为钦等,1988)是由Tukey提出来的,其思想是使用中值滤波产生一个平滑估计,然后比较原始数据与估计值的差是否超过给定的阈值,以此来确定原始数据是否超出该组数据的波动范围,如果是则用估计值替代,否则保留原信号.本文通过53 h算法标记出每个化学成分时间序列中被3点Hanning平滑滤波器滤掉的值,即代表污染源或气象条件等发生剧烈变化的值并给出对应的估计值,对标记的值采取全部剔除和将与估计值的RE超过80%的剔除其余替换成估计值两种方式处理,然后通过K-means聚类,求聚到每一类受体数据(设有x1,x2,……,xp个,p为聚类数)的平均值和标准差,分别作为normrnd中的μ和σ,将每类的μ分别扩展成xi个(i=1,2,……,p),按照时间顺序组合成扩展的受体数据.最后利用PMF和PCA模型对剔除/替换代表污染源或气象条件等发生剧烈变化的值前后受体数据解析,通过比较结果,验证53 h算法对各化学成分时间序列中代表污染源或气象条件等发生剧烈变化的值处理的合理性,具体见图 1.
 |
| 图 1 数据处理简图 Fig.1 A diagram of data processing |
将原始数据和各扩展范围下正态扩展得到的受体数据(模型参数设置和原始数据解析一样)分别代入PMF模型进行解析,考察因子个数为4~8,当定义5个因子时得到最佳解析结果.11组正态扩展数据与原始数据经PMF解析得到源的种类一致,均为硝酸盐源、土壤风沙尘源、冶金源、硫酸盐源和燃油源,且最主要的贡献源均为硫酸盐源.不同扩展范围的扩展数据与原始数据解析的源贡献率的RE范围分别为3.16%~35.79%、2.26%~40.11%、0~24.64%、2.31%~20.81%和1.32%~23.68%,具体见图 2.由图 2可知,扩展范围对PMF解析结果有一定影响,但所有的RE均小于40.2%.相比较而言,将0.5倍的标准作为扩展范围时RE最小,即扩展数据与原始数据的PMF解析结果最吻合.
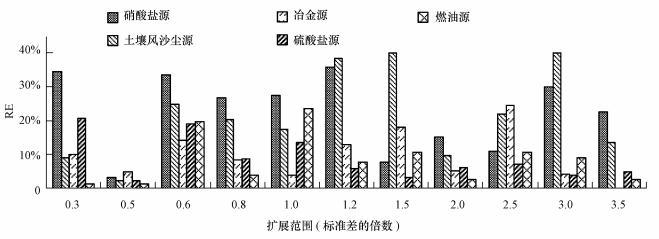 |
| 图 2 不同扩展范围下扩展数据的各源类贡献率相对原始数据PMF解析贡献率的RE Fig.2 RE of source contribution rates of data expansion under each expansion scope and original data by PMF |
选择标准差的0.5倍作为扩展范围,分别将1个原始受体成分谱经正态扩展得到2、3、4、6、8、12和24个模拟受体成分谱,将扩展数据分别代入PMF模型进行解析(模型参数设置和原始数据解析一样).得到的源类与原始数据一致,也是硝酸盐源、土壤风沙尘源、冶金源、硫酸盐源和燃油源,最主要的贡献源也为硫酸盐源. 不同扩展模拟受体成分谱个数下扩展数据与原始数据解析源贡献率的RE分别为2.63%~34.21%、2.26%~39.55%、2.84%~27.01%、0.58%~14.74%和0~35.53%,具体见图 3.由图 3可知,扩展模拟受体成分谱个数对PMF解析结果有一定影响,但所有RE均小于40%.扩展得到6个模拟受体成分谱时RE最小,即扩展数据与原始数据的PMF解析结果最吻合.
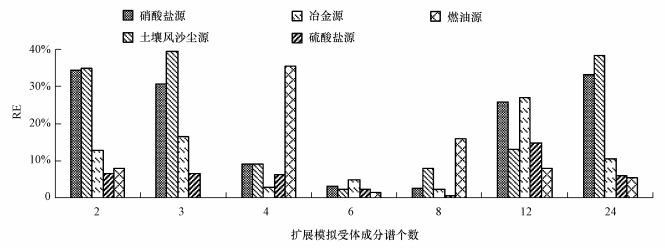 |
| 图 3 不同扩展模拟受体成分谱个数下扩展数据的各源类贡献率相对原始数据PMF解析贡献率的RE Fig.3 RE of source contribution rates of expansion data under each expansion receptor profiles number and original data by PMF |
综上所述,当选择合适的扩展范围和扩展模拟受体成分谱个数时,正态扩展数据通过PMF解析可以得到和原始数据相同的污染源类,且不会影响最大贡献污染源类的判断;各污染源类的贡献率有一定变化,但变化范围均在40%以内.扩展数据能够反映分析时段内原始数据所代表的污染状况.其中,最佳的扩展条件为扩展范围取标准差的0.5倍,扩展模拟受体成分谱个数为6个.
3.1.3 扩展条件验证由于正态扩展的方法的基础数据为各化学成分的浓度和不确定度,与其他因素无关,故此扩展条件具有普遍适用性.为进一步验证该扩展条件的适用性,通过改变化学成分的个数设计以下实验对比验证.
对比实验一:选取10个化学成分(NH4+、Ca、Ni、NO3-、K、Si、SO42-、Ti、V和Zn)及PM2.5作为原始数据,然后分别按照3.1.1节和3.1.2节的方法进行扩展并经PMF解析.得到4个源(硝酸盐源、土壤风沙尘源、硫酸盐源和燃油源),其中,扩展范围取标准差的0.5倍,扩展模拟受体成分谱个数为6个时,原始数据与扩展数据解析得到的各污染源的贡献率的RE差别最小.
对比实验二:选取15个化学成分(NH4+、Ca、Cu、EC、Fe、Ni、NO3-、K、Si、SO42-、Ta、Sn、Ti、V和Zn)及PM2.5为原始数据,然后分别按照3.1.1节和3.1.2节的方法进行扩展并经PMF解析. 得到5个源(硝酸盐源、土壤风沙尘源、冶金源、硫酸盐源和燃油源),同样地,也得到扩展范围取标准差的0.5倍,扩展模拟受体成分谱个数为6个时,原始数据与扩展数据解析得到的各污染源的贡献率的RE差别最小.
经以上实验对比,可以得出正态扩展方法的最佳扩展条件为:扩展范围取标准差的0.5倍,扩展模拟受体成分谱个数为6个.
3.2 PCA模型验证PCA模型能够对大量的观测数据进行统计分析,并且在不损失原有数据主要信息的前提下,对观测数据进行降维,从观测数据的相关系数矩阵出发,得到能够反映原有数据主要信息、对所有数据起到控制作用的几个综合因子(An et al., 2014).
3.2.1 扩展范围确定原始数据和扩展数据进行PCA解析时,均通过KMO和巴特利球体检验,KMO分别为0.829和0.835,大于0.8小于0.9.选择主成分个数4~8,根据主成分的特征根(>1)、累计方差(>75%)和提取公因子方差变化范围小进行判断,当选择7个主成分时,得到最优结果.对于PCA模型,数据扩展范围最大可取标准差的2倍,否则各主成分累计方差小于75%,且解析出来的污染源类发生变化.原始数据与8组正态扩展数据经PCA解析得到的源的种类一致,但与PMF解析得到的污染源类不同,原因为不同的源解析方法对同一组数据能够识别的源项有差别(Lee et al., 2008; Pandolfi et al., 2008;邱立民,2012).扩展数据和原始数据的PCA解析结果均为二次源、燃油源、土壤风沙尘源、燃煤源、冶金源Ⅰ、海盐粒子源和冶金源Ⅱ.不同扩展范围下扩展数据与原始数据解析的贡献率的RE分别为0.39%~20.16%、0.61%~5.52%、1.88%~11.25%、4.29%~28.57%、3.17%~12.7%、0~15.52%和0~1.96%,具体见图 4.由图 4可知,扩展范围对PCA解析结果有一定影响,但所有的RE均小于30%,且取0.5倍标准差作为扩展范围时RE最小,即扩展数据与原始数据的PCA解析结果最吻合.
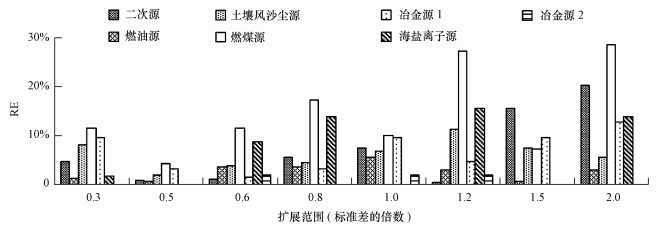 |
| 图 4 不同扩展范围下正态扩展数据的各源类贡献率相对原始数据PCA解析贡献率的RE Fig.4 RE of source contribution rates of expansion data under each expansion scope and original data by PCA |
对各扩展模拟受体成分谱个数下的扩展数据分别进行PCA解析(KMO均大于0.8,小于0.9).累计方差随着扩展模拟受体成分谱个数的增大变化不大,均大于80%,说明7个主成分能够解释污染状况的主要信息.扩展数据解析得到的污染源均为二次源、燃油源、土壤风沙尘源、燃煤源、冶金源Ⅰ、海盐粒子源和冶金源Ⅱ,7组正态扩展数据解析得到各污染源类的贡献率与原始数据的贡献率的RE分别为0.78%~6.59%、0.61%~3.68%、0.62%~9.38%、8.57%~12.86%、0~7.94%、0~8.62%和0~3.92%,具体见图 5.由图 5可知,扩展模拟受体成分谱个数对PCA解析结果有一定影响,但所有的RE均小于14%,且扩展得到6个模拟受体成分谱时RE最小,即扩展数据与原始数据的PCA解析结果最吻合.
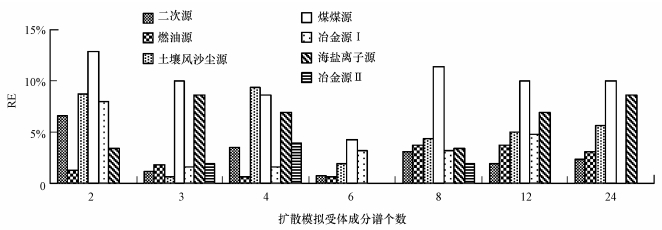 |
| 图 5 不同扩展模拟受体成分谱个数下扩展数据的各源类贡献率相对原始数据PCA解析贡献率的RE Fig.5 RE of source contribution rates of expansion data under each expansion receptor profiles number and original data by PCA |
为了更好地说明正态扩展数据的合理性,本文还进行“对75 d受体数据→求均值→正态扩展得到75 d扩展数据→验证”,结果表明,经过以上处理的扩展数据经PMF和PCA运行后得不到合理的结果.分析原因可能是受体数据中存在代表污染源或气象条件等发生剧烈变化特征的值,需要对其处理后才能进行分析.
引入53 h算法,将标记为代表污染源或气象条件等发生剧烈变化特征的值所在的受体成分谱删除后,再进行以上分析,结果还是不理想,分析原因可能是因为扩展模拟受体成分谱个数太多,数据失真.为此,本文进行以下处理.
4.1 删除处理删除53 h算法标记出的代表污染源或气象条件等发生剧烈变化的值所属的受体成分谱,剩余44 d数据(原始数据).对这44 d浓度数据进行K-均值聚类,得到20类,分别求出各类的均值和标准差,经正态扩展,然后按照时间顺序组合形成44 d正态扩展数据.不确定度也采用相同的方法处理.
4.1.1 PMF模型验证将44 d原始数据和相应的扩展数据代入PMF进行解析.考察因子个数为4~8,当定义5个因子时得到最佳解析结果.原始数据和扩展数据经PMF解析得到源的种类一致,均为燃油源、土壤风沙源、冶金源、硫酸盐源和硝酸盐源,且最主要的贡献源为硫酸盐源.扩展数据与原始数据PMF解析的贡献率的RE分别为77.78%、2.34%、26.92%、0.55%和212.68%,具体见图 6.
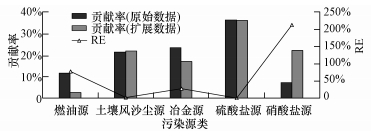 |
| 图 6 44 d原始数据与正态扩展数据PMF解析的源贡献及两者间的RE Fig.6 Source contribution rates and RE of expansion data and 44 days′ original data by PMF |
由图 6可知,删除代表污染源或气象条件等发生剧烈变化特征的值后不会影响PMF模型对主要污染源的判断.除硝酸盐源和燃油源的源贡献率差别较大,其余3个污染源类的源贡献率的RE均小于50%,其中,燃油源和硝酸盐源贡献率的RE较大的原因可能为计算得到表征燃油源的Ni、V和表征硝酸盐源的NO3-的标准差较大,使得正态扩展后的数据与原始数据中化学成分的分布差别较大,导致解析结果差别较大.
4.1.2 PCA模型验证对剔除代表污染源或气象条件等发生剧烈变化特征的值后的44 d浓度数据进行PCA解析,发现无论是原始数据还是扩展数据,KMO均小于0.7,不适合作PCA解析.分析原因为对于PCA模型,44 d的数据偏少,解析时不能得到合理的结果,暂不考虑.
4.2 替换处理按照图 1将代表污染源或气象条件等发生剧烈变化特征的值替换后,得到61 d浓度数据.然后进行聚类(得到18类)、求均值和标准差、正态扩展及按照时间顺序组合,形成61 d的扩展数据.
4.2.1 PMF模型验证将61 d的原始数据和扩展数据代入PMF模型,考察因子个数为4~8,当定义5个因子时得到最佳解析结果.原始数据和扩展数据经PMF解析得到的污染源的种类一致,均为燃油源、土壤风沙源、冶金源、硫酸盐源和硝酸盐源.扩展数据与原始数据解析的贡献率的RE分别为136.76%、13.86%、20.54%、11.39%和8.00%,具体见图 7.由图 7可知,替换处理后不会影响PMF模型对主要污染源的判断.除燃油源的贡献率差别较大,其余污染源类的源贡献率的RE均小于30%,且结果明显好于直接删除处理的情况.
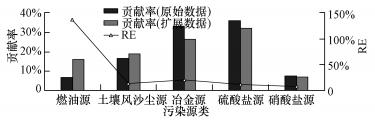 |
| 图 7 61 d原始数据与正态扩展数据PMF解析的源贡献及两者间的RE Fig.7 Source contribution rates and RE of expansion data and 61 days′ original data by PMF |
将61 d原始数据和扩展数据代入SPSS中进行PCA解析,通过KMO和巴特利球体检验(KMO分别为0.765和0.825),选择主成分个数4~8,通过分析主成分的特征根(>1)、累计方差(>75%)和提取公因子方差(变化范围小)进行考察,当选择7个主成分时,得到最优结果.扩展数据与原始数据解析得到污染源种类除第五主成分以外均一致,分别为二次源、燃油源、土壤风沙尘源、燃煤源、海盐粒子源和冶金源Ⅱ.对于第五主成分,判断为不同的源类,原始数据判断的源类为冶金源Ⅰ,扩展数据判断的源类为机动车尾气尘源.扩展数据与原始数据解析源贡献率的RE分别为9.68%、23.31%、1.77%、8.06%、29.31%、7.27%和35.29%,具体见图 8.由图 8可知,扩展数据与原始数据经PCA解析后7个源类的贡献率基本一致.所以,经替换处理后,正态扩展数据和原始数据的PCA解析结果除个别贡献不大的源类的判断不一致外,其余无论是污染源的判断还是源贡献率均基本一致.
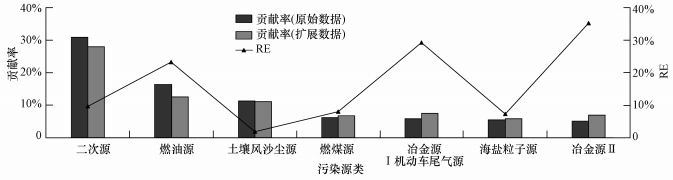 |
| 图 8 61天原始数据与正态扩展数据PCA解析的源贡献及两者间的RE Fig.8 Source contribution rates and RE of expansion data and 61 days′ original data by PCA |
1)对受体数据进行正态扩展,得到扩展数据.利用PMF和PCA模型验证得出,正态扩展产生的扩展数据既能满足多元统计模型对受体数据量的要求,也能较为准确地反映原始数据所代表的污染状况.其中,扩展范围和扩展模拟受体成分谱个数是影响扩展数据与原始数据拟合程度的两个因素,最佳扩展条件为:扩展范围取标准差的0.5倍,扩展模拟受体成分谱个数为6个.
2)将53 h算法引入,标记出每个化学成分时间序列中代表污染源或气象条件等发生剧烈变化的值并给出对应的估计值,将相对于估计值的RE超过80%的标记值剔除,其余替换成估计值,扩展数据的PCA解析结果与原始数据的除个别贡献小的源类判断不同外,其他源类的判断和源贡献率基本一致,能够很准确地得到主要贡献的污染源类及贡献率;若将标记值全部剔除,由于数据量太少,不适合做PCA解析,仅通过PMF验证,且扩展数据与原始数据的解析结果中污染源类的判断一样,只是个别贡献较小的污染源类的源贡献率差别较大.实际中推荐使用53 h算法标记化学成分时间序列中的代表污染源或气象条件等发生剧烈变化特征的值,并结合给出的估计值,考察标记值与估计值的RE,对不同大小标记值采取替换和剔除两种处理方式,会得到更合理的解析结果.
3)本文提出扩展方法可以解决受体数据量小、数据中包含代表污染源或气象条件等发生剧烈变化特征的值而且需要用无源成分谱的多元统计方法解析无法给出结果的情况下源解析.
| [1] | An J L, Zhu B, Wang H L, et al. 2014. Characteristics and source apportionment of VOCs measured in an industrial area of Nanjing, Yangtze River delta, China[J]. Atmospheric Environment, 97: 206-214 |
| [2] | Andriani E, Caselli M, de Gennaro G, et al. 2011. Synergistic use of several receptor models (CMB, APCS and PMF) to interpret air quality data[J]. Environmetrics, 22(6): 789-797 |
| [3] | 陈分定. 2011. PMF、CMB、FA等大气颗粒物源解析模型对比研究[D]. 长春: 吉林大学 |
| [4] | 陈静. 2012. 西安市大气和土壤中多环芳烃的污染特征研究[D]. 西安: 西安建筑科技大学 |
| [5] | 戴明新, 刘长兵, 胡焱弟, 等. 2008. 径向基函数神经网络在个体颗粒物暴露来源解析中的应用[A]//中国颗粒学会. 中国颗粒学会第六届学术年会暨海峡两岸颗粒技术研讨会论文集(下)[C]. 上海: 华东理工大学. 614-619 |
| [6] | Dtton S J, Vedal S, Piedrahita R, et al. 2010. Source apportionment using positive matrix factorization on daily measurements of inorganic and organic speciated PM2.5[J]. Atmospheric Environment, 44(23): 2731-2741 |
| [7] | Eberly S. 2005. EPA PMF 1.1 user's guide[Z]. Washington: US Environmental Protection Agency National Exposure Research Laboratory |
| [8] | Heal M R, Kumar Pu,Harrison R M. 2012. Particles, air quality, policy and health[J]. Chemical Society Reviews, 41(19): 6606-6630 |
| [9] | Jorquera H, Barraza F. 2013. Source apportionment of PM10 and PM2.5 in a desert region in northern Chile[J]. Science of the Total Environment, 444: 327-335 |
| [10] | Lee S, Liu W, Wang Y H, et al. 2008. Source apportionment of PM2.5: Comparing PMF and CMB results for four ambient monitoring sites in the southeastern United States[J]. Atmospheric Environment, 42(18): 4126-4137 |
| [11] | Norris G, Vedantham R, Wade K, et al. 2008. EPA Positive Matrix Factorization (PMF) 3.0 Fundamentals & User Guide[Z]. Washington: EPA Office of Research and Development, DC 20460 |
| [12] | Pandolfi M, Viana M, Minguillón M C, et al. 2008. Receptor models application to multi-year ambient PM10 measurements in an industrialized ceramic area: Comparison of source apportionment results[J]. Atmospheric Environment, 42(40): 9007-9017 |
| [13] | Pant P, Harrison R M. 2012. Critical review of receptor modelling for particulate matter: a case study of India[J]. Atmospheric Environment, 49: 1-12 |
| [14] | 邱立民. 2012. 城市大气中颗粒物源解析的不确定性研究[D]. 长春: 吉林大学 |
| [15] | 史国良. 2010. 大气颗粒物来源解析复合受体模型的研究和应用[D]. 天津: 南开大学 |
| [16] | Srimuruganandam B, Nagendra S M S. 2012. Source characterization of PM10 and PM2.5 mass using a chemical mass balance model at urban roadside [J]. Science of the Total Environment, 433: 8-19 |
| [17] | Taiwo A W, Harrison R M, Shi Z B. 2014. A review of receptor modelling of industrially emitted particulate matter[J]. Atmospheric Environment, 97: 109-120 |
| [18] | Thurston G D, Ito K, Lall R. 2011. A source apportionment of U.S. fine particulate matter air pollution[J]. Atmospheric Environment, 45(24): 3924-3936 |
| [19] | World Health Organization. 2013. IARC: Outdoor air pollution a leading environmental cause of cancer deaths[EB/OL]. http://www.iarc.fr/en/media-centre/iarcnews/pdf/pr221_E.pdf |
| [20] | 杨为钦, 顾岚. 1988. 时间序列分析与动态数据建模[M]. 北京: 北京理工大学出版社 |
 2015, Vol. 35
2015, Vol. 35


