相对于点源污染，非点源污染由于其自身的隐蔽性和难以量化性，备受研究人员的关注并得到了广泛研究(Dowd et al.,2008；Zhang et al.,2011；白凤娇等，2012；刘亚群，2014).而作为坡面径流、壤中流等输送污染物的重要载体，土地利用则成为研究非点源污染与地表水质关系的关键对象.

纵观土地利用对地表水质影响的定量分析研究，从分析方法上看，应用最为广泛的是基于统计学的方法，包括相关分析、聚类分析、主成分分析、线性回归模型、指数模型等.例如，官宝红等(2008)、孟祥巍等(2014)分别利用相关分析、普通线性回归模型评价了不同土地利用类型对水质影响的显著性；曹芳芳等(2013)通过Spearman相关分析、指数模型定量计算出土地利用结构与水质指标的关系，并利用层次聚类法，研究了流域内水质指标的相似性分布；Ahearn 等(2005)则采用优化的线型混合效应模型，讨论了不同水文年及上下游地区土地利用、人口密度对水质的影响；Tran 等(2010)在分析河流不同邻近度下土地利用类型对水质的影响时，用到了主成分分析、相关分析及断点回归等技术；Wang 等(2013)运用聚类分析及逐步线性回归模型，探讨了不同人为干扰梯度下，土地利用与水质的关系.该类研究结果普遍表明，与人类活动关系密切的土地利用类型，如农用地、城镇建设用地、商业用地、工矿用地等，通常与河流水质污染物(如总氮、总磷、氨氮等)浓度呈正相关关系，而受人类活动影响较小的林地、草地则多与水体污染物浓度呈负相关关系.

以上传统统计方法如线性回归模型、指数模型的应用均基于同一个假设前提：即在整个研究区域内，水质指标与土地利用类型的关系是保持稳定的，不随空间位置改变而发生变化.这是一种全局统计的方法，回归方程在很大程度上表现为现有关系混合的平均值.而实际中，随着研究区域的不同，同一土地利用类型对水质指标的影响也在发生变化.例如，王瑶等(2012)在关于北京市土地利用结构与水质关系的研究中发现，农用地与高锰酸盐指数、氨氮浓度呈正相关；而在孙金华等(2011)关于滇池流域的研究中发现，农用地与TN、氨氮呈负相关.实际上，水质与土地利用往往表现出局部变化特征，即使在同一流域的不同位置，其相应社会经济特征、主要土地利用方式也会不同，导致影响该局部地区水质的第一因素发生改变，同一种土地利用类型对水质的影响有时甚至会呈现相反的关系.此时若依然采用全局模型，将掩盖可能具有意义的局部特征.Williams 等(2005)的研究结果表明，在美国Massachusetts东部，农用地与水质指标Ca、Na、Mg等表现为显著正相关；而针对同一地区，Tu等(2008)运用普通最小二乘模型的研究结果却发现，农用地与这3种指标显著负相关.可见，使用全局统计模型所得结果有时并不可靠.

地理加权回归(Geographically Weighted Regression，GWR)模型(Fotheringham et al.,1996；2002)作为一种局部统计方法，被Tu等(2008)首次引入到评估土地利用与水质关系的研究中，并得到了优于传统线性回归模型(如Ordinary Least Squares，OLS)的结果.该模型通过将数据的空间位置嵌入到回归参数之中，以探索自变量与因变量在空间范围内的变化关系，有效地解决了空间非平稳性(Fotheringham et al.,2002)的问题；同时，针对传统统计方法中难以处理的空间数据自相关性(Brown et al.,2012)，GWR模型也进行了考虑.作为一门新兴技术，GWR模型已被应用到多个领域，如疾病健康研究(Nakaya et al.,2005)、犯罪频发地区调查(Cahill and et al.,2007)、森林损失评估(Pineda et al.,2010)、地下水受土地利用影响评价(Javi et al.，2014)等.

然而，在以往应用GWR模型分析土地利用对地表水质影响的研究中(Tu et al.,2008; Tu，2013；Pratt et al.，2012)，侧重点往往是对比GWR模型相对其它模型的优势及定量描述GWR结果，却很少有对GWR回归结果出现空间变化的具体原因进行阐述.为此，本研究基于GWR模型，采用子流域分析的方式，同时结合水质污染空间分布特征来探讨不同土地利用类型对地表水质的影响，主要尝试解决以下问题：①在不同子流域或测站点，土地利用类型对水质影响的空间分布特征如何，在何处正相关，何处负相关？何处影响大，何处影响小？并对此现象进行解释；②对比GWR模型与传统线性回归模型的性能，并检验GWR模型在处理空间自相关中是否具备优势.

本文选取温瑞塘河温州段为研究区域(120°27′~120°46′E，27°51′~28°02′N)，流域面积371.1 km²(图 1).温瑞塘河位于浙江省东南沿海瓯江和飞云江之间的温瑞平原地区，河道北起温州市鹿城区，南至瑞安市城关东门白岩桥，河网总长1178 km，主河道长33.9 km，水面面积22 km²，流域总面积近740 km²，河网密集.温瑞塘河流域属亚热带季风气候，多年平均降雨量为1818 mm，其中，70%的降水集中在4—9月的丰水期.塘河年径流量9.1亿m³，对温州市农田灌溉、水产养殖、城市排洪及居民、工业用水有重要作用.

图 1(Fig.1)

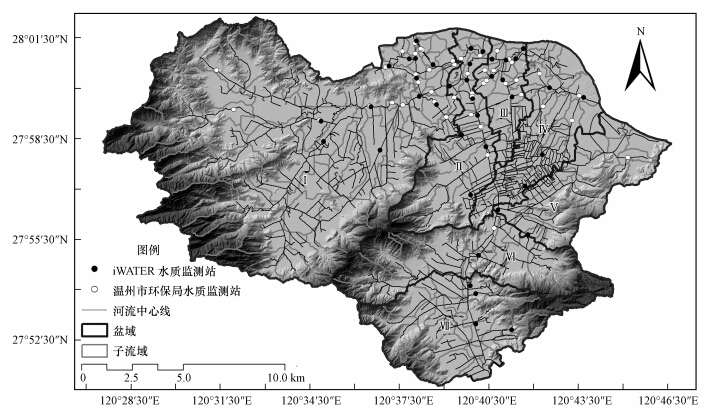图 1 温瑞塘河流域温州段水质监测点布设及盆域划分 Fig.1 Location of monitoring sites and basin area in Wen-Rui Tang River

根据河网分布和流域地形特征，将研究区域划分为7个流域盆地.其中，盆域Ⅰ被山地环绕，土地利用类型以灌木林、果林主导的林地及农用地为主；Ⅱ、Ⅲ、Ⅳ、Ⅴ区北部是温州市主城区，主要用地为城市建设用地等，南部为三垟湿地，湿地陆域面积以人工栽培果木和城镇建设用地为主；Ⅵ、Ⅶ区主要为林地和农田，此处河网多经帆游(丽岙镇)进入瑞安市境内，向南汇流至飞云江并最终注入东海.

截至2013年底，温州市常住人口达919.7万，10年内增长了18.7%，国民经济三次产业结构比为2.9 ∶ 50.3 ∶ 46.8.根据温州市水利局《2012年温州市水资源公报》统计，2012年温州平原河网水质达到地表水环境质量Ⅲ~Ⅳ类标准的河长为31.8 km，占评价总河长的16%，其余断面水质皆为劣Ⅴ类.Mei等(2014)通过对该地区11年水质时空变化特征的分析发现，氮污染是温瑞塘河流域最主要的污染问题，温瑞塘河水污染现状不容乐观.

研究共选取70个水环境监测断面数据进行分析，分析时段为2008—2010年.其中，30个断面由温州市环保局所设，采样间隔为4~8周；其余40个断面由本研究中心所设，每月进行1次采样，用以对数据进行补充.入选水质指标包括pH、溶解氧(DO)、总氮(TN)、氨氮(NH⁺₄-N)及电导率(EC).所有采集水样均按照国家《地表水环境质量标准》(GB3838—2002)和《水和废水监测分析方法》进行测定与分析.

分别统计每个监测断面不同水质指标实测结果的年均值，并针对每种水质指标进行Kolmogorov-Smirnov检验，为保证后期模型分析过程的准确性，采用自然对数变换的方法对数据进行处理.

以分辨率为0.5 m的温州市航空影像为数据源，将解译后的96种详细土地利用类型重分类为7种一级类别：农用地、绿地(园地、林地、草地及城市绿化带)、商服用地(商务金融用地、行政办公用地、文化娱乐用地、医疗卫生用地及市政公用设施用地等)、交通用地、工矿用地、住宅用地和水域(图 2).由于流域内未利用地如裸岩石砾地、迹地等其斑块数量极少且均处于山地，为统计方便统一合并到住宅用地.

图 2(Fig.2)

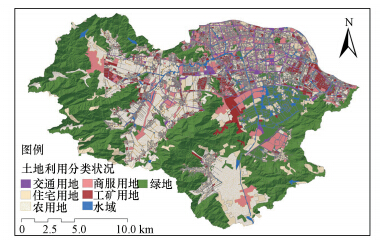图 2 研究区域内7种土地利用类型空间分布 Fig.2 Spatial distribution of the 7 types of l and use in study area

以分辨率为5 m的温州市DEM为数据源，利用ArcGIS 10.2软件下的水文分析模块计算流域栅格的流向与流量，并提取出流量大于10000(栅格Value值，无量纲)的栅格得到河网，通过盆域分析确定出7个出水口不同的流域盆地(图 1中Ⅰ~Ⅶ)；利用Arc Hydro Tools生成河网支流所在的集水多边形并与盆地要素叠加，消除碎屑多边形后，以流域盆地边界为基准，对面积小于10万m²且相 互毗邻的集水多边形进行合并，得到201个子流域.最后，利用ArcGIS统计分析工具计算得到每个子流域内不同土地利用类型的面积及百分比(图 3).

图 3(Fig.3)

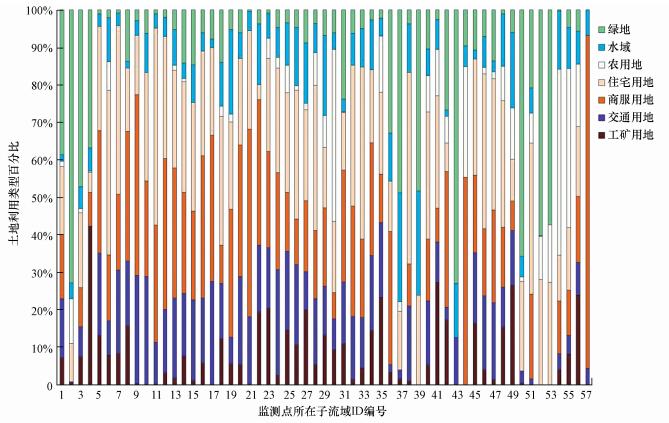图 3 监测站所在的57个子流域土地利用结构比较 Fig.3 Comparison of l and use structure in the 57 sub-watershed where monitoring sites are located

原始数据为温州市每个行政区划(街道为单位)下的2010年第六次全国人口普查数据，为了得到每个测站点的人口密度，采用如下方法：①查找每个行政区划的质心位置，赋予其对应区划的人口数；②采用Kernel算法(牟乃夏等，2012)，由质心点内插出人口密度栅格图；③提取各测站所对应栅格的Value值，即得到该点人口密度.

传统回归模型如普通线性回归模型假定回归参数在整个研究区域保持稳定一致，与样本的空间位置无关，回归参数的估计通常采用最小二乘估计方法求解极值得到.作为一种全局统计，该方法往往忽略了不同地区回归参数的变异性.地理加权回归模型作为普通线性回归模型的扩展，将数据的空间位置嵌入到回归参数之中(Fotheringham et al.,2002)，通过求得局部参数评估自变量与因变量关系在空间尺度上的变动，是一种局部统计模型.其基本形式为：

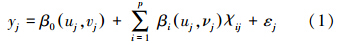
式中，(u_j，ν_j)为第j个采样点的坐标，β_i(u_j，ν_j)为自变量χ_i在j点处的局部回归系数，β₀(u_j，ν_j)及ε_j分别为模型在j点处的回归常数和误差项.针对回归参数β_i(u_j，ν_j)的估计，可通过式(2)达到最小来估计(Brunsdon et al.,1998;覃文忠，2007).

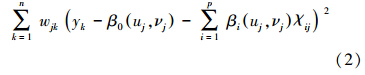
式中，w_jk为回归点j与其它已知观测点k之间的距离衰减函数，其基本假设为距离j点越近的观测点对求解局部回归参数的重要性越大，越远的观测点重要性越小.w_jk作为空间权重矩阵，是地理加权回归模型的核心，计算方法包括距离阈值法、Gauss函数法及bi-square函数法等(覃文忠，2007)，其中，Gauss空间权函数因其普适性而得到广泛应用，本研究即采用此方法，函数形式为：

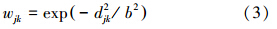
式中，d_jk为观测点j、k之间的距离；b为描述权重与距离之间函数关系的非负衰减参数，也称为带宽(Fotheringham et al.，2002)，当观测点间的距离大于b值时，权重w_jk迅速趋近于0，保证远距离的点对回归点处的参数估计影响最小.关于b的设置，ArcGIS10.2中提供固定带宽和自适应带宽两种形式，前者查找的是最佳距离，后者计算的则为最佳邻近点个数.

为避免由于多重共线性而导致GWR模型出现设计错误，本研究选取单独一种土地利用类型作为解释变量，分别和不同水质指标构建普通最小二乘模型(OLS)与GWR模型，两者分别由SPSS及ArcGIS10.2构建，共得到80个模型.在带宽的选择上，与文献(Tu et al.,2008;Tu，2013)所用自适应带宽不同，本研究通过对比验证，发现固定带宽法在构建温瑞塘河流域的GWR模型中具备更好的优势.

针对GWR和OLS模型的评价，本文主要从模型精度和处理空间自相关能力两方面进行分析.首先，选取校正R²及AIC_c(Akaike信息准则)(Tu et al.,2008)两个指标对两模型进行对比，以确定GWR模型是否优于普通线性回归模型：R²越大表明自变量对因变量的解释程度越高，AIC_c作为评价模型精确度及复杂性的指标，取值越低表明模型预测能力越好，通常两模型AIC_c的差值大于3，则可认为具有较低AIC_c的模型更佳(Brown et al.,2012).

其次，根据水质实测值与回归值的残差分别计算两模型的全局Moran′s I指数值，以对比GWR和OLS模型处理空间自相关的能力.如果模型较好，则其偏高估计值和偏低估计值将随机分布；残差若存在空间聚类，则表明模型可能丢失了某个关键解释变量.在GIS中，Moran′s I是反应空间数据聚散与否的有效指标，其计算公式如下：

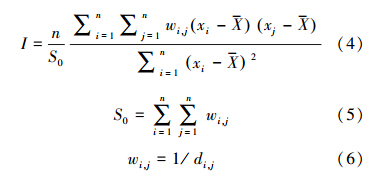
式中，x_i、x_j分别为要素i和邻近要素j的值，w_i，j是两者之间的空间权重，此处定义为要素i和j之间距离d的倒数；n是要素的个数，S₀是所有空间权重的聚合.全局Moran′s I从-1到1进行取值，在统计显著时，若I 为0则数据集为随机分布；I为正，表明存在聚类趋势的空间自相关，I为负表示离散趋势，I值越接近于0，表明模型处理空间自相关的能力越强.本研究中，校正R²、AIC_c及全局Moran′s I均在ArcGIS 10.2中分析并进行显著性检验.

针对研究区域内70个监测站，计算其对应子流域(部分测站位于同一子流域内)土地利用与不同水质指标的Spearman相关系数(表 1).由表 1可知，交通用地、商服用地及人口密度均与DO显著负相关，前两者又与TN、NH⁺₄-N显著正相关；水域则与TN、NH⁺₄-N显著负相关，这可能是由于随着水体面积的增加，其对水质污染物起到了一定的稀释作用；农用地与TN、NH⁺₄-N、EC均表现为负相关，表明随着农用地的增多河流水质也在提高，这与很多同类研究结果不同(王娇等，2012；曹芳芳等，2013).孙金华等(2011)对此现象解释为工矿用地等城市建设用地掩盖了农用地本身对河流的污染贡献.然而，具体原因有待进一步说明.

表 1(Table 1)

表 1 水质指标与土地利用、人口密度的Spearman相关分析 Table 1 Spearman correlations between water quality and l and use，population density indicators

表 1 水质指标与土地利用、人口密度的Spearman相关分析 Table 1 Spearman correlations between water quality and l and use，population density indicators 交通用地 住宅用地 农用地 商服用地 工矿用地 水域 绿地 人口密度 注：*p<0.05，**p<0.01. DO -0.428** -0.061 0.221 -0.363** -0.086 0.220 0.125 -0.390** TN 0.312** 0.071 -0.393** 0.288* -0.012 -0.360** -0.085 0.039 NH+4-N 0.342** 0.074 -0.420** 0.280* -0.036 -0.324** -0.054 -0.010 pH 0.378** 0.447** -0.190 0.090 -0.058 0.157 -0.261* 0.023 EC 0.058 0.211 -0.262* 0.015 -0.118 -0.075 0.000 -0.298*

由于GWR模型在局部回归系数的计算中对相邻要素赋予了一定权重，因此，在分析系数变化时必须考虑周围子流域的情况.受篇幅所限，此处未全部列出40个GWR模型结果，仅挑选出具有代表性且显著相关的TN与农用地、TN与交通用地、DO与人口密度共3组模型进行详细讨论，对应OLS模型如表 2所示.

表 2(Table 2)

表 2 所选3种OLS模型结果 Table 2 Results of the 3 selected OLS models

表 2 所选3种OLS模型结果 Table 2 Results of the 3 selected OLS models 因变量y 自变量x OLS方程 p lnTN 农用地比例 y = 2.428-0.016x 0.016 lnTN 交通用地比例 y = 1.935+0.029x 0.001 lnDO 人口密度 y = 1.630-0.013x <0.001

根据TN浓度空间分布图(图 4)，不难发现TN污染呈现城市高、郊区低的空间分布特征，城区又以靠北的旧城区污染为重.结合所构建的GWR模型结果(图 5)，发现农用地对TN的影响并非如OLS模型(表 2)及Spearman结果所示完全表现为负相关，而显示出明显的局部特征.从回归系数的方向分析，在盆域Ⅰ区，农用地与TN首先表现为正相关，随着河道进入城区，开始变为负相关，在Ⅳ、Ⅴ区北部及Ⅶ区两者又表现为正相关；从回归系数的大小分析，旧城区农用地与TN局部回归系数的绝对值高于其它区域.

图 4(Fig.4)

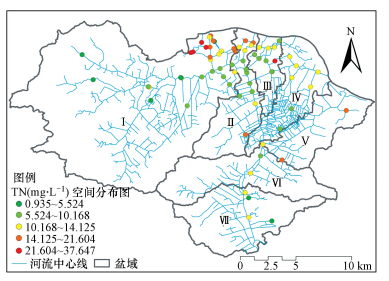图 4 水质指标TN浓度空间分布专题图 Fig.4 Distribution diagram of TN concentration

图 5(Fig.5)

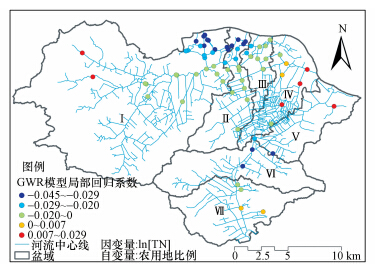图 5 农用地与TN所构建GWR模型之局部回归系数分布图 Fig.5 Distribution diagram of local regression parameters for TN and agricultural l and based on GWR

究其原因，Ⅰ区左侧监测站(瞿溪、郭溪)位处河道上游，水质污染相对较低，TN浓度均值为2.3 mg · L^-1，周边相邻10个子流域内土地利用类型以林地(57.7%)、农用地(20.2%)及住宅用地(6.6%)为主，此处氮含量主要来自畜禽粪便及农药化肥的施用，人为耕作活动对水质起主要影响作用，因而表现出农用地与TN正相关的结果.而在Ⅰ区中部位处郊区的河道，TN浓度均值为7.3 mg · L^-1，周边20个子流域内不透水面积(包括工矿、住宅及商服用地等)占36.9%，其次为农用地34.6%和绿地22.6%；且随着河道步入城区，TN浓度均值达12.1 mg · L^-1，对应测站周边60个子流域内以住宅用地为主，约占26.1%，其次为商服用地和交通用地，总不透水面积比例为73.3%，而农用地和绿地仅分别为6.5%、12.4%，且存在部分子流域内无农用地的现象.这样，随着子流域靠向城区，对应农用地所占比例在 逐渐降低，而其TN浓度却在增加，因此，回归系数 表现为负值.这也是为何OLS模型及Spearman分析结果中农用地与TN整体表现负相关的原因.但是，此时的负相关并不能用来反向表征农用地的增加抑制或降低了TN的污染，而是因为造成河流氮污染的主要污染源随空间位置发生了改变，城区不透水面积迅速增加、点源污染增多是导致TN浓度上升的主要原因；此外，旧城区河道狭窄、流速缓慢且底泥相对较厚，TN浓度迅速升高，从而使得其与农用地的局部回归系数绝对值更大.

而在Ⅳ区北部，TN平均浓度为12.5 mg · L^-1，与城区持平，且进入Ⅴ区有增加趋势，农用地比例与此变化一致，两者呈正相关，但此时快速增加的工矿用地(21.7%)是导致TN浓度上升的主要原因.Ⅵ区测站多设于塘河主河道，水质受上游城区影响显著，TN浓度均值为10.8 mg · L^-1，对应农用地逐渐增加，表现出与TN负相关的结果.Ⅶ区河道自北向南流入瑞安市，上游山脚处水质明显优于河道，周边土地利用变化与瞿溪、郭溪所在Ⅰ区类似，TN受农用地影响显著，两者又表现为正相关关系.

在TN与交通用地所构建的OLS模型(表 2)中，两者回归系数为正值，表明交通用地的增大一定程度上加剧了水质的恶化.而在GWR模型中(图 6)，交通用地对水质的正相关作用表现为城区影响小、郊区及农村影响大的空间变化特征，且东部工业园区(盆域Ⅳ、Ⅴ区北部)出现负相关结果.

图 6(Fig.6)

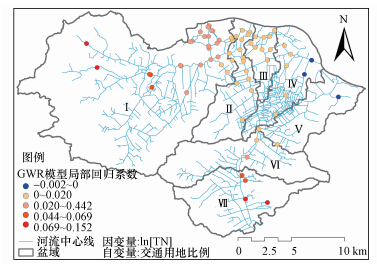图 6 交通用地与TN所构建GWR模型之局部回归系数分布图 Fig.6 Distribution diagram of local regression parameters for TN and transportation l and based on GWR

结合TN浓度空间分布专题图(图 4)分析可知，随着河道由Ⅰ区自西向东进入Ⅱ、Ⅲ、Ⅳ区，并于Ⅶ区自北向南流出，TN浓度及交通用地密度均呈现先增加后减少的变化趋势，因而回归系数为正.而Ⅳ、Ⅴ区东北部，交通用地比例由城区的16.2%降至11.9%，工矿用地则由11.3%增至21.7%，因而在比例变化上交通用地与TN回归系数呈现为负相关，但此处导致TN浓度变化的决定因素并非交通用地而是工矿用地的改变.可见，此时所构建的GWR模型丢失了关键解释变量.如何同时引入多个有效解释变量并同时避免多重共线问题的产生，这是本文今后所需开展的方向.

从局部回归系数的方向分析，由DO与人口密度所构建的GWR模型结果(图 7)在整个研究区域内均表现为负值，与OLS结果(表 2)吻合；从回归系数的大小分析，在GWR模型中人口密度对DO的影响在郊区及农村表现的更为明显.这是因为从农村、郊区再到城市，对应测站平均人口密度由12.8、60.8人· hm^-2增至170.9人· hm^-2，区域间人口密度基数在增加而增涨幅度却在逐步降低，城市区域内人口密度则趋于稳定，因而在局部回归系数上表现为郊区人口密度与DO的回归系数值更大.这与实际情况也是符合的，因为在城区，影响水质的因素复杂而多样，人口因素相对其它指标如城市不透水面积、污染点源等对水质的影响则表现的较弱；而在郊区及农村，水质主要受农用地、住宅用地等人为活动影响，而此两者则与人口密度息息相关.

图 7(Fig.7)

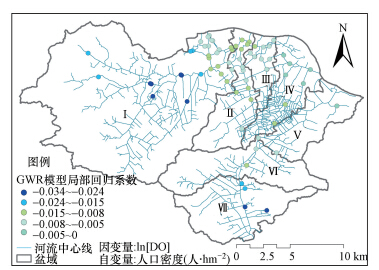图 7 人口密度与DO所构建GWR模型之局部回归系数分布图 Fig.7 Distribution diagram of local regression parameters for DO and population density based on GWR

查阅两模型的校正系数R²、AIC_c及全局Moran′s I计算结果(表 3)可知，相对OLS模型，所有GWR模型的校正R²均得到了较大的提高.以交通用地与不同水质指标所构建的模型为例，其OLS模型校正R²取值范围为0.013~0.243，对应GWR模型中取值为0.159~0.436，平均提升幅度为323.2%.而在以氨氮为因变量的所有模型中，其与水域面积百分比所构建的GWR模型校正R²达0.614，不仅远大于对应OLS模型结果，也高于与其它土地利用类型的R²值，线性模拟能力最好.即使OLS模型中与土地利用类型回归系数均较小的pH指标，其对应的GWR模型的校正R²也得到了提升.

表 3(Table 3)

表 3 GWR与OLS两模型结果对比(校正R2 、AICc及残差Moran′s I) Table 3 Comparison of adjusted R square，AICc and residuals′ Moran′s I from GWR and OLS models

表 3 GWR与OLS两模型结果对比(校正R2 、AICc及残差Moran′s I) Table 3 Comparison of adjusted R square，AICc and residuals′ Moran′s I from GWR and OLS models 参数 DO TN NH+4-N pH EC 校正R2 AICc Moran′s I 校正R2 AICc Moran′s I 校正R2 AICc Moran′s I 校正R2 AICc Moran′s I 校正R2 AICc Moran′s I 注：黑斜体表示所建OLS模型不具有显著性(P>0.05)；黑体表示所求Moran′s I指数不具有显著性(P>0.05) 交通用地比例 OLS 0.243 133.8 0.052 0.13 127.1 0.268 0.136 154 0.178 0.115 -316.2 -0.005 0.013 85.4 0.140 GWR 0.334 128.6 -0.034 0.321 113.9 0.188 0.436 128.7 0.124 0.216 -322.1 -0.043 0.159 76.2 0.128 住宅用地比例 OLS -0.002 153.4 0.123 -0.012 137.7 0.138 -0.010 164.9 0.087 0.072 -312.9 0.048 0.023 84.6 0.085 GWR 0.365 130.4 -0.029 0.378 112.5 0.153 0.468 128.9 0.085 0.232 -322.3 -0.045 0.172 75.7 0.100 农用地比例 OLS 0.103 145.7 0.056 0.069 131.8 0.155 0.067 159.3 0.092 0.034 -310.1 0.074 0.032 84.0 0.119 GWR 0.330 133.3 -0.024 0.319 118.0 0.126 0.418 134.4 0.071 0.194 -319.1 -0.023 0.158 78.9 0.127 商服用地比例 OLS 0.048 149.9 0.090 0.080 131.1 0.183 0.071 159 0.111 -0.006 -307.2 0.089 -0.010 87.0 0.104 GWR 0.350 133.0 -0.017 0.352 116.3 0.159 0.447 132.6 0.083 0.201 -318.9 -0.024 0.217 79.0 0.060 工矿用地比例 OLS 0.007 152.8 0.160 -0.007 137.3 0.133 -0.008 164.8 0.089 -0.013 -306.7 0.109 -0.015 87.3 0.094 GWR 0.318 135.2 0.003 0.289 121.7 0.138 0.395 137.8 0.075 0.205 -320.3 -0.028 0.195 79.9 0.095 绿地比例 OLS 0.057 149.2 0.101 0.045 133.6 0.170 0.056 160.1 0.115 0.086 -314.0 0.019 -0.002 86.4 0.108 GWR 0.379 129.1 0.002 0.376 112.9 0.170 0.477 128.0 0.115 0.187 -319.2 -0.034 0.123 79.7 0.109 水域比例 OLS 0.041 150.4 0.136 0.02 135.4 0.130 0.001 164.1 0.082 0.022 -309.2 0.130 -0.014 87.3 0.093 GWR 0.496 113.6 -0.017 0.56 87.7 0.174 0.614 105.9 0.080 0.249 -325.1 -0.018 0.311 68.5 0.107 人口密度 OLS 0.243 133.8 0.024 0.099 129.6 0.189 0.108 156.2 0.124 0.077 -313.3 0.043 -0.015 87.3 0.097 GWR 0.335 131.8 0.029 0.322 115.2 0.172 0.423 131.5 0.115 0.265 -322.2 -0.064 0.352 63.0 0.061

作为衡量模型精确度和复杂性的重要标准，AIC_c值越低表明模型预测结果与实际结果越接近.由表 3不难发现，除去DO与人口密度所构建的模型外，其余所有GWR模型的AIC_c值都低于对应OLS模型结果，且差值均大于3.在TN与不同土地利用所构建的模型中，AIC_c均值由OLS模型中的133.0降低为GWR模型中的112.3，平均降幅为15.5%.综合上述两种指标的比较，可以判断，GWR作为一种局部统计模型，其模型预测精度优于OLS等传统全局模型，这也验证了Pratt等(2012)及Tu(2013)的研究结果.

然而，针对由残差计算的Moran′s I指数值，对比发现所有OLS及GWR模型的指数值均不具有统计学上的显著性(P>0.05)，这表明回归残差的空间分布很可能是随机空间过程的结果，两模型均不存在明显的预测过度(高残差聚类)和预测不足(低残差聚类)现象.这一点并未表现出Tu等(2008)及Javi等(2014)文中所提出的结论，即GWR相对OLS模型具备更好的处理空间自相关能力.这主要是因为在评比GWR与OLS处理空间自相关能力前，一个假设前提就是初始数据存在某种自相关.然而，通过对本研究中不同水质指标进行空间自相关分析(表 4)发现，研究区域内初始水质监测数据本身就不存在显著的空间聚类模式，自然也无从谈起两模型处理自相关能力的优劣.

表 4(Table 4)

表 4 不同水质指标空间自相关分析结果 Table 4 Spatial autocorrelation analysis of different water quality indicators

表 4 不同水质指标空间自相关分析结果 Table 4 Spatial autocorrelation analysis of different water quality indicators 水质指标 Moran′s I P DO 0.137 0.428 TN 0.140 0.408 NH+4-N 0.090 0.571 pH 0.115 0.407 EC 0.095 0.549

1)土地利用与水质的关系往往随着空间位置的改变表现出局部变化特征.即使在同一研究区域的不同子流域，同一土地利用类型对水质的影响在大小、方向上均可能表现不同.以温瑞塘河流域TN与农用地的关系为例，两者局部回归参数在方向上表现出农村正、城区负的结果，在大小上又以旧城区回归参数的绝对值较高.

2)相邻子流域土地利用百分比的改变及水体污染源的不同，是导致土地利用对水质作用发生变化的根本原因.从土地利用角度分析，在农村地区，农用地比例和TN浓度变化一致，随着河道步入城区，农用地比例减少而TN浓度增加使得两者表现为负相关，在旧城区TN浓度增加迅速从而使负相关性更为显著；从污染源角度分析，农村地区TN含量受农药化肥、牲畜粪便等人类耕作活动影响密切，郊区城区TN含量主要来自皮革工业、城市生活污水等点源污染及大范围的不透水用地等，旧城区TN浓度的迅速增加主要受所处河道狭窄、流速缓慢且底泥相对较厚所致.

3)对比校正R²和AIC_c两个指标发现，所构建的GWR模型预测精度整体优于OLS传统全局模型.根据残差和初始水质数据各自的Moran′s I结果得知，若研究区域不存在明显空间聚类模式，则评比GWR模型与OLS模型处理空间自相关的能力并无意义.