絮凝(凝聚、絮凝)是胶体化学的重要原理之一,它被应用于水质净化成为重要的单元操作之一.通过絮凝可以使水中细小的悬浮颗粒凝并成大的絮体,然后从水中沉降分离.絮凝的化学和絮凝动力学是絮凝科学的两大支柱.其中絮凝动力学研究絮凝的速度问题,只有具有一定速度的絮凝过程才能满足水处理对出水水量的要求,因而才具有实际意义,所以对絮凝动力学的讨论是水处理絮凝学的重要方面.
胶体之所以稳定是由于综合位能曲线上有势垒存在(常青,2011).倘若势垒为零,每次碰撞必导致聚沉,称为快速絮凝; 若势垒不为零,则仅有一部分碰撞会引起聚沉,称为慢速絮凝.无论是对于快速絮凝还是对于慢速絮凝,微粒之间的相互碰撞是首要条件,而它们的相互碰撞是由其相对运动引起的.造成这种相对运动的原因可以是微粒的布朗运动,也可以是产生速度梯度的流体运动.前者称为异向絮凝,后者称为同向絮凝.在异向絮凝中微粒的碰撞频率决定于微粒的热扩散运动.Smoluchowski将扩散理论用于聚沉,得到了球形微粒的聚沉速度(常青,2011).由计算知道,依靠布朗运动的异向絮凝速度太慢,不能单独应用,特别是当微粒相互碰撞聚集变得较大后,布朗运动就会减弱甚至停止,絮凝作用就会减慢甚至不再会发生.但是,长期以来人们观察到,缓慢的搅动会助长絮凝,这是因为搅动会引起液体中速度梯度的形成,从而引起微粒之间的相对运动而造成微粒的相互碰撞,这就是同向絮凝.对具有恒定速度梯度的均匀液体的切变场,可以导出絮凝动力学的同向絮凝的Smoluchowski公式(Smoluchowski,1917; 常青,2011):
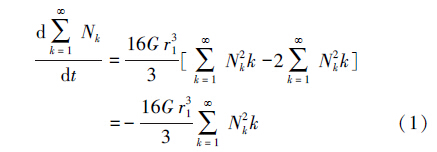
式中,N是微粒的数目浓度(个· m-3),k 的数值指示微粒尺度的大小,t是反应时间(s),G是速度梯度(s-1),r1是初始微粒的半径(m).
然而在实际水处理中,这样的恒定速度梯度是很难找到的,通常被大家所接受的是Camp-Stein的理论(Camp and Stein, 1943; 常青,2011),即以非均匀切变流体耗散在单位体积液体中的功率来计算速度梯度值.
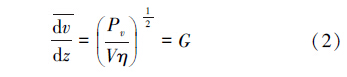
式中,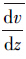 和Pv分别代表池中的平均速度梯度和施加于整个池子中的搅拌功率(W · s-1),V 是反应池的体积(m3),η是流体的粘度(Pa · s).Camp-Stein的上述理论发表后,成了反应池的一个最基本的理论公式,人们假设只要速度梯度值相同混合条件就相同,速度梯度值都通过能量的输入计算得到,并被广泛应用于絮凝设备的设计和放大工作.
和Pv分别代表池中的平均速度梯度和施加于整个池子中的搅拌功率(W · s-1),V 是反应池的体积(m3),η是流体的粘度(Pa · s).Camp-Stein的上述理论发表后,成了反应池的一个最基本的理论公式,人们假设只要速度梯度值相同混合条件就相同,速度梯度值都通过能量的输入计算得到,并被广泛应用于絮凝设备的设计和放大工作.
在工业规模的絮凝反应设备中,流体的流态是以湍流占优势的,并非层流状态,不存在整体和恒定不变的速度梯度,因而将层流条件下得到的Smoluchowski公式或将Camp和Stein提出的计算式代入Smoluchowski层流公式,应用于工业生产是有问题的,因而半个世纪以来,Camp-Stein理论一直受到专家学者的质疑(Cleasby,1984; Han and Lawler, 1992; Park and Park, 2002).以后的研究说明反应设备中实际存在的速度梯度远低于按Camp-Stein理论计算所得的值,特别是近年来发展起来的网格絮凝反应设备的絮凝效果远远超过了其它絮凝设备,但在网格后面一定距离处为均匀各向同性湍流,其速度梯度为零(孙喆和杨基先,1998),更加与速度梯度的理论不相符.实际上在一般情况下,由于湍动涡旋的作用,大大增加了湍流中的动量交换,均化了湍流中的速度分布,所以其速度梯度远小于按Camp-Stein理论计算的结果(Park and Park, 2002).此外,由于在Smoluchowski公式中用能量项替代了速度梯度,所以不能反映湍流中涡和速度梯度的大小、数量及分布等,无法揭示湍流条件下颗粒碰撞的微观本质,不利于絮凝动力学的进一步发展.笔者认为,一定的速度梯度必定需要一定量的能量输入,但一定量的能量输入并不一定对应产生一定的速度梯度,对于速度梯度均匀恒定不变的流动如此,对于湍流情况更是如此.
2 湍流絮凝动力学现状(Current state of flocculation dynamics in turbulent flow)近年来,许多学者曾尝试直接从湍流理论探讨湍流条件下的絮凝动力学,其中较为典型的是Levich的工作.根据Kolmogoroff局部各向同性理论(Kolmogorov,1941a; Casson and Lawler, 1990),湍流是一种不规则的复杂运动,是由各种尺度不同的涡旋叠加而成的流体运动.在湍流条件下搅拌混合输入的能量主要用于一级尺度的大涡旋的形成,一级尺度的涡旋逐级分解为次一级尺度的涡旋,能量通过逐级递减的涡旋进行传递,直到涡旋达到某种尺度时,所有能量会被粘性阻力完全耗散,此时涡旋的尺度被称为Kolmogorov微尺度.Levich认为在这些大小不等的涡旋中,大涡旋往往使颗粒作整体运动而不会使之相互碰撞,尺度过小的涡旋其强度往往不足以推动颗粒碰撞,只有与颗粒尺度相近的涡旋才会引起颗粒间的相互碰撞(Kolmogorov,1941b; Casson and Lawler, 1990),导致絮凝的发生,类似于异向絮凝中布朗运动引起的颗粒碰撞.根据此项假设,应用异向絮凝的碰撞速率公式,并代入脉动流速表示式,得到了各向同性湍流条件下颗粒的碰撞速率如下(Kolmogorov,1941b; American Water Works Association Coagulation Committee,1989):
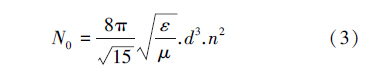
式中,N0是颗粒碰撞速率(次 · s-1),ε是单位时间内单位体积流体的有效能耗(J · m-3 · s-1),也是脉动流速所耗功率,而不是Camp-Stein理论中的单位体积流体所耗总功率,μ是水的运动粘度(m2 · s-1),d是颗粒的直径(m),n是颗粒的粒数浓度(个· m-3),此即微涡旋理论.
该理论仅提出了受水流粘性影响的小涡旋的絮凝作用,类似于布朗运动引起的异相絮凝.事实上,布朗运动是由介质的分子对微粒从各个方向的有限次碰撞不能抵消所引起(根据概率知识,对于无限次碰撞,各个方向的碰撞次数可认为基本相等,因而可以抵消,对于有限次碰撞,各个方向的碰撞次数可认为不相等,因而不能抵消),而介质分子的尺度比这些微粒要小得多,据此小于微粒的涡旋的湍动也应是微粒相互碰撞的推动者.至于体积大于微粒的涡旋对絮凝是否有贡献也无直接证据,所以可以认为该理论尚不完整.此外有效功率ε在实际中也很难确定,因而其局限性是明显的.
3 应用粒子图像速度场仪研究絮凝动力学(Research of flocculation dynamics by particle image velocimetry)对湍流絮凝动力学的研究应该与对湍流的研究密切相关,但湍流是一种极其复杂的流体运动,其运动特征具有很强的随机性,应用复杂的数学求解使得对湍流的研究具有极高的难度,因而至今尚未有一个公认的定义能全面的描述湍流的所有特征,人们对湍流的认识仍然具有很大的局限性.近年来随着技术的进步,实验已不再是验证理论的手段,而成了指导新理论产生的有力工具.20世纪90年代出现的粒子图像速度场仪(Particle Image Velocimetry or PIV)是超出单空间点的测量技术,能在瞬间测出几千乃至上万个点的速度,提供丰富的流动空间结构信息,定量揭示复杂流动和非稳态流动的整体结构(Dantec Dynamics,2002; Park et al., 2002; Wang et al., 2005a; Wang et al., 2005b).PIV仪器由激光器、高速CCD-像机、透镜组、同步器(HUB)、主电脑及PIV软件构成.在激光器发出的片光照射下,事先投入水中的具有跟随性的示踪粒子会产生散射光,用高速CCD-相机即可拍摄到这些示踪粒子,然后PIV软件利用自动关联技术可获得示踪粒子的瞬时位移,基于示踪粒子的跟随性,计算出复杂和非稳态流的局部瞬时速度梯度、涡、整体结构及全场速度场,一方面掌握涡的数量、尺度、旋转角速度、逐级递减速率等,另一方面掌握局部瞬时速度梯度的发生频率、尺度、强度等,寻求湍流涡旋及局部瞬时速度梯度发生和发展的条件及其控制参数.此项技术已被应用于流场的研究(Park and Park, 2002; Wang et al., 2005a; Wang et al., 2005b).近年来光学和计算机技术的进步解决了该仪器储存空间及其CCD-照相机频率的问题,大大提高了它的能力,使之应用于絮凝的研究成为可能.由于PIV是一种非介入型的光学测量装置,具有图像处理软件包,除了获取流场信息外还可以在不破坏絮体的条件下连续地在毫秒内捕获絮体的原位图像,并利用其图像分析技术求出其等当直径和分形维数.
初期应用PIV研究絮凝动力学主要是测量颗粒和絮体的粒径在絮凝过程中的分布及变化情况(Coufort et al., 2005; Kilander et al., 2006; Kilander et al., 2007; Xiao et al., 2011).研究者曾经将烧杯实验或Taylor-Couette反应器中颗粒和絮体的粒径分布及其变化记录下来,应用絮凝-剪切破碎-重新絮凝的程序研究絮体的形成、絮体破碎后的恢复、絮体尺度和絮体的强度的变化、絮体的形貌和密实程度的变化等,并应用计算流体力学(CFD)通过数值模拟得到湍动动能的粘性耗散率和Kolmogorov微尺度等水力学参数,以此对絮体粒径的变化给以表征和说明(Coufort et al., 2005; Xiao et al., 2011).研究表明,絮体的最可几尺度是最可几湍动动能粘性耗散率εpeak的函数; 在絮体剪切破碎和再絮凝阶段所形成的絮体的尺度表现出与流体的最可几Kolmogorov微尺度有关.在絮凝剂加入后经絮凝实验步骤形成的絮体尺度较大,分形特征较显著,但在絮体剪切破碎后经絮凝步骤形成的絮体的尺度较小,分形结构较弱.
近年来用PIV研究流场结构与絮凝效果之间关系的研究有了进展.PIV 首先被应用于研究固体球形颗粒、乳胶球形微粒形成的絮体及海藻聚集体在水中沉降的流场(Xiao et al., 2007).研究者利用PIV 粒子示踪技术直接观察并记录了上述沉降物体周围示踪粒子的的轨迹,描画出沉降物体周围的流线,为穿过絮体和海藻聚集体内部的液体流动提供了直接的实验证据.研究证明,海藻聚集体似乎更加多孔,分形特征更加显著,流线更易穿过它们内部,大大加强了颗粒的碰撞絮凝及物质向聚集体内部的传输.
毛玉红、常青等(毛玉红等,2012; Mao et al., 2013; 毛玉红等,2014a; 毛玉红等,2014b)用PIV测定了Taylor-Couette反应器的流场特征、絮体形貌,并将此特征与其混凝效能相联系,从而揭示了亚微涡旋的混凝机理.Taylor-Couette装置由两个同心转筒构成,两筒间隙约为10~15 mm,其中内筒旋转,外筒固定,两筒间隙中的液体在内筒的驱动下发生流动.当内筒旋转的角速度从零开始增加至一定值时,流动的不稳定性即开始发生,并经历一系列的流态转变,先后出现层流泰勒涡(TVF)、波状涡(WVF)、调制波状涡(MWVF)和湍流泰勒涡(TTVF)等(Kataoka,1985; Mu-Kweon and Chongyoup, 1997; Wang et al., 2005a; Wang et al., 2005b; Soos et al., 2007),这些涡的尺度与环隙的宽度近似,属于亚微涡旋.由于实际湍流的极端复杂性和不可重复性,人们在实验室研究湍流絮凝机理几乎是不可能的,但利用Taylor-Couette装置可生成稳定的可重复获得的涡旋,这就为研究湍流涡旋的絮凝作用机理提供了可能.图 1即是所测得的内外筒环隙子午面在不同简化雷诺数比下的瞬时平均速度矢量场,图中n为内筒转速(r · min-1),R为简化雷诺数比; 图 2是对应的絮凝效果; 图 3是以PAC为絮凝剂,在不同旋转速度下反应9 min,测得的絮体图像.
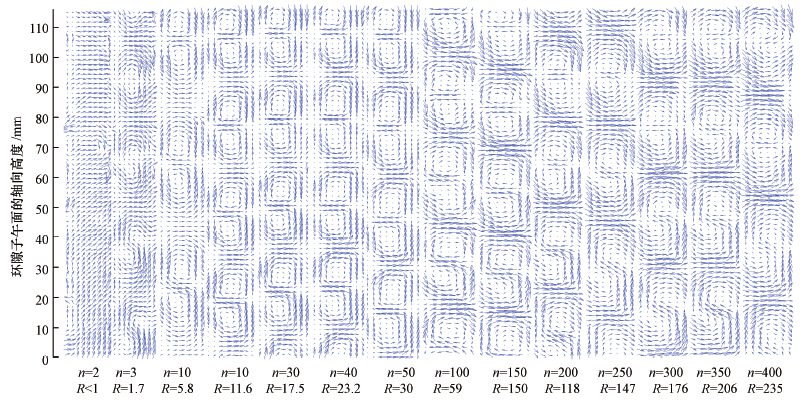 |
| 图 1 用PIV得到的环隙子午面瞬时平均速度矢量场 Fig. 1 Instantaneous and mean velocity vector map of annulus gap meridional plane obtained by PIV (Scale shows the height of meridian plane in axial direction) |
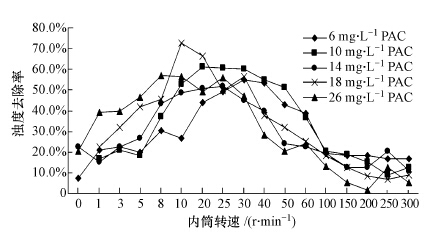 |
| 图 2 不同内筒转速下的絮凝效果 Fig. 2 Flocculation efficiencies of different rotating rates |
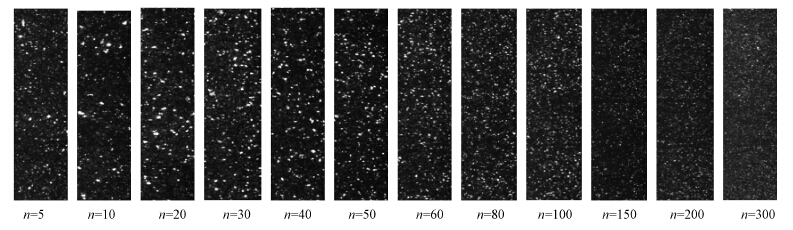 |
| 图 3 各转速下絮体的形貌观测结果 (PAC为絮凝剂) Fig. 3 images of microflocs at different velocity field (The flocculant is PAC) |
图 1表明在环隙子午面上有沿轴向规则分布的漩涡,在很低的转速下,当n=3时系统就表现出了不稳定性.随着转速的升高,环隙中涡旋的数目先是增多,后是减少.涡旋的形态也随着转速的升高从左到右逐渐发生着变化.当n=3~10时仅存在少量非闭合和相互连通的初期涡旋,表明涡旋正在开始形成.当n大于20时形成了许多孤立的,闭合的,完整的和相互分离的涡旋.但随着转速的继续升高,涡旋的完整性和闭合性逐渐降低,相邻涡旋相互连通,n大于50后成为非闭合或敞开式涡旋.图 2表明,反应器中浊度去除率均随着转速的升高先升高后降低,而且几乎在每一种投药量下均在20 r · min-1 至 50 r · min-1即R约处于11.6~30的范围内达到最高值.图 3表明,混凝过程中的颗粒总数相应由多到少,再变多,絮体粒径也相应由小到大,再变小,在20 r · min-1 至 50 r · min-1内絮体体积最大,数目最少.
对照图 1、图 2和图 3可以看出最佳絮凝效果出现在R=11.6~30的范围,其流动机制恰属于波状涡流动(WVF)和调制波状涡流动(MWVF).处于该范围的所有涡漩都是闭合涡,可以认为这种闭合涡有利于涡内颗粒的相互碰撞,为颗粒的相互碰撞提供了良好的场所.研究发现(Wang et al., 2005b; 毛玉红等,2012)在波状涡流动(WVF)范围内涡的体积随着时间发生周期性膨胀和收缩,涡的中心位置也随时间发生径向和轴向振动.所以可以推论涡旋的膨胀收缩会周期性增大或减小了涡内颗粒的运动速度,甚至改变其运动方向,造成局部瞬时速度梯度增大,引起颗粒之间更频繁的相互碰撞,导致较高的混凝效率.随着内筒转速的升高,流动机制由WVF和MWVF开始转变为湍流泰勒涡TTVF,涡旋的膨胀和收缩消失,涡旋的完整性也降低,相邻涡旋相互连通,最终成为非闭合或敞开的涡旋.可以推论,在这种情况下,涡旋中的颗粒可以随水流从一个涡旋流向另一个涡旋,碰撞的几率降低,导致较低的混凝效率.与此相同的是当R小于WVF的R值时,速度梯度很低,初始涡旋正在形成,其形态也是非闭合或敞开式涡旋,同样的原因导致了较低的混凝效率.
以上初步研究表明湍动动能的粘性耗散、涡的性状及大小对絮凝速度有显著的影响,阐明了亚微涡旋的絮凝作用机理,显示了应用粒子图像速度场仪研究湍流絮凝动力学具有良好的应用前景和潜力,有望揭示出前所未知的湍流絮凝的规律.
4 应用计算流体力学研究湍流絮凝动力学(Research of flocculation dynamics by CFD)计算流体力学(Computational Fluid Dynamics,CFD)是利用数值计算和借助计算机求解流体力学方程,对实际设备中流场进行数值模拟的方法,具有精度高、耗时短、费用低,无需实验测量,可提供整个流场内的有关数据等特点(陈卫等,2008).
FLUENT是目前比较流行的计算流体软件,在美国的市场占有率达60%,也是我国目前比较流行的计算流体软件.运用FLUENT数值模拟某个流场,包括建立模型、网格划分、设定边界条件、选择控制方程、选择计算方法、设定材料属性和求解等.常见FLUENT基本构件及其功能如下(朱红钧等,2010)
(1)GAMBIT—FLUENT自带的网格生成软件;
(2)FLUENT求解器—FLUENT核心软件,计算方法、物理模型、边界条件、材料属性等均可在此设置,所有数值运算都在此进行,并提供压力、温度、速度、紊动等各种流场信息.
数值模拟的准确度取决于:①网格划分密度,②边界条件设置,③计算方法是否符合实际情况.在实际数值模拟计算中,网格划分水平的高低直接影响数值模拟计算的运算量与准确度.除了保证网格几何品质,还得考虑网格密度的影响.在不同网格密度下考查数值模拟结果的差异,只有当两种密度下的模拟结果相差很小时为止,这就是所谓的网格独立性(Grid independency)检验,又叫做网格无关性检验、网格敏感性测试(韩占忠等,2004).网格数太密或者太疏都可能产生误差较大的计算结果,只有适度的网格密度下的计算结果才与真实值比较接近.
目前应用CFD研究各种流体流动的报道较多,但研究絮凝反应器中流场的报道尚不多见.韩晓婷、常青等人应用CFD方法对Taylor-Couette反应器的流场做出了数值模拟(韩晓婷等,2013)用以解释反应器中的絮凝效果.如图 4~5所示,其中图 4是速度矢量图,图 5是湍动动能图.图中用不同的颜色表示计算数值的大小,红色表示最大值,深蓝色表示最小值,n表示内筒转速(r · min-1).
 |
| 图 4 以数值模拟得到的子午面速度矢量图 Fig. 4 Velocity vector map of meridian plane obtained by numerical simulation |
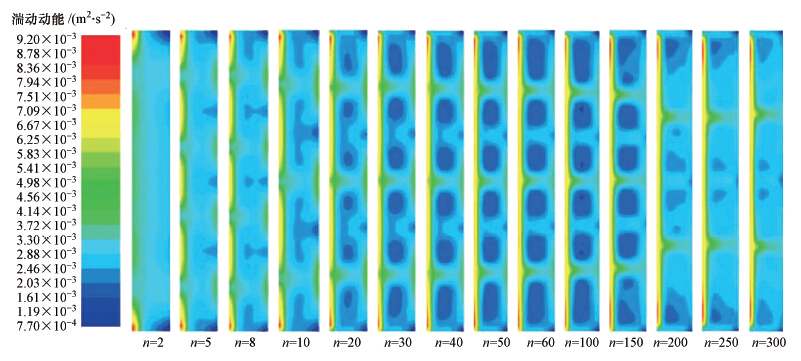 |
| 图 5 以数值模拟得到的子午面湍动动能图 Fig. 5 Contours of turbulent kinetic energy of meridian plane obtained by numerical simulation |
由图 4可知,当内筒转速n=2 r · min-1时流体流线平稳,沿径向无分速度,未出现排列整齐的涡胞结构,但在流场底部存在着由于边壁效应而产生的微小涡旋; n>2 r · min-1后流体表现出不稳定性,内外筒环隙间逐渐出现亚微尺度的涡旋,这些涡旋排列整齐,涡旋数量随转速增大先增多后减少,在n=20~50 r · min-1之间涡旋结构最为清晰,此时形成的涡旋相互分离,相对孤立,闭合且完整,如PIV部分所述,这种涡旋有利于絮体的形成; 继续增加转速后这种闭合完整性降低,相邻涡旋相互连通.由图 4还可以看出,代表速度较大的红、黄色区域主要分布在内筒边壁和涡旋之间,代表速度较小的蓝色区域主要分布在涡旋内部,说明涡旋内部速度较小,内外边壁附以及涡旋之间速度较大,这种速度分布也有利于絮体形成.
由图 5可知,代表湍动动能较大的红色、黄色区域主要分布在反应器内筒边壁和相邻涡旋之间,代表湍动动能较小的深蓝色区域则分布在反应器上下底面和涡旋内部,说明边壁附近湍动动能大,涡旋内部湍动动能小.随内筒转速增大,湍动动能的分布与速度矢量分布相似,呈现一定的规律性.涡旋的湍流运动是絮体颗粒发生接触碰撞的主要原因,低转速下,当n<20 r · min-1时湍动能较小,不足以使絮体颗粒发生有效碰撞,致使絮凝效率较低.当转速增加,湍动能相应增加,涡旋的膨胀和收缩加剧,促使絮体颗粒相互碰撞的几率增大,促进了絮凝效果.当转速继续增大,n>50 r · min-1时,过大的湍动动能会导致过大的湍流剪切力,破坏絮体间的吸附架桥作用(栾兆坤,2001),使絮体破碎成细小颗粒,密实度降低,不易沉降,严重影响了絮凝效果.因此如能将湍动动能有效地控制在适宜范围内,就能保证较好的絮凝效果.
近年来,CFD数值模拟技术已逐渐被应用于实际絮凝设备的研究,例如基于FLUENT 技术以流场速度分布、紊动动能、有效能耗作为评价标准,对不同板长和夹角的异波折板絮凝反应器的流场进行了数值模拟(曾立云等,2011).图 6是夹角分别为90°、120°的情况下,板长分别为30 cm、40 cm、50 cm的反应器的速度云图(曾立云等,2011).
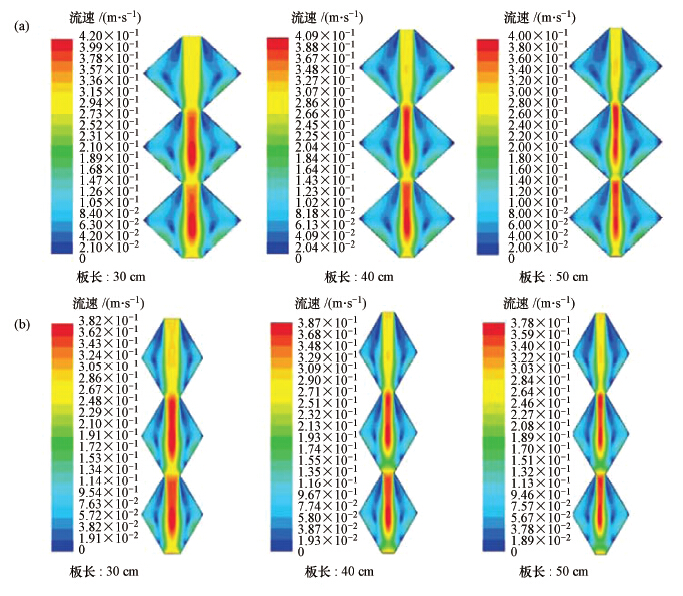 |
| 图 6 以数值模拟得到的异波折板反应器的速度云图 (a.夹角90°; b.夹角120°) Fig. 6 Contours of velocity of asynchronous folded plate reactors obtained by numerical simulation (a. Angle of 90°; b. Angle of 120°) |
其中a图的折板夹角为90°,b图的折板夹角为120°.速度的相对大小均以颜色差表示.与夹角120°的长折板反应器云图的比较表明,夹角90°的短折板适宜于絮凝前段,而夹角120°的长折板更适宜于后续絮凝段.在此基础上建议对絮凝前段的折板单元进行结构优化,在每个折板单元中心增设菱形扰流板,用以增强折板内流场紊动动能,提高有效能耗相对比例.
CFD的应用表明速度矢量、湍动动能、有效能耗等对絮体性状、絮体尺度及絮凝效果有显著的影响,改进反应器的设计可改变它们的强度和分布,有效改善絮凝效果,与PIV技术相互印证,相互补充,有可能为进一步揭示湍流絮凝的致因做出贡献.
5 结论(Conclusions)Smoluchowski理论认为在均匀切变场中即层流条件下,絮凝速度与流场的速度梯度成正比; 对于速度梯度并非均匀恒定不变的流动或湍流情况,Camp-Stein提出速度梯度可以通过流体耗散在单位体积液体中的功率进行计算,但这一做法尚存在较大的局限性和误差; 对于湍流情况,微涡旋理论认为,只有尺度与颗粒相近的涡旋才会推动颗粒的相互碰撞,导致絮凝发生,但这一理论并未涉及其他尺度涡旋的作用.近年来出现的粒子图像速度场仪及计算流体力学为研究湍流絮凝提供了新的手段,初步说明了涡的形态及大小、速度矢量、湍动动能、有效能耗等对絮凝速度、絮体性状、絮体尺度的影响,分析了其机理.该两种方法的应用和结合显示了良好的应用前景,有可能为进一步揭示湍流絮凝的致因做出贡献.
| [1] | American Water Works Association Coagulation Committee. 1989. Committee report:Coagulation as an integrated water treatment process[J]. Journal-American Water Works Association, 81(10):72-78 |
| [2] | Camp T R, Stein P C. 1943. Velocity gradients and internal work in fluid motion[J]. Journal of the Boston Society of Civil Engineers, 30:219-237 |
| [3] | Casson L W, Lawler D F. 1990. Flocculation in turbulent flow:Measurement and modeling of particle size distributions[J]. Journal-American Water Works Association, 82(8):54-68 |
| [4] | 常青. 2011. 水处理絮凝学(第2版)[M]. 北京:化学工业出版社. 27-29; 30-35 |
| [5] | 陈卫, 邹琳, 王德爟. 2008. 水处理絮凝动力学及其效果的数值模拟[J]. 解放军理工大学学报(自然科学版), 9(3):279-285 |
| [6] | Cleasby J L. 1984. Is velocity gradient a valid turbulent flocculation parameter?[J]. Journal of Environmental Engineering, 110(5):875-897 |
| [7] | Coufort C, Bouyer D, Liné A. 2005. Flocculation related to local hydrodynamics in a Taylor-Couette reactor and in a jar[J]. Chemical Engineering Science, 60(8/9):2179-2192 |
| [8] | Dantec Dynamics. 2002. FlowMap 3D-PIV System (Fifth edition)[R]. Dantec Dynamics A/S, Denmark |
| [9] | Han M, Lawler D F. 1992. The (relative) insignificance of G value in flocculation[J]. Journal-American Water Works Association, 84(10):79-91 |
| [10] | 韩晓婷, 常青, 毛玉红, 等. 2013. Taylor-Couette流场数值模拟及絮凝效果研究[J]. 环境科学学报, 33(6):1637-1641 |
| [11] | 韩占忠, 王敬, 兰小平. 2004. FLUENT-流体工程仿真计算实例与应用[M]. 北京:北京理工大学出版社 |
| [12] | Kataoka K.1985. Encyclopedia of fluid mechanics,in Taylor vortices and instabilities in circular couette flows[M].vol. 1. New York:Housing Gulf Publishing. 237-273 |
| [13] | Kilander J, Blomstr m S, Rasmuson A. 2006. Spatial and temporal evolution of floc size distribution in a stirred square tank investigated using PIV and image analysis[J]. Chemical Engineering Science, 61(23):7651-7667 |
| [14] | Kilander J, Blomstr m S, Rasmuson A. 2007. Scale-up behaviour in stirred square flocculation tanks[J]. Chemical Engineering Science, 62(6):1606-1618 |
| [15] | Kolmogorov A N. 1941a. Dissipation of energy in the locally isotropic turbulence[C]./Proceedings of the USSR Academy of Sciences, 32:16-18 (in Russian). |
| [16] | Kolmogorov A N. 1941b. The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers[C]. Proceedings of the USSR Academy of Sciences 30:299-303 (in Russian). |
| [17] | Mao Y H, Chang Q, Zeng L Y, et al. 2013. Velocity field structure and flocculation efficiency in Taylor-Couette flow[J]. Separation Science and Technology, 48(4):659-663 |
| [18] | 毛玉红, 常青, 曾立云, 等. 2012. 亚微涡旋的混凝作用研究[J]. 中国环境科学, 32(3):467-472 |
| [19] | 毛玉红, 常青, 曾立云. 2014a. 混凝过程中絮体形貌的PIV 成像观测与表征[J]. 中国环境科学, 34(4):951-957 |
| [20] | 毛玉红, 常青, 曾立云. 2014b. 混凝过程中流场结构的PIV 测量与表征[J]. 环境科学学报, 34(5):1206-1211 |
| [21] | Mu-Kweon Y, Chongyoup K. 1997. Experimental studies on the Taylor instability of dilute polymer solutions[J]. Journal of Non-Newtonian Fluid Mechanics, 72(2/3):113-139 |
| [22] | Park N-S, Park H. 2002. Analysis of local velocity gradients in rapid mixer using particle image velocimetry Technique[J]. Water Science and Technology:Water Supply, 2 (5/6):47-55 |
| [23] | Smoluchowski M. 1917. Versuch einer mathematischen Theorie der Koagulationskinetik kolloider L sungen[J]. Zeitschrift für Physikalische Chemie, 92:129-168 |
| [24] | Soos M, Wang L, Fox R O, et al. 2007. Population balance modeling of aggregation and breakage in turbulent Taylor-Couette flow[J]. Journal of Colloid and Interface Science, 307(2):433-446 |
| [25] | 孙喆, 杨基先. 1998. 旋流-网格混凝设备处理低温低浊水的试验研究[J]. 中国给水排水, 14(2):32-34 |
| [26] | Wang L G, Dennis V R, Fox R O. 2005a. CFD simulation of shear-induced aggregation and breakage in turbulent Taylor-Couette flow[J]. Journal of Colloid and Interface Science, 285(1):167-178 |
| [27] | Wang L G, Olsen M G, Vigil R D. 2005b. Reappearance of azimuthal waves in turbulent Taylor-Couette flow at large aspect ratio[J]. Chemical Engineering Science, 60(20):5555-5568 |
| [28] | Xiao F, Li X Y, Lam K M. 2007. Investigation of the hydrodynamic behaviour of particle and aggregates by particle image velocimetry (PIV)[J]. Water Science and Technology:Water Supply, 7(2):213-220 |
| [29] | Xiao F, Lam K M, Li X Y, et al. 2011. PIV characterisation of flocculation dynamics and floc structure in water treatment[J]. Colloids and Surfaces A:Physicochemical and Engineering Aspects, 379(1/3):27-35 |
| [30] | 曾立云, 余昌全, 常青. 2011. 异波折板流场模拟分析与结构优化[J]. 环境科学学报, 31(12):2634-2641 |
| [31] | 朱红钧, 林元华, 谢龙汉. 2010. FLUENT流体分析及仿真实用教程[M]. 北京:人民邮电出版社 |
| [32] | 栾兆坤. 2001. 混凝基础理论研究进展与发展趋势[J]. 环境科学学报, 21(增刊):1-9 |
 2015, Vol. 35
2015, Vol. 35


