城市地表径流是仅次于农业污染源的第二大面污染源(Deletic et al., 1998),其中含有的污染物包括悬浮物、重金属、氯化物、石油类、多环芳烃等.城市地表径流排放产生的短期冲击负荷对于受纳水体的水质会产生短期的不利影响,如果这种冲击负荷发生频率较高,将会对受纳水体的水质产生长期性的影响,进而对整个流域或区域的环境产生负面作用(Tsihrintzis et al., 1997).城市地表径流中污染物浓度的高低受到多种因素的影响,如降雨模式、降雨量、雨强、前期晴天天数、交通量、土地利用类型等(Chui et al., 1982; 李怀恩等,2012; 韩景超等,2013).此外,大气清洗过程、冲刷与侵蚀过程、污染物沉降过程及搬运与输移过程也会影响到城市地表径流中污染物浓度的高低.在城市地表径流含有的众多污染物中,总悬浮固体(Total Suspended Solid,TSS)被认为是其他污染物的主要载体(Chebbo et al., 1992; Jack et al., 1996),地表径流中许多污染物的分布特征与地表径流中颗粒物的分布存在一定的相关性(Furumai et al., 2002; Kim et al., 2007).掌握城市地表径流TSS的排放规律,对于评估受纳城市地表径流的水体的水质状况是极为必要的.由于影响地表径流中污染物浓度高低的因素和过程众多,且影响发生的行为过程复杂,因此,在评估城市地表径流污染及其控制策略和方法的研究中,数学模型是一种常用的方法和有效的手段(Tsihrintzis et al.,1997).
目前,最常用的城市地表径流数学模型是由Sartor和Boyd于1974年提出的一种渐近的指数型冲刷模型(Sartor-Boyd冲刷模型)(Sartor et al., 1974).SWMM(Storm Water Management Mdoel)和HSPF(Hydrologic Simulation Program-FORTRAN)均基于此模型构建(Bicknell et al., 1997;Tsihrintzis et al., 1998).Sartor-Boyd冲刷模型用以描述累计径流量随径流时间单调递增,径流过程排放的污染物浓度随径流时间单调递减这一地表径流排污规律(Millar,1999),但该模型仅适用于具有初期冲刷效应的降雨过程(赵剑强,2002; Whipple et al., 1977);此外,在描述城市区域的地表冲刷过程时还可以采用标定曲线模型(Rating Curve Model)这一简单的概念型模型(US Army Corps of Engineers,1977).标定曲线模型中城市地表污染物的冲刷排放量与地表径流深度(Barrett et al., 1998)或径流量(Imteaz et al., 2014)的指数相关,而地表径流中污染物的浓度变化与地表污染物的累积量无关.该模型无法描述降雨初期和后期由于地表沉积的污染物量变化引起的地表径流中污染物浓度变化,特别是当降雨初期与降雨后期雨强相同时,模型给出的污染物浓度也相同,这与实际情况存在较大差异.近年来,随着数学模型研究的深入,定量化的模型也见诸报道(Deletic et al., 1991;Deletic et al., 2000).但定量化模型由于参数难以获取,此类模型的实际应用也因此受到一定的限制(Crobeddu et al., 2011).目前,仍然缺乏一个能够对径流过程中污染物的排放规律进行准确描述的具有广泛适用性的城市地表径流污染物浓度数学模型.
基于此,本研究提出一个以地表沉积物量(P)与降雨强度(r)的比值(P/r)为主要参数描述地表径流中TSS随径流过程变化的P/r模型.基于发生在陕西省西安市的3场降雨事件的实测数据,采用优化法确定模型的参数取值,并通过与最常用的Sartor-Boyd冲刷模型的预测结果进行比较,研究本文建立的P/r模型的适用性.最后,通过对P/r模型进行不确定性分析,研究将该模型应用于陕西省西安市时模型参数的取值范围及模型预测值对实测值的覆盖度.
2 Sartor-Boyd冲刷模型(Sartor-Boyd wash-off model)Sartor-Boyd冲刷模型是基于“污染物质在晴天时积累于地表,在随后的降雨径流过程中,一部分被冲刷进入排水系统”的概念建立的.累积过程取决于土地使用类型、气象条件、交通状况等因素,冲刷过程则取决于降雨强度、地表的剪切应力等因素.Sartor-Boyd冲刷模型假定径流过程中不透水地面表层沉积物的冲刷速率与地表沉积的污染物量(P)及降雨强度(r)成正比,具体如式(1)所示.
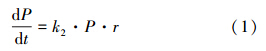
对式(1)积分,可得到t时刻因降雨径流冲刷而排放的污染物量P(t):
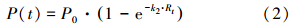
式(1)和式(2)表明,在降雨径流过程中,降雨冲刷排污速率和径流中的污染物浓度随累积径流量呈指数降低.假设集雨面积为A(m2),则地表径流形成后t时刻地表径流中的污染物浓度C(t)可由P(t)对Rt求导获得:
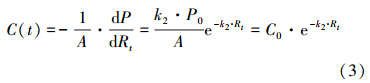
P/r模型的建立基于以下假设:①空气质量、城市地表卫生状况及降雨间隔时间等与地表径流中污染物来源有关的所有因素由地表污染物累积量(P)反映;②地表径流量用集雨面积(A)与降雨强度(r)的乘积表示,即降雨强度等于径流深度;③径流过程中污染物浓度的变化主要和P与r的相对量有关,在P/r模型中采用P/A与r的比值来描述,即单位面积的污染物累积量与单位面积的径流量的比值描述其相对强度.
根据以上假设,并考虑到单位雨强或径流深度下,地表径流中的污染物浓度和径流的冲刷能力可能存在一个上限值;同时,径流中的污染物浓度的变化又会受到地表上沉积的污染物量和降雨强度的影响.基于对这一过程进行的量纲分析,径流产生后t时刻对应的污染物浓度C(t)由式(4)计算.
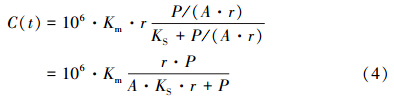
单位时间污染物排放速率由式(4)与地表径流量(A·r)的乘积表示,则:
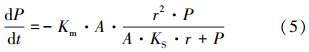
当以地表径流量(q)为变量时,式(4)和(5)也可分别改写为式(6)和(7):
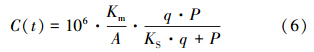
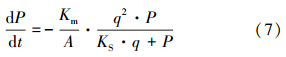
P/r模型存在P/(A·r)>>KS和P/(A·r)<< KS两种特殊情况.当P/(A·r)>>KS时,在这种情况下,降雨初期地表积累的污染物量很大,或者降雨强度很小.式(4)和(5)可近似为:
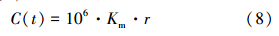
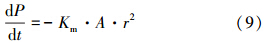
当P/(A·r)<<KS时,在这种情况下,降雨后期地表污染物量很少,或者降雨强度很大,式(4)和(5)可近似为:
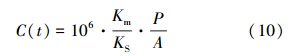
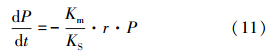
模型参数估计采用优化法.降雨事件中,基于实测的不同降雨径流时刻t对应的径流深度r及地表径流中的污染物浓度C(t),分别采用P/r模型和Sartor-Boyd冲刷模型对降雨过程的实测数据进行拟合,以拟合优度最佳为目标,估计两模型中的参数.
3场降雨数据采集于西安市南二环太白路立交桥的落水管处,采样时间分别为2010年9月3日、2010年9月28日和2010年10月10日,分别为中雨、小雨和大雨(陈莹等,2012).陕西省西安市南二环道路是西安市的一条主要交通干线,专供机动车行驶.样品采集路段为单向3车道沥青混凝土桥面,车流量约为30000辆 · d-1,该路段除正常的道路清扫作业外,无其他人为排污过程影响.降雨事件特征及采样点概况见表 1.考虑到降雨事件存在的时空差异性,本研究所采用的3场降雨事件的地表径流污染物监测数据可认为其基本代表了陕西省西安市秋季降雨过程大交通量路段地表径流的污染物排放规律.
| 表 1 三场降雨事件的特征及采样点概况 Table 1 Characteristics of three rainfall events and general situations of the data-collecting points |
P/r模型中参数Km、KS和P0的估计及验证过程如下:①初步确定Km、KS和P0的合理取值区间;②根据实测的r(i)值,采用式(12)计算径流开始后采样时刻i对应的径流中的污染物浓度;③由式(13)计算径流开始后第(i+1)采样时刻地表残留的污染物量;④以均方根误差(RMSE)为判定条件,在各参数的取值范围内,选取使模型计算浓度值(Ci)与实测值(Oi)的RMSE达到最小时的各参数的数值作为P/r模型的参数值.
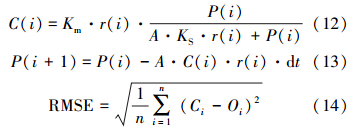
为了评估本研究建立的P/r模型的有效性,本研究对比了P/r模型和Sartor-Boyd冲刷模型对发生在陕西省西安市的3场降雨事件的模拟结果,并采用归一化目标函数(NOF)、相关系数(CC)和相关指数(R2)等统计学指标对两模型的模拟结果进行了分析,通过与Sartor-Boyd冲刷模型预测结果的比较说明本研究建立的P/r模型的适用性.NOF、CC和R2的计算见式(15)~(17).理想的NOF值应为0,但在实际使用过程中,NOF值在0~1之间是可接受的.CC的取值范围为[-1,1],R2的取值范围为[0,1].CC的数值越靠近1,说明正相关性越强.R2的数值越靠近1,表明观测值与预测值之间的拟合程度越强.最后,以Nash-Sutcliffe效率系数(NSE)(Nash et al., 1970)为判别条件,基于3场降雨的实测数据对P/r模型进行不确定性分析,确定了将P/r模型应用于陕西省西安市时模型参数的取值范围及模型预测值对实测值的覆盖度.NSE的计算见式(18).
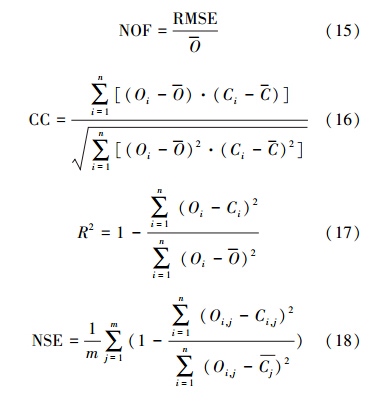
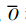 和
和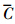 分别为观测值和模型预测值的平均值;Oi,j为第j场降雨在i时刻的实测值;Ci,j为第j场降雨在i时刻的预测值;
分别为观测值和模型预测值的平均值;Oi,j为第j场降雨在i时刻的实测值;Ci,j为第j场降雨在i时刻的预测值;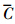 j 为第j场降雨污染物浓度的平均值.
4 结果与讨论(Results and discussion)
4.1 P/r模型和Sartor-Boyd冲刷模型参数的确定
j 为第j场降雨污染物浓度的平均值.
4 结果与讨论(Results and discussion)
4.1 P/r模型和Sartor-Boyd冲刷模型参数的确定 基于3场降雨事件的实测数据,P/r模型和Sartor-Boyd冲刷模型的最佳参数估计见表 2.P/r模型与Sartor-Boyd冲刷模型的模型预测值与降雨过程实测值的统计学计算结果见表 3.
| 表 2 P/r模型和Sartor-Boyd冲刷模型的最佳参数估计 Table 2 Optimal estimations of parameters in the P/r model and the Sartor-Boyd wash-off model |
| 表 3 P/r模型和Sartor-Boyd冲刷模型预测值与实测值的统计学结果 Table 3 Statistics results of simulations and observations of the P/r model and the Sartor-Boyd wash-off model |
在Sartor-Boyd冲刷模型中,冲刷系数k2是一个经验参数,没有明确的物理意义.与Sartor-Boyd冲刷模型相比,P/r模型中的参数变为Km和KS,是两个相互独立且具有明确意义的参数.虽然从量纲的角度来说,Km/Ks与k2相同,但Sartor-Boyd冲刷模型中k2是经验值,无具体的物理意义,与Km/Ks还是有着本质的区别,这也可以从Km/Ks与k2在数值上相差较大看出(表 2).Sartor-Boyd冲刷模型中的参数k2实质上可能并不应该被认为是一个独立的参数.一般情况下,Km/Ks的比值应不等于k2,如表 2所示,但从量纲的角度来看,Km/Ks的含义等同于Sartor-Boyd冲刷模型中的k2,Km/KS与k2之间可能存在某种联系,不排除在某些特定情况下(如降雨强度很大的情况),可能会出现Km/Ks与k2在数值上相等的情况.
从P/r模型和Sartor-Boyd冲刷模型预测值与实测值的统计学结果来看,P/r模型的统计量RMSE、CC和R2均优于Sartor-Boyd冲刷模型,采用Km和KS这两个能够反映降雨特性的参数代替单参数k2来描述地表沉积物量和地表径流中污染物浓度的变化有助于提高模型预测结果的准确性.本研究建立的P/r模型在明确模型参数物理意义的同时,能够更加深刻地揭示地表径流的排污规律.
4.2 P/r模型与Sartor-Boyd冲刷模型预测结果的对比将采用优化法得到的模型参数分别带入P/r模型和Sartor-Boyd冲刷模型,对3次降雨事件产生的地表径流中的污染物浓度进行模拟.3次降雨事件的降雨强度、模型模拟值和地表径流中污染物浓度的实测值见图 1.
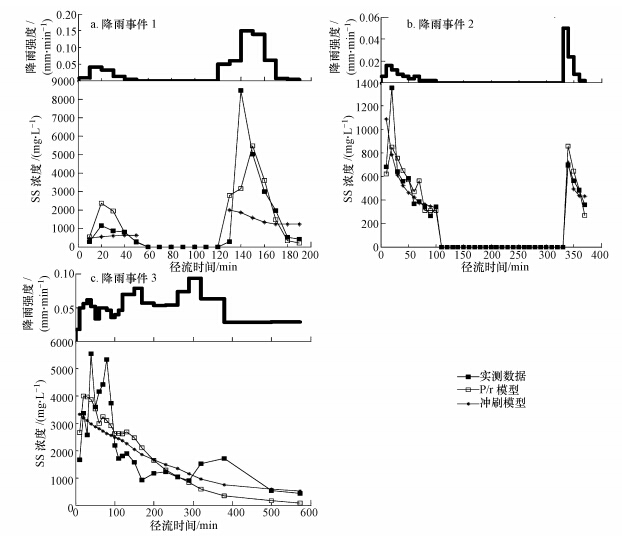 |
| 图 1 P/r模型和Sartor-Boyd冲刷模型的模拟结果与实测值 Fig.1 Simulations and observations of the Sartor-Boyd wash-off model and the P/r model |
3次降雨事件中,降雨事件1和降雨事件2代表了降雨过程中有短暂停歇型的降雨,降雨事件3代表了连续性型降雨.降雨事件1雨强呈先小后大,前期雨强很小且相对均匀,后期雨强较大;降雨事件2雨强呈先小后大,但整场降雨强度均较小;降雨事件3雨强呈先小后大再小的钟形曲线,且不断波动.3次降雨事件中的地表径流的污染物浓度变化过程基本与降雨强度的变化趋势相同.
降雨事件1和降雨事件2中降雨前期径流中的污染物浓度随着降雨强度的增加而增加,随着降雨强度的减小而减小.在降雨后期随着雨强的突然增大,地表径流中的污染物浓度急剧增大,而后随着降雨强度的突然减小又急剧减小.降雨过程中,当降雨强度为0时,不产生地表径流,地表径流中污染物浓度为0.在降雨事件1和降雨事件2中,降雨过程并不连续,分别经历了约1.2 h和3.5 h的停歇期.在降雨过程再次恢复的过程中,地表径流中的污染物浓度在径流冲刷作用下再次增大.从模型对降雨事件产生的地表径流的污染物排放过程的模拟结果来看,P/r模型很好地模拟了地表径流中污染物浓度随雨强的变化而变化的过程.Sartor-Boyd冲刷模型在模拟降雨事件1时,降雨前期地表径流中污染物浓度呈单调增加,降雨后期地表径流中污染物浓度又呈单调递减,这与实际的地表径流污染物浓度变化过程差别较大.在模拟降雨事件2时,降雨前期和降雨后期地表径流中的污染物浓度均单调递减.相比于对降雨事件1的模拟结果,Sartor-Boyd冲刷模型对降雨事件2的拟合程度较好.这主要与地表径流初期冲刷效应的存在与否及模型的适用范围有关.降雨事件2中地表径流初期冲刷效应强于降雨事件1(陈莹等,2012),而Sartor-Boyd冲刷模型适用于模拟具有初期冲刷效应的降雨过程的地表径流污染物排放过程(赵剑强,2002; Whipple et al.,1977).虽然,Sartor-Boyd冲刷模型对具有中等强度的地表径流初期冲刷效应的降雨事件2的模拟效果较好,但降雨强度的波动对地表径流中污染物浓度的影响在模拟结果中并未得到反映.
降雨事件3中,地表径流的污染物浓度变化也基本与降雨强度的变化过程相同,呈钟形曲线.在降雨前期地表径流中污染物浓度随降雨强度的波动而波动,且由于降雨初期冲刷效应的存在,降雨前期地表径流中的污染物浓度明显高于降雨后期时地表径流中的污染物浓度.从两模型的模拟结果来看,Sartor-Boyd冲刷模型模拟的地表径流中污染物浓度随着降雨事件的延长呈单调递减,降雨强度的波动对地表径流中污染物浓度的影响未得到反映.而本研究建立的P/r模型在降雨前期很好地模拟了由于降雨初期冲刷效应导致的地表径流污染物浓度的增加和地表径流中污染物浓度随降雨强度的波动而波动的现象.降雨后期(地表径流产生约4 h后),随着地表沉积的污染物量的逐渐减少,P/r模型模拟结果的变化趋势与Sartor-Boyd冲刷模型模拟结果的变化趋势一致,呈单调递减.在地表径流产生后的4~5 h这一时间段内,P/r模型的模拟值与实测值基本重合,但随后实测的地表径流中的污染物浓度突然升高,使P/r模型的预测值偏离实际值较多,这可能是由于发生了某一未知的随机事件而导致的.
Sartor-Boyd冲刷模型对具有地表径流初期冲刷效应且降雨强度波动较小的降雨事件的地表径流污染物浓度变化过程的拟合度较好,但不适用于描述具有地表径流初期冲刷效应的降雨事件、间歇性降雨事件及降雨强度波动较大的降雨事件的地表径流污染物浓度变化过程.Aryal(2003)将Sartor-Boyd冲刷模型应用于高速公路路面径流的污染物排放规律时发现,Sartor-Boyd冲刷模型不适用于描述间歇性降雨事件引起的路面径流污染物排放过程.此外,对于悬浮物负荷或污染物浓度有波动的情况也不适用(Aryal et al., 2009).总体而言,通过对比3场降雨事件中地表径流污染物浓度的模型预测值与实测值,P/r模型能够更好地描述城市地表径流中TSS随径流时间的变化(图 1),这一结果从表 3中两模型模拟结果的统计学指标也能得到很好的反映.Sartor-Boyd冲刷模型只适用于描述地表径流排污浓度随累计径流量呈单调递减的降雨径流,而对间歇性降雨事件、不存在径流初期冲刷效应的降雨事件和降雨雨强波动较大的降雨事件则并不适用.相比于Sartor-Boyd冲刷模型,P/r模型能够更准确地描述实际地表径流的携污过程,具有更广泛的适用范围.
4.3 P/r模型的不确定性分析不确定性理论认为,对存在不确定性的事件进行数学模拟时,一条最优的拟合曲线并不能真实反映客观事件本身的规律,科学的模拟应该是确定出一组合理的取值区间,该取值区间对应的模拟结果应该达到可接受的对实测结果的覆盖度和带宽.本研究选择NSE作为标准,取NSE阈值为0.46,得到各参数相应的取值区间为P01(降雨事件1中地表沉积的污染物量)为10.0~15.5 kg;P02(降雨事件2中地表沉积的污染物量)为2.0~2.5 kg;P03(降雨事件3中地表沉积的污染物量)为12.5~16.5 kg; KS为0.65~1.35 kg · min · L-1;Km为0.16~0.22 kg · min · mm-1 · L-1. P/r模型预测值的上下限及实际降雨过程的实测值见图 2.P/r模型的预测带平均相对宽度(ARIL)为1.21,预测带对实测值的覆盖度为67%.
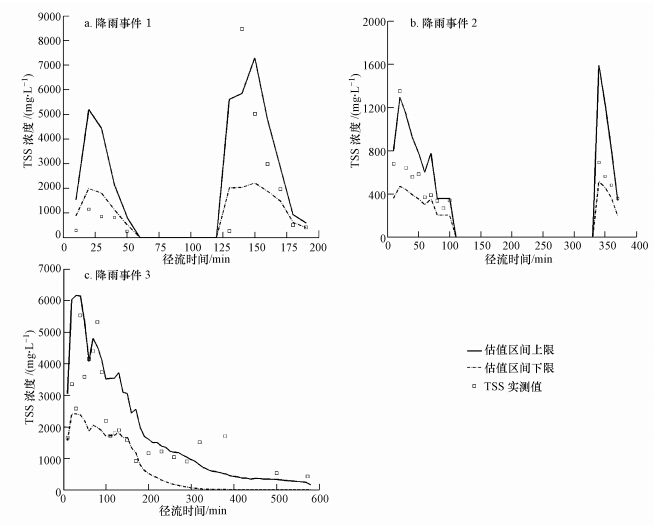 |
| 图 2 P/r模型估值区间与径流TSS浓度实测值值 Fig.2 Estimation range of the P/r model and actual concentration of TSS in runoff |
1)本研究以地表沉积物量与降雨强度的比值为主要参数,构建了一个全新的P/r模型,用以描述降雨过程产生的地表径流中污染物的排放规律.P/r模型采用Km和KS两个参数有助于提高模型预测结果的准确性.P/r模型对降雨事件中地表径流污染物排放过程和规律的描述优于Sartor-Boyd冲刷模型.
2)根据不确定性分析,当Nash-Sutcliffe效率系数取0.46时,采用P/r模型对陕西省西安市地表径流中的污染物浓度进行模拟应采用的KS和Km的取值范围分别为0.65~1.35 kg · min · L-1和0.16~0.22 kg · min · mm-1 · L-1.P/r模型的预测带平均相对宽度(ARIL)为1.21,预测带对实测值的覆盖度为67%.P/r模型预测结果的可靠性较高.
3)与Sartor-Boyd冲刷模型相比,P/r模型能够更准确地描述实际地表径流的携污过程,具有更广泛的适用范围,对于不能采用Sartor-Boyd冲刷模型进行模拟的情况,P/r模型可完全适用.
| [1] | Arya l R.2003.Dynamic behavior of suspended solids and particle associated micropollutants in a highway runoff.Tokyo: University of Tokyo |
| [2] | Aryal R, Kandasamy J, Vigneswaran S, et al.2009.Review of stormwater quality, quantity and treatment methods part 2: stormwater: quality modeling[J].Environmental Engineering Research, 14(3): 143-149 |
| [3] | Barrett M E, Irish L B Jr., Malina J F Jr, et al.1998.Characterization of highway runoff in Austin, Texas, Area[J].Journal of Environmental Engineering, 124(2): 131-137 |
| [4] | Bicknell B R, Imhoff J C, Kittle J L Jr, et al.1997.Hydrological simulation program-FORTRAN, user's manual for version 11.EPA/600/R-97/080.Athens, Ga.: U.S.Environmental Protection Agency, National Exposure Research Laboratory |
| [5] | Chebbo G, Bachoc A.1992.Characterization of suspended solids in urban wet weather discharges[J].Water Science and Technology, 25(8): 171-179 |
| [6] | 陈莹,赵剑强,胡博,等.2012.西安市城市主干道路面径流初期冲刷效应[J].环境工程学报,6(3): 929-935 |
| [7] | Chui T W,Mar B W,Horner R R.1992.Pollutant loading model for highway runoff[J].Journal of the Environmental Engineering Division,108(6): 1193-1210 |
| [8] | Crobeddu E,Bennis S.2011.A new model for simulating TSS washoff in urban areas[J/OL].Applied and Environmental Soil Science,http://www.hindawi.com/journals/aess/2011/318765/ |
| [9] | Deletic A,Maksimovic C T,Ivetic M.1991.Modelling of storm wash-off of suspended solids from impervious surfaces[J].Journal of Hydraulic Research,35(1): 99-118 |
| [10] | Deletic A,Maksimovic C T.1998.Evaluation of water quality factors in storm runoff from paved areas[J].Journal of Environmental Engineering,124(9): 869-879 |
| [11] | Deletic A,Ashley R,Rest D.2000.Modelling input of fine granular sediment into drainage systems via gully-pots[J].Water Research,34(15): 3836-3844 |
| [12] | Furumai H,Balmer H,Boller M.2002.Dynamic behavior of suspended pollutants and particle size distribution in highway runoff[J].Water Science and Technology,46(11/12): 413-418 |
| [13] | 韩景超,毕春娟,陈振楼,等.2013.城市不同下垫面径流中PAHs污染特征及源辨析[J].环境科学学报,33(2): 503-510 |
| [14] | Imteaz M A,Hossain I,Hossain M I.2014.Estimation of build-up and wash-off models parameters for an east-Australian catchment[J].International Journal of Water,8(1): 48-62 |
| [15] | Jack A G,Petrie M M,Ashley R M.1996.The diversity of sewer sediments and the consequences for sewer flow quality modeling[J].Water Science and Technology,33(9): 207-214 |
| [16] | Kim G,Yur J,Kim J.2007.Diffuse pollution loading from urban stormwater runoff in Daejeon city,Korea[J].Journal of Environment Management,85(1): 9-16 |
| [17] | 李怀恩,刘增超,秦耀民,等.2012.西安市融雪径流污染特性及其与降雨径流污染的比较[J].环境科学学报,32(11): 2795-2802 |
| [18] | Millar R G.1999.Analytical determination of pollutant wash-off parameters[J].Journal of Environmental Engineering,125(10): 989-992 |
| [19] | Nash J E,Sutcliffe J V.1970.River flow forecasting through conceptual models part I—A discussion of principles[J].Journal of Hydrology,10(3): 282-290 |
| [20] | Sartor J D,Boyd G B,Agardy F J.1974.Water pollution aspects of street surface contaminants[J].Journal of Water Pollution Environmental Federation,46(3): 458-467 |
| [21] | Tsihrintzis V A,Hamid R.1997.Modeling and management of urban stormwater runoff quality: a review[J].Water Resources Management,11(2): 137-164 |
| [22] | Tsihrintzis V A,Hamid R.1998.Runoff quality prediction from small urban catchments using SWMM[J].Hydrological Prcesses,12(2): 311-329 |
| [23] | US Army Corps of Engineers.1977.STORM: storage,treatment,overflow,runoff model—User's manual[R]. 723-S8-L7520.Davis,Calif,USA: Hydrologic Engineering Center |
| [24] | Whipple W Jr,Hunter J V,Yu S L.1977.Effects of storm frequency on pollution from urban runoff[J].Journal of Water Pollution Control Federation,49(11): 2243-2248 |
| [25] | 赵剑强.2002.城市地表径流污染与控制[M].北京:中国环境科学出版社 |
 2015, Vol. 35
2015, Vol. 35


