2. 华南农业大学工程学院, 广州 510642;
3. 巫山县环境监测站, 重庆 404700
2. College of Engineering, South China Agricultural University, Guangzhou 510642;
3. Wushan Environmental Monitoring Station, Chongqing 404700
水华风险预警作为水环境累积型风险预警的一种,是以水生生物群落层面为评价终点,针对水生态系统受体的逆化演替和恶化风险的分析、描述和及时报警(中国环境科学研究院,2013).由于藻类水华发生过程具有复杂性、非线性、时变性的特点(仝玉华等,2011),且是环境中多种压力源的组合效应,因此,其在警情发生状态上,需要经过一定时间的潜伏、演化和累积,从而区别于单一压力源(某个水污染事件)的突发型风险预警;其在时间尺度和预警目的上,属于短期的异常波动预警,从而区别于长期的变化趋势预警.
预警模型是近年来国内外水华风险预警研究的重要工具,一般分为机理模型(如水质水生态模拟模型)和非机理模型(如回归分析模型、人工神经网络模型、遥感反演模型)(Cracknell et al., 2001; Recknagel,2004; Teles et al., 2006;曾勇等,2007;王崇等,2009;孔繁翔等,2009).后者由于所需模型参数相对少、参数较易获取、建模和计算过程相对快速和简便,较好地适应于水华风险预警需求,在实际工作中更受青睐(Coad et al., 2014).其中,人工神经网络技术具备了模拟人脑的非线性思维模式、自学习功能强大等特点,与现代化的信息采集和集成技术结合较好,在国内外水体富营养化和水华风险预警中的应用研究尤为广泛(Recknagel,2004;仝玉华等,2011;张艳会等,2011;郝启文等,2013;Coad et al., 2014).
然而,人工神经网络模型需要大量现场监测数据驱动,用于模型的驯化和校正.事实上,现场调查常常受自然环境、现场工作条件、仪器设备状况及其他不可控因素的约束,所采集的数据在时间上存在一定非连续性.指标变量数据量少或部分指标数据量的不匹配直接影响水华风险预警模型的构建和预测精度.据此,如何更科学有效地利用已有数据还有待于研究探讨.此外,我国关于水环境风险预警的理论和实践总体仍处于探索阶段,如何更好地表征水华风险及其预警等级,亦未有定论.
因此,本文针对水华风险预警中相关影响指标数据量的缺失问题,拟首先基于多元统计理论构建一种缺失数据插补法,用于弥补现场调查数据集的缺陷;然后基于主成分分析理论,确定水华风险预警的关键输入变量;采用多层感知器(MLP)人工神经网络模型对水体水华表征指标叶绿素a浓度实施预测;最后引入风险概率的概念,提出水华风险概率计算公式并完善水华预警的风险表达.上述方法以三峡库区典型支流大宁河为案例进行验证和应用.
2 原理与方法(Principle and methods) 2.1 基于多元统计和随机理论的缺失数据补充在基于数据驱动、非机理型水体水华风险预警中,其关键影响因子的数据完整性决定了风险预警模型的优劣,因此,借助多元统计和随机理论对缺失数据的补充具有重要意义.
中心极限定理有关正态分布理论中指出,许多微小偶然因素共同作用结果的变量或指标必定服从正态分布(杨振明,2007;Hardle等,2011),考虑到水环境中各影响因子的复杂性与不确定性,其各指标可认为近似服从正态分布.假设存在某一水华影响指标浓度x1,其中,x1服从均值为μ、方差为σ的正态分布,即x1~N(μ,σ),若该指标x1样本容量N超过30时(大样本数据),则选取其中30组样本数据描绘其频次直方图,发现直方图近似符合正态分布曲线变化规律(陈玉辉,2013),且30组样本数据绝大多数落在(μ-3σ,μ+3σ)范围内.
实际工作中,部分水华相关监测指标(如TN、TP)大多以月为采样频率,由于短时期内该指标的外界环境因素相对稳定,可假定当月采样日的实测浓度数据近似该月的平均值μ.借助正态分布样本数据处理中的3σ原则(拉依达准则)(李光霁等,2007),可根据该月采样日的实测浓度数据,描绘出该月29或30 d浓度值的近似数据范围.由3σ原则可知,样本数值分布在(μ-σ,μ+σ)、(μ-2σ,μ+2σ)、(μ-3σ,μ+3σ)中的概率分别为0.6526、0.9544和0.9974.σ的取值可以参考月度实测数据集的标准差确定,以确定的σ计算样本数值分布范围的上下限值,并结合实际情况对σ进行校核.若选择0.05显著性水平下(对应概率0.9544),则该指标该月每天的浓度值范围为(μ-2σ,μ+2σ).
由于该指标浓度在该范围内的取值具有随机性,对此,根据环境指标浓度数据近似服从正态分布的特点,在满足浓度取值范围条件下,借助Matlab软件,采用正态分布随机数生成函数,如normrnd(μ,σ),生成该指标在该范围内的任意随机数,从而得到一组完整的监测指标日尺度插补数据.实际研究中,为降低任意随机数的随机性影响,可以采取多组随机值纳入计算.
2.2 基于主成分分析的影响指标降维在水生态系统中,叶绿素a浓度是反映水体中浮游植物生物量的综合指标,其影响因素较多,包括营养盐因子、光热条件因子和水动力条件因子等.各影响因素之间存在一定的相关性,部分参数信息量也必然具有一定的重复性,进而会增加问题分析的复杂性(易仲强,2011),同时也带来诸多“噪音”.因此,在已监测的多项水华影响指标中,提取识别关键影响因子和主要信息具有重要意义.
主成分分析(韩晓刚等,2013)是一种通过降维的思想来简化数据的方法,力求原始数据信息丢失最少,同时把多个指标简化为少数几个综合指标,而少数几个综合指标能尽可能的反映原始指标的绝大部分信息.设监测样本个数为n,每个样本有p个变量,构成n×p阶的原始数据矩阵,具体见式(1).

其中,当p较大时,需要对原始数据矩阵进行降维处理,将原始变量指标进行线性组合,构成少数几个相互独立的综合指标.令原始指标为x1,x2,…,xp,新变量指标为z1,z2,…,zm(m< p),则得到新变量数据矩阵,具体见式(2).
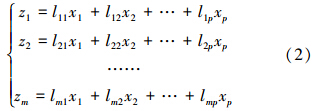
人工神经网络模型目前已有数十种,其中,理论较成熟、应用较广泛的为前向神经网络.前向神经网络中较为熟知的BP网络(Back Propagation,简称BP)侧重强调反向传播学习算法的特点,而MLP神经网络是一种特殊的多层前向网络,侧重突出其网络结构.研究中所采用的MLP网络模型是基于BP学习算法将输入的多个数据集映射到单一的输出的数据集上,其主要特点是输入与输出层之间存在一个或多个隐层;输入层没有计算节点,仅用于获取外部输入信号;网络中的信息是单向传递的,同一层中的神经元之间没有连接,通过非线性基函数的线性组合实现映射关系(刘会灯等,2008);层与层之间通常采用全连接方式,连接程度由每层连接的权值表示.隐藏层节点输出模型和输出层节点输出模型分别见公式(3)和(4).
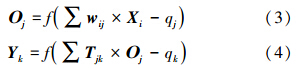
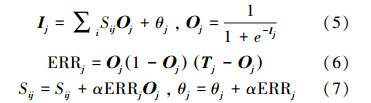
参考国内目前较公认的富营养化评价相关标准(郑丙辉等,2006),若不考虑风险概率,水华预警等级划分可以对应为:当叶绿素a浓度<10 mg · m-3时,其预警级别为蓝色预警(无警);当叶绿素a浓度为10~20 mg · m-3时,其预警级别为黄色预警(轻警);当叶绿素a浓度为20~40 mg · m-3时,其预警级别为橙色预警(中警);当叶绿素a浓度>40 mg · m-3时,其预警级别为红色预警(重警).
考虑到水华风险预警模型的输入-输出响应关系、所获取的数据质量等均具有不确定性,因此,在风险预警等级的表达中引入风险概率概念(郑恒等,2011),并提出水华风险概率计算公式如下:

三峡工程目前是世界上最大的水利枢纽工程之一,具有巨大的综合效益.然而,成库后三峡水库支流回水区富营养化问题突出,水华频发,威胁到水环境安全.大宁河是三峡水库的典型支流,位于库区腹心地带,大宁河口距离三峡大坝123 km,流域面积4045 km2,河流长度142.7 km.2003年蓄水后,受水库干流顶托,大宁河回水长度为47.2 km,至2010年(175 m蓄水)回水长度增至57.9 km.2003—2009年统计显示,大宁河共发生水华21次,占全库区支流水华发生总次数的11%;大宁河流域内,则以回水区中段白水河断面附近为水华高发区域(郑丙辉等,2009;张佳磊等,2012).
课题组于2012年1月至2013年6月在大宁河白水河断面开展了连续监测.选取叶绿素a为水华风险的表征指标和响应变量,选取与叶绿素a相关的原始监测指标纳入筛选分析和模型构建,主要包括水温WT(℃)、pH、电导率Cond(μS · cm-1)、浊度TUR(NTU)、溶解氧DO(mg · L-1)、高锰酸盐指数CODMn(mg · L-1)、总氮TN(mg · L-1)、总磷TP(mg · L-1)、流速V(m · s-1)、悬浮物SS(mg · L-1)等10项指标.其中,流速采用多普勒点式流速仪测定,CODMn、TN、TP、SS由实验室根据国家标准方法测定,频次为每月1次;其余参数数据来源于重庆市巫山县自动站多参数测定仪,频次为每天1次.
3.2 大宁河部分监测指标缺失数据插补由于原始监测指标中TN、TP、CODMn、SS等部分指标监测频次不足,导致各指标之间数据频次不一致,有必要对缺失数据进行补充.采用2.1节的数据插补方法,将大宁河每月实际采样当天TN、TP、CODMn、SS浓度作为基准,补充该月份其它天的浓度数据.选择0.05显著性水平,则大宁河TN、TP、CODMn、SS该月浓度分布在区间(μ-2σ,μ+2σ).
以2012年1月份为例,2012年1月9号的TP浓度实测值为0.065 mg · L-1,则1月份每天(不含9号)TP浓度分布在(0.065-2σ,0.065+2σ),当σ取值确定,则1月份每天的TP浓度取值范围完全确定.采用2012年1月至2013年6月共18组月度1次的实测数据,计算出18组原始数据标准差σ18=0.0424.令σ18为σ的无偏估计量,则σ= 0.0424,此时0.065-2σ<0,不符合实际情况,故需结合实际对σ估计量进行校准.考虑到时间序列数据具有一定的周期性,此处以TP历史数据中各月浓度最小值进一步校核当前各月浓度分布范围下限值.通过查阅近十年历史数据得到大宁河TP每月的最低浓度(见表 1中TP浓度下限),考虑TP浓度分布区间具有轴对称的特点,以当月浓度平均值为对称轴,可确定当月TP浓度上限,校核得到2012年1月(不含9号)每日TP浓度的取值范围0.038~0.092 mg · L-1.
| 表 1 大宁河TN与TP各月日尺度数据取值范围 Table 1 Data range of each month for TN and TP daily concentration in the Daning River |
同样地,采用类似方法确定TN浓度取值范围.2012年1月13号的TN浓度为1.82 mg · L-1,计算18组月度一次的TN实测数据标准差,可得σ18=0.2215.令σ18为σ的无偏估计量,则σ= 0.2215. 此时,2012年1月(不含13号)每日TN浓度取值范围为1.377~2.263 mg · L-1,取值范围上下限未出现负值等异常值,认为符合实际.采用该σ取值,进一步计算其余各月TN浓度取值范围(μ-2σ,μ+2σ),亦符合实际.据此,最终确定σ=0.2215,从而得到各月TN浓度取值范围(表 1).同理,确定CODMn与SS浓度取值范围分别为1.01~2.63 mg · L-1、0.66~3.74 mg · L-1,受篇幅所限,图表中仅以TN、TP为例进行说明.
依据表 1中TN、TP日尺度数据取值范围,根据2.1节随机数生成方法,采用函数normrnd可动态生成任意一组每日TP、TN浓度随机值.为降低数据随机性的影响,增加模型结果可信度,研究中选取N组(N=5)日尺度TN、TP随机值纳入模型进行模拟,避免因单一数据扰动对模型稳定性的影响.以2012年1月份为例,图 1分别描绘了所随机生成的5组不同的TN与TP日尺度数据.TN、TP数据经过插补后,与其他的叶绿素a影响因子数据频次较为统一,进而为大宁河叶绿素a模拟预测提供基础.
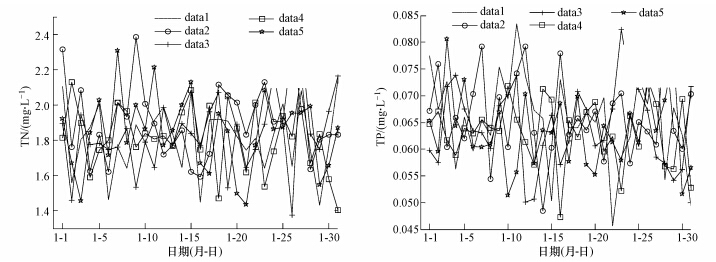 |
| 图 1 2012年1月大宁河TN和TP日尺度浓度数据随机动态补充 Fig.1 Data supplement for TN and TP daily concentration r and omly and dynamically in the Daning River in January 2012 |
以插补后的数据为基础,通过把多个监测指标简化为少数几个综合指标(主成分变量指标),实现神经网络模型输入层变量的降维.以任意一组插补后的数据为例,纳入该组数据后,共获得大宁河2012年1月1日到2013年6月14日的531组数据,涉及11项监测指标.除叶绿素a外,针对其他与叶绿素a相关的10项影响指标,基于SPSS17.0软件进行了成分分析(表 2).由于前6个主成分累积贡献率达到了80.087%,超过了80%,包含了原始数据的绝大部分信息量,故选取前6个主成分纳入模型.
| 表 2 大宁河水华影响指标的主成分分析 Table 2 Principal component analysis for algae bloom related indicators in Daning River |
表 3中进一步计算了6个主成分与原始10组指标变量之间的线性相关性,即因子载荷矩阵.例如,与主成分1(PC1)相关联因子主要是WT、TUR、CODMn、TN、SS,载荷绝对值取值范围是0.605~0.790;与主成分2(PC2)相关联因子是Cond、TP,其载荷绝对值分别是0.673、0.589.根据表 3中因子载荷矩阵,可确定2.2节式(2)中原变量xi在各新变量指标zi上的载荷系数lij.按照式(2),以10组监测指标数据及载荷系数lij,计算新变量指标zi,即主成分变量指标.后期则以6组主成分变量指标(PC1~PC6)数据作为神经网络输入层数据,从而实现了输入层变量的降维(10组减少为6组),为模型计算提供基础.
| 表 3 大宁河各主成分的因子载荷矩阵 Table 3 Component matrix for principal component in Daning River |
在指标降维的基础上,建立基于MLP神经网络的大宁河水华风险预警模型.根据MLP理论,选用6个主成分变量指标为多层感知器输入层向量,输出层选用叶绿素a浓度,采用2012年1月至2013年6月2日的数据训练MLP神经网络、构建模型.基于该模型,预测2013年6月4日至12日叶绿素a浓度值,并采用同期实际监测值进行对比验证.模型验证借助于决定系数来衡量MLP神经网络的泛化能力,决定系数范围在〖0,1〗内,愈接近于1,表明模型性能愈好;反之,则性能愈差.
研究结果显示:①5组日尺度插补数据条件下,大宁河水华风险预警模型的决定系数分别为0.9873、0.9770、0.9631、0.9738、0.9543,平均值为0.9711,叶绿素a预测结果与真实结果有较好的吻合度,模型准确性总体较高,且不同随机组的TN、TP、CODMn与SS日尺度插补数据对大宁河叶绿素a浓度预测结果影响较小(图 2a).②未实施日尺度数据插补条件下(原始数据条件下),即TN、TP、CODMn与SS每日数据不变,均直接采用当月唯一的 实际监测值,大宁河水华风险预警模型的决定系数为0.7769,叶绿素a预测结果与真实结果吻合度相对较差(图 2b).对比两种数据条件下的预测结果可知,借助于多元统计分析和随机理论对缺失数据的补充,在MLP神经网络训练样本的建立上具有一定的优势,插补数据条件下的模型准确性更高.此结果亦进一步验证了本研究中数据插补方法的可行性.
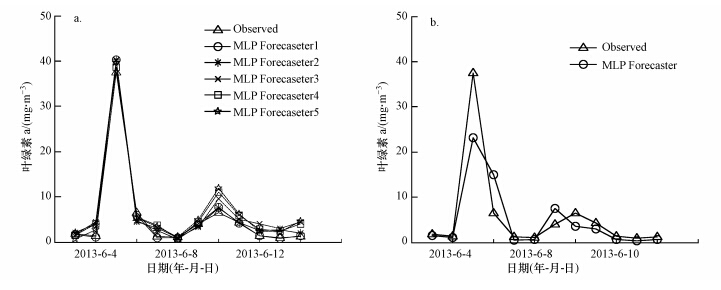 |
| 图 2 基于MLP神经网络的大宁河叶绿素a浓度预测(a.插补数据条件下,b.原始数据条件下) Fig.2 Prediction of chlorophyll a concentration based on MLP neural network in Daning River(a.with data supplement,b.with raw data) |
受原始数据收集所限,仍假定2013年6月3日至14日为未知的预测时段,进一步研究水华预警级别的划分和表达.按照2.4节方法,根据该时段内叶绿素a浓度预测结果,初步划分每天的水华预警级别.按照水华预警的风险概率计算公式(8),采用未来时段叶绿素a浓度C,计算水华平均发生概率,C选取5组模型预测结果的均值;考虑到大宁河TN、TP浓度数据补充中采用正态分布2σ原则,其置信度在0.9544概率下数据可靠,因此,数据准确率参数K值为95.44%;此外,由于基于MLP神经网络的大宁河预测模型决定系数为0.9711,因此,模型准确率参数E值为97.11%.采用公式(8),计算得到对应于每天不同预警级别的风险概率,结果见表 4.研究结果显示,预测时段内大宁河有11 d为水华蓝色预警(无警)级别,水华发生的风险概率为1.99%~18.61%;达到水华橙色预警(中警)级别的天数为1 d,水华发生概率为90.48%.
| 表 4 大宁河水华预警级别及其风险概率 Table 4 The early-warning results and its risk probability for the algae bloom in Daning River |
值得注意的是,研究中所提出的缺失数据插补法,其假定某月某日实际监测指标(如TP)浓度值为该月平均值,但实际情况下该假设并非绝对成立.目前由于受实际监测和研究条件所限,做了上述的假设处理,但其所可能引起的误差仍待进一步论证.
4 结论(Conclusions)1)本文提出了基于多元统计和随机理论的缺失数据插补法,通过大宁河案例研究和对比,结果认为该方法具有可行性,能够弥补现场调查数据不足的缺陷,减少因数据量少、数据监测频次不匹配等对水华风险预警模型精度的影响.
2)借助于主成分分析理论,充分利用水华影响因子间的相关性特点,对水体水华影响指标进行降维.针对大宁河案例研究,把10组监测指标简化为6组主成分变量综合指标PC1~PC6,以此作为水华风险预警模型的输入层变量,减少了模型运算量.
3)采用多层感知器MLP神经网络构建了大宁河水华风险预警模型.对大宁河水华表征指标叶绿素a浓度进行了模拟预测,结果发现其预测结果精度较高,模型决定系数达到0.9711.
4)提出了水华风险概率计算公式,综合考虑了水华事件的发生概率、原始数据插补的误差和模型预测精度的不足.该类耦合风险概率的预警级别划分方式,完善了水华预警的风险表达,弥补了传统预警级别划分和表达的绝对性.
5)大宁河水华风险预警结果显示,预测时段内11 d为水华蓝色预警(无警)级别,水华发生的风险概率为1.99~18.61%;1 d达到水华橙色预警(中警)级别,风险概率为90.48%.
| [1] | 陈玉 辉.2013.典型城市黑臭河道治理后的富营养化分析与预测研究[D].上海:华东师范大学 |
| [2] | Coad P,Cathers B,Ball J E,et al.2014.Proactive management of estuarine algal blooms using an automated monitoring buoy coupled with an artificial neural network [J].Environmental Modelling & Software,61: 393-409 |
| [3] | Cracknell A P,Newcombe S K,Black A F,et al.2001.The ABDMAP(algal bloom detection,monitoring and prediction) concerted action [J].International Journal of Remote Sensing,22(2/3): 205-247 |
| [4] | 韩晓刚,黄廷林,陈秀珍.2013.改进的模糊综合评价法及在给水厂原水水质评价中的应用[J].环境科学学报,33(5):1513-1518 |
| [5] | 郝启文,王小艺,许继平,等.2013.湖库水质监测与水华预警信息系统[J].计算机工程,39(1):287-289 |
| [6] | Hardle W,Simar L,陈诗一(译).2011.应用多元统计分析(第2版)[M].北京:北京大学出版社 |
| [7] | 何晓群,刘文卿.2007.应用回归分析(第2版)[M].北京:中国人民大学出版社 |
| [8] | 李光霁,孙国豪,潘家祯.2007.3σ方法在磁记忆检测中的应用[J].华东理工大学学报(自然科学版),33(5):726-732 |
| [9] | 刘会灯,朱飞.2008.MATLAB编程基础与典型应用[M].北京:人民邮电出版社 |
| [10] | 孔繁翔,马荣华,高俊峰,等.2009.太湖蓝藻水华的预防、预测和预警的理论与实践[J].湖泊科学,21(3):314-328 |
| [11] | Recknagel F.2004.ANNA-Artificial neural network model for predicting species abundance and succession of blue-green algae [J].Hydrobiologia,349(1/3):47-57 |
| [12] | Teles L O,Vasconcelos V,Pereira E,et al.2006.Time series forecasting of cyanobacteria blooms in the Crestuma reservoir (Douro River,Portugal) using artificial neural networks [J].Environmental Management,38(2):227-237 |
| [13] | 仝玉华,周洪亮,黄浙丰,等.2011.一种自优化RBF神经网络的叶绿素a浓度时序预测模型[J].生态学报,31(22):6788-6795 |
| [14] | 王崇,孔海南,王欣泽,等.2009.有害藻华预警预测技术研究进展[J].应用生态学报,20(11):2813-2819 |
| [15] | 杨振明.2007.概率论(第2版)[M].北京:科学出版社 |
| [16] | 易仲强.2011.基于ANN和SVM的三峡水库香溪河库湾富营养化预测研究[D].宜昌:三峡大学 |
| [17] | 元昌安.2009.数据挖掘原理与SPSS Clementine应用宝典[M].北京:电子工业出版社 |
| [18] | 曾勇,杨志峰,刘静玲.2007.城市湖泊水华预警模型研究——以北京"六海"为例[J].水科学进展,18(1):79-85 |
| [19] | 张佳磊,郑丙辉,刘录三,等.2012.三峡水库试验性蓄水前后大宁河富营养化状态比较[J].环境科学,33(10):3382-3389 |
| [20] | 张艳会,徐兆安,陈求稳,等.2011.基于BP人工神经网络和模糊理论的太湖蓝藻水华发生风险评价[J].长江流域资源与环境,20(9):1092-1097 |
| [21] | 郑丙辉,张远,富国,等.2006.三峡水库营养状态评价标准研究[J].环境科学学报,26(6):1022-1030 |
| [22] | 郑丙辉,曹承进,张佳磊,等.2009.三峡水库支流大宁河水华特征研究[J].环境科学,30(11):3218-3226 |
| [23] | 郑恒,周海京.2011.概率风险评价[M].北京:国防工业出版社 |
| [24] | 中国环境科学研究院.2013.流域水环境突发型风险预警技术及其示范应用[R].400011673-2009ZX07528003/01.北京:中国环境科学研究院.8-16 |
 2015, Vol. 35
2015, Vol. 35


