目前针对空气质量预报客观定量的预报方法包含两大类，即经典统计预报和数值预报.经典统计预报通过建立大气污染物浓度与气象参数间关系模型开展，此方法虽然客观，但缺乏坚实的物理基础，难以周密考虑预报因子与预报对象之间的物理联系，因子的选取也因人而异，准确率往往不够稳定.数值预报以大气动力学理论为基础，物理基础坚实，其天气形势预报已超过人的经验预报水平，并不断提高和完善，近年来在国内外得到广泛应用(王自发等，2006；吴其重等，2010；王丽涛等，2012；何东阳和黄美元，1992；de Haan et al., 2001;Olesen et al., 1992).

以美国环保署开发的第三代空气质量预报模式Models-3/CMAQ为例，美国环保署利用CMAQ提供了全美范围内超过300个主要城市的臭氧及PM_2.5预报服务(http://www.airnow.gov).国内很多研究学者也应用CMAQ在颗粒物的生成转化与传输(王丽涛等，2013；赵秀勇等，2007)、空气污染预报研究(张美根等，1999；陈焕盛等，2010；房小怡等，2004)等方面开展了大量研究，结果表明CMAQ对污染物空间分布及其变化趋势具有较强的预报能力，但由于污染源时空特征十分复杂，CMAQ污染浓度预报量与实况相比经常存在“系统性”误差(徐祥德等，2003).为提高CMAQ模型预报能力，利用监测数据对模式预报结果进行统计修正的方法应用也较为普遍(Tie et al., 2003;刘环珠等，2004).许建明等(2005)利用回归方法建立预测数据与监测数据之间的关系，降低了由于污染源不确定性产生的预报偏差.谢敏等(2012)尝试将监测数据直接作为预报初始值，结合CMAQ模式预报的增减量建立修正方法.上海市环境监测中心搭建的业务化Models-3/CMAQ数值预报系统已正常业务运行近6年，其预报成果为上海市空气质量预报与污染预警应急联动提供了重要的技术支撑与决策支持作用(王茜等，2010).本文基于CMAQ模式系统，根据起报日前期一定样本数的模式预报效果，总结出各模式预报值与实测值之间的函数关系，对预报日模式预报结果进行修正，从而建立模式修正预报方法，以修正PM_2.5预报误差.

Model-3/CMAQ是美国环保署研制的第三代空气质量预报与评估系统，由气象模式、排放模块及多尺度空气质量模式3部分组成(Foley et al., 2010)，用于模拟多种污染 物在大气中的输送与转化过程.本研究使用CMAQ v4.7.1，由气象模式WRF v3.2(Skamarock et al., 2008)提供区域气象场.大尺度气象背景场和边界条件采用欧洲气象中心的1°×1°全球gfs预报数据(24 h间隔).预报区域采用LAMBERT投影方式，中心点为118.0°E和32°N，嵌套区域为4层，网格分辨率分别为81 km\，27 km\，9 km和3 km.其中第四层区域覆盖上海及周边地区，网格数为87×72，垂直方向采用σ坐标，取不等距网格，共有20层，其中近一半分布于2 km以下，以便更好地描述大气边界层结构，地面层高度约30 m.预报区域的污染源数据来自INTEX-B源排放清单(Zhang et al., 2009)和上海市大气污染物排放清单.

为了检验模式性能，选取上海市10个国控点位，根据点位经纬度提取模式对应网格的数据与点位PM_2.5监测数据进行模拟对比，见图 1.由图 1可见，青浦淀山湖点位为对照点，不参与全市平均，其它9个国控站点覆盖人口密度较大的地区，其监测浓度反映了上海PM_2.5污染的基本水平与状况.

图 1(Fig. 1)

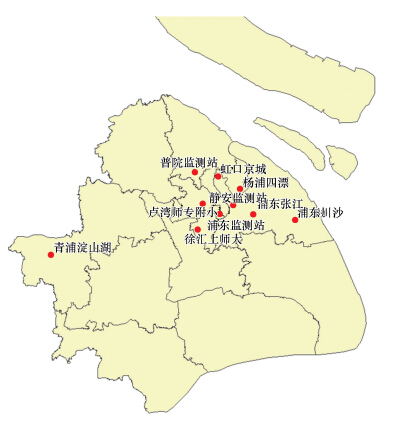图 1 上海各监测点位分布 Fig. 1 Distribution of national monitoring sites in Shanghai

选取统计检验和分级检验两种方法开展上海市PM_2.5的预报检验.统计检验主要从模拟值与观测值的绝对差异与相对偏差角度评价预报效果.选择指标包括均值偏差MB、标准化均值偏差NMB、均方根误差RMSE和标准化标准误NME(见公式(1)~(4)).分级检验主要从污染预报的角度评价预报效果，即设定一定的污染阈值，将模式预报观测对比散点图划分为4个区间(图 2).根据落在各区间中点的个数及其计算公式，来评价模式污染预报能力，选择指标包括准确率Accuracy、成功指数CSI、虚报率FAR(式(5)~(7)).

图 2(Fig. 2)

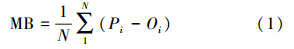
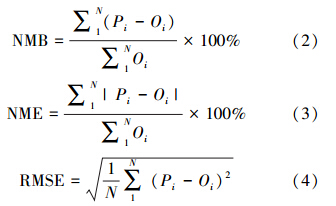
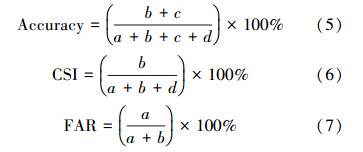
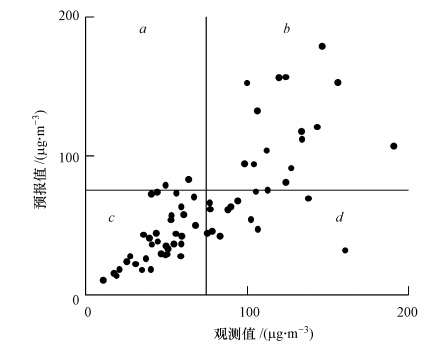图 2 分级检验计算示意图 Fig. 2 Calculation of classification index

本文应用的修正预报技术即学习型线性回归方法(DLR)，主要思路为根据起报日之前一定历史时期的模式预报效果，总结出各模式预报值与实测值之间的函数关系，假设这种关系具有一定程度的延续性，在预报时刻根据各模式预报值结合函数关系，作为最终预报结果.方法中采用多元线性回归的方法寻找历史时期各模式预报值与实测值之间的函数关系.由于模式的预报性能并不是固定不变的，可能随时间推移发生变化，因此合理的选择回归样本数目对于修正预报的效果起到至关重要的作用.由于回归时始终选择距离预报时刻最近的一段时期内模式表现作为样本，因此预报值能一定程度上体现出各模式最近一段时间的表现，从而提高模式预报的效果.

图 3和图 4给出了研究时段2013年10月—2014年1月CMAQ对上海市国控点PM_2.5日均值的模拟对比情况.可以看出，CMAQ能够较好地模拟出PM_2.5的时间变化趋势.模拟值与观测值对于较低的PM_2.5浓度，CMAQ模拟值与实测值也较为接近.模拟与实测的偏差主要出现在峰值的模拟，CMAQ模拟的峰值大小往往远小于实测值.考虑可能是由于污染源排放以及区域背景的浓度都被低估，以及上海市的大气氧化性较强，CMAQ的化学模块未能充分模拟上海市大气化学过程中气-粒过程的快速转化过程.

图 3(Fig. 3)

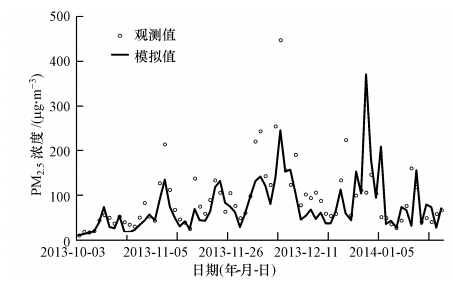图 3 2013年10月1日—2014年1月31日PM2.5日均值模拟值与观测值对比 Fig. 3 Simulation and observation of PM2.5 daily concentration between Oct. 1，2013 to Jan. 31，2014

图 4(Fig. 4)

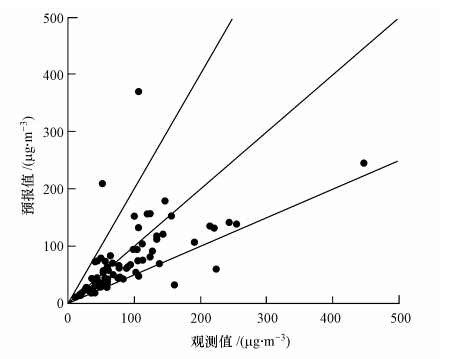图 4 上海市PM2.5日均浓度模拟值与观测值散点图 Fig. 4 Scatter diagram of simulation and observation of PM2.5 daily concentration in shanghai

表 1中列出了各研究时段上海市PM_2.5日均浓度模拟值与实测值的统计参数评估结果.可以看出，CMAQ对PM_2.5的模拟值与实测值较为接近，但存在25%的低估.各个月份模拟值与观测值的标准平均误差在29%~46%之间.当PM_2.5观测值较高时，模式模拟结果与实测相比偏差更大，如2013年11、12月份的模拟值较实测值低估最多，模拟PM_2.5浓度在这两个月低估分别达到了27%和32%.可能原因是由于11、12月份颗粒物浓度出现了峰值，高浓度污染事件较多，而模型对于峰值的模拟能力不足，从而使得总体的模拟效果不佳.另一方面的原因则可能是由于CMAQ对整个大区域背景模拟偏低引起的.由于冬季盛行偏北风，上海受来自北方的污染输入影响更大，而模型的对于区域背景模拟的偏低可能导致对污染物区域输送低估，从而导致上海市颗粒物浓度模拟的总体低估.平均偏差MB与均方根误差RMSE反映了模拟值和观测值之间的偏差和误差大小，其绝对值越小表明数值模拟结果与观测结果越接近，模拟效果越好；归一化标准因子NMB、NME考虑了不同浓度水平下模拟与观测的差异，反映了模拟值与观测值之间相对偏差和误差的大小，一般情况下，如果二者均小于50%，则认为模型模拟效果较好(Eder and Yu， 2006;Kang et al., 2007).如表 1所示，从MB、RMSE、NMB及NME来看，CMAQ的模拟结果较为准确，模拟值在可接受的误差范围内.总体来看，模式模拟结果基本能够反映上海市PM_2.5的浓度状况和变化趋势.但存在系统性低估的问题.

表1(Table 1)

表1 2013年10月—2014年1月上海市PM2.5日均浓度模拟评估 Table 1 Evaluation of PM2.5 daily concentration simulation in Shanghai between Oct., 2013 to Jan., 2014

表1 2013年10月—2014年1月上海市PM2.5日均浓度模拟评估 Table 1 Evaluation of PM2.5 daily concentration simulation in Shanghai between Oct., 2013 to Jan., 2014 研究时段 MB/(μg·m-3) RMSE/(μg·m-3) NMB NME 研究期间 -24.03 55.01 -25% 36% 10月 -5.63 13.5 -15% 29% 11月 -23.54 39.65 -27% 29% 12月 -47.38 79.82 -32% 37% 1月 -7.92 54.32 -9% 46%

为进一步评估CMAQ对PM_2.5的模拟效果，选取上海市10个国控点的PM_2.5小时浓度进行验证评估.表 2给出了CMAQ在各点位的PM_2.5小时浓度的模拟统计指标.从10个站点的平均浓度来看，CMAQ模拟的PM_2.5在不同站点均为低估.从平均值的空间分布来看，郊区点位PM_2.5的预报低估程度较高，如青浦淀山湖PM_2.5小时浓度预报偏差幅度为40.2%，浦东川沙36.5%.市区点位如普陀监测站、卢湾师专附小等PM_2.5浓度预报值的偏差幅度则较小.这可能是由于上海本地化排放清单中，郊区县排放清单的不确定性较市区大(黄成等，2011)，因此导致模拟误差相对于市区更大.普陀监测站、卢湾师专附小等点位处于上海市区，受局地源排放的影响较大.其模拟值较观测值的低估程度较小.其次，PM_2.5浓度误差的这种区域分布特征表明可能存在经上海西部进入上海的污染物区域传输，而区域排放清单采用的是2009年基础数据，导致CMAQ对于区域背景和污染输送的模拟存在低估和不足.

表2(Table 2)

表2 2013年10月—2014年1月上海各站点PM2.5模拟值与观测值的对比评估 Table 2 Evaluation of PM2.5 hourly concentration simulation in monitoring sites between Oct., 2013 to Jan., 2014

表2 2013年10月—2014年1月上海各站点PM2.5模拟值与观测值的对比评估 Table 2 Evaluation of PM2.5 hourly concentration simulation in monitoring sites between Oct., 2013 to Jan., 2014 模拟地点 浓度类型 MB/(μg·m-3) RMSE/(μg·m-3) NMB NME 普陀监测站 小时值 -17.8 69.3 -18.3% 46.1% 静安监测站 小时值 -19.8 74.0 -19.8% 46.6% 浦东监测站 小时值 -26.5 73.5 -27.8% 49.0% 卢湾师专附小 小时值 -22.3 70.3 -22.9% 45.9% 徐汇上师大 小时值 -22.4 91.1 -21.4% 49.1% 杨浦四漂 小时值 -26.2 71.7 -27.2% 47.9% 浦东川沙 小时值 -35.6 74.5 -36.5% 50.2% 浦东张江 小时值 -16.1 64.6 -22.6% 55.9% 青浦淀山湖 小时值 -23.5 75.5 -40.2% 49.7% 虹口凉城 小时值 -26.5 70.3 -22.3% 48.2%

本文采用多元线性回归的方法寻找历史时期各模式预报值与实测值之间的函数关系.由于模式的预报性能并不是固定不变的，可能随时间推移发生变化，因此合理的选择回归样本数目对于修正预报的效果起到至关重要的作用.由于回归时总选择距离预报时刻最近的一段时期内模式表现作为样本，因此预报值能一定程度上体现出各模式最近一段时间的表现，从而提高集合预报的效果.为比较修正预报效果，分别选择回归样本数2~15、20、30(即选择预报时刻前2~15、20、30天预报值和实测值作为回归样本)开展建模.为了体现预警功能，分级检验阈值选择PM_2.5浓度日均值二级标准，为75 μg · m^-3.学习回归后修正预报效果如表 3和表 4所示.可以看出，统计检验中，回归样本数不同，其各种统计检验指标结果也不同，从样本数为2到样本数为6，随着样本数增加，RMSE、NMB和NME等各指标值明显降低，这说明当样本数小于6时，随着样本数增加，PM_2.5修正预报效果明显改善.当样本数大于6，RMSE、NMB和NME等各指标值逐渐上升，即PM_2.5修正预报效果明显降低.这说明，样本数为6时，学习回归修正预报的效果明显优于其他样本数时的修正效果.主要原因可能跟天气系统的周期性有关，秋冬季节上海主要受过程性天气影响，一般天气过程周期为6~7 d(张国琏等，2010)，在同一种天气系统控制下，CMAQ模型对PM_2.5浓度的模拟效果可能存在系统性偏差.通过学习型回归方法进行修正，可以适当校正模式模拟的系统性偏差.

与未修正时CMAQ对PM_2.5浓度的模拟评估结果相比，学习样本数选择为6时，预报值与实测值的均方根误差和标准平均偏差检验效果均优于未修正CMAQ预报结果，但NME为39.3%，略高于未修正预报结果，这说明经过学习回归修正后，预报结果的趋势变化与实况拟合得更好，但在PM_2.5日均浓度出现较高浓度，而模式并未模拟出对应高值时，学习回归修正后，可适当修高模式原本模拟的低值，但在PM_2.5日均浓度下降后，这种修高模式的效应仍然存在，所以可能导致修正后预报结果较实况偏高，而未修正结果较实况偏低.

表3(Table 3)

表3 PM2.5日均浓度预报统计检验 Table 3 Statistical evaluation of PM2.5 daily concentration forecast

表3 PM2.5日均浓度预报统计检验 Table 3 Statistical evaluation of PM2.5 daily concentration forecast 学习样本数 RMSE/(μg·m-3) NMB NME CMAQ 55.0 -25.0% 36.9% DLR-2 133.9 61.4% 92.3% DLR-3 66.0 18.1% 51.2% DLR-4 53.5 12.8% 46.6% DLR-5 48.2 13.1% 41.8% DLR-6 47.3 15.0% 39.3% DLR-7 47.6 15.6% 39.3% DLR-8 49.4 16.6% 41.7% DLR-9 49.1 17.3% 40.4% DLR-10 48.4 16.4% 39.7% DLR-11 49.6 17.2% 40.9% DLR-12 52.1 19.3% 42.0% DLR-13 49.6 19.5% 40.3% DLR-14 51.5 19.7% 40.0% DLR-15 52.5 20.7% 42.0% DLR-20 75.1 34.6% 54.6% DLR-30 82.4 42.7% 62.1%

表4(Table 4)

表4 PM2.5日均浓度预报分级检验 Table 4 Classification evaluation of PM2.5 daily concentration forecast

表4 PM2.5日均浓度预报分级检验 Table 4 Classification evaluation of PM2.5 daily concentration forecast 学习样本数 准确率Accuracy 成功指数CSI 虚报率FAR CMAQ 76.4% 56.4% 12.0% DLR-2 69.2% 56.8% 30.0% DLR-3 66.7% 53.3% 29.4% DLR-4 69.1% 55.3% 29.7% DLR-5 70.1% 59.2% 31.0% DLR-6 74.2% 63.0% 25.6% DLR-7 70.8% 59.6% 28.2% DLR-8 73.4% 62.2% 24.3% DLR-9 76.2% 65.9% 21.6% DLR-10 75.8% 65.9% 21.6% DLR-11 70.5% 60.9% 26.3% DLR-12 71.7% 63.0% 25.6% DLR-13 74.6% 66.7% 25.0% DLR-14 79.3% 72.1% 20.5% DLR-15 71.9% 66.0% 27.9% DLR-20 67.3% 62.2% 31.7% DLR-30 66.7% 62.2% 32.4%

分级检验主要是检验模式对于污染预报的效果与能力，CMAQ预报的PM_2.5浓度准确率为76.4%，污染成功指数为56.4%，虚报率为12%.利用学习型回归方法进行修正，当样本数为14时，各项分级检验指标均优于其他样本数时的修正效果，准确率由76.4%提高至79.3%，成功指数由56.4%提高至72.1%，均优于未修正预报结果，虚报率则高于未修正预报值.若选择统计检验效果最好的样本数6时，成功指数为63%，也优于未修正预报结果，而准确率和虚报率则略高于未修正预报值.这也跟前文统计检验揭示的问题类似，秋冬季节上海市PM_2.5浓度水平较高，采用前7 d的监测数据进行回归修正后，可适当修高模式原本模拟的低值，提高模式对于污染预报的成功率，但当PM_2.5日均浓度下降后，这种修高模式的效应仍然存在，所以可能导致修正后模式的虚报率提高，准确率下降.而利用14 d的样本数时，样本数更多，模式修正的幅度会适当平滑，可能导致修正后的预报准确率较样本数为6时更高.

总的来说，学习型多元线性回归方法可以明显提高预报效果.统计检验和分级检验中回归样本数的选择对PM_2.5预报效果的影响不尽相同，因此，建议实际业务应用中，可同时利用两种本数进行修正预报，并根据业务预报需求来综合参考修正预报的结果.学习型线性回归方法具有普适性，未来利用此种方法对数值模式结果进行修正预报对于各城市开展环境空气质量预报具有研究意义和可行性.

1)对2013年10月—2014年1月上海市PM_2.5浓度开展CMAQ模式预报及其修正技术研究，结果显示 CMAQ模式能够较好地模拟出PM_2.5的时间变化趋势及浓度水平，模式模拟的PM_2.5浓度总体处于低估的水平，从整个研究时段来看存在约25%的低估，尤其在高污染阶段，模式的低估更为突出，达32%.

2)应用学习型多元线性回归方法建立实时动态更新的学习型线性回归方程，对PM_2.5浓度的数值预报结果予以修正，结果显示分别选取适当样本数开展学习型回归修正，PM_2.5浓度预报的标准平均偏差由原来的偏低25%降低至偏高15%，预报准确率由原来的76.4%提高到了79.3%，污染预报成功指数由56.4%提高至72.1%，明显提高了PM_2.5浓度的预报效果.说明利用监测数据对数值模式系统开展修正预报具有研究意义和可行性，并为其他城市开展预报提供了示范.