我国的土壤重金属污染问题较为突出，近年也发生了多起土壤重金属污染公众事件，如2006年甘肃徽县血铅事件、湖南“镉大米”事件等，故土壤环境质量评价作为确定污染程度和制定污染控制策略的重要参考而被广泛关注.国内外现常用的土壤环境质量评价方法主要包括：单因素指数评价法(奚旦立等，2004)、内梅罗综合污染指数法(奚旦立等，2004)、地累积指数评价法(Muller，1969)和潜在生态危害指数法(Hakanson，1980)等，这些方法可对区域土壤环境质量进行初步判别，但因土壤环境系统受自然变化和人类活动的双重影响，呈现出随机性、模糊性的特征，故在基于常用确定性方法的污染评价中仍存在一些不足(Lermontov et al., 2009；李飞等，2012；祝慧娜等，2009)，需要进一步完善，主要表现在：①由于土壤环境中重金属含量数据常存在较大空间差异性，故如果土壤重金属含量参数为单一确定性数值则易造成评价结果出现较大不确定性；②不同学者或决策者采用的地球化学背景值参数的差异及不同区域土壤类型的差别，这都造成评价结果缺乏可比性；③在评价过程中，由于各评价者对数理统计学的了解程度不一，导致出现很多数理统计学问题，降低了结果可信度.以上3点不足均可能会误导最终决策.鉴于此，近年来模糊数学方法被引入用于降低评价系统不确定性的研究与实践中，其通过隶属度函数描述土壤重金属污染状况的渐变性和模糊性，对于数据资料少或数据精度不高情况具有良好的适用性，并已有学者尝试用三角模糊数或梯形模糊数来解决上述问题，并将其成功地应用于水环境风险评价(金菊良等，2008；Li et al., 2007；Mofarrah and Husain， 2011)和土壤、河流沉积物重金属污染评价中(樊梦佳等，2010；李飞等，2012；Wang et al., 2014).但通过对这些改进评价方法的综合分析可知，改进后的重金属污染模糊评价方法仍存在以下不足：①改进后的许多方法虽然在评价过程中达到了更好的参数不确定性控制，但复杂的运算公式使改进方法的可操作性大为降低，运算时间大为增加；②现改进后的方法往往不具备配套有高认知度评级标准的综合评价功能，导致综合评级主观性较强；③采用不同的隶属函数或抽样模拟方法可能造成模型不确定性(Li et al., 2012)，现有研究中少有讨论.以上3点都会大大降低改进评价方法的可操作性和可推广性.

本研究以Hakanson潜在生态危害指数方法为基础，尝试分别将区域土壤中各重金属的实测含量值和其对应的地球化学背景值模糊化，而后分别利用Monte-Carlo抽样法和拉丁超立方抽样法(Latin Hypercube Sampling，LHS)进行平行随机模拟研究，并综合利用模型参数的筛选、参数分布检验和多元尺度分析(Multidimensional Scaling，MDS)等数据处理技术，以求建立起一套基于土壤潜在生态风险评价及溯源分析的高效决策支持系统.将所建土壤环境重金属污染评价体系应用于一个真实的污染土壤实例中，取得了较为满意的结果，以期为我国土壤重金属的污染评价、优先污染物的控制及区域污染防控决策的制定提供新思路.

瑞典科学家Hakanson于1980年提出的潜在生态危害指数法(Hakanson，1980)，其算式如下：

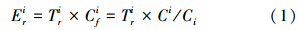
式中，Cⁱ_f为土壤重金属i的富集系数；Cⁱ为表层土壤重金属元素i的实际监测含量(mg · kg^-1)；C_i为i元素的参比值(mg · kg^-1)，本文采用区域土壤中重金属的地球化学背景值(国家环保总局，1990)；Tⁱ_r为重金属i的毒性响应系数，Cd、Ni、Zn、Cu和Cr的毒响应系数分别为30、5、1、5和2(陈静生等，1989；Hakanson，1980；徐争启等，2008)；Eⁱ_r为重金属i的潜在生态危害系数.

土壤中多种重金属的综合潜在生态风险程度，Hakanson则通过潜在生态风险指数RI来表征：

潜在生态危害指数值与污染程度级别的对应关系见表 1.

表 1(Table 1)

表 1 重金属污染潜在生态危害指数与综合污染程度划分(Hakanson，1980) Table 1 Pollution grade of heavy metals based on index of potential ecological risk(Hakanson，1980)

表 1 重金属污染潜在生态危害指数与综合污染程度划分(Hakanson，1980) Table 1 Pollution grade of heavy metals based on index of potential ecological risk(Hakanson，1980) 单种重金属潜在生态危害系数范围 单种重金属潜在生态危害程度 Hakanson潜在生态危害指数(RI)范围 重金属的潜在生态风险程度 <40 1级，轻微生态污染 <150 1级，低度生态危害 40~80 2级，中等生态污染 150~300 2级，中度生态危害 80~160 3级，强生态污染 300~600 3级，重度生态危害 160~320 4级，很强生态污染 >600 4级，严重生态危害 >320 5级，极强生态污染

三角模糊数的定义为(Zadeh，1965；Michael et al., 2008)：设在实数域R上的一个模糊数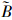，定义一个隶属函数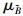：(x): [0，1]，x∈R，若隶属函数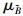(x)表示为：

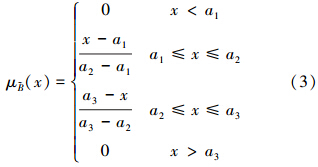
则称为三角模糊数，记作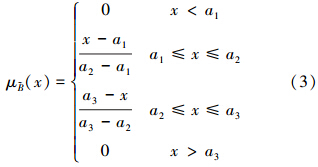=(a₁，a₂，a₃).其中，a₁≤a₂≤a₃；当a₁=a₂=a₃时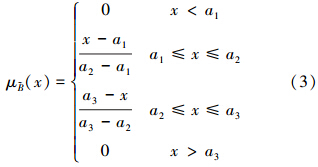，为一个精确实数，三角模糊数模糊分布见图 1(李飞等，2012).实际计算中，通常利用α-截集技术来简化计算，关于基于α-截集的三角模糊数计算法的详细内容见文献(樊梦佳等，2010；李飞等，2012).

图 1(Fig. 1)

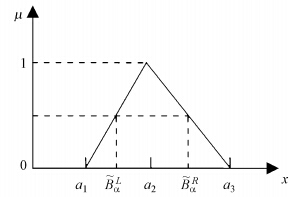图 1 三角模糊数分布曲线与其α-截集 Fig. 1 Triangular fuzzy intervals under α-cut

对于模型参数而言，存在最小值、最概然值和最大值，可以构造参数的三角模糊数(a₁，a₂，a₃)，这里a₁，a₂，a₃是实数，且a₁≤a₂≤a₃.根据数理学方法和数值上下线分析原理(Han and Kamber， 2006；Nazir and Khan， 2006)，正态或近似正态分布的数列，有95%以上的数据落入平均值±2倍标准差之间，故取值方法为：a₁值在比较数据的最小值和均值减去2倍的标准差后取较大值；a₂值取数据的统计期望值，统计期望值是反映随机变量总体大小特征的统计量，常作为描述随机变量总体大小特征的统计量，常见的有算术平均值、几何平均值和中位数等，而最终的选取需取决于随机变量的分布特征(张利田等，2007)；a₃值在比较数据的最大值和均值加上2倍标准差后取较小值.此取值方法使计算更精确.

据式(3)可知，用隶属函数除以曲线与x轴围城的面积(a₃-a₁)/2，即可得到 的可能性概率密度函数：

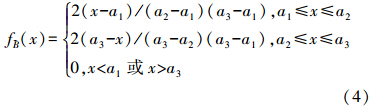
将式(3)转换为概率分布函数，再用逆变换法(王文胜等，2007)，得到可能值x的随机模拟公式：

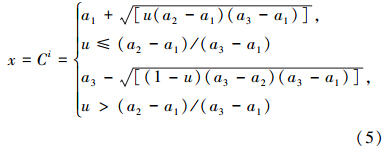
式中，u为区间[0，1]上的均匀分布随机数.可能值x的随机模拟过程，先通过计算机程序产生区间[0，1]上的一系列均匀分布随机数u₁，u₂，…，u_m，然后带入式(5)中，即可得到变量x的随机模拟系列x₁，x₂，…，x_m.通过模拟可以把三角模糊数与其函数之间的运算转化为普通实数间的运算，进而可以由模拟结果得到各可能值区间及其相应分布概率.其中，m为随机模拟的试验次数.

由于各种重金属浓度数据及地球化学背景值的选择存在的不确定性，将其分别表示为三角模糊数 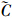ⁱ=(C¹，C²，C³)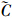，_i=(C₁，C₂，C₃)，然后再进行随机模拟，根据式(1)，可得到基于随机模糊的土壤潜在生态风险评价方法：

式中，m为随机模拟的试验次数.随机模拟可将所得到的随机数转化为输入参数的抽样值，主要方法为Monte-Carlo抽样和拉丁超立方抽样(Latin Hypercube Sampling)2种，本研究尝试分别利用这2种抽样方法进行平行研究，探索抽样模型差异可能给评价结果带来的不确定性.

在基于随机模糊的土壤潜在生态风险评价方法可信度分析中，根据潜在生态危害系数各级分级限值(表 1)，分别为40、80、160和320，推导出经随机模拟得出的各种重金属的土壤潜在生态风险系数实验值隶属于各级污染的可信度P可表示为：

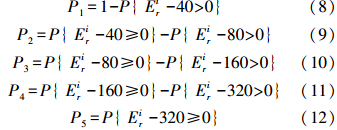
根据式(8)~(12)得出各重金属隶属于的污染程度等级及对应的概率可信度.综合潜在生态风险指数的概率可信度表达式可以此类推.

MDS是分析研究对象的相似性或差异性的一种多元统计分析方法，采用MDS可以创建多维空间感知图，图中的点(对象)的距离反映了它们的相似性或差异性(Torgerson，1965；薛薇，2009).相比于目前广泛被用于来源分析的主成分分析法(Principal Component Analysis，PCA)，MDS利用的是成对样本间相似性，目的是利用这个信息去构建合适的低维空间，使得样本在此空间的距离和在高维空间中的样本间的相似性尽可能的保持一致，以使数据降维对原始数据信息的损失尽量降低(Torgerson，1965)，故本研究采用MDS来分析土壤中重金属污染的来源.

实例源于作者2011—2012年的研究成果(李飞等，2011)，采样区域的农用土壤为褐土和潮土类，在我国的土壤分类系统中属于钙层土土纲，半干暖温钙层土亚纲.该土壤的相关特征为全剖面的盐基饱和度＞80%，pH值为7.0~8.2左右，0~20 cm的有机质为10~20 g · kg^-1左右.

经实验室采样检测后所获土壤监测数据的统计分析结果见表 2.实际监测数据经常包含一些误差较大的、无代表性的数据，故先后对所得数据进行异常数据的筛选、参数分布检验和多元尺度分析(MDS)，并分析结果.异常数据的剔除指在处理实验数据的时候，常常会遇到个别数据偏离预期或大量统计数据结果的情况，如果把这些数据和正常数据放在一起进行统计，可能会影响实验结果的正确性.区域大量的土壤重金属实测数据往往符合正态分布或对数正态分布，故此时根据数理统计学原理(中心极限定理等)，有99%以上的数据落入平均值±3倍标准差之间，故以平均值±3倍标准差作为研究的剔除原则(Evans and Olson， 2009；Han and Kamber， 2006).对于评价中超出“平均值±3倍标准差”的离群值建议对离群值对应的采样点进行进一步采样核查与单独评价，以全面地表征样本的整体性和独特性.本文相关统计计算均借助SPSS 16.0vers软件.

表 2(Table 2)

表 2 研究区域土壤重金属含量的统计描述 Table 2 Statistical description of the heavy metal concentrations in the study site

表 2 研究区域土壤重金属含量的统计描述 Table 2 Statistical description of the heavy metal concentrations in the study site 元素 统计值/(mg·kg-1) K-S Sig. S-W Sig. 最大值 最小值 平均值 国家二、三级标准值 标准差 偏度 峰度 注：国家土壤环境质量二、三级标准值取pH均＞7.0下的各重金属对应值；S-W Sig是指Shapiro-Wilk检验得出的显著性指数；“*”分别代表对应的几何均值或几何标准差. Cd 80.43 0.45 9.21* 0.6、1.0 4.74* 1.920 3.799 0.042 0.007 Ni 1355.75 98.04 510.94 60、200 383.30 1.088 1.541 0.200 0.156 Zn 1692.00 26.69 943.92 300、500 586.63 -0.212 -1.243 0.200 0.577 Cu 77.78 7.34 31.33 100、400 23.63 0.829 -0.145 0.200 0.208 Cr 100.80 7.23 36.71 250、300 29.86 1.234 1.041 0.200 0.124

将土壤实测含量参数进行Shapiro-Wilk检验，由表 2可知，Ni、Zn、Cu和Cr的sig.值均大于0.05，表明这些重金属的实测含量数据都呈正态分布，而Cd的sig.值小于0.05，故其不符合正态分布.对Cd的含量数据进一步转化验证，根据其含量数据的偏度和峰度信息，选择Ln函数进行数据的转换，转换后Ln(Cd)数据集的概率分布符合正态分布(S-W Sig.＞0.05)，故原始Cd的含量数据符合对数正态分布.

根据表 2的统计分析结果，除Cd选择几何平均值作为最概然值a₂以外，其余重金属最概然值都选用算数平均值，按2.2.1节取值方法将各重金属含量数据三角模糊化，以 ⁱ表示，见表 3.

表 3(Table 3)

表 3 经三角模糊化的实例区域土壤重金属的含量数据 Table 3 Processed heavy metal concentration data in soil of the study area

表 3 经三角模糊化的实例区域土壤重金属的含量数据 Table 3 Processed heavy metal concentration data in soil of the study area mg · kg-1 Cd Ni Zn Cu Cr (0.45，9.21，58.46) (98.04，510.94，1277.51) (26.69，943.92，1692.00) (7.34，31.33，77.78) (7.23，36.71，96.43)

C_i为地球化学背景值，考虑到实例区域可能有土壤性质或类型差异，故根据国家环保部于1990年著的《中华人民共和国土壤环境背景值》(国家环保总局，1990)，并将书中该实例区域相关采样点下的地球化学背景可能值进行三角模糊化，见表 4.

表 4(Table 4)

表 4 经三角模糊化的实例地区土壤重金属的地球化学背景值 Table 4 Processed heavy metal geochemistry background in the study area

表 4 经三角模糊化的实例地区土壤重金属的地球化学背景值 Table 4 Processed heavy metal geochemistry background in the study area mg · kg-1 Cd Ni Zn Cu Cr (0.05，0.08，0.12) (17.00，24.90，33.00) (34.70，50.90，67.30) (14.90，17.50，20.70) (40.20，57.30，73.90)

将表 3~4中经三角模糊化的实例区域重金属实测数据和其对应的地球化学背景值数据，根据式(5)~(6)，利用Crystal Ball 2000(Student edition)软件分别进行Monte-Carlo抽样下的随机模糊模拟(MC-TFN)和Latin Hypercube抽样下的随机模糊模拟(LH-TFN)，可得到潜在生态风险指数模拟序列 E^rj_i j=1，2，…，m;i=1，2，…，5，m为随机模拟的实验次数，而后分别进行10000~50000次模拟实验，由于数据量较大，暂只列出实例区域土壤中Ni的潜在生态风险评价模拟结果，见表 5.

表 5(Table 5)

表 5 基于随机模糊的潜在生态风险指数对重金属Ni的评价模拟结果 Table 5 Results of potential ecological risk assessment based on stochastic-fuzzy simulation for Ni

表 5 基于随机模糊的潜在生态风险指数对重金属Ni的评价模拟结果 Table 5 Results of potential ecological risk assessment based on stochastic-fuzzy simulation for Ni 试验次数 MC-TFN LH-TFN 平均值 最小值 最大值 平均值 最小值 最大值 10000次 131.13 50.43 336.50 131.12 51.56 343.69 20000次 131.30 50.43 342.37 131.18 51.20 344.22 30000次 131.23 50.43 342.37 131.15 50.84 344.22 40000次 131.40 50.43 348.34 131.15 50.84 344.22 50000次 131.40 50.43 348.34 - - -

由表 5可知，MC-TFN和LH-TFN模拟过程在试验次数分别为40000和30000次时结果已收敛，可见LH-TFN模拟过程的效率更高，这与一些学者的研究结果相互支持(张应华等，2007)，并且MC-TFN和LH-TFN评价过程达到结果收敛时消耗的时间均小于1.5 h，而对于同一个评价者进行基于α-截集技术的三角模糊数评价，其过程需耗时近3.5 h.为方便进行对比，故选择m=40000为平行试验的研究模拟次数.为进一步验证MC-TFN方法、LH-TFN方法和单纯的蒙特卡罗模拟方法的相对优越性，在m=40000下，分别计算了置信水平为95%和90%时实例区域各种重金属生态风险指数模拟结果之间的绝对误差值，见表 6.

表 6(Table 6)

表 6 40000次模拟下不同模拟方法评价结果的比较和绝对误差分析 Table 6 Comparison and absolute error analysis of results using different assessing methods at 40000 times simulation

表 6 40000次模拟下不同模拟方法评价结果的比较和绝对误差分析 Table 6 Comparison and absolute error analysis of results using different assessing methods at 40000 times simulation 项目 蒙特卡罗方法 MC-TFN方法 LH-TFN方法 绝对误差 90% 95% 90% 95% 90% 95% 蒙特卡罗方法 MC-TFN方法 LH-TFN方法 Cd 3504.676 3508.770 8627.717 8627.575 8656.420 8647.978 4.094 0.142 8.442 Ni 105.029 104.211 131.328 131.409 131.156 131.137 0.818 0.081 0.019 Zn 18.687 18.798 18.937 18.976 18.930 18.930 0.111 0.039 0 Cu 8.824 8.904 11.234 11.282 11.251 11.250 0.08 0.048 0.001 Cr 1.305 1.302 1.699 1.699 1.698 1.697 0.003 0 0.001

由表 6可知，采用MC-TFN方法和LH-TFN方法得出的实例区域各重金属的潜在生态危害系数值的绝对误差基本小于对应的单纯蒙特卡罗模拟方法评价结果的绝对误差，这说明随机模糊方法对贫样本或低精度样本数据有更好的适用性，表征更加准确.而对比MC-TFN方法和LH-TFN方法结果的绝对误差显示此2种方法对于不同重金属数据的模拟效果各有优劣，故建议根据绝对误差数据来进行2种随机模糊模拟方法的联合使用，这样可以使评价过程更高效、更稳健.故研究在最终的模拟中选择MC-TFN方法来处理评价Cd和Cr，而选用LH-TFN方法来处理评价Ni、Zn和Cu.

基于MC-TFN方法和LH-TFN方法联合评价结果，根据式8~12所示的结果可信度计算方法得到实例区域各种金属隶属于各生态风险污染等级的概率可信度值，如表 7所示.

表 7(Table 7)

表 7 各重金属隶属于各污染等级的可信度 Table 7 Reliability degrees of each heavy metal in different pollution levels

表 7 各重金属隶属于各污染等级的可信度 Table 7 Reliability degrees of each heavy metal in different pollution levels 重金属 轻微生态污染 中等生态污染 强生态污染 很强生态污染 极强生态污染 <40 [40, 80) [80, 160) [160, 320) >320 Cd 0 0 0 0 1 Ni 0.147 0.586 0.266 0.001 0 Zn 0.998 0.002 0 0 0 Cu 1 0 0 0 0 Cr 1 0 0 0 0

结合表 7和表 1可知，实例区域各重金属中Cd、Cu和Cr分别明确的属于极强生态污染、轻微生态污染和轻微生态污染等级，并且Zn的生态风险极可能(99.8%)属于轻微生态污染.然而，Ni的生态风险系数模拟值的隶属度分布表明在区域重金属污染评价中确实存在可以误导决策的不确定性，可以看出，Ni有58.6%的可能性隶属于中等生态污染等级，也有26.6%的可能性隶属于强生态污染，而隶属于轻微生态污染和很强生态污染的可信度(分别为14.7%和0.1%)较低.故该区域应将Cd和Ni作为污染优先控制因子，尤其是Cd需要尽快采取土壤修复措施，Ni的污染也有进一步恶化的可能，故应进一步探明污染控制因子的污染来源，以采取有针对性的治理方案.

为了进一步验证基于随机模糊理论的土壤潜在生态风险评价的准确性、适用性，在同一实例下，将基于随机模糊理论的土壤潜在生态风险评价结果、确定性潜在生态风险指数法和单因素指数方法(I_i，I_i=C_i/S_i，其中I_i表示土壤中污染物i的单因素污染指数；C_i为土壤污染物i的实测浓度的统计平均值(mg · kg^-1)；S_i为污染物i的评价标准值(mg · kg^-1)，S_i一般采用土壤环境质量标准(GB15618—1995)中的二级标准值)进行对比研究，结果排列为随机模糊评价结果、确定性土壤潜在生态风险评价结果和单因素指数评价结果，见表 8.

表 8(Table 8)

表 8 实例区域土壤中重金属的污染程度分级结果 Table 8 Rankings of the soil heavy metals pollution in case area

表 8 实例区域土壤中重金属的污染程度分级结果 Table 8 Rankings of the soil heavy metals pollution in case area Cd Ni Zn Cu Cr 5/5/15.35 2/3/8.52 1/1/3.15 1/1/0.31 1/1/0.15

由表 8可知，基于随机模糊理论的土壤潜在生态风险评价结果与确定性潜在生态风险评价结果相似，也基本符合单因素指数法关于污染与否的判断，说明该方法适用于土壤重金属污染评价.3种方法评价结果上也存在一定差异，主要包括：①在Zn的污染程度判定上，单因素指数法与确定性潜在生态风险评价、基于随机模糊理论的土壤潜在生态风险评价结果相矛盾，分析可知这是由于单因素指数法未考虑重金属自身的生态毒性差异，故导致Zn的评价结果偏高；②在Ni的污染程度判断上，确定性潜在生态风险评价等级比基于随机模糊理论的土壤潜在生态风险评价等级偏高，这很可能由于在重金属含量数据和其对应的地球化学背景值的三角模糊化计算中，其对应的取值包含更多的信息，选取范围也更大，而这有利于准确地表征实例区域污染的真实情况，关于表 7的分析也正验证了此条结论.根据表 7和表 8结果，实例区域的RI值远超600(严重生态危害)，其中98%的贡献为E^Cd_r，故100%隶属于严重生态危害等级，但本改进方法显然有了具有更高认知度的综合风险评级标准.

综上，基于随机模糊理论的土壤潜在生态风险评价法可得出评价区域各重金属风险指数的可能值区间及其隶属于各风险等级的概率水平，较好地弥补了确定性评价中的不足，且在计算效率上远超单纯的模糊评价方法，加之纳入了对抽样模型不确定性的考虑，提出了基于MC-TFN方法和LH-TFN方法的联合模拟法，使评价过程更加稳健可靠.本研究是通过对评价中参数数据的科学处理以达到降低其不确定性的目的，故对其他研究中参数处理过程均有参考意义.但本方法仍存在一定的不足：①本方法虽然运算效率得以提高，但其方法的复杂程度基本与单纯的三角模糊数运算相当，可能会阻碍方法的推广使用，故相关过程的计算机编程实现需进一步研究；②三角模糊数应用范围较广，但对于情景数据的可适度仍需要注意，不同隶属度分布对数据处理过程的影响需进一步研究.

为了进一步表征实例区域污染土壤中各重金属间的相互关系，并分析它们的污染来源，本文借助多元尺度法(MDS)进行研究.利用MDS分析实验数据，根据其拟合散点图为一条直线说明MDS构面图完全解释给定的相异性，也就是压力系数为0.根据图 2的欧氏距离模型下的二维散点图，对于实例区域土壤中各重金属的数据来说，Cr、Cu和Cd可归为一类，说明在研究区域土壤中上述3种重金属的地球化学性质是相似的，具有相同的来源或者产生了复合污染；Ni和Zn则单独各成一类，说明二者在研究区域土壤中有较为独立的特点.

图 2(Fig. 2)

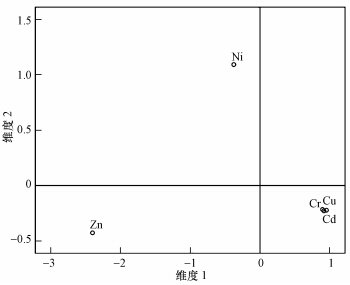图 2 欧氏距离模型下的二维散点图 Fig. 2 2-dimension MDS ordinal configuration of heavy metals in case site

土壤中重金属的来源一般可分为自然源和人为源(章明奎等，2008).自然源主要来自于岩石和矿物自然物理化学过程，人为源主要是人类活动带来的直接或间接排放的重金属，其中如采矿、金属冶炼加工、化石燃料燃烧、化肥农药的生产和使用过程等，均会造成重金属在土壤中的积累.结合研究区域特点和相关历史事件分析可知，结合表 2，Cr、Cu和Cd都有着较小的标准差，说明这3种重金属可能源于自然源和人为源共同作用，并很可能产生复合污染，而Ni和Zn的标准差很大，可见其含量分布有很显著的差异，所以其主要受人为源控制，但二者污染作用明显较为单一和独立.根据文献资料(包括区域的时序土地利用状况、当地的经济和产业结构等)(李飞等，2011；王学锋等，2005)可知当地电池企业众多，产品包括镍镉，铁镍和锌银碱性蓄电池，由于企业大量违规排放的电池废液，加上所在省灌溉水源的不足和农民的认识不足，故实例土壤中相关重金属含量较高很可能与当地常年利用电池废液灌溉有很大的关系；实例区域为种植小麦的农用土壤，小麦种植常施用复合化肥和有机肥，此两种肥料均有着较高的重金属含量，其中重金属主要包括Pb、Cd、Cr、Cu和Zn等(陈林华等，2009；李本银等，2009)，故实例土壤中的Cr、Cu和Cd可能主要源于废液灌溉和农业肥料的不当施用；Ni和Zn则主要来源于当地电池废液灌溉.

综上，有关部门应把Cd、Ni作为主要的污染控制对象，主动地采取一些生物、化学修复技术进行污染预防与治理，并也应定期监测Zn和Cu在土壤中的含量变化.

1)基于随机模糊理论的土壤潜在生态风险评价方法更适用于贫样本、低精度样本等情况，其可集成更多土壤环境信息，并可将模糊运算转化为实数间运算，运算效率高于单纯的模糊评价法，其可同时得出评价区域各重金属风险指数的可能值区间及其隶属于各风险等级的概率水平，如此可以更好的辅助决策者判别优先控制污染物和了解重金属污染的可能变化趋势，与确定性评价方法相比，能够更真实、全面地表征土壤中重金属的真实污染状态.

2)纳入对模型不确定性的考虑，提出了基于MC-TFN方法和LH-TFN方法的联合模拟法，使评价过程更加稳健可靠.

3)多元统计分析技术下的溯源结论更有助于在评价结果基础上有的放矢的进行相关环境修复决策.

4)将所建评价体系用于实例区域土壤重金属污染评价中，各重金属的潜在生态危害系数由高到低依次为：Cd、Ni、Cu、Zn、Cr，因此，Cd、Ni应为该地区土壤污染治理的主要控制因子，尤其极强生态风险的Cd亟需采取治理与修复措施，Cd污染可能主要源于电池废液灌溉和农业肥料的不当施用.