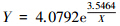总悬浮物是水体中含有的所有悬浮颗粒物质的总称，包括浮游生物、动植物遗体、浮游植物非色素细胞物质和悬浮泥沙等. 它影响着光在水体中的传播，从而影响了水体透明度、浑浊度、水色等光学性质和水生生态条件，最终决定了水体的初级生产力水平，在水质评价中起到非常重要的作用(张红等，2012).悬浮物还是水体富营养化评价中的一个重要指标，对水体中悬浮物的监测在水环境评价、水体生态环境空间差异研究以及了解水环境演化和进行水环境治理等方面具有重要的意义(乐成峰等，2008).悬浮物不仅影响湖泊、河口冲淤变化过程，同时还是各种营养盐和污染物的重要载体，易引起水华等严重生态危机(周冠华等，2009).悬浮物的时空分布特征和迁移运动变化规律，对于研究河道的冲淤变化、估算水土流失等有重要的意义.悬浮物对水体的固有光学特性，尤其波长较长的红光波段、近红外波段的后向散射能力强，这使得应用遥感技术监测悬浮物成为可能.遥感监测内陆水体悬浮物含量是通过研究水体反射光谱特征与悬浮物含量之间的关系，并建立悬浮物反演算法的基础上进行的(李素菊和王学军，2003).

在水面之上测得光谱数据与卫星成像的影像数据所受的外部环境条件有相似性，利用测得的水体表层光谱反射率数据和悬浮物浓度数据进行的反演研究，为卫星遥感反演监测水质参数奠定基础.遥感监测水质的优势明显，能宏观快速、周期性的监测，获取监测水域的全貌信息，还能反映河流从上游向下游方向悬浮物的迁移细节特征等信息，这是传统水质采样监测方法的以点代面、难以满足大面积监测所无法比的.目前水体水质遥感监测方法有3种：经验方法、半经验/分析方法和分析方法.经验方法只是简单的遥感数据与水质参数的统计关系，因其没有物理依据而很少被采用.半经验/分析模型是将悬浮物的光谱特征与统计模型相结合，具有一定的物理意义，是较为常见的方法，但众多研究者在反演时选用的模型和参数不一致(乐成峰等，2008).分析方法具有明确的物理意义，但目前其理论基础研究还不完善，并且对于二类水体而言，不同时间不同区域水体的单位固有光学特性存在较大的区别，难以对其进行有效的参数化表达，使得水质参数反演难度较大(刘忠华等，2012).这些模型和参数具有地域和时空的局限性，往往泛化能力不强.

Vapnik 在 1995 年提出一种新型统计学习方法——支持向量机 SVM(Support Vector Machines)，支持向量机具有完备的统计学习理论基础和出色的学习性能，已成为机器学习界的研究热点，并在很多领域都得到了成功应用(吴洲等，2009).最小二乘支持矢量机(Least squares SVM，LS-SVM)是标准 SVM 的一种新的扩展，用等式约束代替标准支持矢量机的不等式约束，即将二次规划问题转化为线性方程求解问题，降低了计算的复杂性，加快了求解速度和提高了抗干扰能力(孙林和杨世元，2009).最优参数的确定，是提高最小二乘支持矢量机学习和泛化能力的重要条件之一，最优参数的确定是一个难题.可用粒子群算法优化LSSVM参数，PSO(Particle Swarm Optimization，PSO)算法是由 Eberhart博士和Kennedy 博士于 1995 年提出，是一种基于迭代的优化方法(雷秀娟等，2007).在PSO算法中，每个优化问题的潜在解都假想为d维目标搜索空间中的一个点，即为“粒子(赵娜等，2013).PSO初始化一群随机粒子，用迭代的方法，在每一次迭代中，通过个体极值和邻域极值更新粒子的位置和速度，改变LSSVM的参数值，计算适应度函数值并根据其值的变化，寻找粒子的个体极值点和全局极值点，并不断更新这些极值点，直到达到最佳适应度函数值或是达到最大迭代次数，得到全局最优值，更新LSSVM的参数值为最优值.

本次研究使用改进的粒子群优化算法，迭代优化最小二乘支持向量机的参数，利用得到最优参数的最小二乘支持向量机对松花江哈尔滨段悬浮物浓度回归预测，旨在建立适用性强、精度高、能满足遥感监测、参数不多、结构简单的估算模型.

松花江发源于长白山天池，流经松花湖故而得名松花江，与另一大支流嫩江交汇于吉林松原附近形成松花江干流，之后流向东北方向与黑龙江交汇.本次研究的是松花江的中游哈尔滨段，具体研究范围是126°16′21″～126°55′10″E，45°41′56″～45°59′54″N，在流经哈尔滨松花江干流上，沿江共设置了11个采样断面，每个断面3个采样点，如图 1所示，选择水深大于1m，与岸边保持一定距离，从江北岸、江心到江南岸依次布设，共33个采样点.

图 1(Fig. 1)

图 1 采样站点位置示意图 Fig. 1 Schematic diagram of sampling sites

2012年7月14—15日，当时天气晴朗少云，无风，对松花江哈尔滨段干流上设置的采样点采集水样，同步测量水体表层光谱反射率.使用ASD公司的光谱仪进行表层水面光谱测量，该光谱仪的波普工作范围是350~1050 nm.测量时采用了唐军武等(2004)提出的在二类水体水表面以上光谱测量法，在提取离水辐射率时，使用的测量数据主要有标准灰板、天空光、水体等的光谱辐亮度数据，每个采样站点都获取10条光谱数据.在观测光谱数据的同时，采集了水表面以下20~30 cm处的水样，取出的水样立即放入冷藏箱中，当天带回实验室，悬浮物浓度采用较为常规的方法测量.同时还测量了每个站点的透明度、pH值、水深等数据，当时用GPS记录下每个采样站点WGS-84坐标.

对每个站点的10条光谱数据进行分析，删除异常光谱数据，对剩余的光谱数据计算平均值.将误差大、对研究贡献小的小于400 nm、大于900 nm以外的光谱数据剔除，保留了400~900 nm间的光谱反射率数据，如图 2所示.从图 2可以看出，有两个明显的反射峰，分别在700 nm附近和815 nm附近，750 nm附近出现反射谷.与王繁等的研究比较接近，在可见光波段出现2个反射峰，第1个反射峰在650~700 nm之间，第2个反射峰在800 nm附近，反射谷则出现在750 nm附近(王繁等，2008). 700 nm附近和815 nm附近的峰值是悬浮物含量物较高的反映，与国内相关学者的研究结果一致，在690~900 nm范围，反射率与悬浮物浓度呈正相关，且在706~900 nm范围内有较好的相关关系，达到95%置信水平下的显著相关，在819 nm处相关系数最大(李素菊和王学军，2003)；808 nm左右又出现一反射峰，该反射峰可能是由于悬浮物的散射形成的(刘忠华等，2011).

图 2(Fig. 2)

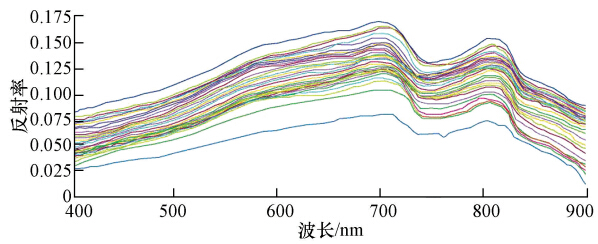图 2 水体表层反射率光谱曲线 Fig. 2 Water surface reflectance spectrum curve

粒子群算法PSO(Particle Swarm Optimization)是由Kennedy和Eberhart提出的一种启发式全局优化算法，它是一种基于群智能的演化计算方法(曾崇群等，2012).PSO算法结构简单控制容易，尤其对于动态目标函数，它的性能更加稳定，是一种启发式算法，所需的代码和参数相对较少.算法求解的优劣，不完全依赖于对初始值的选取，设定适应度函数，利用群体与粒子自身的适应度来共同引导粒子向最优解进化，保证了算法的快速收敛性.该算法表现出出色的个体学习进化和与邻域个体交流的能力，每个粒子都能通过自身经验与邻域最优个体经验，进行当前位置和速度的更新，计算过程具有内在并行性和内涵并行性，搜索是从一组解迭代优化到另一组解，可同时处理群体中多个个体，能有效的提高计算效率，对于复杂的、特别是高维多峰的优化计算具有很强的优越性，粒子群算法还具有鲁棒性，个别个体的异常不影响整体的优化.对于大多数的非线性函数优化问题比GA在速度和精度上都有提高(封磊等，2005).

粒子群优化机理的本质为粒子从其个体及全局极值中获得更新信息，并在此基础上进行随机和局部搜索(高海兵等，2005).粒子群中粒子代表问题一个可行解，每个粒子具有位置和速度两个特征，粒子位置坐标对应的目标函数值可作为粒子的适应度，算法首先初始化一群随机产生的粒子，然后通过迭代找到最优解，在每一次迭代中，每个粒子通过跟踪两个“极值”来更新自己(刘淳安和何俊红，2009)，这两个极值分别是个体极值pbest和全局极值gbest，粒子在找到这两个极值后，根据公式(1)、(2)来更新位置和速度，动态调节自身的搜索方向，寻找问题的最优解.

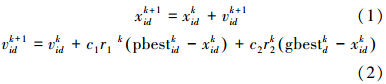
式中，x^k+1_id是粒子i第k+1次迭代中第d维的当前位置；v^k+1_id是粒子i第k+1次迭代中第d维的速度； c₁、c₂为粒子的加速因子；r₁、r₂是[0，1]之间的随机数；pbest^k_id是粒子i第k次迭代后所经历最好位置第d维分量；gbest^k_d是粒子群第k次迭代后所经历的的最好位置第d维分量.以上是经典粒子群位置和速度更新算法.

Vapnik在1995年提出的一种新型统计机器学习方法-支持向量机SVM(Support Vector Machines)，SVM在很大程度上解决了模型选择、非线性、维数灾难和局部极小点等问题.SVM是基于结构风险最小化原则，成功的解决神经网络过学习或欠学习问题，提高了泛化能力(梁洪锁，2009).算法通过核函数将实际问题经过非线性变换转换到高维空间，再在高维特征空间中进行线性回归，保证有很好的泛化能力，又使算法的复杂程度与维数无关.

求解支持向量机不需知道非线性映射的具体形式，只需要选择适合的核函数，这样就可以把高维空间的点积转换为低维空间的核函数进行计算，巧妙地解决在高维特征空间中求解带来的维数灾难问题(梁洪锁，2009).

目前常用的核函数主要有：

(1)线性核函数(Linear kernel)：

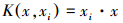
(2)多项式核函数(Polynomial kemel)：

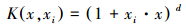
其中，d为多项式阶次；

(3)径向基核函数(RBF kernel)：

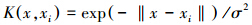
LSSVM是Suykens和V and ewalb在1999年提出的，是将最小二乘估计引入支持向量机中.它是采用将等式约束代替不等式约束作为损失函数，训练过程由二次规划问题求解转化为线性方程组求解，同时使误差平方项达到最小化的计算过程(黄磊等，2010).LSSVM只需确定核函数的形状参数和惩罚系数，不需要选取不敏感损失函数的值，将二次规划问题转化为求一组线性方程组的解，同时又不会改变核函数的映射关系和全局最优的特性(梁洪锁，2009).

低维空间中的线性回归问题可用公式(3)表述：

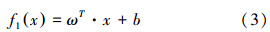
复杂的非线性回归问题，可通过非线性变换x→φ x，将原低维输入空间的回归问题映射到高维特征空间中，然后在高维空间进行线性回归，得到公式(4)：

根据结构风险最小化原理，综合考虑函数复杂度和拟合误差，引入结构风险函数，将回归问题转化为二次优化问题：

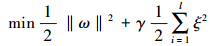
约束条件为：

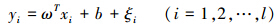
求解该优化问题，把约束优化问题变成无约束优化问题，引入拉格朗日(Lagrange)函数：

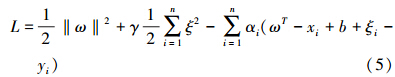
最优的α和b通过KKT(Karush kuhn Tucker)条件获得：

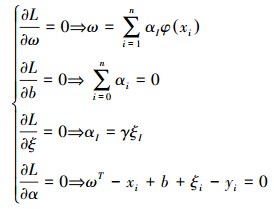
式中，ω是权重向量；γ是正则化参数；ξ_i是松弛变量；α_i是拉格朗日算子.

此优化问题转化为求解如下线性方程组，见式(6)：

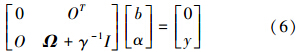
式中，y= y₁，y₂，…，y_n ^T，O= 1，1，…，1 ^T，α= α₁，α₂，…，α_N ^T，Ω 为一个n×n的方阵，K x_i，x_j 为核函数，i，j= 1，2，…，n

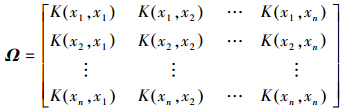
得LSSVM的拟合模型，见式(7)：

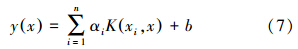
式中，α、b是线性方程组的解；n为训练样本个数.

由上面过程可以看出，只需确定核函数的形状参数σ²和正则化参数γ，不需要选取不敏感损失函数的ε值，LSSVM计算过程复杂程度得到简化.

LSSVM是基于统计学习理论的机器学习方法，能有效的解决小样本、非线性、局部极小值等问题.其参数的优化是一个难题，其中正则化参数γ和核函数形状参数σ²是两个必须调整的关键参数.本次采用改进的PSO算法优化这两个参数.

改进的PSO优化算法既避免了寻优过程过早陷入局部最优，又保证了寻优过程具有较快的收敛速度，使得参数寻优的效率大大提高.粒子在n维空间中以一定的速度飞行，在自身和种群最优个体的影响下，不断改变自己的速度和位置，飞向目标及种群中心.

改进的PSO算法速度和位置更新公式：

式中，v_id^k+1为第i粒子第k+1次迭代的速度； x^k_id是第i粒子第k次迭代中第d维的当前位置； c₁、c₂为粒子的加速因子；r₁、r₂、r₃是[0，1]之间的随机数；pbest^k_id是第i粒子第k次迭代后所经历最好位置d维分量；gbest^k_d是粒子群第k次迭代后所经历的的最好位置d维分量；pavg^k_d为粒子群第k次迭代平均位置d维分量；ω_k，ω_max，ω_min为第k次迭代时惯性权重值、惯性权重最大值和惯性权重最小值；K_max为最大迭代次数.

粒子群优化算法中，一般ω取值较大的时候，全局寻优搜索能力强，局部搜索能力减弱.在初期ω取值较大，使其具有较强的全局搜索能力，快速收敛到最优解所在的局部区域，不会陷入局部最优解；后期取值减小，趋于局部搜索，粒子主要是在当前解的附近搜索，直至找到最优解.本次研究中，ω_max=1.2，ω_min=0.2；加速常数c₁、c₂代表了粒子向自身最优解和全局最优解推进的随机加速权值，c₁=1.5，c₂=1.7，一般取值在0~4之间，本次取值在一定程度上侧重全局搜索能力；参数r₁、r₂用于保证群体的多样性，是[0，1]之间均匀分布的随机数；x^k+1_id、v^k+1_id随机初始化初值；设置粒子群规模最大值为20；最大迭代次数K_max=100，K初始值设置为0；根据随机产生的初始种群计算初始适应度.

从改进PSO算法的进化方程式(8)、(9)和式(10)可以看出，在进化计算的早期引入粒子的局部平均位置，这样避免改进PSO算法过早陷入局部极值；同时，惯性权系数随着迭代次数的增加而线性衰减，其对收敛速度的影响会逐渐减弱；而且，改进PSO算法中仍然保留粒子群的全局最优位置，加快了改进PSO算法的收敛速度.实际上，改进PSO算法中所引入的粒子局部平均位置，其实质相当于在具有动态惯性权重的PSO算法中增加了一个扰动项.正是该扰动项的引入，增加了粒子群群体的多样性，有助于粒子摆脱局部极值点(曾崇群等，2012).

PSO优化LSSVM参数的流程见图 3.

图 3(Fig. 3)

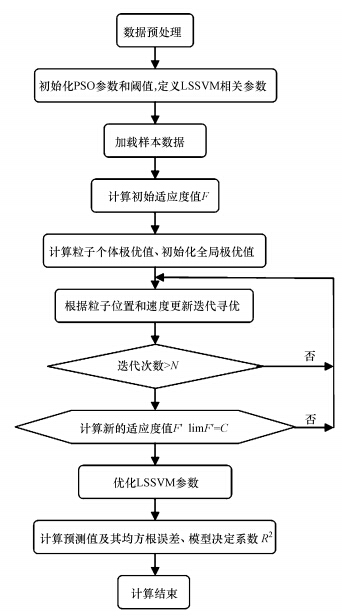图 3 PSO优化LSSVM参数流程图 Fig. 3 Flow chart of optimizing the parameters of LSSVM based on PSO

本次适应度函数的设置，见公式(11)：

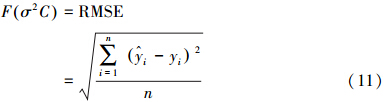
式中，RMSE为均方根误差；σ²为核函数形状参数；C为惩罚系数；_i，y_i为测试样本的预测值和观测值；n为测试样本数.

33个采样点观测数据中，删除4个异常值样本点(样点1、23、26、29的光谱反射率出现异常波动)，随机选取20个样本点作为训练集，用于建模，基本统计信息见表 1；剩余9个样本点作为测试集，用于模型验证，基本统计信息见表 2.

表 1(Table 1)

表 1 松花江哈尔滨段悬浮物20个随机建模样本的基本统计值 Table 1 Statistical characteristics of 20 random training samples of suspended solids at the Harbin section in the Songhua River

表 1 松花江哈尔滨段悬浮物20个随机建模样本的基本统计值 Table 1 Statistical characteristics of 20 random training samples of suspended solids at the Harbin section in the Songhua River 采样 点数 最大值/ (mg·L-1) 最小值/ (mg·L-1) 平均值/ (mg·L-1) 标准差/ (mg·L-1) 20 113.4 27.5 60.37 25.08

表 2(Table 2)

表 2 松花江哈尔滨段悬浮物9个验证样本的基本统计值 Table 2 Statistical characteristics of 9 testing samples of suspended solids at the Harbin section in the Songhua River

表 2 松花江哈尔滨段悬浮物9个验证样本的基本统计值 Table 2 Statistical characteristics of 9 testing samples of suspended solids at the Harbin section in the Songhua River 采样 点数 最大值/ (mg·L-1) 最小值/ (mg·L-1) 平均值/ (mg·L-1) 标准差/ (mg·L-1) 9 111.5 34.8 77.41 25.21

用各采样点的光谱反射率数据作为特征变量，悬浮物浓度数据作为目标变量，根据LSSVM计算要求，需对选用的波段光谱反射率数据作归一化处理.很多国内学者研究了悬浮物的响应波段，总悬浮物浓度最优反演波段范围为 730～832 nm(氧气吸收带除外)(刘忠华等，2011)；计算各样点散射系数与总悬浮物浓度的相关系数，得知波长675 nm处相关性最好(姜广甲等，2010)；在690~900 nm范围，反射率与悬浮物浓度呈正相关，且在706~900 nm范围内有较好的相关关系，达到95%置信水平下的显著相关，在819 nm处相关系数最大(李素菊和王学军，2003).悬浮物浓度与归一化反射率在455.08~650.17 nm附近为负相关，最大负相关出现在533.38 nm附近，r=-0.70；悬浮物浓度与归一化反射率在711.87~918.07 nm之间正相关系数最大(巩彩兰等，2006)；由于 750 nm 以后藻类颗粒物、非藻类颗粒物和CDOM 的吸收都降至 0，研究半分析模型波段选择在 750 ～900 nm 之间，此时纯水的后向散射也降至非常低可以忽略(周晓宇等，2013).

根据前人的研究成果，本次研究中分别对各波段光谱反射率与悬浮物浓度计算相关系数，结果830 nm处相关系数最大，为0.601；对不同波段光谱反射率作比值运算处理，可以部分消除大气影响，还可以一定程度消除在空间上和时间上水面粗糙度变化的影响，研究中分别计算两个不同波段光谱反射率比值与悬浮物浓度间的相关系数，结果700 nm与750 nm波段处光谱反射率比值(R₇₀₀/R₇₅₀)与悬浮物浓度相关性最大，相关系数为0.736，本次研究中以比值R₇₀₀/R₇₅₀为特征变量，以悬浮物浓度为目标变量，建立模型.

应用Matlab软件，使用LSSVM工具箱并编写程序，程序中用改进的PSO优化LSSVM的参数，主要有正则化参数γ和核函数形状参数σ².

算法优化参数的具体步骤：

1)各参数的初始化设置：设定学习因子c₁=1.5、c₂=1.7，c₁、c₂取值一般在0~4之间；最大迭代次数N=100，种群规模n=20，一般取值0~100之间；随机初始化各粒子的位置x_i0(x_i0=(x_max－x_min)×r and (1，1)+x_min)，随机初始化各粒子的速度 V_i0(V_i0=V_max·r and (1，1))；初始化惯性权重因子ω₀(ω₀=ω_max)，其值随着迭代按照公式(9)衰减，值的变化范围为1.2～0.2.

2)根据初始种群以及各粒子的位置，按照公式(11)计算每个粒子适应度函数值F(x_ij)，找到每个粒子的pbest值为当前位置用_i=x_i表示，将所有pbest中适应值最优粒子的位置及适应值存于gbest中，用=minf(x_i)，(i=1、2……n)表示.

3)根据迭代次数和种群规模，设定粒子飞行的最大速度和最小速度，利用式(8)和(10)更新粒子的位置和速度.

4)每一次迭代后更新粒子的位置、优化γ和σ²，计算适应度函数F的值，比较F值的变化，达到一常数值后不再变化满足需要；最后判断是否达到最大迭代次数，如果满足停止条件，搜索停止，否则转到步骤(2).

5)根据训练生成的模型，用测试样本进行验证，计算悬浮物的预测值及预测值的均方根误差RMSE、模型决定系数R².

在本次研究中，对于精度较关键和敏感的核函数形状参数σ²，取值范围为[0.01~100]；对于泛化能力影响明显的正则化参数γ，取值范围为[0.1，1000].经过100次迭代优选后，γ为7.02，见图 4；σ²为10.7，见图 5.

图 4(Fig. 4)

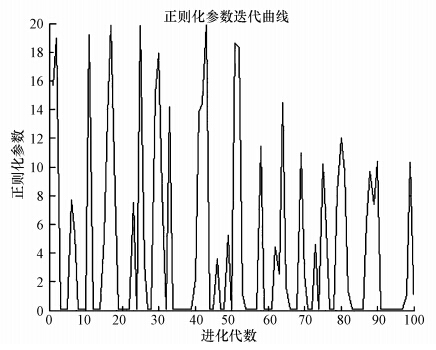图 4 正则化参数变化曲线图 Fig. 4 Dynamic curve of regularization parameter

图 5(Fig. 5)

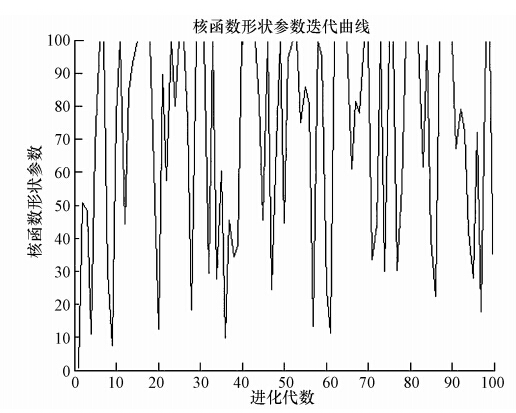图 5 核函数变化曲线图 Fig. 5 Dynamic curve of Kernel function

从图 6可以看出，适应度值很快向最佳值接近，达到最佳适应度值后趋于稳定，用时短效率高.从结果看，所建模型的决定系数R²为0.901，20个样本点的均方根误差RMSE为11.50 mg · L^-1，平均绝对百分误差MAPE为10.83%.实测值与预测值间有很好的对应关系，相关系数达0.96，基本上呈线性均匀分布，见图 7，说明所建模型具有较高的精度.

图 6(Fig. 6)

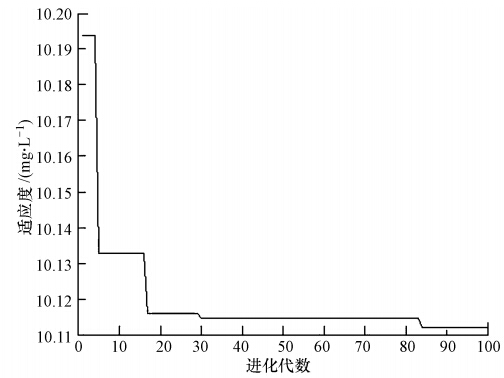图 6 适应度曲线变化 Fig. 6 Dynamic of fitness curve

图 7(Fig. 7)

图 7 悬浮物浓度实测值与预测值关系 Fig. 7 Relationship between observed and predicted data of suspended solids concentration

模型精度高不一定说明模型具有好的预测能力，为验证模型的预测能力及稳定性，将9个测试集样本点带入模型中，结果实测值与预测值的最大相对误差为17.53%，最小相对误差为1.52%，见表 3，平均绝对百分误差MAPE为10.72%，均方根误差RSME为10.11 mg · L^-1，验证模型决定系数R²为0.952，均略高于建模的决定系数R²、MAPE和RSME.总体说明，所建模型具有较好的反演精度和稳定性.

表 3(Table 3)

表 3 松花江哈尔滨段悬浮物9个验证样本实测值与预测值比较 Table 3 Comparison of observed and predicted suspended solids data of 9 validation samples at the Harbin section in the Songhua River

表 3 松花江哈尔滨段悬浮物9个验证样本实测值与预测值比较 Table 3 Comparison of observed and predicted suspended solids data of 9 validation samples at the Harbin section in the Songhua River 采样点号 实测值/ (mg·L-1) 预测值/ (mg·L-1) 相对 误差 2 111.5 92.7 16.86% 4 96.8 84.3 12.91% 18 55.4 53.6 3.25% 24 34.8 40.9 17.53% 13 95.4 85.1 10.80% 9 59.4 58.5 1.52% 20 62.7 55.4 11.64% 10 95.2 83.1 12.71% 12 85.5 77.6 9.24%

研究中分别建立了反演悬浮物浓度的波段比值模型、单波段模型，分别使用波段比值模型、单波段模型和BP神经网络方法对悬浮物进行回归预测，将结果与改进的PSO-LSSVM模型反演结果进行对比，分析评价PSO-LSSVM模型的反演精度和稳定性，见表 4.

表 4(Table 4)

表 4 不同构建模型方法比较 Table 4 Comparison of different methods used to build the models

表 4 不同构建模型方法比较 Table 4 Comparison of different methods used to build the models 建模方法 自变量 数学模型* 建模数据 验证数据 R2 RMSE/ (mg·L-1) MAPE R2 RMSE/ (mg·L-1) MAPE 注: X为波段遥感反射率，Y为悬浮物浓度. PSO-LSSVM R700/R750 0.901 11.50 10.83% 0.952 10.11 10.72% BP神经网络 R700/R750 0.862 16.17 18.65% 0.887 15.74 18.23% 单波段 R830 X 0.528 16.79 21.42% 0.890 14.29 17.09% 波段比值 R700/R750 Y=180.6545-87.9676X 0.621 15.53 20.09% 0.723 15.36 20.04%

研究中分别计算了各波段光谱反射率与悬浮物浓度间的相关系数，发现830 nm处相关系数最大，为0.601，以830 nm处光谱反射率为自变量，悬浮物浓度为因变量，分别建立了线性、二次函数、立方、指数和乘幂等数学模型，发现指数模型拟合精度最高，以指数模型作为单波段模型反演悬浮物浓度的拟合方程(见表 4).

对不同波段光谱反射率作比值运算处理，可以部分消除大气影响，还可以一定程度消除在空间上和时间上水面粗糙度变化的影响，研究中分别计算两个不同波段光谱反射率比值与悬浮物浓度间的相关系数，结果700 nm与750 nm波段处光谱反射率比值(R₇₀₀/R₇₅₀)与悬浮物浓度相关性最大，相关系数为0.736，以700 nm与750 nm波段处光谱反射率比值(R₇₀₀/R₇₅₀)为自变量，以悬浮物浓度为因变量，分别建立了线性、二次函数、立方、指数和乘幂等数学模型，发现线性模型拟合精度最高，以线性模型作为比值模型反演悬浮物浓度的拟合方程(见表 4).

BP 神经网络(Backpropagation Neural Network)是一种重要的前向神经网络模型(Yang et al., 2012)，BP 算法的特点在于利用计算网络输出后的数据误差来估计输出层的直接前导层误差，再用这个误差估计更前一层的误差，如此就获得了所有其他各层的估计误差(陈志强等，2013).以700 nm与750 nm波段处光谱反射率比值(R₇₀₀/R₇₅₀)为输入变量，以悬浮物浓度为输出变量，建立了BP神经网络模型，其拓扑结构包括输入层、隐藏层和输出层，其中输入层和输出层均为1层，隐藏层为10层，对该模型进行多次训练，得到700 nm与750 nm波段处光谱反射率比值(R₇₀₀/R₇₅₀)与悬浮物浓度间的试验参数，确定映射关系.

以上结果可以看出，对于本次悬浮物的遥感反演，从模型精度和稳定性方面看，机器学习的统计分析方法比传统的统计分析方法效果好.对于非线性，小样本的预测，作为机器学习的统计分析方法PSO-LSSVM模型优于BP神经网络模型.

1)本次利用随机选取的20个样本为建模样本，剩余的9个样本为验证样本，用传统的单波段模型、比值模型和BP神经网络模型，对于小样本数据往往回归精度不高.而机器学习的统计学习计算方法最小二乘支持向量机LSSVM，能较好的解决样本小、非线性、局部极小值等问题，用等式约束代替不等式约束，将二次规划问题转化为求解线性方程组，需要的参数减少，简化了计算复杂程度，提高了效率，但其参数确定比较难.

2)本次采用改进的PSO算法优化LSSVM参数，充分利用其寻优过程简单易控制，迭代收敛速度快，搜索全局最优解效率高等优点，寻优得到LSSVM的最优参数，用随机选取的 20个样本为训练集，训练得到模型参数，用剩余的9个样本验证，得到模型预测悬浮物浓度均方根误差RMSE为10.11 mg · L^-1，平均绝对百分误差MAPE为10.72%，模型决定系数R²为0.952，该精度可以满足实际预测需要.

3)根据待反演的水质参数浓度值，用改进的PSO优化LSSVM的核函数形状参数σ²和正则化参数γ，得到的核函数形状参数σ²可以保证模型反演精度，得到的正则化参数γ可以使模型具有较好的泛化能力，用来对其它水质参数遥感预测提供参照，为卫星遥感监测水质奠定基础.