2. 中国科学院大学, 北京 100049;
3. 北京市环境保护监测中心, 北京 100048;
4. 北京师范大学全球变化与地球系统科学研究院, 北京 100875
2. University of Chinese Academy of Sciences, Beijing 100049;
3. Beijing Municipal Environmental Protection Monitoring Center, Beijing 100048;
4. College of Global Change and Earth System Science, Beijing 100875
目前,我国正面临严重的大气污染问题,频繁发生的大气污染事件给人民生活带来了很大影响,对大气污染进行准确预报的需求非常迫切.能较为完整反映气象、源排放以及其它物理化学过程影响的数值预报方法是开展大气污染预报的重要手段,然而,由于数值模式采用的排放源、初始条件、物理化学参数仍存在较大不确定性,使得目前空气质量数值预报的不确定性仍然较大,在很大程度上影响了模式预报的可信度.之前的研究表明提高模式输入数据(如排放源)的精度和模式分辨率能在一定程度减小预报不确定性,但在无法直接减小模式自身不确定性时,合理认识和描述模式不确定性对人们了解预报及其不确定性反而更加重要(Russell and Dennis, 2000).因此,能在很大程度上考虑和描述模式不确定性的集合预报方法开始得到发展,已成为一种提高预报效果的有效方法和手段(杜钧,2002).
在国际空气质量预报上,Monache和Stull(2003)开展了臭氧的集合预报试验,发现集合成员预报的平均值比单模式预报结果更接近实际观测值.在Monache研究的基础上,Pagowski等(2005)在臭氧集合预报中引入了Krishnamurti等(2000)的加权集成方法,即根据集合成员的预报误差大小来对其预报结果进行加权集成,发现加权集成的预报效果比单个模式预报和集合平均预报都好.Mallet和Sportisse(2008)、Mallet等(2009)通过多个物理参数化方案、多种模式分辨率、多个初始条件等的相互组合构建了48个集合成员的空气质量集合预报系统,发现对集合成员预报结果进行简单平均并不能显著改进预报,需引入一些其它集成方法才能有效改进预报性能.在国内,空气质量集合预报研究也已逐步开展.王自发等(2008)首次在污染物沉降模拟中应用了多模式权重平均集合技术.唐晓等(2010)利用蒙特卡罗随机模拟方法对模式的输入数据和参数进行了集合扰动,构建了包含50个集合成员的臭氧集合预报系统,并开展了臭氧概率预报的尝试.王自发等(2009)基于美国的Model-3/CMAQ模式、CAMx模式和中国的NAQPMS模式构建了业务化多模式空气质量集合预报系统(EMS),该系统对3个模式的模拟区域、排放源数据、气象场数据进行统一设置,实现3个模式在同一硬件平台上自动化运行,能提供未来72 h城市空气质量的集合预报结果.这一系统是全球少数的业务化空气质量多模式预报系统之一,已成为北京、上海、广州等城市业务化空气质量预报的重要工具之一.然而,该集合预报系统的预报性能仍主要依赖不同模式成员以及模式成员算术平均的预报效果(陈焕盛等,2013),并没有将观测信息有效应用于空气质量预报的优化.虽然传统观点认为多模式算术平均的预报结果优于单一模式的预报结果,但已有研究表明多模式预报算术平均的预报效果并不总是好的(McKeen et al., 2005),特别是当集合预报系统的集合成员数较少时.
针对EMS存在的上述问题,本研究尝试将一种统计集成方法-多元线性回归引入到EMS中,利用其将历史观测信息纳入到EMS预报体系,并对EMS 3个模式成员的预报结果进行集成.本研究以北京市环境监测中心业务化运行的多模式集合预报系统(EMS-Beijing)和北京市28个空气质量监测站点的观测数据作为基础,分析多元线性回归方法对2010年4月北京多模式的PM10预报结果进行集成预报的效果,分析影响集成预报的关键因子.本研究将为EMS在业务化空气质量预报上的拓展应用和性能提升提供参考.
2 模式系统和观测数据(Model and Observation)本研究采用的模式系统是中国科学院大气物理研究所设计研发的空气质量多模式集合预报系统(EMS),该系统以中国科学院大气物理研究所自主开发的NAQPMS模式,美国的Model-3/CMAQ模式和CAMx模式为核心,将3个模式集成到统一软硬件平台上,气象驱动场采用第5代中尺度气象模式(MM5),初始场资料采用美国大气海洋局(NOAA)的数值天气预报中心(NWP)GFS数据集AVN分析资料,以每日世界时12时(北京时20时)为起始预报时间,向后预报72 h.模式系统能全自动化运行,每日提供城市尺度72 h的空气质量预报,图 1给出了集合预报系统的总体框架.这一系统已应用于北京、上海等城市空气质量预报,为这些城市业务化空气质量预报提供实时预报数据.
 |
| 图 1 EMS-Beijing的模式框架系统 Fig. 1 Frame of ensemble air quality multi-model forecast system for Beijing(EMS-Beijing) |
本研究重点针对北京市环境监测中心业务化运行的北京多模式空气质量实时预报系统(EMS-Beijing)进行分析和集成研究.为了方便不同模式预报结果的集成并减小区域设置不同而引起的模式差异,EMS-Beijing中不同空气质量预报模式采用统一的区域设置,以北京为核心区域模式设置为4重 嵌套网格.第一区域覆盖中国地区,第二区域覆盖华北地区,第三区域覆盖京津冀地区,第四区域覆盖北京地区,其中第四区域范围如图 2所示.4个区域水平分辨率分别为81 km、27 km、9 km和3 km,粗分辨率模拟区域为其嵌套的子区域提供边界条件.这一嵌套设置的主要作用在于减小人为设置的边界条件对北京空气质量数值模拟的不利影响,同时在北京地区实现高分辨率的数值模拟,提高数值预报精度.中尺度气象模式MM5为各空气质量模式提供统一的气象场输入数据,排放清单按照网格区域的大小分为区域源、华北地区排放源和北京及周边地区排放源,统一由SMOKE排放源模型处理,通过气象-化学及排放源-化学交互模块实现MM5气象模式及SMOKE排放源模型与空气质量模式的对接(吴其重等,2012).
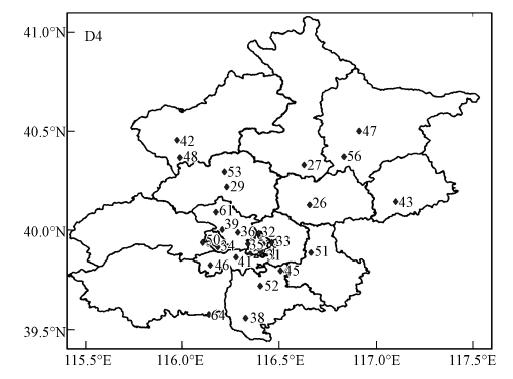 |
| 图 2 第四区域范围和站点分布 Fig. 2 The 4th model domain and distribution of monitoring stations |
本文模拟数据为EMS-Beijing在2010年1—4月期间的PM10日均值预报数据,所有预报数据来自模式第4区域的预报结果,根据2010年我国执行的空气污染指数(API)标准,利用当日12时至次日11时的PM10小时预报值计算日均值.观测数据为北京市环境监测中心28个站点(表 1)2010年1—4月的PM10日均观测浓度,站点位置见图 2.
| 表1 站点编号和站点名称 Table 1 Number and name of each station |
多模式集合预报系统提供多个模式的预报结果,在业务化空气质量预报中,为了提供确定性的预报结果,需要将不同模式结果集成起来.算术平均集成是最常用的方法,即将所有集合成员预报值的算数平均作为确定性预报结果.一般情况下,算术平均集成可以过滤掉不同集合成员的不可预报因素,给出总体的预报趋势,其预报技巧往往大于单个模式,甚至比高分辨率模式预报更加准确.但正如引言所述,已有许多研究表明算术平均集成的效果并不总是理想.本文采用一种线性回归集成方法,以期进一步改进EMS-Beijing系统空气质量预报的准确率.
3.1 线性回归集成方法介绍假设对污染物浓度进行了n次独立的预报试验,根据回归模型:

实际预报过程中,通过有限次数(n次)的观测和对应的预报试验对预报对象进行估计,得到预报对象观测值O的估计值 和预报值M,则回归模型的向量表达式即:
和预报值M,则回归模型的向量表达式即:

公式(2)中, 、M、A分别是预报要素的实际估计值,模式计算结果及其对应的回归权重.根据最小二乘原理,回归集成目的是使预报对象的实际观测向量 O与回归集成向量
、M、A分别是预报要素的实际估计值,模式计算结果及其对应的回归权重.根据最小二乘原理,回归集成目的是使预报对象的实际观测向量 O与回归集成向量 之间的误差为极小值,以使得集成预报量能够最大限度的反映预报对象的实际观测.因此,以n次观测值与回归集成值的误差平方和判断集成效果的好坏.误差平方和Q写为:
之间的误差为极小值,以使得集成预报量能够最大限度的反映预报对象的实际观测.因此,以n次观测值与回归集成值的误差平方和判断集成效果的好坏.误差平方和Q写为:
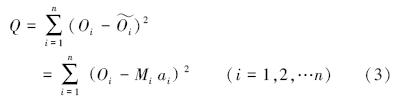
在式(3)中,误差平方Q是关于系数A的非负二次式,因此Q存在极小值.极小值存在的条件为:
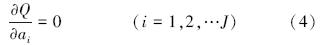
在式(2)两边同乘以 M的转置矩阵M′,得到:
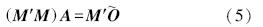
当 M′M满秩时,逆矩阵(M ′M)-1存在,则系数矩阵A 可以表示为:
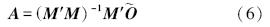
通过上式即可计算出回归模型中系数A的最小二乘估计.
在构建回归集成模型时,本文通过前期研究对比了基于所有站点数据回归集成和基于单站点数据回归集成的预报效果,发现基于单站点数据构建回归集成模型更能提高整体预报效果.因此,在每个站点利用PM10历史数据对每个站点分别进行线性回归,以单模式的预报结果作为回归集成的因子,对历史观测和预报值构成的样本进行回归,求得的系数用于对应站点未来一天预报结果的集成.该方法的回归方程简写为:
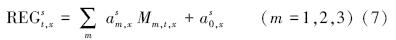
式中,am代表利用训练阶段数据回归求解的权重系数,a0为常数项,表示模式值与观测值的系统偏差.系数am,xs和a0,xs应使得误差平方和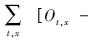
 最小化.
最小化.
试验中,基于历史数据开展回归分析求解回归方程权重系数的阶段称之为训练时段,利用回归方程对多模式预报结果进行集成并提供未来一天预报的阶段称为预报阶段.例如,将2010年4月1日作为预报的第1天,若将训练时长暂定为N d(后文将对最佳训练时长的选取进行讨论),则将预报天之前的N天数据进行线性回归,回归得到的系数用于模式对2010年4月1日PM10预报结果的集成.
3.2 评估指标介绍为定量评估不同模式和集成方法的预报技巧,采用系统偏差、均方根误差和相关系数3个统计量来评估预报系统,具体计算公式如下.
系统偏差:

均方根误差:
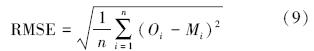
相关系数:
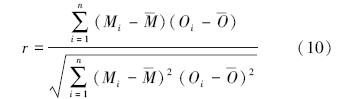
式中,n代表样本个数,M表示模式模拟浓度,O表示观测浓度.表中统计参数从不同角度刻画预报系统对污染物浓度预报的准确程度.系统偏差表征由于模式中输入场误差、排放源设置不合理和模式物理参数化等因素导致的预报结果与观测的平均偏差量,相关系数反映了模式预报值在变化趋势上与观测变化趋势的一致程度,均方根误差则表示了模式的平均误差水平.
4 主要试验结果(Results and discussion) 4.1 单模式预报技巧评估为了了解多模式集合预报系统中不同模式的预报能力和特点,首先评估了集合预报系统中3个空气质量预报模式(CMAQ、CAMx和NAQPMS)对2010年4月北京PM10变化的预报能力,从空间分布和时间序列两个方面分别进行评估.从图 3(a)可以看出,观测的PM10月均浓度在北京南部高,北部郊区低.从模式预报结果来看,3个模式对PM10平均浓度都存在不同程度的低估,其中CAMx低估最为严重,其预报结果在整个北京地区都显著低于观测值,CMAQ和NAQPMS能较好预报出北京城区PM10高值,但在其它区域也显著低估了PM10浓度.这种偏差一方面可能与模式自身物理化学过程的误差有关,另外也可能与模式源清单对北京郊县源排放低估有关,Tang 等 (2013)的源清单反演结果也发现北京郊县的一氧化碳排放可能存在显著低估.
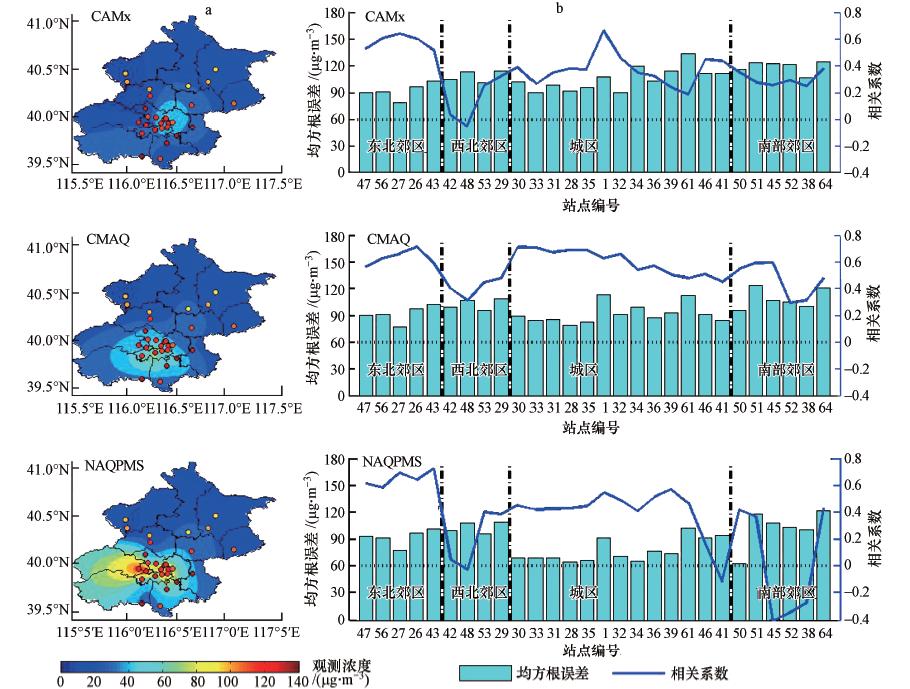 |
| 图 3 单模式的空间预报浓度分布和误差分布(a. 图为各模式模拟的浓度分布,底图为模式模拟浓度分布,填色点代表观测浓度,b. 图为各站点的相关系数和均方根误差,所有站点的相关系数均通过显著性检验) Fig. 3 Simulated PM10 concentration and error distribution by single model(Figure a shows simulated and observed concentration; Figure b shows RMS error and correlation coefficient of each station,correlation coefficients at all stations are significant) |
图 3b给出了3个模式预报PM10均方根误差和相关系数在各个站点的分布.按照观测的污染物浓度分布和地理位置综合考虑,将北京划分为东北郊区、西北郊区、城区、南部郊区四个区域,分析3个模式在不同区域的预报效果.从图 3b可以看出,不同模式在4个区域的预报技巧相差甚远,总体来看,3个模式在东北郊区和城区的预报技巧高于西北郊区和南部郊区,但3个模式在这些站点的预报误差都较大,所有站点的预报均方根误差都大于60 μg · m-3.在3个模式中,CAMx模式PM10预报的均方根误差最大,这可能与其存在较大系统偏差有关.CMAQ模式PM10预报与观测的相关系数最高,表明CMAQ模式对PM10浓度变化趋势的预报优于其它两个模式,但其预报均方根误差大于NAQPMS模式.NAQPMS模式预报的均方根误差整体低于其他两个模式,表明NAQPMS模式预报值与观测值更为接近,但其在西北郊区和南部郊区对PM10变化趋势的预报能力较差.模式对郊区污染模拟能力较差,可能与气象模式MM5对郊区风场的模拟误差较大有关,另外郊区靠近第四区域的边界,边界的粗网格数据对这一区域污染物浓模拟误差也有一定影响.
从上面评估结果可以看出,虽然3个模式预报的PM10浓度空间分布与观测浓度分布较为相似,但仍存在较大的系统低估.此外,从表征预报技巧的统计指标来看,不同模式的预报技巧存在较大差异,同一模式在不同区域的预报技巧也有很大不同,没有某一个模式的预报技巧完全优于其它模式,有的模式对PM10变化趋势的预报较好,有的模式对PM10量值的预报与观测更为接近.这个结果也在一定程度上说明,对不同模式预报结果进行集成,将不同模式的预报优点结合起来,可能能够提高系统对PM10预报的整体性能.
4.2 集成预报技巧评估为了充分利用3个模式提供的预报信息,并将历史观测信息纳入到预报中,利用3.1节介绍的多元线性回归方法对3个模式预报结果进行集成.为了评估线性回归集成方法对PM10预报的改进程度,表 2给出了3个单模式、算术平均集成和线性回归集成方法在28个站点的PM10预报的统计参数平均值,该值可以反映出预报方法在空间的整体应用效果.在利用历史模式预报数据和观测数据构建回归模型时,采用的训练时长为36 d,即利用过去36 d的观测和预报数据来确定回归模型的权重系数,这是通过敏感性试验获得的最优训练时长,敏感性试验的具体结果将在后面详细讨论.
| 表2 各个预报方法的统计指标比较(站点平均) Table 2 Statistical parameters comparison of different forecast methods(averaged by 28 sites) |
从表 2可以看出,集合预报中最常用的平均集成方法对各项指标的提高并不显著,其预报的系统偏差低于CAMx和CMAQ模式,但与观测的偏差仍达到72.0 μg · m-3,比NAQPMS模式的预报偏差高28%,表明其并不能有效修正预报的系统偏差,其预报的均方根误差大于NAQPMS模式预报的均方根误差,其预报结果与观测的相关系数小于CMAQ模式预报的相关系数.这个结果表明算术平均集成的预报结果并不能完全优于单模式预报,这与目前集合预报成员的预报结果都存在显著的系统偏差有关,也与目前集合预报系统的模式成员相对较少有关.采用多元线性回归方法对3个模式预报结果进行集成后,PM10预报的系统偏差大幅减小至5.8 μg · m-3,几乎完全修正了预报的系统偏差,预报的均方根误差也显著小于单模式预报和算术平均集成的预报,比算术平均集成的预报均方根误差低37%,比CAMx、CMAQ、NAQPMS模式的预报均方根误差分别低43%,38%和32%.多元线性回归集成对PM10变化趋势的预报改进不太显著,但其观测的相关系数仍与对趋势预报技巧最高的CMAQ模式非常接近.综合3个预报统计指标来看,多元线性回归集成的预报技巧显著高于单模式预报和算术平均集成预报.
为了进一步了解多元线性回归集成在不同站点对PM10预报的改进效果,从不同区域挑选了具有代表性的4个站点进行分析,4个站点分别为城区中心的奥体站(S32),东北郊区的顺义站(S26),西部近郊区的定陵站(S53),南部郊区的琉璃河站(S64).图 4给出了多元线性回归集成与多模式算术平均在这些站点预报的PM10浓度与观测PM10浓度的时间序列对比以及散点对比.从图中可以看出,多模式算术平均的预报结果对这些站点的PM10浓度都存在显著的估计偏差,预报的PM10浓度变化趋势平缓,对污染过程的预报能力较差,而线性回归集成显著减小了模式预报的系统低估,使大部分预报结果落在置信区(图 4b的3条红线之间)内,并且使得对高浓度PM10污染过程的预报技巧得到显著提高.
 |
| 图 4 4个站点模式与观测的时间序列(a)和相关关系示意图(b)(图b的红线以内区域为置信区域) Fig. 4 Time series of simulated and observed concentrations(a) and their correlations(b)(the region among red lines of figure b are confidence regions) |
总的来说,相对多模式算术平均方法,多元线性回归集成方法纳入了历史观测信息,能较好订正不同站点PM10预报的系统偏差,使预报结果更加贴近观测浓度的变化,也使得这些站点PM10预报结果都显著优于多模式算术平均的预报结果.这个结果也表明,当空气质量集合预报系统的模式成员存在较大系统偏差时,利用多模式集合平均来提供确定性预报结果并不能获得好的预报效果.因此,在利用多模式集合预报开展业务化空气质量预报时,有必要评估模式成员的系统偏差,并且通过有效统计集成方法将观测信息纳入进来,是改进空气质量预报的有效手段.
在实际预报中,人们更关心对污染事件的预报命中率,因此,本文利用ROC曲线来检验多元线性回归集成预报对污染事件的预报准确率.ROC是基于双态分类联列表对双态事件进行检验,常用于对异常事件的检验.对于污染事件的发生或者不发生,预报可分为几种情况:预报准确,漏报,空报和正确否定.命中率(hit rate)TPR=预报准确次数/(预报准确次数+漏报次数),假警报率(false alarm rate)FPR=空报次数/(空报次数+正确否定次数).根据国家空气质量标准,本文将PM10日均浓度大于150 μg · m-3定义为污染事件.图 5给出了多元线性回归集成预报在各个站点的ROC点,其中对角虚线表示不具有任何预报技巧的随机猜测线,当预报的ROC点位于虚线上方且相对虚线的垂直距离越远,则说明对污染事件的预报技巧越高.从图 5可以看出,大部分站点的ROC点都位于虚线上方,说明多元线性回归集成预报在大部分站点对PM10>150 μg · m-3的 污染事件具有较高的预报技巧.单模式预报和集合平均预报都有较大的系统偏差,对污染事件的命中率几乎为0,而经过多元线性回归集成纳入了历史的观测信息,修正了系统偏差,提高了对污染事件的预报命中率.
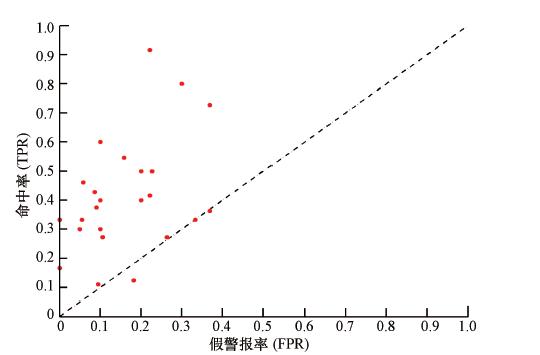 |
| 图 5 PM10污染阈值为150 μg · m-3时各个站点ROC单点分布(红点代表各个站点的ROC点) Fig. 5 ROC analysis points distribution when PM10 therhold is 150 μg · m-3(red point is ROC point of each station) |
训练时长是多元线性回归集成的关键参数,表征着需要多长时间的历史观测数据才能构建好的回归集成模型.为了分析训练时长对多元回归集成预报效果的影响,并寻求最优的训练时长,本文分析了训练时长对多元线性回归集成预报的均方根误差以及与观测相关系数的影响,分别计算了训练时长为1~70 d情况下两个预报性能指标的变化情况.图 6给出了所有站点平均的均方根误差和相关系数随训练时间长度的变化.可以看出,当训练时长小于6 d时,多元线性回归集成预报的均方根误差高于多模式算术平均的预报均方根误差,与观测的相关系数也低于多模式算术平均的预报结果.这个结果表明,如果训练时长过短,多元线性回归集成并不能有效提高PM10预报技巧.随着训练时间的增加,多元线性回归预报的均方根误差呈现逐步下降趋势,其与观测的相关系数呈现逐步上升趋势,当训练时长大于14 d时,多元线性回归集成的预报均方根误差和相关系数两项统计指标同时优于多模式算术平均预报.当训练时长大于30 d后,多元线性回归集成预报的均方根误差和相关系数对训练时长的敏感度下降,增加训练时长对预报技巧影响较小,在训练时长为36 d时的预报均方根误差和相关系数两项指标达到最好,这也是本文分析主要选用36 d作为多元线性回归集成训练时长的原因.以上试验结果表明,训练时长是影响多元线性回归集成预报效果的关键参数,不恰当的训练时长会导致集成预报技巧显著降低.因此,在利用多元线性回归来集成多模式集合预报系统的预报结果之前,需要通过有效试验分析来确定构建多元线性回归模型的最优训练时长.
 |
| 图 6 各站点的平均误差随训练时间长度的变化(蓝色实线为线性回归方法的RMSE随训练时长的变化,红色实线为线性回归方法的相关系数随训练时长的变化,蓝色虚线为集合平均方法的RMSE水平,红色虚线表示集合平均方法的相关系数水平) Fig. 6 Averaging error of all sites at different lengths of training time(blue line is RMS error,red line is correlation coefficient; solid line is for linear regression method,dash line is for ensemble mean method) |
本文对北京多模式空气质量集合预报系统的三个模式成员(CMAQ、CAMx和NAQPMS)在2010年4月的PM10预报效果进行了评估,并引入多元线性回归方法对三个集合成员的预报结果进行集成,评估这种集成方法对PM10预报性能的影响.结果发现:
1)不同模式的预报技巧存在较大差异,没有某一个模式的预报技巧完全优于其它模式,CMAQ对北京地区PM10变化趋势的预报性能优于其它两个模式,NAQPMS对PM10量值的预报与观测更为接近.
2)当集合预报系统的模式成员存在较大系统偏差时,利用算术平均提供确定性预报结果并不能获得好的预报效果;采用多元线性回归将历史观测信息纳入进来对集合成员预报结果进行集成,可大幅减小北京地区PM10预报的系统偏差和均方根误差,使其对北京地区PM10预报性能显著优于单模式和多模式算术平均的预报.
3)多元线性回归的集成预报效果与构建回归模型的训练时长密切相关,训练时长过短构建的回归模型并不能有效提高北京PM10预报技巧,选择恰当的训练时长可使集成预报效果达到最优.
本研究仍具有一定局限性.首先,本文分析的北京多模式空气质量集合预报系统的集合成员相对较少,系统主要考虑考虑物理化学过程参数化的不确定性,对初始条件和排放源等关键输入数据的不确定性没有考虑,使得集合预报结果可能不能涵盖真实的大气污染状态.如能在集合预报系统对这些不确定性进行恰当考虑,并增加集合预报成员数,可能会进一步提高多元线性回归集成的预报效果.其次,本研究侧重分析多元线性回归对PM10预报的改进效果,其对其它污染物的预报改进程度有待进一步研究,如果其对PM2.5等污染物预报也具有类似的改进效果,将能有效提高多模式集合预报系统(EMS)对业务化空气质量预报的支撑力度.
| [1] | 陈焕盛, 王自发, 吴其重,等2013. 空气质量多模式系统在广州应用及对 PM10 预报效果评估[J]. 气候与环境研究, 18(4): 427-435 |
| [2] | 杜钧. 2002. 集合预报的现状和前景[J]. 应用气象学报, 13(1): 16-28 |
| [3] | Krishnamurti T N, Kishtawal C M, Zhang Z,et al. 2000. Multimodel ensemble forecasts for weather and seasonal climate[J]. Journal of Climate, 13(23): 4196-4216 |
| [4] | Mallet V, Sportisse B. 2008. Ensemble-based air quality forecasts: A multimodel approach applied to ozone[J]. Journal of Geophysical Research, 111(D18): D18302 |
| [5] | Mallet V, Stoltz G, Mauricette B. 2009. Ozone ensemble forecast with machine learning algorithms[J]. Journal of Geophysical Research, 114(D5): D05307 |
| [6] | McKeen S, Wilczak J, Grell G,et al. 2005. Assessment of an ensemble of seven real-time ozone forecasts over eastern North America during the summer of 2004[J]. Journal of Geophysical Research: Atmospheres, 110(D21), doi: 10.1029/2005JD005858 |
| [7] | Monache L D, Stull R B. 2003. An ensemble air-quality forecast over western Europe during an ozone episode[J]. Atmospheric Environment, 37(25): 3469-3474 |
| [8] | Pagowski M, Grell G A, McKeen S A, et al. 2005. A simple method to improve ensemble-based ozone forecasts[J]. Geophysical Research Letters, 32(7), doi: 10.1029/2004GL022305 |
| [9] | Russell A, Dennis R. 2000. NARSTO critical review of photochemical models and modeling[J]. Atmospheric Environment, 34(12/14): 2283-2324 |
| [10] | 唐晓, 王自发, 朱江,等2010. 北京地面O3的集合预报试验[J]. 气候与环境研究, 15(5): 677-684 |
| [11] | Tang X, Zhu J, Wang Z F, et al. 2013. Inversion of CO emissions over Beijing and its surrounding areas with ensemble Kalman filter[J]. Atmospheric Environment, 81: 676-686 |
| [12] | 王自发, 庞成明, 朱江,等2008. 大气环境数值模拟研究新进展[J]. 大气科学, 32(4): 987-995 |
| [13] | 王自发, 吴其重, Alex Gbaguidi,等2009. 北京空气质量多模式集成预报系统的建立及初步应用[J]. 南京信息工程大学学报: 自然科学版, 1(1): 19-26 |
| [14] | 吴其重, 徐文帅, 赵秀娟, 等. 2012. 北京市大气可吸入颗粒物排放源空间优化及模式验证[J]. 环境科学学报, 32(10): 2548-2558 |
 2015, Vol. 35
2015, Vol. 35


