国内早期填埋场基本上都是依自然地形地势，简单填埋未经任何处理的生活垃圾和工业固体废物(庞会从等，2010；李航等，2009；詹良通等，2011). 这些非正规填埋场(Irregular Solid Waste L and fill，ISWL)不仅影响城市环境卫生，制约土地的直接开发，而且污染周边土壤和地下水(Slack et al., 2007; Sheesley et al., 2011; 周北海等，2000)，影响居民身体健康(韩华等，2011；赵威等，2014). 《北京市“十一五”时期环卫专业规划》明确提出了要对非正规填埋场进行整治和治理. 通过环境风险评估，可识别ISWL的环境危害及危害程度，为ISWL的管理和处置提供决策支持，因此具有十分重要的意义(Masi et al., 2014；Thapinta and Hudak， 2003).

ISWL的环境风险评估，需要详细的环境特征数据，如：场地地形地貌、气候气象以及水文地质等数据. 然而区别于正规填埋场：1)多数ISWL在建设过程中没有进行详细的水文地质勘测，缺乏环境风险评价所需的大量基础数据；2)ISWL库容小而数量相对较多. 按照传统的环境风险评估流程(风险识别、源项分析、后果计算和风险评价)评估ISWL的环境风险，不仅费时费力，而且调查成本也会非常高昂．因此，为平衡风险评价结果可靠性与评价成本间的矛盾，同时又能客观描述ISWL对周围环境和人体健康构成的风险，采用层次化风险评价技术显得尤为重要(姜林等，2011；Crawford et al., 2003)．在污染场地风险评价领域，欧美许多国家均强调应用层次化风险评价思路，以避免在调查阶段投入过多不必要的资源(ASTM，2002；ME，2011; Vik et al., 1999; The Interstate Technology and Regulatory， 2008)．我国在风险评价领域起步相对较晚，虽然相关技术导则中业已提及采用层次化思路开展污染场地风险评价，但实际评价过程中鲜少采用(姜林等，2013；钟茂生等，2013). 而据文献调研显示，在废物处置设施风险评价领域，无论国内还是国外都没有发现层次化思想的应用.

本研究通过系统分析填埋场建设、运行和封场的工艺工程和环境特征，将填埋场渗漏风险的发生发展划分为3个阶层，采用不同风险表征方式和评估方法逐层评估不同阶层的风险，从而构建了ISWL渗漏风险评价的层次化风险评价模型. 文章最后以西北某解毒铬渣填埋堆场为例，详细介绍了实际评估项目中如何开展层次化风险评估，比较了开展不同层次评价时评价结果和工程成本的差异，以期为国内大量ISWL的环境风险评估提供借鉴和参考，为其管理和处置提供决策支持.

根据ISWL渗滤液渗漏及其环境风险的产生过程(见图 1)，将ISWL的环境风险分成3个层次：第1层次是由于防渗层的可能破损导致的渗滤液渗漏；第2层次是渗滤液渗漏后对土壤和地下水的污染；第3层次是污染土壤和地下水对人体健康构成危害的过程.当第1层次的渗漏风险大于风险可接受水平时，则进行后续的第2层次风险评价. 若第2层次风险评价结果显示地下水的污染风险水平很高时，则进行第3层次人体健康风险评价，反之则评价终止. 关键是确定不同层次的风险表征方式及其可接受水平.

图 1(Fig. 1)

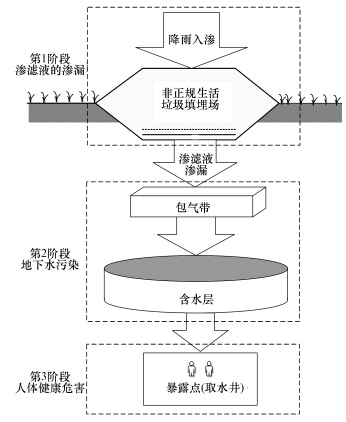图 1 填埋场渗漏污染风险评价的概念模型 Fig. 1 Conceptual model of pollution risk assessment on leakage of leachate

(1)基本原理和方法

风险，即为不利事件的发生及其可能性.因此定义第1层次风险(渗漏风险)为渗漏事故的发生及其概率. 渗漏事故的不确定性是指由于渗漏量和组分浓度计算模型及模型参数的不确定性，导致的计算结果的不确定性. 考虑到填埋场渗漏的普遍存在，认为当且仅当渗漏量和污染组分浓度超出某一标准值(可接受值)时，才认为是渗漏事故. 其中渗漏量的标准值取70 m³ · hm^-2 · a^-1，污染组分浓度的标准值参考GB18918—2002《城镇污水处理厂污染物排放标准》的限值要求.

图 2(Fig. 2)

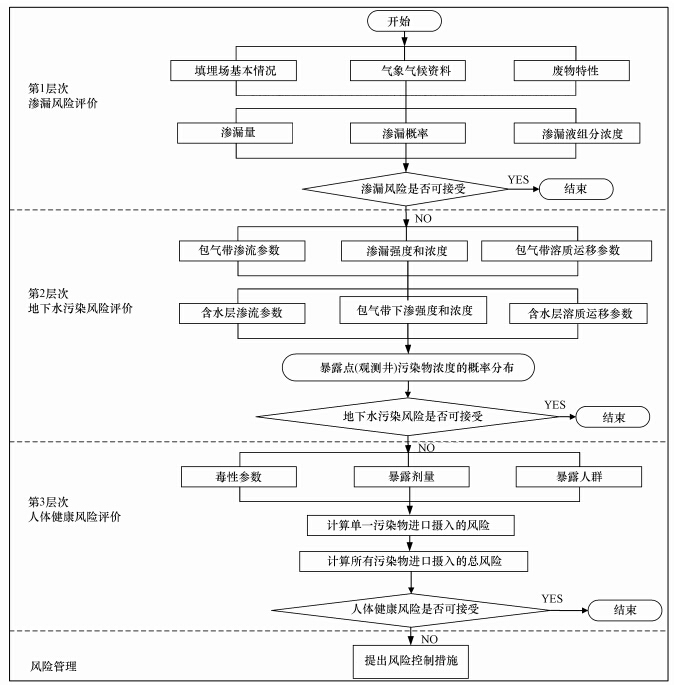图 2 非正规填埋场层次化环境风险评价的基本思路和流程 Fig. 2 Flow-process diagram of hierarchical environment risk assessment of ISWL

(2)渗漏风险的表征

假设在参数不确定性影响下，根据模型计算得到的渗漏强度Q、渗滤液中污染组分的浓度C分别服从概率分布F(Q)和F(C)，其风险大小P_C和P_Q根据下式计算：

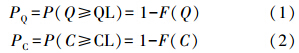
当P_C和P_Q均大于50%时说明渗漏风险较大，风险不可接受，需要开展第2层次风险评价.

(3)渗漏量和组分浓度的计算

渗漏风险评估模型由渗漏量和污染物组分浓度的确定性模型以及用于刻画模型参数不确定性的随机模型构成. 确定性模型中，渗漏量的计算包括地表降水、蒸发蒸腾、堆体入渗、导排层侧向排水以及通过粘土、土工膜的渗漏等多个地表和地下水文过程，计算方程和方程参数参见文献(Schroeder et al., 1994；Field and Nangunoori， 1993).

污染组分的浓度计算采用指数衰减源模型，参见文献(Walker，1993).

(4)渗漏概率计算

模型参数(降雨量、蒸发量等)的不确定性通常用概率密度函数(Probability Density Function，PDF)描述，而模型参数对渗漏概率则采用Monte Carlo算法来估计. Monte Carlo算法是目前解决风险评价中参数不确定性问题最为有效的方法之一(Denton et al., 2003). 其核心原理就是采用服从某种概率分布的大量随机抽样来模拟可能出现的结果及其概率分布(Dahlgren et al., 2003)，其计算流程见图 3. 假定目标函数Y满足

图 3(Fig. 3)

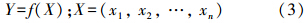
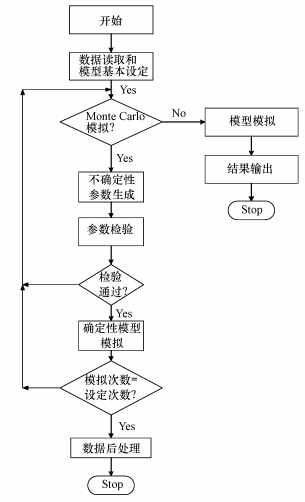图 3 Monte Carlo算法的基本流程 Fig. 3 Basic procedure of Monte Carlo Method

式中，x_i为服从某一概率分布的随机变量；f(X)为一复杂的函数关系式，用解析法难以求得Y的概率分布.

Monte Carlo模拟就是通过计算机随机抽样生成出每一随机变量的一个样本值，然后代入式(3)求出函数值Y，反复地独立模拟计算多次后得到函数Y的一组值Y_l，Y₂，…，Y_n. 当模拟的次数足够多时，就可由此来确定目标函数Y的概率特征.

(1)污染风险表征

定义地下水水污染风险为地下水中污染物浓度(C_wi)超过标准值的概率(P_p)，其中污染物浓度标准值取地下水三级质量标准中各污染组分的浓度限值，当超标概率P_P大于50%时认为风险较大，不可接受. 假设地下水三级质量标准中污染组分i的标准限值是CL_i，由第二层次风险评价模型计算得到地下水中污染组分i的浓度累计频率分布为F(C_wi)，则P_P可以通过下式计算：

(2)地下水污染物浓度计算

假设包气带和地下水中的水流运动均为一维的稳态水流，包气带中溶质运移服从一维的瞬态方程，含水层中溶质运移服从平面二维瞬态方程，考虑其吸附解析以及一级反应常数，其迁移平衡方程为:

式中， C_i和C_wi分别为目标污染组分i在包气带和地下水含水层中的浓度(mg · L^-1)；t为时间(d)；Z为包气带模型的深度坐标(向下为正)(m)；x和y为地下水含水层模型中的x和y坐标；v为渗滤液通过防渗层的渗漏速度(等于渗漏流量/填埋场库底面积)(cm · d^-1)；R为滞后因子，无量纲，取1；D 为包气带的水动力弥散系数(m² · d^-1)；K_i为污染组分i的一阶降解系数，无量纲；D_x和D_y分别为含水层中x、y 方向上的水动力弥散系数(m² · d^-1)；u_x为地下水流速(m · d^-1)；λ为一级反应常数(d^-1)； n₁为地下水含水层的孔隙度.

模型初始条件假设：浓度初值即为包气带和含水层中各污染组分的背景值，即：

式中，C_bi和C_wbi分别为包气带和含水层中污染组分i的背景值浓度(mg · L^-1).

模型边界条件：包气带上边界为给定浓度边界，下边界为零浓度梯度边界，即：

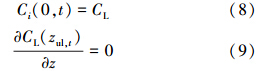
式中，z_ul为包气带底部的深度(m).

对于饱和带模型，其边界条件为：

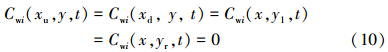
式中：x_u、x_d、y_l和y_r分别表示模型上、下游边界和左右边界.

本研究采用解析解法对上述方程求解见相关文献(王洪涛，2008)，并基于Matlab编制了其求解程序.

(3)污染物浓度的概率分布计算

与2.2.1(3)节类似，采用PDF函数表征地下水模型参数的不确定性，用Monte Carlo方法模拟参数不确定性对污染物浓度分布的影响.

第3层次评价为人体健康风险评价，采用剂量-效应模型，主要考虑人群通过饮用受渗滤液污染的地下水暴露的健康风险. 假设根据第2层次风险评价模型计算得到的地下水污染物的浓度分布，其健康风险可根据式(11)~(13)计算(陈鸿汉等，2006；李如忠，2007)：

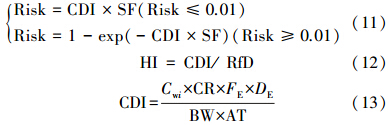
式中，Risk和HI分别为致癌风险值和非致癌风险值；SF为致癌斜率因子(mg · kg^-1 · d^-1)；CDI为长期日摄入剂量(mg · kg^-1 · d^-1)；RfD为非致癌参考剂量(mg · kg^-1 · d^-1)； CR为饮用水摄入速率(L · d^-1)；F_E为暴露频率(d · a^-1)；D_E为持续暴露时间(a)；BW为体质量(kg)；AT为平均时间(对致癌物质取人类平均寿命70a共有的天数(郑德凤，2008)；对非致癌物质取DE和FE的乘积，即将危害平均到整个暴露作用期)(d).

当致癌风险值大于10^-6或非致癌危害商大于1时，认为对人体健康影响较大，为不可接受风险(Li et al., 2007；Hu et al., 2013).

计算结果的可信度与模型模拟次数有关，可信度可用置信水平(Confidence Level)来表示，可信度与模拟次数之间的关系可用式(14)表示. 文献研究(Slack et al., 2007)表明当置信水平大于95%时结果具有较好的稳定性. 本文选择了CF=99%. 并根据公式(14)，反推了需要进行的模拟次数为1001次.

选择西北地区某非正规填埋场进行案例分析. 该填埋场采用粘土加单层HDPE膜防渗，但未建设渗滤液导排系统，不符合工业固体废物填埋标准设计填埋场，且在建设前没有进行详细的水文地质勘探，属于非正规填埋场. 该填埋场主要用于填埋场经湿法解毒+固化工艺进行解毒后的铬渣，总计填埋场量为8.92万t. 填埋场所在区域为属暖温带大陆性气候，多年平均气温10.5 ℃，多年平均降水量522.5 mm.

填埋场渗滤液渗漏后进入地下水，并顺着地下水流方向迁移，进入填埋场南侧1600 m处的河流中，因此假设暴露距离为1600 m，人群通过饮用此处地下水产生健康风险.

第1层次风险评价所需参数中降雨量服从参数为(456.6±83.5)mm的正态分布，总铬浓度和六价铬浓度分别服从参数为(2.74±3.29)和(2.07±2.89)mg · L^-1的对数正态分布，防渗膜上漏洞密度取24 个· hm^-2. 填埋场结构相关参数及其概率分布如表 1所示.

表 1(Table 1)

表 1 第1层次风险评价所需主要参数 Table 1 Main parameters of the first level risk assessment

表 1 第1层次风险评价所需主要参数 Table 1 Main parameters of the first level risk assessment 填埋场结构 厚度/cm 孔隙度 饱和渗透系数/(cm·s-1) 田间含水率 注：C表示常量(Constant)；N表示正态分布(Normal). 覆盖层 表层黄土 50 N 46%±2% C 6.4×10-5 C 31% 煤矸石 2000 C 39.7 C0.2 ± 0.1 C 3.2% 压实黄土 150 N 43.7%±1.6% C 3.6×10-6 C 37.3% HDPE 0.05 / C 1.0×10-13 / 土工布 0.2 / C 1.0×10-8 / 压实粘土 100 N 47.5%±1.6% N(1.7±0.6)×10-7 N 37.8%±1.2% 填埋层 解毒铬渣 300 N 0.63%±0.6% C 2.0×10-6 N 23.4%±5.4% 防渗层 压实粘土 100 N 47.5±1.6 N(1.7±0.6)×10-7 N 37.8%±1.2% 土工布 0.2 / C 1.0×10-8 / HDPE 0.05 / C 1.0×10-13 / 土工布 0.2 / C 1.0×10-8 / 压实黄土 100 N 43.7%±1.6% C 3.6×10-6 C 37.3%

第2层次风险评价所需参数主要为渗流和污染物运移相关的多孔介质参数，其取值见表 2.

表 2(Table 2)

表 2 第二层次风险评价所需参数 Table 2 Main parameters of the second level of RA

表 2 第二层次风险评价所需参数 Table 2 Main parameters of the second level of RA 参数 取值 包气带 厚度/m 渗透系数/(cm·s-1) 纵向弥散度 m C 5 logN(1.9±1.6)×10-5 含水层 厚度/m 水力坡度 纵向弥散度/m 横向弥散度/m 渗透系数/(cm·s-1) C 10 C 0.05 N(40.0±2.6)×10-5

第3层次风险评价所需参数主要为人体暴露参数，其取值见表 3.

表 3(Table 3)

表 3 第三层次风险评价所需参数 Table 3 Main parameters of the third level of RA

表 3 第三层次风险评价所需参数 Table 3 Main parameters of the third level of RA 参数名称 单位 取值 饮用水摄入速率(CR) L·d-1 2 暴露频率(FE) d·a-1 365 持续暴露时间(DE) a 24 人体质量(BW) kg 60 致癌效应平均时间(AT) d 26280 RfD 总Cr mg·kg-1·d-1 3 六价Cr 2×10-2

随机模拟1001次后得到第1层次风险评价模型的年平均渗漏强度的历时曲线如图 4a所示. 渗漏量的90%和95%分位值在300年左右达到峰值，5%、10%和50%分位值在1000年左右达到峰值. 因此，分别绘制第30、300和1000年年渗漏强度的累计频率曲线如图 4b所示. 根据2.2.1(1)节计算得到该填埋场可接受的渗漏强度为233 L · d^-1，根据式(4)，结合图 4b计算得到第30、300和1000年，其渗漏强度的超标概率均为0.

图 4(Fig. 4)

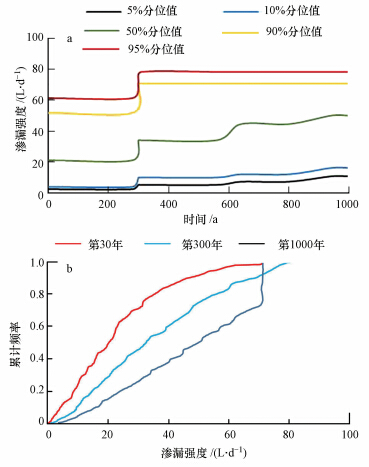图 4 渗漏强度的历时曲线和累计频率曲线(a：历时曲线；b：累计频率曲线) Fig. 4 Duration curve and cumulative frequency curve of leachate leakage rate(a：Duration curve；b：cumulative frequency curve)

由第2层次风险评价模型计算得到目标点处污染物浓度的历时曲线如图 5所示. 从图中可知观测井中污染物浓度在第9年达到峰值. 因此取9年的污染物浓度的概率分布作为地下水污染风险评价的依据，从图中可知观测井中总铬浓度和六价铬浓度超过地下水三级质量标准限值(1.5和0.05 mg · L^-1)的概率均为0.

图 5(Fig. 5)

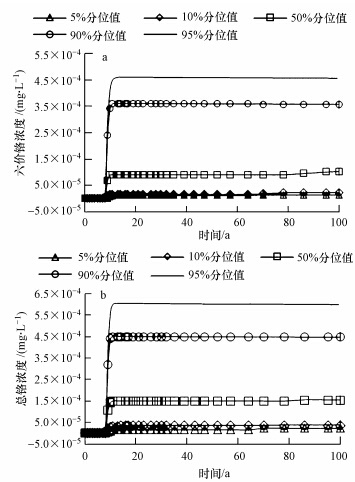图 5 暴露点污染组分随时间的变化 Fig. 5 Concentration of contaminants as a function of time

假设1600 m污染物的峰值浓度为人群的暴露浓度，代入式(11)~(13)计算得到总铬和六价铬的非致癌危害商，见图 6. 从图中可以看出总铬和六价铬的非致癌危害商均在10^-3~10^-2数量级左右，明显小于可接受风险水平.

图 6(Fig. 6)

图 6 暴露浓度及非致癌危害商的累计频率分布 Fig. 6 Cumulative frequency distribution of exposure concentration and HI

采用美国环保署开发的渗滤液迁移转化复合模型(EPA′s Composite Model for Leachate Migration with Transformation Products，EPACMTP)模拟渗滤液渗漏条件下的地下水污染，采用美国环保署推荐的健康风险评价模型计算地下水污染情况下的人体健康风险(不确定性参数采用其95%分位值，其他参数保持一致)，计算结果与本模型模拟结果的比较见表 4. 从表中可以看出EPACMTP-健康风险评价模型的计算结果略小于本模型计算结果(95%分位值)，相对差值基本保持在18%以内，说明本模型计算结果基本可靠.

表 4(Table 4)

表 4 层次化风险评价模型与EPACMTP模型比较 Table 4 Comparison between this model and EPACMTP model

表 4 层次化风险评价模型与EPACMTP模型比较 Table 4 Comparison between this model and EPACMTP model 模型类型 污染物峰值浓度/(mg·L-1) 非致癌危害商(HI) 六价铬 总铬 六价铬 总铬 3级概率风险评价模型 5%分位值 0.2 0.1 1.1×10-4 2.0×10-4 50%分位值 0.8 1.3 1.0 ×10-3 1.6 ×10-3 95%分位值 4.0 5.8 4.1 ×10-3 6.0 ×10-3 EPACMTP-健康风险评价模型 3.2 5.1 3.3 ×10-3 5.3× 10-3 相对差值(与本模型的95%分位值比较) 10.0% 12.1% 17.1% 11.7%

根据第1层次风险评估结果，渗滤液年平均渗漏强度超过可接受渗漏强度的概率为0；渗滤液中污染组分浓度超过相应的污染物排放限值的概率为1，根据2.2.1(2)节判断渗漏风险很小，可以接受. 根据第2层次风险评估结果，地下水中污染组分(六价铬和总铬)的峰值浓度分别位于(9.0×10^-6，6.0×10^-4)mg · L^-1区间和(7.7×10^-6，8.2×10^-4)mg · L^-1区间，超过相应的地下水三级质量标准限值的概率为0，因此判断地下水污染风险很小，可以接受. 最后根据第三层次风险评估结果，六价铬和总铬的非致癌危害商分别位于(1.0×10^-4，6.7×10^-3)区间和(8.5×10^-6，9.2×10^-3)区间，可判断其健康风险处于可接受水平.

本案例中，第1、第2和第3层次的风险可接受情况如表 4所示. 显然，当第1层次的渗漏风险水平可以接受时，第2层次的地下水污染风险和第3层次的人体健康风险均处于可接受水平，这表明在对非正规填埋场进行风险评价时，可以采用层次化风险评价的思路，先进行初级的风险评估，当初级的风险评价结果不可接受时，才继续进行进一步的风险评价.

第1层次评价模型所需的参数主要为工程设计参数，均可通过设计资料获取，所需要的时间成本和工程成本极小；第2层次评价模型所需的参数主要为水文地质参数，需要通过水文地质勘探获取，时间成本和工程成本极高；第3层次评价模型除第1、第2层次所需的参数外，对填埋场周边进行社会经济条件调查也将产生一定的时间和工程成本. 本案例中，各层次风险评价所耗的时间成本和工程成本列于表 5.

表 5(Table 5)

表 5 各层次风险评价结果及其时间、工程成本 Table 5 Results and cost of the 1st，2nd and 3rd level of risk assessment

表 5 各层次风险评价结果及其时间、工程成本 Table 5 Results and cost of the 1st，2nd and 3rd level of risk assessment 风险评价模型 是否可接受 时间成本/d 工程成本/万元 累计成本/万元 第1层次 是 3 0.5 0.5 本模型 第2层次 是 60 11.5 12 第3层次 是 80 2 14 EPACMTP模型 是 80 14 14

根据层次化风险评价的理论，因为第1层次的渗漏风险很小本案例可无需进行后续的风险评价，从而节省第2层次和第3层次风险评价时水文地质勘探和社会条件调查所需的大量时间成本(95%)和工程成本(96%).

1)从评价效果考虑，第1层次的风险评估结果能较好的表征第2层次和第3层次风险的大小，因此可作为是否进行后续风险评价的判断依据.

2)从时间成本和经济成本考虑，采用层次化的风险评价模型有助于大幅降低风险评价的时间成本和经济成本. 考虑到ISWL的特殊性(数量多且基本水文地质资料不详)，层次化风险评价模型的实践意义和经济意义更是非同一般. 仅就本填埋场而言，若采用层次化风险评价模型，可节省95%的时间(57 d)和96.5%的工程成本(13.5万元).

3)案例研究表明：①该填埋场渗漏量超过可接受渗漏量的概率为0，渗漏风险极小；②渗滤液的渗漏对地下水影响很小，污染风险为0；③该填埋场渗滤液中存在的六价铬和总铬的非致癌危害商在(1.0×10^-4，6.7×10^-3)区间和(8.5×10^-6，9.2×10^-3)区间，健康风险水平很小；④该ISWL的环境风险较小，无需采取工程措施对其进行治理或搬迁.