南水北调东线工程是利用江苏省已有的长江水北调工程，从长江下游的江苏省江都市抽引长江水，利用京杭大运河及与其平行的河道逐级提水北送，并连接起调蓄作用的洪泽湖、骆马湖、南四湖、东平湖.南水北调东线源头水质的好坏直接影响到水资源使用价值和沿线地区经济和社会的发展，决定着南水北调工程的实际效益，同时也将对输水沿线水环境产生重要影响.水质评价是以定量的方式直观表征水环境的质量状况，是根据国家相关的水质标准，运用有效的水质评价方法，给出被评价水体的当前水质状态，以及发展趋势.通过水质评价可以了解水环境质量的过去、现在和将来发展趋势及其变化规律，从而为水环境质量的科学管理和规划提供科学依据(Huang et al., 2001).

近年来，水质评价一直是人们探讨的热点问题，国内外学者对水质评价方法进行了许多有益的研究，相继提出了模糊综合评价法、灰色关联法、主成分法、神经网络法、支持向量机法、遗传算法等多种水质评价方法(王群妹等，2010；翟俊等，2007；潘妮等，2008；余勋等，2013；李雪等，2010;马文涛，2007；周荣喜等，2013；尹海龙等，2008；郑巧仙等，2011；龚艳冰等，2011)，这些方法都各有特点，尹海龙等(2008)对上述典型的7种河流综合水质评价方法的优缺点进行了比较研究.事实上，水质评价的实质是如何确定各评价指标的权重问题，而水质状态与各评价指标间是一种非常复杂的非线性关系.南水北调东线源头的水质优劣情况及对它的评价对于整个工程项目的顺利进行有着非常重要的意义.同时，由于分形理论在处理复杂的非线性现象和规律上具有突出优势.因此，本文试图构建基于分形维数权重的水质评价模型，并以长江江都市芒稻河断面2001—2008年的年平均水质监测数据为例对模型进行验证，以期从新的角度探索东线源头的水质评价方法.

分形的概念最早是由美籍数学家曼德布罗特(Mandelbort， 1975)提出的，分形维数作为分形的定量表征和基本参数，是分形理论的重要原则.而分形理论是描述自然界中许多不规则事物的规律性科学，它使得人们能够以新的概念来处理非线性领域中的问题，揭示复杂现象背后的规律、局部和整体之间的本质的内在关联性.分形特征的度量通常用分形维数(Fractal dimension)来表示，本研究中分形维数权重的确定步骤如下(刘光萍等，2005；王威等，2011).

假设江都市芒稻河断面水质评价影响因素中第i个指标X^*_i的数据向量为：

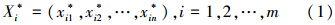
式中，n为待评价因素的样本个数；m为待评价对象的指标个数.

1)对数据进行规范化处理，对于效益型指标和成本型指标分别按式(2)和(3)进行计算，之后将指标变换到[0，1]区间，即得到数据归一化后的指标数据向量如式(4)所示.

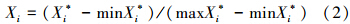
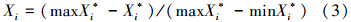
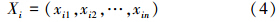
2)建立1~7维相空间(需要时可多达9维或更大)，形式如下：

3)分别计算上述1~7维相空间两点之间的距离r_pq(s)与平均距离Δx_s，计算公式为：

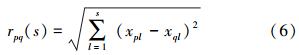
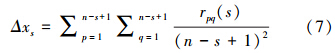
式中，p，q=1，2，…，n-s+1(不同相空间的点数)；s=1，2，…，ω(相空间维数ω=7).

4)分别计算上述1~7维相空间两点之间距离小于r_sk的概率C_k(s)，计算公式为：

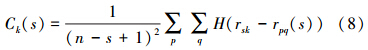
式中，r_sk为指定的距离上限，k一般取相空间维数ω的2倍，H为Heaviside函数，其值分别由下式确定：

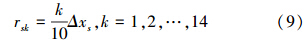
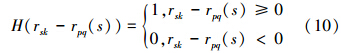
5)如果存在分形，则每维相空间有：

根据上述1~7维相空间求出一组C_k(s)值，在C_k(s)和r_sk双对数图上若为直线，则分形存在，其斜率为分形维数，即：

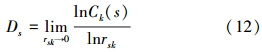
6)若分形维数随着相空间维数的升高趋向极限，则此极限值为空间的分形维数.在实际应用中，若分形维数没有严格地趋向某一极限，则采取比较不同维数相空间的分形维数，选择其趋于稳定的最大者或相邻空间分形维数之差满足一定精度，作为该水质评价影响指标的分形维数.

依据上述方法求出每个水质评价影响指标的分形维数权重，可根据如下步骤建立水质评价分形插值评价模型.

1)对影响水质状况的各评价指标进行数据归一化预处理，从而消除指标的量纲并统一指标的变化方向.

2)在上述评价标准等级范围内，利用Matlab软件按均匀分布随机产生l个标准样本，对于每个指标采用同一组随机数值，若有T个评价标准等级，则可形成l × T个评价标准样本，每个评价样本对应的经验等级为y(j).

3)根据公式(6)~(12)计算各指标分形维数D_i，利用公式(13)可求得第j个样本的评价值.

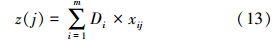
4)对于T个评价等级，设第t个评价等级对应的评价值z(j)∈[S_t，S^t]，其中，S_t、S^t是根据国家《地表水环境质量标准》(GB3838—2002)确定的5类水质分类区间的上界和下界，根据第j个样本计算的评价值z(j)与经验等级y(j)(式(14))，建立z(j)-y(j)的散点图，根据散点图可建立相应的分形插值评价模型(阶梯函数).

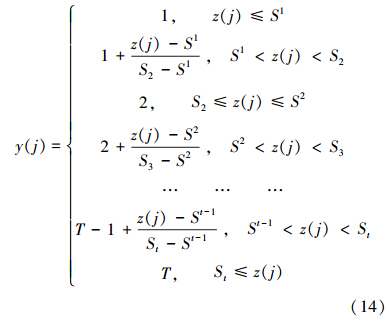
2002年，国家环境保护总局、国家质量监督检测检疫总局共同发布了《地表水环境质量标准》(GB 3838—2002)，标准依据地表水水域环境功能和保护目标，按功能高低依次划分为5类，对应地表水5类水域功能.地表水环境质量标准基本项目标准分为5类，不同功能类别分别执行相应类别的标准值，水域功能类别高的标准值严于水域功能类别低的标准值(龚艳冰等，2011).

根据江苏省江都市地区的水质实际情况，本文选取《地表水环境质量标准》(GB 3838—2002)中部分指标体系，分别是BOD₅(x₁)、溶解氧(x₂)、氨氮NH₃-N(x₃)、高锰酸盐指数(x₄)、石油类(x₅)、粪大肠菌群(x₆)、挥发酚(x₇)，其中，溶解氧是效益型指标，其他都为成本型指标.将水质等级划分为5个等级，各评价指标与水质等级的关系如表 1所示.

表 1(Table 1)

表 1 不同水质等级的评价指标值 Table 1 Environmental quality Standards for different evaluation indexs of surface water

表 1 不同水质等级的评价指标值 Table 1 Environmental quality Standards for different evaluation indexs of surface water 水质等级 BOD5/(mg·L-1) 溶解氧/(mg·L-1) 氨氮/(mg·L-1) 高锰酸盐指数/(mg·L-1) 石油类/(mg·L-1) 粪大肠菌群/(个·L-1) 挥发酚/(mg·L-1) Ⅰ类 0~3 7.5~10 0~0.15 0~2 0~0.05 0~200 0~0.002 Ⅱ类 0~3 6~7.5 0.15~0.5 2~4 0~0.05 200~2000 0~0.002 Ⅲ类 3~4 5~6 0.5~1.0 4~6 0~0.05 2000~10000 0.002~0.005 Ⅳ类 4~6 3~5 1.0~1.5 6~10 0.05~0.5 10000~20000 0.005~0.01 Ⅴ类 6~10 2~3 1.5~2.0 10~15 0.5~1.0 20000~40000 0.01~0.1

在上述各评价标准等级范围内按均匀分布随机产生10个样本，对于每个指标采用同一组随机数值，共形成50个评价样本，将Ⅰ~Ⅳ类水体和Ⅴ类水体分别赋予经验等级1~5共5个等级，结果如表 2所示.

表 2(Table 2)

表 2 预处理后的标准样本 Table 2 Standard sample pretreatment

表 2 预处理后的标准样本 Table 2 Standard sample pretreatment 序号 BOD5 溶解氧 氨氮 高锰酸盐指数 石油类 粪大肠菌群 挥发酚 等级 1 0.1546 0.1288 0.0010 0.0087 0.0326 0.0000 0.0003 1 2 0.1142 0.0688 0.0435 0.0983 0.0396 0.0011 0.0056 1 … … … … … … … … … 11 0.1818 0.4756 0.1733 0.1969 0.0386 0.0253 0.0178 2 12 0.0993 0.4092 0.1916 0.2488 0.0224 0.0097 0.0045 2 … … … … … … … … … 21 0.3967 0.5932 0.3636 0.3978 0.0053 0.0891 0.0429 3 22 0.3504 0.5247 0.4192 0.3988 0.0262 0.0783 0.0473 3 … … … … … … … … … 31 0.5644 0.6742 0.7262 0.6460 0.0505 0.4468 0.0954 4 32 0.5129 0.7572 0.7356 0.5344 0.1272 0.3642 0.0504 4 … … … … … … … … … 49 0.9482 0.8806 0.8368 0.8055 0.6264 0.9164 0.5102 5 50 0.8624 0.9716 0.8582 0.7752 0.7287 0.6868 0.6264 5

根据公式(6)~(12)利用Matlab软件编程，计算水质评价指标X=(x₁，x₂，x₃， x₄， x₅， x₆，x₇)的分形维数D=(1.4939，1.4499，1.1465，1.3578，0.3960，0.7784，0.3342).图 1为利用表 2样本数据建立7维各指标的相空间，拟合出的影响指标x₁的对数lnC_k(s)-lnr_sk曲线，曲线的斜率就是所要求的关联分形维数权重(限于篇幅，仅给出1维和7维相空间的拟合曲线)，其他6个影响指标可以采用相同的方法求得.

图 1(Fig. 1)

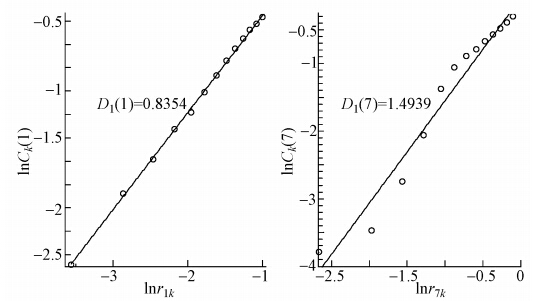图 1 水质评价指标x1的lnCk(s)-lnrsk拟合直线 Fig. 1 Line fitting(lnCk(s)-lnrsk)of water quality evaluation index x1

根据公式(9)算出的上述50个样本的综合评价值分别如下：

以经验等级值为纵坐标，以综合评价值为横坐标，得到两者的散点图(图 2).从图 2可以看出，z(j)和y(j)的图形为阶梯形、上升曲线，根据公式(13)用a、b、c、d、e、f、g、h、k、l分段线性插值，得到水质评价的分形插值等级模型(分段函数)，具体见公式(15).

图 2(Fig. 2)

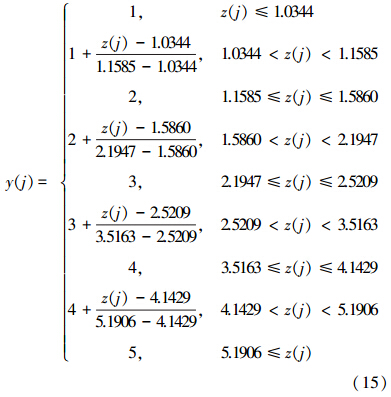
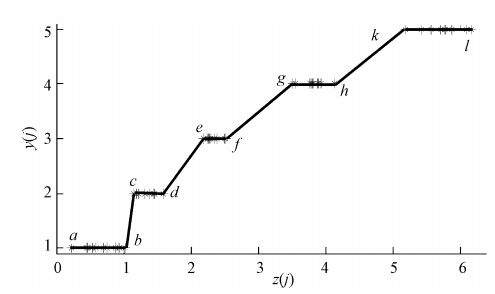图 2 综合评价值与经验等级值的散点图 Fig. 2 Scatter plot of comprehensive evaluation and experience level value

根据《地表水环境质量标准》(GB3838—2002)和扬州市江都环境监测中心站的原始数据，本文收集了南水北调扬州江都芒稻河地区从2001—2008年比较完整的数据：长江芒稻河二水厂断面为BOD₅、挥发酚、溶解氧、石油类、氨氮、高猛酸盐指数、粪大肠菌群共7个水质指标的数据(梁雪春等，2010)，具体如表 3所示.

表 3(Table 3)

表 3 芒稻河二水厂断面主要监测指标的年平均值监测值 Table 3 Average annual monitoring values of Mangdaohe section in second water plant

表 3 芒稻河二水厂断面主要监测指标的年平均值监测值 Table 3 Average annual monitoring values of Mangdaohe section in second water plant 年份 BOD5/(mg·L-1) 溶解氧/(mg·L-1) 氨氮/(mg·L-1) 高锰酸盐指数/(mg·L-1) 石油类/(mg·L-1) 粪大肠菌群/(个·L-1) 挥发酚/(mg·L-1) 2001 1.575 6.8 0.330 3.638 0.01775 1175 0.001 2002 1.125 6.7 0.451 3.242 0.055 2483 0.001 2003 1.675 7.2 0.441 3.375 0.020 1900 0.001 2004 1.700 7.9 0.284 3.050 0.033 1683 0.002 2005 1.575 7.8 0.374 2.900 0.050 2116 0.002 2006 1.930 7.3 0.420 3.383 0.050 1974 0.002 2007 2.067 6.9 0.468 3.633 0.083 1766 0.002 2008 2.067 7.7 0.394 3.325 0.100 2520 0.002

将表 3的数据规范化后代入线性插值公式(15)，得到芒稻河二水厂断面年平均水质的综合评价值，表 4是将本文方法与全排列多边形图示法(龚艳冰等，2011)及LM-BP网络法(夏美娟等，2011)进行综合比较的结果，图 3则反映了3种方法对该区域历年水质与Ⅰ类水体和Ⅱ类水体之间的关系，以及历年水质综合指数的总体趋势.

表 4(Table 4)

表 4 芒稻河二水厂断面水质评价方法结果对照表 Table 4 Comparison of water quality evaluation results of Mangdaohe section in second water plant

表 4 芒稻河二水厂断面水质评价方法结果对照表 Table 4 Comparison of water quality evaluation results of Mangdaohe section in second water plant 年份 分形维数权重法 全排列多边形图示法 LM-BP网络法 综合指标值 水质评价等级 综合指标值 水质评价等级 综合指标值 水质评价等级 2001 1.0370 [Ⅱ类，Ⅰ类] 0.4294 Ⅰ类 1.8599 Ⅱ类 2002 1.3916 Ⅱ类 0.2272 Ⅱ类，Ⅰ类 1.6665 Ⅱ类 2003 1.3642 Ⅱ类 0.3669 Ⅱ类，Ⅰ类 1.7055 Ⅱ类 2004 1.1260 Ⅱ类，Ⅰ类 0.5046 Ⅰ类 1.5799 Ⅱ类 2005 1.1786 Ⅱ类 0.2564 Ⅱ类，Ⅰ类 1.4408 Ⅱ类 2006 1.3896 Ⅱ类 0.1585 Ⅱ类，Ⅰ类 1.6842 Ⅱ类 2007 1.5417 Ⅱ类 0.0745 Ⅱ类，Ⅰ类 1.8529 Ⅱ类 2008 1.3478 Ⅱ类 0.0889 Ⅱ类，Ⅰ类 1.8235 Ⅱ类

图 3(Fig. 3)

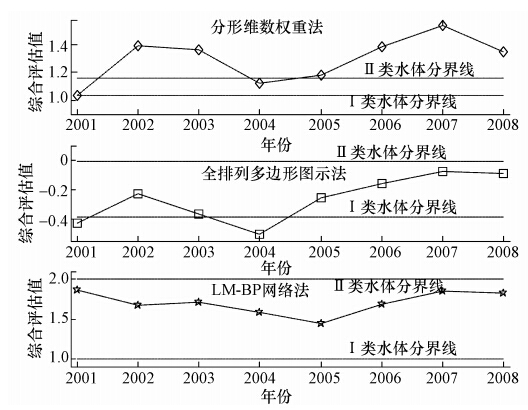图 3 芒稻河断面年平均水质分类及趋势(为了便于比较趋势，全排列多边形图示法的综合指标值取负号) Fig. 3 Average annual water quality classification and trends in Mangdaohe section

由表 4可以看出，全排列多边形图示法得到的水质评价等级过于乐观，LM-BP网络法的水质评价等级过于保守，分形维数权重法介于两者之间.这是因为全排列多边形图示法虽然简洁直观，能够反映系统的整合原理，评价结果也有较明确的几何意义，但这种方法没有考虑各影响因素之间的权重，是一种等权的评价方法.LM-BP网络法虽然考虑了权重因素的影响，但由于在算法运行过程中需要一定数目的训练样本，如果训练样本的数目比较少，则水质评价结果会趋于保守.分形插值方法既考虑了指标间的非线性关系又考虑了指标间的权重关系，不会过分依赖于训练样本数，因此，评价结果更合理、客观.同时，从图 3可以看出，分形维数权重法得到的Ⅰ类水体与Ⅱ类水体分界线之间的距离要比另外两种方法小，这是因为水质达到优良的难度是呈非线性增大的，反映了达到Ⅰ类水体目标的难度在不断增加，这与《地表水环境质量标准》的分类等级中Ⅰ类水体与Ⅱ类水体分界值是一致的.

水质评价是一个复杂的非线性系统问题，本文利用分形理论较强的非线性数据处理能力，构建了基于分形维数权重的水质评价模型，该模型针对标准样本量少的问题，可以在每级标准之间随机内插构建标准样本集.此外，利用该模型可以得到一个具体的数值，不但能评价水质的等级，而且还能对同等级水质进行排序，因而具有较高的分类精度.从评价结果来看，南水北调东线源头地表水环境质量总体良好，江都段历年水质都保持在Ⅱ类水体标准以上，基本达到可直接饮用的南水北调工程的要求.从2001—2008年长江芒稻河二水厂断面水质数据综合评估的结果可以发现，2007年其水质最差，2001年水质最好，而水质最差的3年也主要集中在2005年以后的年份.