随着气候条件日益干旱，城市化进程加快，导致水资源短缺、水质下降已是不争的问题.尤其在半干旱地区日照丰富、降水量少，水资源供需更加紧张，严重制约经济发展和人民生活质量(程磊等，2009).北京属于半干旱半湿润地区，降水年内、年际分布不均，春旱时有发生.且地下水位近年来持续下降(http://szyj.bjyq.gov.cn/gcjg/gcgh/143.html).另外官厅水库作为北京市重要供水水源之一，由于严重污染，于1997年被迫退出城市生活饮用水体系，导致北京市水资源短缺问题更加严峻.官厅水库重新启用对缓解北京市水资源现状具有重要意义，其水资源规划治理迫在眉睫.延庆妫水河流域是官厅水库的主要入库河流之一，其水质的好坏直接关系到官厅水库的水质状况.该地区开展了较丰富的地下水基础性研究，植物生态研究集中在生态监测及遥感技术支持的植被演替研究两方面.宫兆宁(2007)基于遥感和GIS，研究了该区湿地景观的演变趋势及其演变原因；丁连靖等(2007)从地面沉降原因、地震发生的机理等方面，客观地分析了地热开发与地表环境的关系.崔天翔等(2013)探讨了该地区不同端元模型下植被覆盖度的提取方法.然而，基于区域尺度的水文过程研究目前还鲜有开展.

流域水文模拟具有成本低、便于情景分析等优点，是水文分析计算、洪枯水预报、水资源管理与决策、生态保护的重要手段，具有广阔的应用前景(罗定贵等，2007).水文模型是描述和反映自然界中复杂水文现象的一个手段，是定量模拟水文现象特征量及其过程变化的一种有效工具(张哲，2007).HSPF(Hydrological Simulation Program-FORTRAN)模型源于 1966 年 SWM(Stanford Watershed Model)斯坦福模型，是一种半分布式模型，将数学方法应用于水文计算和预报形成的流域水文模型(Bicknell et al., 2001).该模型主要应用于水文和水质模拟，主要包括气候和土地利用变化对径流量的影响(Gncü et al.， 2010)、点源非点源污染研究(邢可霞等，2005).目前，HSPF模型内嵌于基于GIS的BASINS系统中，方便地形、土地利用、土壤等输入数据的叠加，同时延长了模拟预测的时间序列长度(Bicknell et al., 2001; 董延军等，2009).

传统的参数识别主要基于优化思想的参数识别思路，旨在发现一个最优参数组合反映研究区的水文过程，但由于水文系统的复杂性、参数间的相关性等问题，水文模型中会出现“异参同效”现象，从而导致水文模拟和预测过程的不确定性(李胜和梁忠民，2006; 梁忠民等，2009).分析水文模型参数不确定性的方法众多，主要有GLUE(Generalized likelihood uncertainty analysis)方法、经典贝叶斯法 、SUFI方法等，其中GLUE方法简单、易行、有效(Vrugt et al., 2009). GLUE方法由Beven and Binley 1992年提出，代表了水文模型不确定性研究领域的最新进展(戴健男等，2011).已被国内外水文学家应用于几种流域水文模型和很多流域之中(Beven and Binley， 1992; 黄国如和解河海，2007).Mcmichael等(2006)将该方法应用于美国加利福尼亚流域，分析MIKESHE模型参数不确定性；Xie and Lian(2013)应用该方法对比分析SWAT模型和HSPF模型在伊利诺斯河流域的不确定性；刘丽芳等(2013)将GLUE方法应用于HIMS模型，探讨澳大利亚3个流域的不确定性，对无资料区水文预报具有重要意义；此外该方法还应用于TOPMODEL、HIMS、新安江等模型.相比较而言，目前关于HSPF水文模型的不确定性研究还不深入，有待进一步研究.

本文建立了半干旱半湿润地区北京市延庆县妫水河流域的HSPF模型，选取该区东大桥水文站2005至2008年月径流数据进行该区水文模拟，并运行GLUE方法，研究该模型参数的不确定问题，分析模型参数的敏感性、参数间相关性、“异参同效”现象及模型预报的不确定性范围，为HSPF模型在该区水文预测等提供参考和依据.

妫水河流域位于北京市西北部，南、北、东三面环山，西面邻水的小盆地，是首都北京西北重要的生态屏障.妫水河流域地处延庆县属于永定河水系，地势东北高，西南低，自东向西注入官厅水库.本文研究区选自东大桥水文站以上流域，面积678 km²，海拔474~2218 m(图 1).地理坐标为40°22′8″~ 40°38′35″N，115°49′12″~116°20′35″E.东大桥水文站(30707200)位于延庆县延庆镇石河营村，属于区域代表站等级，高程为 480.15 m.

图 1(Fig. 1)

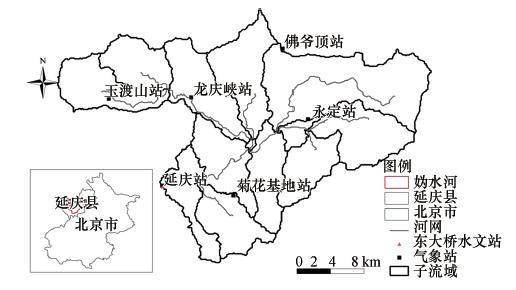图 1 研究区子流域、河网及气象水文站点分布 Fig. 1 Subbasins and stream of study area and hydrological and weather station

研究区属大陆性季风气候，地处北温带，是温带与中温带、半干旱与半湿润的过渡地带.径流主要依靠降雨和地下水补给，多年平均气温10 ℃左右，多年平均降水 400 mm左右，年最大降水 523 mm，且降水多集中在 5—8 月份.研究区主要为山前的洪冲积扇，是联系妫水河平原人工-半人工生态系统和周围森林自然生态系统的过渡地区，即典型的生态过渡带，是物质、能量、信息交流的界面，也是受到人为干扰较为强烈的地区，同时也是流域周边自然生态系统抵抗人为干扰的重要防线，是妫水河流域的生态敏感区和生态安全带(蔡博峰等，2006).土地利用类型以旱田和林地为主，林地主要沿研究区边界分布，旱田则主要分布在中部地区.土壤类型以褐土为主，分布在区内大部分地区，西北部山区多为棕壤，潮土则主要沿河分布.

HSPF模型对降雨径流的描述是最为复杂完善的，较好地再现了流域的降雨径流过程，为模型的后续模拟提供了良好的基础，模型模拟水文循环过程主要包括降雨、植被截留、地面径流、土壤水分配、蒸散发等部分(图 2)(Bicknell et al., 2001; 梅立永等，2007).HSPF主要通过透水地段水文水质模拟模块(PERLND)、不透水地段水文水质模拟模块(IMPLND)以及地表水体模拟模块(RCHRES)3个主模块模拟流域水文过程.其中透水地段在降雨满足截留、填洼和下渗时，剩余部分成为地面径流，其主要过程包括地表径流、坡面漫流、壤中流、地下径流和蒸散发；不透水地段降雨主要形成地表径流并耗于蒸散发；地表水体模拟主要指河流、水库的模拟，该模块主要包括降雨和蒸散发过程.

图 2(Fig. 2)

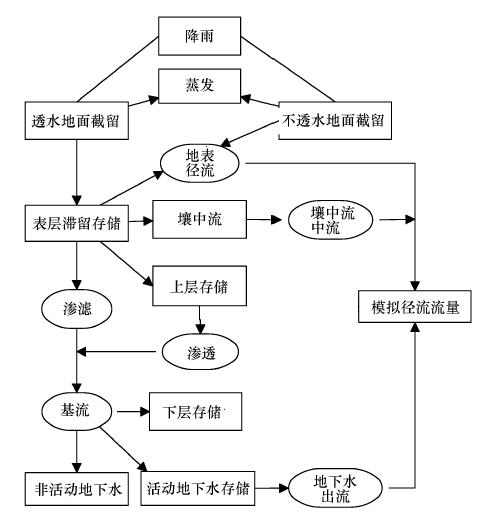图 2 HSPF水文模拟流程图(梅立永等，2007) Fig. 2 Flow Program for Hydrologic Module in HSPF(Mei et al.2007)

土地利用数据：结合研究区已有的1998年土地利用类型，通过ArcGIS软件对该区2005年TM影像数据进行人工解译得到林地、耕地、草地、城镇用地、水域、滩地6种土地利用类型.

气象数据：研究区均匀分布延庆、永宁等6个气象站(图 1)，包含2005—2008年逐日气温、降水、蒸发皿蒸发、日照时数、相对湿度、风速、气压等气象数据.

水文数据：研究包含东大桥1个水文站(图 1)，选取该站2005—2008年月径流数据进行水文模拟，其中2005年为预热期，2006—2007年为率定期，2008年为验证期.

PEST(Parameter Estimation)由John Doherty博士开发，是独立的参数估计软件，通过文件输入、输出与用户交互.PEST基于列文伯格-马夸尔特(Levenberg-Marquardt)算法，能够较少的运行模型且更高效的使目标函数收敛，得到最优参数，但该算法对模型初始参数具有较大依赖性(Doherty，2005).考虑到PEST算法对模型初始参数要求较高，研究结合人工率定和PEST率定程序对模型参数优选，通过人工率定得到合适参数初值，然后利用PEST自动率定程序得到最终参数.

PEST基于非线性算法以较少的循环次数优化目标函数，目标函数选取模型模拟值和观测值的差异函数.用式(1)表示参数与观测值的非线性关系：

式中，x为参数组；y为观测值；T为参数与观测值的非线性关系.

将式(1)线性化得式(2)：

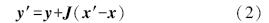
式中，x′和y′ 分别是参数与模型结果的矩阵. J 为雅可比偏导数矩阵，由式(3)求得:

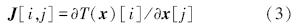
式中，i，j分别是 J 的行列数.每一次循环率定，PEST算法给参数矩阵 x′ 一个增量矩阵 u 循环更新:

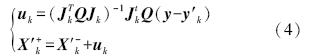
式中，k表示模型循环次数，上标“-”代表上次循环的参数矩阵，而“+”代表新一次循环即更新后的参数矩阵. Q 为观测值权重矩阵；由式(4)得目标函数(式(5)):

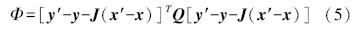
算法步骤：首先选定参数初值，存放在矩阵 x′ ₀中，然后对模型进行校正，将模拟结果存入矩阵 y′ ₀中，相对应的实际测量值存入矩阵 y 中；使用一阶泰勒展开式对 J ₀进行数值求解；应用式(4)计算参数增量矩阵u₀；在新的一次循环中用增量矩阵更新矩阵 x′⁺₁，并将x′⁺₁存入x′^-₁ 中，循环整个算法直到达到收敛.

但采用非线性方法当参数高度相关时，目标函数会出现“震荡”现象，收敛较慢.为了解决此问题，1963年Marquardt对通过增加参数λ对函数加以改进，，称为Levenberg-Marquardt算法，见式(6)：

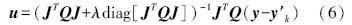
参数意义同上，改进算法结合梯度下降和牛顿方法以适应逆海森方法，当λ偏大时梯度下降法占优势，反之牛顿方法占优势.

GLUE方法认为对模拟结果影响的是参数组合而不是单一参数.GLUE方法首先确定每个参数的取值范围，并选取合适的似然函数；然后利用Monte-Carlo随机采样得到均匀分布的参数组并代入水文模型，生成相应的似然值；选取合适的似然函数临界值，把似然值分为有行为点和无行为点，即高于临界值的似然值是有行为点，其所对应的参数组合可以反映研究区的水文特征，无行为点则不能反映；对于有行为点的参数组似然值重新归一化，按照似然值的大小求出在某置信度下模型预报的不确定性范围(Beven and Binley， 1992; Li et al., 2010; Shen et al., 2012; Xie and Lian， 2013).

选取纳什系数Ens、确定性系数R²分别对校准期和验证期的月径流和年径流进行评价，计算公式如下：

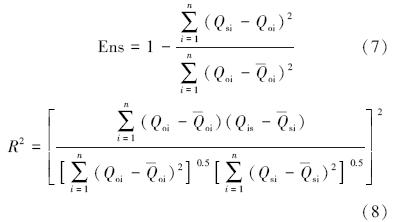
式中，Q_oi为实测月径流量(m³ · s^-1)；Q_si为模拟月径流量(m³ · s^-1)；Q_oi为模拟时段内平均实测月径流量(m³ · s^-1)；n为径流模拟的总月数.纳什系数Ens反映流量的拟合度，该值不大于1，当Ens>0.5时结果可接受.确定性系数R²是相关系数的平方，其取值为0~1，值越大表明模拟结果越好.

为了减少率定参数、提高模型运行效率，PEST程序自动筛选出敏感性排前10的参数进行率定.在本研究区筛选出的10个参数见表 1，与Doherty等(2003)和Singh等(2005)所选参数基本相同，但二者所选参数包括LZETP(下土壤层蒸发系数)，不包含参数CEPSC(植被截留系数)，而本文相反，是因为不同区域的水文特征及下垫面等情况不同，参数对不同流域的反应也不同，敏感性不同，故筛选出的敏感参数不尽相同.本研究人工率定和PEST自动率定结果及参数敏感性见表 1.人工率定结果为Ens= 0.47，R²=0.55，PEST自动率定程序结果为Ens=0.54，R²=0.59，PEST率定程序结果比人工率定结果还是优化很多.此外，通过表 1还可以看出参数敏感性大小，参数LZSN和AGWRC敏感性最高，敏感性是其他参数的5~2700倍；参数BASETP敏感性排第三，但敏感性明显比参数LZSN和AGWRC小很多，不足二者的1/5；其他参数敏感性则很小.

表1(Table 1)

表1 HSPF模型参数取值范围 Table 1 Ranges of HSPF parameters

表1 HSPF模型参数取值范围 Table 1 Ranges of HSPF parameters 参数名称 参数意义 取值范围 人工率定 PEST率定 敏感性 敏感性排序 LZSN 土壤下层额定存储量，其值是气候和土壤类型的函数. 2~15 5.20 4.60 27.82 1 UZSN 土壤上层额定存储量，与土壤表层特性和土地利用有关. 0.05~2 1.60 0.53 0.06 8 INFILT 土壤下渗系数，决定降水在地表、壤中流和地下水存储间的水量分配. 0.001~0.5 0.17 0.20 0.34 7 IRC 壤中流消退系数，是当前日壤中流出流与前一日壤中流出流的比率. 0.3~0.85 0.58 0.34 3.70 4 BASETP 基流蒸发系数，是基流补给河床时由河岸植被蒸发的水分. 0.001~0.2 0.080 0.15 5.15 3 AGWETP 潜水蒸发系数，表征直接由浅层地下水蒸发的水分占潜在蒸发量的比值. 0.001~0.2 0.050 0.16 0.01 10 AGWRC 地下水消退系数，是当前地下水流量和24小时前的流量的比值. 0.85~1 0.93 0.95 27.22 2 CEPSC 植被截留系数，是由植被截留降水并用于蒸发的非落地雨，参数可为月值. 0.01 ~0.4 0.20 0.070 1.80 5 INTFW 壤中流出流系数，通过分配壤中流和坡面流来影响径流时间. 1~10 4.40 7.10 0.040 9 DEEPFR 水分下渗到承压层的比率，值与地形和地下水补给有关. 0.001~0.5 0.030 0.010 1.60 6 Ens 纳什系数 — 0.47 0.54 — — R2 确定性系数 — 0.55 0.59 — —

本文率定期2006—2007年和验证期2008年月径流水文过程曲线见图 3，由图可知模拟曲线与观测曲线趋势基本一致，可合理反映研究区水文过程.

图 3(Fig. 3)

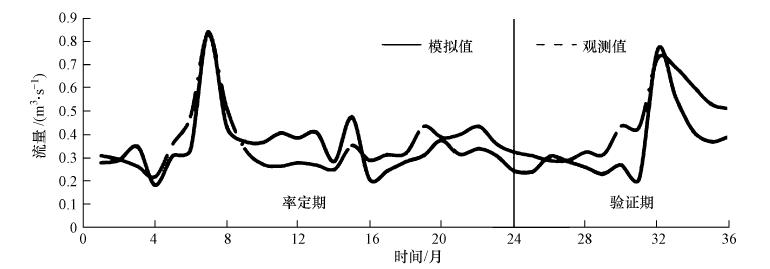图 3 率定期与验证期流量曲线 Fig. 3 Monthly flow curve of calibration year and validation year

以纳什系数作为似然目标函数，通过Monte-Carlo随机采样得到30000组参数进行不确定性分析.本文选取似然临界值为0.3(约2200组，占7.3%)，即低于0.3的参数组似然值赋为0，高于该值的似然值重新归一化并按似然值大小排序.下文的参数相关系数图(图 5)、预报不确定性(图 6)等均根据该临界值分析，但为了清晰、直观地反映参数与似然值的关系，二者散点图(图 4)选取临界值0.

图 4(Fig. 4)

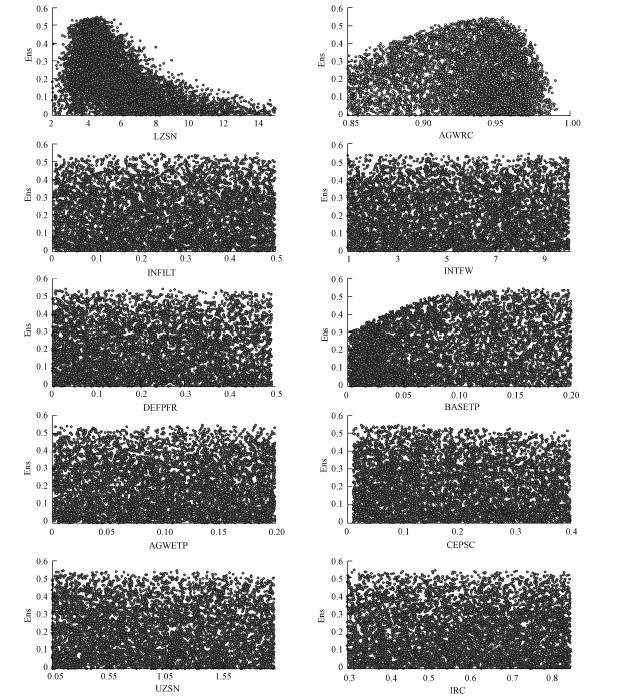图 4 参数似然散点图 Fig. 4 Scatter distribution of likelihood values of HSPF parameters

图 5(Fig. 5)

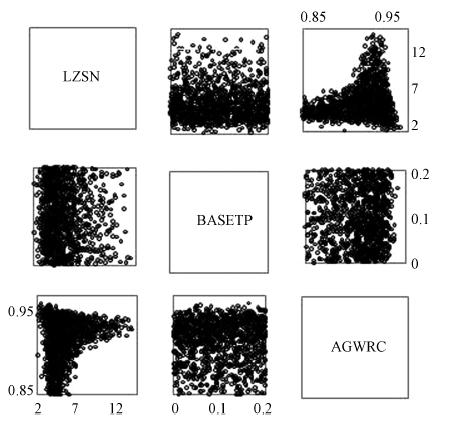图 5 参数相关性图 Fig. 5 Correlations between the sensitive parameters

图 6(Fig. 6)

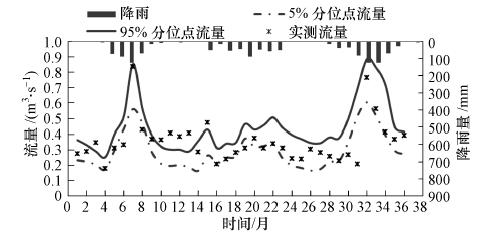图 6 研究区2006—2008年月径流模拟的不确定性范围 Fig. 6 Uncertainty ranges of the monthly runoff from 2006 to 2008 of Guishui River Basin

此处根据图 4分析参数敏感性，参数的敏感性与研究区、径流数据尺度(年或月或日)、目标函数和似然值等的选择有很大关系，不同的选择会得到不同的结果.Al-Abed和Whiteley(2002)应用HSPF模型模拟加拿大流域日径流数据，得到LZSN是最敏感参数；Doherty等(2004)在纽斯河流域建立HSPF日径流模型，通过PEST自动率定方法得到参数AGWRC和INFILT最为敏感；Iskrat和Droste(2007)中经分析发现参数INFILT 对日径流数据较敏感，而对月径流敏感的参数是AGWRC；本文得到对研究区月径流敏感的参数包括LZSN和AGWRC，区间敏感参数为BASETP，其他参数对月径流反应较小.

敏感参数：由图 4看出参数LZSN、AGWRC在整个取值区间都有较大变化且幅度较大，表明LZSN和AGWRC较为敏感，对不确定性影响较大.LZSN取0到3时，似然值随参数值的增大而增大，在3到6时达到稳定，6到15间随着参数的减小似然值减小.AGWRC在0.85至0.95间似然值随着参数的增大而增大，0.95至0.99间则相反，在0.99至1间没有点，原因在于参数值在0.99至1间时似然值为负.

区间敏感参数：参数BASETP则在一定区域内较为敏感，参数值在0至0.08间似然值随着参数值的增大而增大，在0.08至0.2间似然值趋于稳定.

不敏感参数：参数AGWETP、INFILT、CEPSC、DEEPFR、UZSN、INTFW、IRC则无变化趋势，表明对研究区的月径流量反应不敏感，对该区月径流量HSPF模型参数不确定性影响较小.

分析散点图得到LZSN、AGWRC和BASETP比较敏感，这与PEST自动率定程序得到的参数敏感性分析一致.根据散点图可以直观分析出参数具体在什么区间敏感、敏感性随参数变化怎么变化等问题；PEST程序可以定量分析出参数的敏感性大小，二者相互结合、相互补充.

目前多数不确定性分析方法都假定参数间是相互独立的，GLUE方法也是如此(Beven and Binley， 1992).然而，参数间的复杂相关性会导致参数冗余，是参数不确定性的因素之一.此处，针对较敏感的3个参数对应的可行参数组两两做散点图，得到三者相关性图(图 5)，由图知参数LZSN和AGWRC具有较大的相关性：参数AGWRC在0.85至0.95间与参数LZSN正相关，在0.95至1间则成负相关.参数LZSN和参数AGWRC的相关性也是不确定因素之一.

由于模型本身和观测资料的误差，通过观测数据率定出来的模型参数组合也存在一定偏差，它并不能代表一定模型参数下的“真实”参数值，而只是符合某一特定目标函数的似然估计的优化参数值，这样在参数空间就会存在“异参同效”现象，即不同的参数组合可得到相同的似然值(莫兴国和刘苏峡，2004).由图 4可看出“异参同效”现象非常普遍，证明了GLUE方法的观点：对模拟结果影响的不是单个参数，而是参数组合.

表 2列出了最大似然值的参数组，跨度是似然值为0.54时参数取值范围长度，空间长是参数本身的取值范围长度(见表 1)：比如参数LZSN的取值范围是2~15，则空间长就等于13；该参数在似然值为0.54时，最大值是4.860，最小值4.557，跨度就是二者之差，即0.303.百分比是跨度占空间长的百分比，百分比小意味着在高似然值区参数取值较为集中，也就是对应参数-似然值散点图“瘦尖”形状，也就是较敏感参数.由表知参数LZSN集中在4.5~4.9 之间和参数AGWRC集中在0.945左右，对应图 4散点图中最高区域，且二者百分比较小，即为敏感参数，与4.3节结果一致；参数BASTEP取值集中在0.14~0.19之间，与图 4结果也一致；其他参数跨度越大表明参数变化对似然值影响较小，也从另一方面说明跨度越大参数的敏感性也就较小.

表2(Table 2)

表2 异参同效参数组及各参数变化跨度 Table 2 Equivalent parameters of the study area and ranges of parameters

表2 异参同效参数组及各参数变化跨度 Table 2 Equivalent parameters of the study area and ranges of parameters 参数组 LZSN INFILT AGWRC DEEPFR BASETP AGWETP CEPSC UZSN INTFW IRC Ens 1组 4.727 0.284 0.947 0.018 0.192 0.067 0.075 0.683 2.749 0.437 0.54 2组 4.814 0.249 0.939 0.130 0.158 0.106 0.028 1.412 2.579 0.511 0.54 3组 4.557 0.216 0.948 0.079 0.169 0.013 0.085 0.616 1.898 0.614 0.54 4组 4.593 0.244 0.940 0.279 0.175 0.149 0.237 0.135 4.190 0.718 0.54 5组 4.860 0.215 0.944 0.031 0.157 0.135 0.024 1.146 4.368 0.517 0.54 6组 4.608 0.460 0.955 0.252 0.144 0.183 0.091 0.151 8.369 0.317 0.54 跨度 0.303 0.245 0.016 0.261 0.048 0.17 0.213 1.011 6.471 0.401 空间长 13 0.499 0.15 0.499 0.199 0.199 0.39 1.95 9 0.55 百分比 2.33% 49.10% 10.67% 52.30% 24.12% 85.43% 54.62% 51.85% 71.90% 72.91%

此处首先确定似然值(纳什系数)的临界值为0.3，选取高于该值的似然值并归一化，然后将模拟径流量按大小排序，估算出模型预报的不确定性时间序列.选用90%置信度下模型模拟的不确定性范围，即累计似然分布的5%和95%两个分位点作为预测不确定性的界限.图 6列出了2006—2008年月径流的不确定性范围.由图知不确定性范围与径流大小密切相关，径流大的地方不确定性范围大，径流小的地方不确定性范围小，图中不确定性范围包含了58.3%的观测值，属于可接受范围.但不确定性范围并没有包含所有观测值，表明模型并不能完全模拟出流域河道的径流过程，这一方面受研究区复杂水文过程的影响，另一方面似然值的临界值具有一定的主观性，不同的临界值会产生不同的不确定性范围.

1)HSPF模型参数中对研究区月径流敏感的参数包括LZSN和AGWRC，区间敏感参数为BASETP，其他参数对月径流反应较小.

2)文章研究参数间相关性对不确定性结果的影响，发现参数LZSN和AGWRC具有较大相关性，是参数不确定性的原因之一.

3)模型内存在大量“异参同效”现象，证明了GLUE的思想：对模拟结果影响的是参数组合而不是单一参数.

4)选取2006—2008年月径流研究妫水河流域不确定性，以纳什系数Ens为似然函数并以0.3为临界值，评估先验分布和后验分布的90%置信度的不确定性范围，结果在可接受范围.

文中纳什系数偏低(最高0.54)，分析认为该地区面临严重的水资源短缺问题，河流流量急剧下降，由径流过程线看出该区域的径流量很小，生产生活和农业灌溉等人为因素对该区径流量影响就会很大，实测径流量也就会因人为因素而产生较大差异；且本研究根据研究区降雨-径流散点图发现，径流与降雨相关性较小，也从另一方面说明此问题.此外，研究组使用相同的数据尝试通过其他水文模型，包括SWAT、MIKE SHE模型，研究该流域的不确定性，纳什系数均在0.5左右，对比分析HSPF模型较适合该流域研究，为HSPF模型在该流域其他研究提供依据并具有很好的指导意义.