2. 吉首大学生物资源与环境科学学院,吉首 416000
2. College of Biology and Environmental Sciences,Jishou University,Jishou 416000
近年来,灰霾现象在我国日趋严重.研究发现,较高的大气细颗粒物(PM2.5)浓度及相对湿度是造成严重灰霾污染的主要因素(Parrish et al., 2009).PM2.5的危害不仅表现在降低大气能见度方面,更重要的是它会严重威胁城市居民的身体健康(Nel,2005).目前,我国存在四大灰霾严重污染区域:京津冀地区、四川盆地、珠江三角洲和长江三角洲(吴兑,2011).有关灰霾期间高浓度PM2.5演化的数值模拟及预测预报,不仅在学术上具有重要意义,更是当前国家社会的迫切需要,具有重要的研究价值,并已成为当前大气环境研究领域的热点(费建芳等,2009;欧阳琰等,2007).
多年来,学者们基于大气物理、大气化学、气象学等方法提出了众多理论和模型,用以研究、模拟和预测大气颗粒物的时空演化.这些模型中尽可能详尽地包含了各种大气污染物之间的相互作用,以及污染物与气象因素之间的相互作用,如排放、对流、湍流、输运、冷凝、蒸发、凝聚、成核、沉降和多相化学反应等,其物理意义明确,并取得了卓有成效的进展(欧阳琰等,2007;Cobourn,2010;王自发等,2008;Chen et al., 2007).然而,这些模式所涉及的计算参数众多、方程繁杂、参数估计工作巨大.同时,由于大气环境的复杂性,模型中许多过程并不明晰,如大气化学中化学成分组成、反应速率、反应条件等存在较多不确定性因素,这给PM2.5的预测尤其是不利天气下高浓度污染的准确预测预报带来了很大的困难.因此,人们对PM2.5时间演化的动力过程并没有得到明确的认识.同时,尽管各模型所基于的理论和功能有较大差异,但基于确定性还原论思维的颗粒物污染模式实际上均暗含了这样一种基本假设:只要知道了所有影响因子及其相互作用机制,就可以对大气颗粒物的时空演化做出确定性的预测.但实际上,大气环境系统是典型的复杂巨系统,其组成单元数目庞大,单元之间存在强烈的反馈与调节的非线性相互作用.对于这样的复杂系统,要穷尽涉及PM2.5的所有影响因素及其作用机制显然是不可能的,也没有必要.从复杂性理论来看,PM2.5时间演化过程是开放、耗散的大气巨系统在人为污染作用下的复杂现象,其形成与演化既受到微观的物理化学等机制的影响,同时也表现为宏观、整体性系统动力学的结果.但目前对PM2.5浓度长时间演化的系统动力学总体特征,如“总体上,浓度差异很大的长期PM2.5波动是否存在着具有普适性的、确定的统计分布规律?究竟是什么宏观动力机制控制这些统计分布规律的形成?”等整体性的理论问题缺乏认识.
自组织临界(Self-Organized Criticality,简称SOC)理论是Per Bak等(Bak et al., 1987)为解释复杂系统的非线性宏观特征提出的新概念.这类系统包含着众多的发生短程相互作用的组元,在外界输入的能量和物质驱动下,能自发向一种宏观动力学稳定的临界状态演化,称之为自组织临界状态.在此临界状态下,一个小的扰动可能通过连锁反应而对系统中大量数目的组元发生影响,从而导致大规模事件的发生.虽然这类系统发生的小事件比大事件多,但由于长程相互作用的影响,遍及所有规模的连锁反应成为动态特征的一个必不可少的部分,因此,所有的时空关联函数都是幂律的,长期持续性、分形幂律等非线性结构特征在宏观上就涌现出来.真实沙堆系统是SOC的典型范例.在由Frette等(1995)进行的试验中,采用在圆盘上逐粒加沙的方式构造沙堆,当沙堆的倾角在临界角附近时,加入的沙粒数量与落在边缘之外的数量总体上达到平衡,沙堆停止增长. 此时对新添加沙粒的响应是临界态的,沙粒可能固定在沙堆上,也可能引起小范围沙粒的滑动,还可导致更大规模的崩塌,但宏观上来看,总是呈现崩塌规模与出现频率成反比的幂律关系.
许多复杂的自然现象,如地震、火灾发生、滑坡、大气降水、水华暴发、酸沉降等,均发现了幂律统计分布规律,目前已在SOC理论框架下得到满意的解释(Bak et al., 1989;Turcotte et al., 2004;Richard et al., 2008;Wang et al., 2011;Peters et al., 2006;刘信安等,2005;Zhu et al., 2003).具体领域中SOC机制的辨识,使得人们可以从宏观动力学的角度来对极端事件的发生进行准确的风险评估和预测.这些新颖的思想使得SOC理论可以为自然灾害的预测和减灾提供新的理论依据,相关研究也已成为复杂性科学前沿课题之一.
前期研究中,笔者发现空气污染长期演化过程中,污染浓度的出现频度遵循幂律分布统计规律,推测城市空气污染演化可能也具有一种内禀的SOC动力机制(Shi et al., 2008);进一步基于SOC理论,结合PM10、SO2、NO2这3种污染物的物化性质,建立大气污染数值沙堆模型,可以定量解释典型城市大气中这3种污染物演化中所出现的幂律统计分布规律(Shi et al., 2009).尽管相关工作还存在许多不足之处,如监测数据分辨率比较粗(利用的是污染浓度日均值)等,但这已表明,基于SOC理论,有助于加深空气污染复杂动力演化过程的认识.但相关研究并未涉及到特定灰霾时间段高浓度PM2.5污染演化动态,尚不清楚PM2.5污染演化是否具有SOC特征.因此,本文以成都一次典型重度灰霾发生期间为研究时段,研究大气PM2.5污染演化宏观动态的统计分布规律及其长期持续性;进一步基于SOC理论,建立特定时段大气PM2.5污染数值沙堆模型,论证大气PM2.5的自组织临界特性,以揭示灰霾期间PM2.5波动所具有的统计分布规律的产生机制.
2 研究数据(Data sets)2013年1—2月期间,四川省成都市陆续出现大范围、长时间、高浓度的严重霾污染.成都市区共设置8个国家网空气质量自动监测站点(即草堂寺、人民公园、梁家巷、金泉两河、十里店、沙河铺、三瓦窑、灵岩寺监测站点),监测数据发布于中国环境监测总站重点城市空气质量实时发布平台.本文选取成都市2013年1月25日—2月7日一次典型重度灰霾期间城区这8个监测站点连续的PM2.5小时平均浓度数据为研究数据.由于仪器校准、停电、设备故障等原因,该时间段内各监测站点PM2.5数据有零星缺失,但数据缺失率均不超过1%.对于所缺失的数据,采用缺失数据前后时刻监测浓度值加和平均的方法进行填补.8个监测站点数据列总长度均为336个.
此次灰霾期间,成都市平均气温为6.4 ℃,平均相对湿度为70.8%,背景风场为静风控制,平均风速仅为1.2 m · s-1,研究时段内降雨量为0.上述气象资料来源于成都市双流国际机场气象观测站(http://www.wunderground.com).
3 研究方法与模型(Methodology and model) 3.1 污染浓度波动的频度统计分析如果某一事件的发生规模在统计上表现出幂律分布,则具有标度不变特征,这被认为是可能出现SOC行为的一个显著标志.这通常描述为事件发生的频率随事件的规模大小而呈现幂指数下降(Shi et al., 2009;2013).对PM2.5浓度波动数据来说,如果具有相类似的特征,则应满足关系:
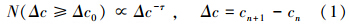
长期持续性的特征是时间序列的自相关函数以幂律形式缓慢衰减,以至相距较远的时间间隔仍具有显著相关性,系统过去的特征可以持续影响其当前和未来的状态(Shi et al., 2009).消除趋势波动分析方法(Detrended Fluctuation Analysis,简称DFA分析)(Peng et al., 1994)作为一种标度分析工具,可以有效滤去各阶趋势成分,能够很好地消除非平稳序列中的伪相关现象,科学地检测非平稳序列中的长期持续性.目前,该方法已经广泛应用于自然科学许多领域,且主要研究序列中DFA波动函数F(n)与时间尺度n之间是否存在如下关系:
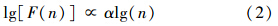
前期研究中,作者基于自组织临界理论构建了宏观空气污染过程的沙堆模型,可以定量模拟和解释SO2、NO2和PM10污染的长程相关性和标度不变特征(Shi et al., 2013).在此基础上,考虑到此次灰霾期间成都市的气象因素,作者进一步构建了大气PM2.5数值沙堆模型.该模型属于一类持续的、非守恒性的、衰减的、各向同性的元胞自动机模型,模型的构建思路如下.
首先将所研究的城市近地层大气映射到一个二维开放平面,用L×L的二维方格子表示.该二维方格子中某一个格点都具有一定的数值h(i,j),将其映射为城市某一空间位置(i,j)处近地层大气PM2.5浓度h(i,j).一次和二次PM2.5污染物持续输入到该二维方格子中.如果某一位置(i,j)的PM2.5浓度h(i,j)累积达到某一环境临界值hc时,该位置处的PM2.5污染物将处于临界不稳态,并向其四周迁移扩散.这个过程有可能会导致近邻空间中PM2.5污染物浓度也达到临界值,这样就可能导致某种链式作用,映射为PM2.5在迁移扩散过程中的浓度波动.迁移扩散的PM2.5污染物在空间输送过程中,由于物理沉降、碰并、凝结、化学反应等因素,迁移过程中将会带来一定的PM2.5污染物的损耗.同时,在大气自净作用下,大气中一次和二次PM2.5污染物将在各种物理、化学作用机制下进行衰减,因此,该模型在时空演化过程中物质是非守恒的.该模型的具体算法表述如下.
3.3.1 一次和二次PM2.5污染产生规则随机向L×L格子中任意一个格子投加“污染物”沙粒 Δh ,Δh包含了一次和二次PM2.5污染物,则:
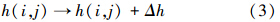
当某一位置(i,j)的PM2.5浓度h(i,j)达到某一环境临界值hc时,该位置处的污染物将处于临界不稳态,并向周围进行迁移扩散.考虑到当某局域空间(i,j)的PM2.5污染物迁移扩散后,该空间上仍将保留有部分的PM2.5污染物,保留量所占比例为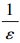 ,因此:
,因此:
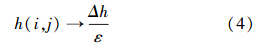
考虑到此次灰霾期间,成都市背景风场为静风控制,因此,认为处于局域不稳态的PM2.5表现为向其四周各向同性的迁移扩散,迁移扩散的PM2.5污染物按照公式(5)~(8)分配到其近邻空间.研究时段内降雨量为0,因而算法中不考虑降水的影响.PM2.5污染物在空间迁移扩散过程中,会由于物理沉降、碰并、凝结、化学反应等因素带来污染物的损耗,设定损耗所占比例为θ.
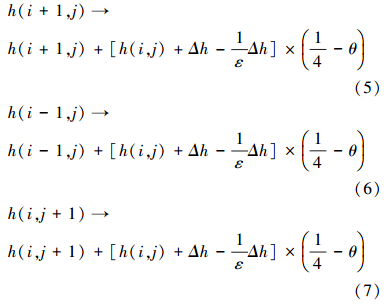
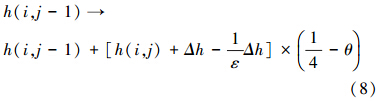
如果位置(i,j)的近邻由于公式(4)~(8)变得不稳定,那么它也将进一步按公式(4)~(8)迁移扩散.直到所有位置h(i,j)< hc.大气是开放的,因此,该迁移扩散规则允许污染物沙粒通过边界L×L离开该系统.
3.3.3 大气自净作用规则在大气的自净作用下,PM2.5污染物将在各种物理、化学作用机制下随时间衰减.假定按一阶指数衰减模式进行,即每次投加污染物后:
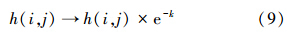
当所有格点都达到稳定态时,新投加一粒“污染物”沙粒,按照上述3个动力机制依次重复上述步骤,继续让系统的演化进行下去.系统的演化过程中会形成一系列的各种大小的崩塌.模型中主要研究的物理量——崩塌大小s定义为:每投放一次污染物,发生一次崩塌所影响的格子总数.如果PM2.5污染物的输送过程处于自组织临界态,s与其累积概率分布函数P(s)之间一般满足幂律统计关系,其幂指数为 σ ,即:

最后对模型中设定的参数做一说明.将每次投加的一次和二次PM2.5污染物归一化,即令 Δh=1 ;公式(4)中,假定某空间(i,j)的PM2.5污染物向其四周完全均匀地迁移扩散,则保留在原空间(i,j)处的PM2.5污染物将是原来的1/5,故令ε=5;空间迁移扩散过程中,假定由于物理沉降、碰并、凝结、化学反应等因素带来的PM2.5污染物的损耗量为1%,则θ=0.01;最后,根据自组织临界理论中经典的Bak-Tang-Wiesenfeld(BTW)沙堆模型(Bak et al., 1987;Turcotte et al., 2004),设定 Δh=1 和 hc=4.
4 研究结果与讨论(Results and discussion) 4.1 PM2.5污染浓度波动的频度统计分布图 1中的小图是以沙河铺这个监测站点为例,具体给出了PM2.5小时平均浓度波动的累积频度统计分布.在浓度波动值较大的区间,利用最小二乘法对分析数据进行线性回归,发现PM2.5小时平均浓度波动的频度分布关系为:
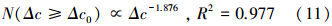
可见,此次成都灰霾期间沙河铺PM2.5小时平均浓度的波动与大于该波动值所出现的次数之间存在着良好的负幂律分布关系.同时也发现,污染浓度波动值较小的区域显著偏离幂律关系,出现这种情况的主要原因是:统计的小时平均浓度忽略了大量低于小时尺度内空气中表现出的较小污染浓度波动值,大多数小污染浓度波动点的丢失导致了在双对数坐标下线性关系的偏离,这种现象降水过程中也发现过(Peters et al., 2006).
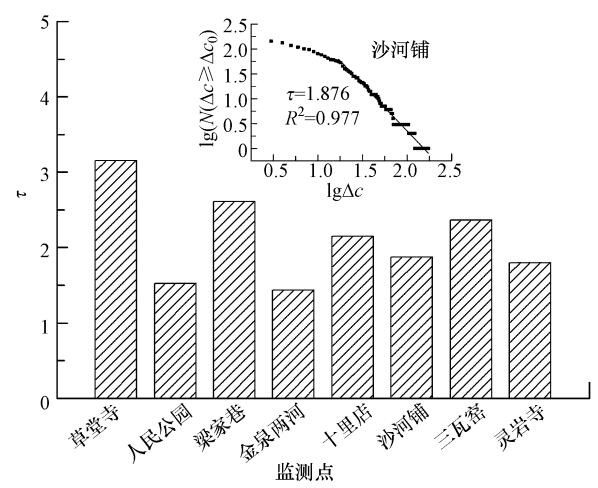 |
| 图 1 成都市区各监测点PM2.5频度统计分布的标度指数 Fig. 1 Frequency analysis results of PM2.5 pollution at eight air monitoring stations of Chengdu |
各监测站点PM2.5的标度指数(τ)结果如图 1的柱状图所示,计算结果分别为:草堂寺(τ=3.154)、人民公园(τ=1.525)、梁家巷(τ=2.610)、金泉两河(τ=1.436)、十里店(τ=2.149)、沙河铺(τ=1.876)、三瓦窑(τ=2.367)、灵岩寺(τ=1.798).尽管各监测站点数据之间存在差异,但总体上来看,各站点PM2.5小时平均浓度波动的累积频度分布均服从负幂律分布.各监测站点的PM2.5标度指数差异较大,反映出此次灰霾期间,成都市PM2.5时间统计规律在空间分布上具有一定差异性.进一步采用针对小样本数据的Lilliefors检验方法对各监测站点PM2.5标度指数的统计特征进行分析,检验结果表明,PM2.5标度指数在95%置信区间上符合正态分布.因此,尽管各监测点数据幂律分布特征之间存在差异,但从统计学上可以认为其幂律标度指数均来自正态样本空间.
4.2 PM2.5污染的DFA分析结果图 2中的小图是以沙河铺监测站点为例,运用DFA方法对其PM2.5浓度时间序列进行分析.在整个研究时间尺度内,lgF(n)与logn呈现较好的线性关系,α=0.945表明沙河铺监测点的PM2.5浓度序列具有明显的Hurst效应,即在该灰霾期间PM2.5浓度波动具有很强的长期持续性特征.该特征表现为:在一定时间尺度范围内,PM2.5浓度序列的相关性随时间的变化并不遵循经典的马尔科夫过程(Markov Process),即相关性不随时间呈现指数衰减,而遵循缓慢的幂律衰减规律.这也意味着在过去某一段时间内PM2.5浓度会持续影响未来一定时间尺度内PM2.5浓度的变化趋势.
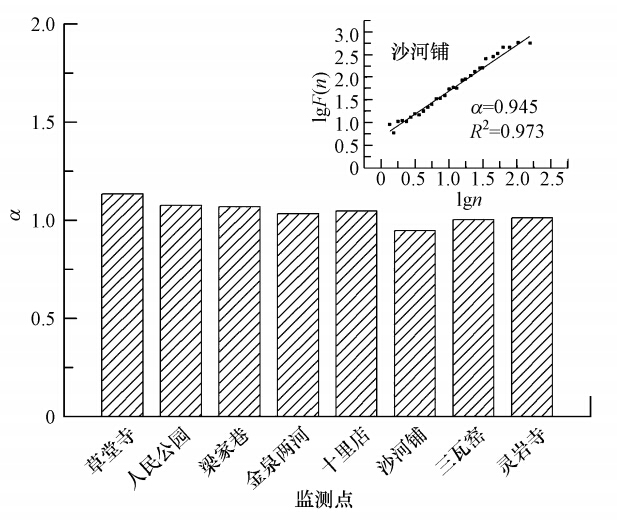 |
| 图 2 成都市区各监测点PM2.5浓度时间演化的DFA指数 Fig. 2 Detrended fluctuation analysis results of PM2.5 pollution at eight air monitoring stations of Chengdu |
各监测站点PM2.5的DFA指数(α)结果如图 2的柱状图所示,计算结果分别为:草堂寺(α=1.133)、人民公园(α=1.074)、梁家巷(α=1.068)、金泉两河(α=1.032)、十里店(α=1.046)、沙河铺(α=0.945)、三瓦窑(α=1.112)、灵岩寺(α=1.011).各监测点PM2.5的DFA指数均显著高于0.5,展现出很强的长期持续性特征.进一步采用针对小样本数据的Lilliefors检验方法对各监测站点PM2.5的DFA指数的统计特征进行分析,检验结果表明,PM2.5的DFA指数在95%置信区间上符合正态分布,从统计学上可以认为不同空间位置上PM2.5波动的DFA指数均来自正态样本空间.
4.3 大气PM2.5数值沙堆模型模拟结果首先选取了网格规模为50×50的二维网格,网格点初始赋值为0,用格子内的平均颗粒数μ来反映系统是否进入临界稳定态.定义平均颗粒数为:
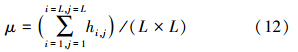
为了保证计算有严格的统计意义,且真实反映数值沙堆系统的演变趋势,最初的106次崩塌被忽略,统计随后的107次崩塌的统计分布,主要目的是使系统进入非平衡稳定态.
图 3展现了当PM2.5污染物的宏观时间衰减系数k=1.704×10-4、崩塌次数为5万次时格子内μ的变化趋势.结果表明,μ能很好地表现出系统是如何进入自组织临界态的,它可作为表征临界点的性态参数.μ随投放过程而逐渐演化,投放约1万次左右沙堆就达到其吸引子(即临界值2.124),并在此吸引子附近非线性涨落,此时系统进入临界态,对外界扰动具有鲁棒性.
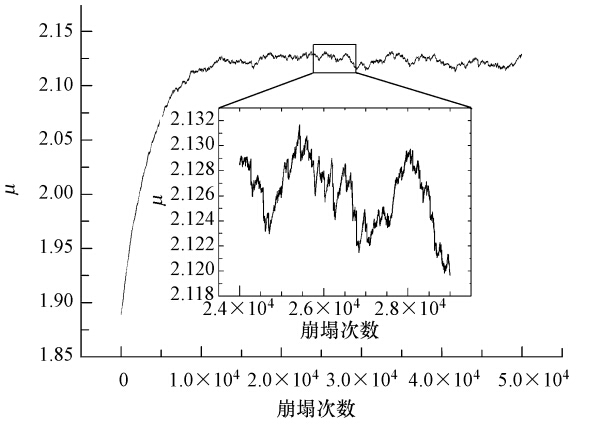 |
| 图 3 k=1.704×10-4时格子内μ的变化趋势 Fig. 3 Plot of average height μ against the number of avalanches when k=1.704×10-4 |
当k=1.704×10-4时,系统崩塌大小 s 统计分布的模拟结果如图 4所示.模拟结果表明,崩塌大小s与其统计频度P存在显著的幂律关系,能用 P∝s-σ 进行描述.标度指数σ可以用最小二乘法进行拟合,结果为1.877.图 4中的数值模拟结果与图 1中实际观察到的沙河铺PM2.5频度统计分布规律(即公式(10))完全一致.
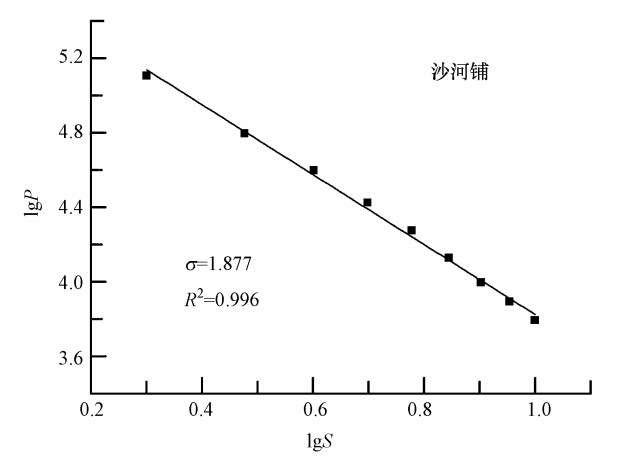 |
| 图 4 k=1.704×10-4时大气PM2.5数值沙堆模型模拟计算获得的崩塌大小统计分布 Fig. 4 Avalanche size distribution for the PM2.5 pollution s and model when k=1.704×10-4 |
进一步模拟发现,PM2.5宏观时间衰减系数k决定了崩塌大小统计分布规律的标度指数σ.图 5确定了k与σ的定量关系,发现二者呈现指数关系,即σ=-0.459+0.209e14213.0k.这样,尽管各监测点PM2.5频度统计分布特征之间存在差异,但公式(1)中频度统计分布的标度指数(τ)均可根据该模型进行定量模拟,定量模拟得到的标度指数(σ)结果如图 5所示.需要强调的是,模型中k值是PM2.5宏观时间衰减系数,其数值大小仅仅与PM2.5污染物在大气环境中的自净能力有关,属于PM2.5污染演化系统的内在参量,不同空间位置的k值有所差异.由图 5可见,设定不同的k值,基于SOC理论建立的大气PM2.5数值沙堆模型能很好地模拟出成都市各监测站点观测到的PM2.5演化宏观统计分布规律.
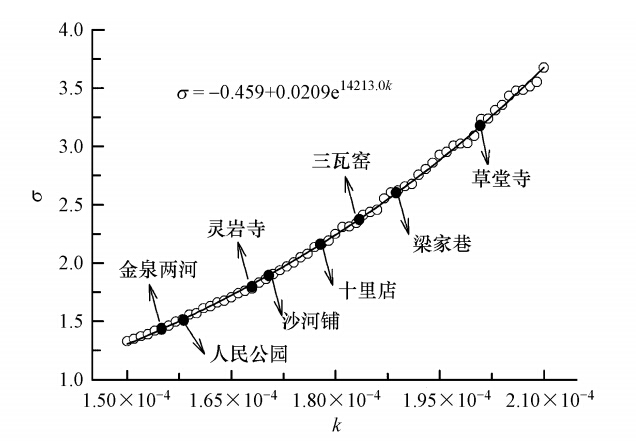 |
| 图 5 各监测点PM2.5频度统计分布的标度指数的模拟值及k与σ的定量关系 Fig. 5 k values dependence of avalanche size distribution parameters(σ)in the PM2.5 pollution s and model |
2013年1—2月,包括成都市在内的我国大部分地区持续遭遇重度霾天气,多地PM2.5值时常濒临“爆表”,空气污染极其严重.四川盆地由于受到独特的地理位置和气象条件的影响,灰霾天气的发生有其特殊性,主要表现为:盆地内近地层区域静风频率较高,大气输送条件较弱,大气污染物不易扩散;大气颗粒物主要来源于局地污染源;灰霾天气往往形成于气流停滞区域.以成都市为例,其多年平均静风频率高达42%,边界层大气结构相对稳定,大气中PM2.5浓度长期居高不下,全年霾日天数超过150 d,列全国第6.这些因素构成了此次成都市严重空气污染的背景条件.
然而,本文进一步发现,此次灰霾期间成都市各站点PM2.5小时平均浓度波动的累积频度分布均服从负幂律分布.这一普适性的统计分布规律如何定量解释?我们构想PM2.5可能存在这样的内在动力演化过程:大气中的PM2.5既包含一次污染物,也可由二次污染产生.在不利天气条件(不利于大气扩散的天气形势和强稳定层结,多伴随静风出现)下,PM2.5演化动力受内禀SOC机制主导控制.大气系统这一开放巨系统,其中包含的众多发生短程相互作用的组元,会自发向着某个临界状态演化.一旦达到临界状态,将通过与外界能量和物质的交换,使PM2.5的演化趋势将在一定时段内锁定在这个临界动力状态下.在该临界状态,大气系统中的一个微小扰动都有可能在大气系统中诸多组元间引起连锁反应,产生极大的影响,从而导致较高的PM2.5浓度波动的产生.宏观上来看,PM2.5浓度波动统计上服从负幂律分布.
真实沙堆系统是SOC的典型范例.为了进一步解释PM2.5演化内禀SOC机制,可将PM2.5演化与沙堆作类比.此次灰霾期间,成都市各种污染源持续向城市大气环境中排放大气污染物,这个过程类似于向一个平板某一边界上持续投入沙粒,这是大气污染系统演化的直接驱动力.局域空间中大气环境容量类比于沙堆的临界倾斜角.当PM2.5物质在局域大气中聚集超过一定浓度时,可能由于碰并、凝结等过程形成更大粒径的粒子,当空气动力学直径最终大于2.5 μm,此时颗粒物就不再属于PM2.5的范畴;粒径更大时,可能通过沉降方式离开大气系统,这将造成PM2.5浓度减小.这正如沙堆达到临界倾斜角之后,将以“塌方”方式将多余的沙粒排除掉,以维持其倾斜角的稳定性.沙堆崩塌过程演化到临界状态时,沙粒之间相互挤压的短程相互作用将演化为长期持续性作用,即每一次“塌方”的大小与其以前很长时间内的“塌方”大小有关系.处于临界状态的PM2.5浓度波动,其演化也具有长期持续性特征,这将导致在一定时间尺度范围内,PM2.5浓度序列的相关性随时间的变化遵循缓慢的幂律衰减规律,从而在过去某一段时间内PM2.5浓度将会持续影响未来一定时间尺度内PM2.5浓度的变化趋势.宏观来看,持续投加的沙粒并不产生连续稳定的沙堆崩塌,而是产生幂律分布的崩塌事件.与之类似,大气系统中持续累积的PM2.5物质并不产生持续稳定的PM2.5浓度波动,相反却产生大小按照幂律分布的非线性浓度波动事件.这样,此次成都灰霾期间PM2.5浓度波动时间演化过程与沙堆崩塌事件具有相似性.
从复杂性理论来看,此次成都灰霾期间,大气环境处于不利于大气扩散的天气形势和强稳定层结的大气系统背景下,而PM2.5浓度的波动演化则表征为多因素局部相互作用、相互影响所导致的宏观效应.一方面,大气PM2.5的浓度波动表现为区域特定的污染排放(包括污染排放方式、污染排放量、大气污染物种类等)和自然环境特征(包括气象要素、地形地貌、太阳辐射、下垫面特征等)的综合影响,在一定程度上具有确定性.另一方面,由于大气系统是一个开放的耗散系统,影响PM2.5演化的各种因素及其相互作用非常复杂,且不是确定性的,因而PM2.5演化在时空上表现为不规则、非线性变化,具有复杂系统的基本特征.宏观上综合来看,各种因素之间相互作用,并共同对PM2.5的浓度波动产生影响,即形成具有确定性统计特征的“有序”结构,即本文中由标度指数τ和DFA指数α所表征的PM2.5演化的宏观特征.因此,从复杂性的观点来看,此次成都灰霾期间,大气PM2.5的浓度波动实质上是其SOC内禀机制导致的.PM2.5浓度波动的幂律统计分布和长期持续性特征则是SOC行为的标志.而成都市各个监测站点PM2.5浓度波动标度指数的变化,则反映了自组织过程中具体空间位置环境特征对PM2.5的影响.此次成都灰霾期间PM2.5浓度波动SOC机制的辨识,说明灰霾的产生及演化中所出现的大的PM2.5浓度波动事件的产生动力机制从本质上说和小的PM2.5浓度波动是一样的.
根据SOC理论,SOC内禀机制起主要作用的系统属于弱混沌系统,其初始条件的微小差异随时间按幂律规律增长,而不是呈指数发散,系统在混沌边缘上的演化不存在时间标度,因而可以对该系统进行预测预报,其可预测性甚至比经典的混沌系统还要好.这样,在系统辨识SOC特征的基础上,利用SOC物理普适性原则确定的极端事件发生的幂律分布关系和时间演化关联函数,可以建立极端事件发生的风险预测模型.相关风险预测方法已经在电网停电事故(于群等,2007)、火灾发生(王静虹等,2010)、斜坡灾害(何越磊等,2005)等实际领域中取得了进展.对于PM2.5来说,尽管从理论上讲,整个大气环境系统中与PM2.5形成及演化的所有细节是可测量的,但实际上需要测量的细节如此之多以至于根本不可能完成准确测量,这也导致许多PM2.5形成及演化的参数存在较多的不确定性,影响了现有PM2.5数值模型的预测效果.而根据本研究,在系统辨识PM2.5自组织演化临界状态的基础上,应用统计方法进一步通过过去时段内各种PM2.5浓度的发生频率来计算推测未来高浓度PM2.5的发生概率和风险,有助于从新的角度来建立或改进不利天气下高浓度PM2.5污染预测预报模型.PM2.5浓度时空波动幂律规律及其SOC动力机制的阐明,将使得人们可以从宏观动力学的角度来对高浓度PM2.5的发生进行准确的风险评估,这对于PM2.5的预测尤其是不利天气下高浓度污染的风险评估有着重要意义.
5 结论(Conclusions)应用频度统计分析和消除趋势波动分析方法,发现2013年1月25日—2月7日成都市一次典型重度灰霾期间,8个城区监测站点的PM2.5小时平均浓度波动的累积频度分布均服从负幂律分布,其幂律标度指数分别为草堂寺(τ=3.154)、人民公园(τ=1.525)、梁家巷(τ=2.610)、金泉两河(τ=1.436)、十里店(τ=2.149)、沙河铺(τ=1.876)、三瓦窑(τ=2.367)、灵岩寺(τ=1.798).同时,PM2.5的时间演化在时间尺度上表现出很强的长期持续性特征,这也意味着在过去某一段时间内PM2.5浓度会持续影响未来一定时间尺度内PM2.5浓度的变化趋势.考虑到此次灰霾期间成都市的气象因素,基于自组织临界理论进一步构建了大气PM2.5数值沙堆模型.该模型略去了众多微观物理化学机制,直接从宏观整体性的角度入手,包含了一次和二次PM2.5污染产生规则、灰霾天气条件下PM2.5迁移扩散规则、大气自净作用规则等主要机制,属于一类持续的、非守恒性的、衰减的、各向同性的元胞自动机模型.数值模拟表明,大气PM2.5数值沙堆模型表现出稳健的自组织临界行为,模拟的各站点PM2.5小时平均浓度波动的累积频度分布也均服从负幂律分布,其幂律标度指数分别为草堂寺(τ=3.155)、人民公园(τ=1.524)、梁家巷(τ=2.610)、金泉两河(τ=1.436)、十里店(τ=2.150)、沙河铺(τ=1.877)、三瓦窑(τ=2.366)、灵岩寺(τ=1.798).模拟结果能很好地阐明此次灰霾期间大气PM2.5浓度时空波动的幂律统计分布和长期持续性特征的产生机制.模拟结果和实际结果的高度一致,表明该模型真正阐明了导致PM2.5浓度时空波动的重要动力机制.成都市灰霾期间,大气PM2.5的时空演化已达到某种临界状态,并在一定时段内通过与外界能量和物质的交换锁定在此临界动力状态下,PM2.5的浓度时空波动实质上是其SOC内禀机制导致的.灰霾期间PM2.5宏观演化所涌现出的复杂特征,如PM2.5浓度波动的幂律统计分布和长期持续性特征,则是SOC动力机制的表观标志.PM2.5自组织临界性的辨识为理解灰霾的形成、发展及演化提供了一种新的研究思路,有助于从宏观动力学的角度对高浓度PM2.5的发生进行准确的风险评估和预测.
| [1] | Bak P,Tang C,Wiesenfeld K.1987.Self-organized criticality:an explanation of the 1/f noise[J].Physics Review Letters,59(4):381-384 |
| [2] | Bak P, Tang C.1989.Earthquakes as a self-organized critical phenomenon [J].Journal of Geophysical Research,94(B11):15635-15637 |
| [3] | Cobourn W G.2010. An enhanced PM2.5 air quality forecast model based on nonlinear regression and back-trajectory concentrations[J].Atmospheric Envi-ronment,44(25):3015-3023 |
| [4] | Chen D S,Cheng S Y,Li J B,et al.2007.Application of LIDAR technique and MM5-CMAQ modeling approach for the assessment of winter PM10 air pollution:a case study in Beijing,China[J].Water,Air and Soil Pollution,181(1/4):409-427 |
| [5] | 费建芳,王锐,王益柏,等.2009.一次大雾天气下PM2.5二次无机粒子的数值模拟[J].大气科学学报,32(3):360-366 |
| [6] | Frette V,Christensen K,Malthe A,et al.1995.Avalanche dynamics in a pile of rice [J].Nature,379(6560):49-52 |
| [7] | 何越磊,姚令侃,苏凤环,等.2005.斜坡灾害自组织临界性与极值分析[J].中国铁道科学,26(2):15-19 |
| [8] | 刘信安,马艳娥,陈双扣,等.2005.用准真实沙堆模型的自组织临界特性研究流域水华暴发行为[J].自然科学进展,15 (12):1441-1446 |
| [9] | Nel A.2005.Air pollution-related illness:Effects of particles[J].Science,308(5723):804-806 |
| [10] | 欧阳琰,蒋维楣,刘红年.2007.城市空气质量数值预报系统对PM2.5的数值模拟研究[J].环境科学学报,27(5):838-845 |
| [11] | Parrish D D,Zhu T.2009.Clean air for megacities [J].Science,326(5953):674-675 |
| [12] | Peng C K,Buldyrev S V,Havlin S,et al.1994.Mosaic organization of DNA nucleotides[J].Physical Revi-ew E,49(2):1685-1689 |
| [13] | Peters O,Neelin J D.2006.Critical phenomena in atmospheric precipitation[J].Nature Physics,2(6):393-396 |
| [14] | Richard H G,Peter J D,Raymond A C,et al.2008.Exploring the magnitude-frequency distribution:a cellular automata model for landslides[J]. Landslides,5(1):151-159 |
| [15] | Shi K,Liu C Q.2009.Self-organized criticality of air pollution[J].Atmospheric Environment,43(21):3301-3304 |
| [16] | Shi K,Liu C Q,Ai N S,et al.2008.Using three methods to investigate time scaling properties in air pollution indexes time series[J]. Nonlinear Analysis:Real World Applications,9(2):693-707 |
| [17] | Shi K,Liu C Q,Li S C.2013.Self-organized criticality:emergent complex behavior in PM10 pollution[J].International Journal of Atmospheric Sciences,doi:10.1155/2013/419694 |
| [18] | Turcotte D L,Malamud B D.2004.Landsli-des,forest fires,and earthquakes:examples of self-organized critical behavior[J].Physica A,340(4):580-589 |
| [19] | 吴兑.2011.灰霾天气的形成与演化[J].环境科学与技术,34(3):157-161 |
| [20] | 王静虹,谢曙,孙金华.2010.城市火灾自组织临界性判断及大火灾损失极值分析[J].科学通报,55(22):2241-2246 |
| [21] | 王自发,庞成明,朱江,等.2008.大气环境数值模拟研究新进展[J].大气环境,32(4):987-995 |
| [22] | Wang J H,Xie S,Sun J H.2011.Self-organized criticality judgment and extreme statistics analysis of major urban fires[J].Chinese Science Bulletin,56(6):567-572 |
| [23] | 于群,郭剑波.2007.电网停电事故的自组织临界性及其极值分析[J].电力系统自动化,31(3):1-3;90 |
| [24] | Zhu J L,Liu Z G.2003.Long-range persistence of acid deposition[J].Atmospheric Environment,37(19):2605-2613 |
 2014, Vol. 34
2014, Vol. 34


