随着现代工业进程的快速发展，湖库水体富营养化现象日趋严重，由此而导致的藻类水华暴发给水环境的生态结构及经济社会带来了严重的影响(Cui et al., 2009).因此，对湖库藻类水华形成机理深入分析，进而对藻类水华暴发这一突发情况进行有效识别，可为相关部门采取及时有效的水华防治措施提供可靠的依据.

近年来，湖库水体富营养化机理研究在理论和实践方面都有较大的发展，研究人员已建立了大量复杂程度不同的水体富营养化机理模型(Pettersson et al., 2001).贾海峰等(2009)在参考水质WASP模型和生态CAEDYM模型的基础上，构建了藻类生态动力学模型，描述了浮游植物、氮、磷和溶解氧4个子系统的动力学关系，较好地模拟了城市水系的藻类生长状况.Chau(2005)通过不同的研究周期，基于多次输入的水动力学参数与水质参数，将PSO优化用于训练感知器模型，并实时预测了Tolo海港的赤潮现象.董硕琦等(2012)提出用Agent智能仿真技术来构建湖库藻类水华形成的机理模型，对湖库藻类生消机理进行深入研究，并对藻类生长趋势和湖库水系的能量流动和物质流动状态进行了有效分析.刘载文等(2008)从Δt时段内叶绿素的质量平衡关系入手，构建了藻类生长模型，并通过有约束非线性极小值问题的求解方法获得模型的最优参数估计值，模型很好地反映了水华暴发前的藻类生长情况，而在水华暴发阶段和衰亡阶段出现了较大偏差.王小艺等(2012a)通过设计正交试验，结合粗糙集理论确定模型输入的关键因子，构建了城市湖库蓝藻水华形成的数学机理模型，并运用改进的粒子群算法对模型参数进行非线性优化率定，发现该模型较好地模拟了蓝藻的生长变化趋势，提高了模型的适用性及有效性.

由于湖库水体是一个开放性的复杂系统，现有的藻类水华形成机理建模方法无法准确、量化地描述水华暴发期间水体营养盐之间、营养盐与外环境等之间的关系(Lee et al., 2003).复杂网络是将复杂系统中相互作用的实体抽象成节点，通过节点间的相互作用反映出复杂系统中各实体的相互作用.因此，复杂网络能把现实中的模型描述成可见的模型，并可通过数学运算得到可见的结果，从而更加系统地描述藻类水华形成过程.基于此，本文在确定影响城市湖库藻类水华形成的主要影响因子基础上，建立水华形成识别的有向复杂网络模型，通过复杂网络统计特性分析，构筑水华暴发统计特征函数G，并进行半定量的分级，进而判断藻类水华的污染程度.

将复杂的湖库水体系统抽象成一个复杂网络，将影响藻类水华形成的主要影响因素抽象成网络节点，构成网络点集 V(V ={v₁，v₂，...，v_n})，节点数为n；将各主要影响因素间的关系抽象成网络的边，构成边集 E(E ={e₁，e₂，...，e_m})，边数为m，并且 E中所有的边都有V 中两个节点与之相对应.这种由 V和E 组成的网络拓扑图G=(V，E)表示湖库水体藻类水华形成特性.根据城市湖库水华形成机理特征，将总磷(TP)、总氮(TN)、温度(T)、pH 值、溶解氧(DO)、光照(I)、藻密度(chl_a)等7个关键影响因素构成点集 V，影响因素之间的相互关系构成边集 E，其中节点数n=7，边数m=14.构建的复杂网络的藻类水华形成有向网络模型如图 1所示.

图 1(Fig. 1)

图 1 湖库藻类水华形成识别的复杂网络结构 Fig. 1 The complex network structure for the recognition the lake algal bloom formation

复杂系统的数据特征往往通过其对应的复杂网络模型的统计特征表现出来，因此，复杂网络的统计特性成为很多学者的关注点(Newman，2003)，在此重点研究平均路径长度、聚类系数、节点介数和度分布等统计特性.其中，平均路径长度是对整个复杂网络是否会发生的相互之间关系的概率统计，聚类系数用来描述网络的耦合程度，节点介数的大小与节点在网络中的影响和作用相对应，节点的度能够反映节点的重要程度.

相关性分析是对各藻类水华形成影响因子之间的相关密切程度进行分析，以便获得各个影响因素与藻类水华形成的作用关系.为得出各影响因子之间的相关程度，对实际湖库水体数据进行实验分析，得出影响因子间的相关系数.其中，温度与叶绿素a的相关系数是0.867，说明与光照等影响因子相比，水体中叶绿素a含量受温度的影响较大；溶解氧和pH值与藻密度的相关系数也较大，说明溶解氧和pH值对水体中叶绿素a含量的影响较大；同时N、P和光照对叶绿素a的含量也有一定影响，但光照对叶绿素的直接影响相对较弱，这与实际情况完全符合.

定义各影响因子之间的相关系数为r_ij，各节点之间边与边的距离为D_ij(i，j=1，2.....7，n=7)，采用Floyd算法计算有向复杂网络边的最短距离(Tsai et al., 2004)，即：

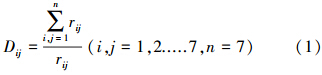
模型采用的数据为2007年阳光房模拟自然条件下的水华暴发监测数据，水样采自北京市玉渊潭公园，它是北京市二环水系的重要组成部分，具有很好的代表性.有向复杂网络边的最短距离及节点间最短距离计算结果见表 1、2>所示.

表 1(Table 1)

表 1 水华暴发识别有向复杂网络边的最短距离 Table 1 The shortest distance of the sides in the complex network for algal bloom recognition

表 1 水华暴发识别有向复杂网络边的最短距离 Table 1 The shortest distance of the sides in the complex network for algal bloom recognition T TP pH DO I TN chl_a 注：文中网络是有向的，因此，T→TP与TP→T的距离不同，表中的距离是列节点到行节点的距离，即T→TP的距离是6.6060；虽然计算出的各因子的相关性矩阵是对称矩阵，但在计算最短距离时，分别以每一行的和作为分子，这样在分母相同的情况下由于分子不同，所产生的结果也就不同. T 0 14.1027 5.8104 5.6862 26.1288 9.5708 4.9123 TP 6.6060 0 5.3774 ∞ ∞ ∞ 6.1957 pH 6.2196 12.2884 0 5.0154 ∞ 5.8374 5.9595 DO 4.4940 ∞ 3.7030 0 ∞ ∞ 4.7542 I 8.1963 ∞ ∞ ∞ 0 ∞ 7.7225 TN 6.3326 ∞ 3.6082 ∞ ∞ 0 4.7601 chl_a 5.1061 13.7485 5.7869 6.2528 25.5896 7.4780 0

表 2(Table 2)

表 2 水华暴发识别有向复杂网络节点间的最短路径 Table 2 The shortest distance of the nodes in complex network for algal bloom recognition

表 2 水华暴发识别有向复杂网络节点间的最短路径 Table 2 The shortest distance of the nodes in complex network for algal bloom recognition T TP pH DO I TN chl_a 注：根据网络拓扑结构，T可以通过节点2(TP)到达TP，而TP无法到达T.表中的最短路径表示列节点到达行节点的最短路径，“-”表示路径不存在，数字表示到达目的节点的前一个节点编号.例如，网络拓扑中I到TP的路径为I→T→TP，节点编号为1(T)，路径中只含有起始节点和目的节点的路径，则用目的节点的编号表示路径. T 1 2 3 4 - 6 7 TP - 2 3 - - - 7 pH - - 3 - - - 7 DO - - 3 4 - - 7 I 1 1 1 1 5 1 7 TN - - 3 - - 6 7 chl_a - - - - - - 7

计算结果表明，网络中的T到pH、chl_a、DO，以及TN、DO到pH等节点上计算的边距离比其余影响因子之间的边距离小，表示此复杂网络中比较容易通过上述的转移方式来达到最短距离，即T与pH、chl_a、DO，以及pH与TN、DO等这些元素之间的相互作用容易使水体发生富营养化变化.复杂网络边的距离中“∞”和“0”代表复杂网络中不存在这两个节点的相互作用，即相互之间的边也不存在.

湖库水体在一定条件下，T、TP、pH、DO、I、TN均不需要通过其他因子而直接到达节点7(叶绿素a)，即直接影响藻类水华形成.由表 2的结果得出节点之间的最短路径，根据节点v_i到节点v_j的平均路径长度L的公式(2)计算各节点的平均路径长度.

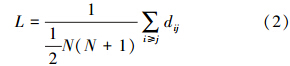
式中，d_ij为网络中节点v_i到v_j的距离，等于节点v_i和v_j之间相互连接的最短路径上的边数，节点到自身的距离为0，N为网络的节点数.

聚类系数C_i为任一节点v_i与其他相连节点之间实际存在的边数E_i与K_i个节点之间最多可能有K_i(K_i-1)/2条边的比值，可表示为：

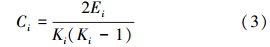
式中， K_i是节点v_i与其它节点连接的边数.整个网络的聚类系数C就是所有节点v_i的聚类系数C_i的平均值.很显然，聚类系数C的范围为0≤C≤10.

为更好地体现每个节点在复杂网络中的作用，构建节点的关键度模型为：

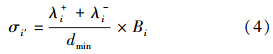
式中，d_min即节点v_i到叶绿素a计算的最短距离；λ⁺_i和λ^－_i分别表示相应节点v_i的入度和出度，节点度即节点的出度和入度的和，节点度越大就意味着该节点在整个网络中的作用越重要；B_i表示节点v_i的节点介数，反应整个网络中相应节点的影响和作用(Lin，1995)，节点介数越大，表明该节点在计算最短距离时被经过的次数越多，受各影响因子的综合协同作用越大，反应其在水华暴发中的作用越大.

考虑到平均路径长度和聚类系数对网络的影响，对节点的关键度模型进行二次修正，修正模型为：

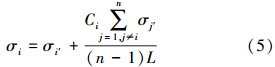
式中，C_i为节点的聚类系数，表示节点v_i与网络中其他节点的耦合程度，L为网络的平均路径长度.结合实际数据对复杂网络中各个参数进行分析，计算结果见表 3.

表 3(Table 3)

表 3 水华形成识别复杂网络的各参数值 Table 3 Various parameters of complex network for algal bloom recognition

表 3 水华形成识别复杂网络的各参数值 Table 3 Various parameters of complex network for algal bloom recognition 影响因子 节点度 最短距离 dmin 介数 Bi 关键度 σi 聚类系数 Ci 修正后关键度 σi 入度λ－i 出度λ+i 和λi 注：L=4.1218，C=0.2667. T 5 1 6 4.9123 2 2.4428 0.4000 2.5971 TP 2 1 3 6.1957 2 0.9684 0.2000 1.0598 pH 1 4 5 5.9595 5 4.1950 0.3333 4.2951 DO 2 1 3 4.7542 2 1.2620 0.2000 1.3506 I 2 0 2 7.7225 1 0.2590 0.1333 0.3245 TN 2 1 3 4.7601 2 1.2605 0.2000 1.3491

根据表 3可以看出，各影响因子对藻类水华形成的作用程度不尽相同.考虑C_i、B_i和σ_i等是水华形成复杂网络特性的关键参数，构建藻类水华形成的统计特征参数模型G：

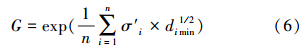
式中，G是水华形成的统计特征值；σ′_i为节点v_i的关键度σ_i与节点v_i的具体参数值的乘积，即σ′_i=c_i×σ_i，c_i表示节点v_i的具体参数值，n为节点数，n=6.

为验证藻类水华形成的统计特征参数G值的有效性，选取2组北京城市湖库水质监测数据进行计算，8月份数据用于对模型有效性进行验证，6月份数据用于对模型稳定性进行验证，结果如图 2所示.

图 2(Fig. 2)

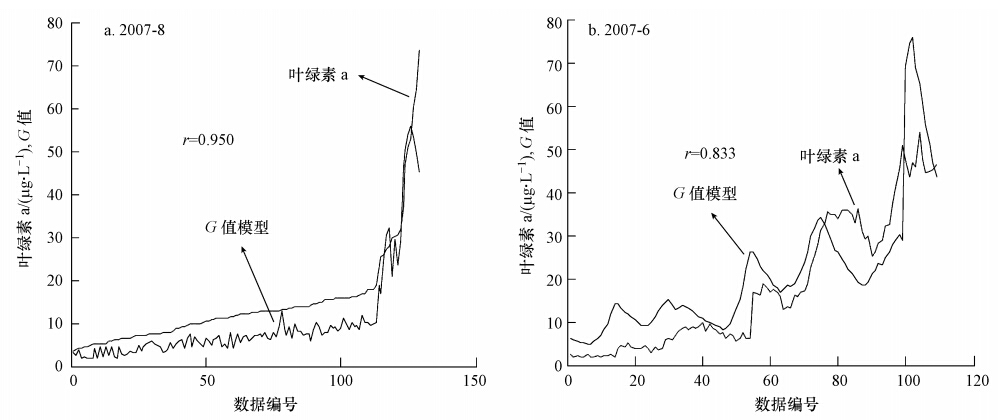图 2 复杂网络统计特征参数G与叶绿素a的对比 Fig. 2 Comparison between the statistical characteristic parameters G and chl_a

由图 2可知，藻类水华形成的统计特征参数G与表征水华形成的叶绿素a具有显著相关性.表明统计特征计算能够很好地反映藻类水华形成过程，同时相比叶绿素a还提供了更丰富的信息，在藻类生长的适应时期，G值变化比较平缓.在藻类生长的萌芽阶段，水体内部发生着显著的变化，能量流动呈现不稳定态势，G值在此萌芽阶段也同样出现震荡的不稳定现象.在水华暴发阶段，叶绿素a的数量发生突变，呈指数增长，此时G值也发生突变，以同样的方式增长.同时，由图 2b可知，G值的变化超前于叶绿素的变化，分析可知，所构建的水华形成复杂网络的统计特征参数G的数值模型能够较好地反应水华形成情况，能够较快地识别水华现象和水华暴发趋势.此外，对第2组数据的验证结果显示，该模型具有较好的稳定性.根据北京城市湖库水体特点及大量实验数据分析得出，叶绿素浓度超过40 μg · L^-1可认为水华暴发(王小艺等，2012b).根据G值与叶绿素的对应关系及实验结果可得出表 4所示的结论.

表 4(Table 4)

表 4 水华形成识别复杂网络的统计特征参数G与结果验证 Table 4 Statistical characteristic parameters G and the result about identification of algal-blooms outbreak

表 4 水华形成识别复杂网络的统计特征参数G与结果验证 Table 4 Statistical characteristic parameters G and the result about identification of algal-blooms outbreak G值 藻类生 长阶段 叶绿素a 浓度/ (μg·L-1) 水华暴发识别情况 ≤12 适应阶段 <20 水华暴发的可能性很小 15~45 萌芽阶段 20~40 出现水华暴发的趋势 ≥50 暴发阶段 >40 极易暴发水华或已经暴发

因此，复杂网络的统计特征参数G的数值模型能够直观地反映水体中叶绿素a的变化情况.当水体中影响水华暴发的关键因子的含量发生变化或有变化趋势时，由于叶绿素a的变化存在一定的滞后性，不能够快速地反映水华暴发的情况，然而通过对参数G的计算，能够快速识别水体中叶绿素a的变化情况和变化趋势，从而为有关部门及时采取预防和治理措施提供可靠的保障.

通过对水华形成的复杂网络识别模型进行验证，结果表明，复杂网络的统计特征参数G与叶绿素a浓度有显著的相关性.在藻类生长的适应期，G值变化平缓，在萌芽阶段，G值出现波动和振荡，在水华暴发阶段，G值发生突变呈指数增长，较好地表征了水华形成过程.同时，G值变化的超前性说明G值可以更快地对水华现象进行识别，萌芽阶段G值的波动性也充分显示该参数能够对系统的微小变化做出灵敏反应.两组不同数据的模型验证结果显示，该模型具有较好的稳定性.