污染场地的健康风险不仅与污染物质对人体的危害特性有关，同时也与敏感人群的暴露途径和暴露浓度密切相关.在实际场地中，污染物浓度的分布常常存在着空间不均匀性(颜湘华等，2013)，另一方面，场地所处的气象气候因素、自然地理情况和水文地质条件也存在着空间变异性(Carsel and Parrish， 1988；Dagan，1989；Ptak and Teutsch， 1994；Zhang and Lu， 2002).同时考虑靠污染物在环境介质中迁移时不可避免的伴随着降解、吸附、稀释等作用，因此暴露浓度还存在着时间上的变异特性(Davis et al., 1991).因此，在进行场地污染风险评价时，必须合理考虑这种暴露浓度的时空变异性(不确定性)对人体健康风险的贡献.

文献研究表明，国内学者在对污染场地进行风险评价时，对风险的衡量通常只考虑病理方面的不确定性，即剂量-效应关系，而不考虑暴露浓度的不确定性.如国外普遍采用的场地污染风险评价模型RBCA和CLEA中(施烈焰等，2009；夏凤英等，2009；Chang et al., 2004)，将暴露浓度取为常数，并简单的用式(1)评价暴露浓度(Ferguson，2007)：

本研究通过对污染场地条件下，人体遭受致病或致死危害的全过程进行系统分析，建立了污染场地人体健康风险评价的全局模型.利用Monte Carlo方法和多孔介质溶质运移模型评价敏感人群的暴露风险，基于剂量-反应模型评价某一暴露剂量下，人群的致癌或非致癌风险.以重庆某重金属污染场地为例进行案例研究，利用假设检验方法确定污染物浓度的概率密度分布函数，基于多孔介质溶质运移模型和Monte Carlo方法计算场地的暴露风险，在此基础上利用剂量-效应模型评价场地的健康风险.

污染场地对人体健康构成危害的可能性和严重程度受3个过程及其相关参数影响：源(指污染源的浓度或浓度分布)，径(暴露途径及其参数不确定性)，以及汇(敏感人群的暴露剂量及剂量-效应关系).其中剂量-效应模型的研究目前较为成熟，本文主要关注对“源”和“径”过程及其相关参数不确定性的刻画，分述如下.

源强即场地中目标污染组分的浓度或浓度的概率密度分布.通常污染场地中污染物浓度在空间上并非均匀分布的，因此用一个特定的浓度值不能表征整个场地的真实污染水平.浓度的概率分布可以合理的描述场地的污染水平，表征源强不确定性对最终风险的影响.对某一污染场地，如果N个土壤样本的污染物含量分别为X1，X2，…，Xn，那么其概率分布可通过下述步骤计算.

对某些未检测数据和异常偏大数据进行处理，未检出值(No Detection，ND)用设备检测限(Limited Detection，LD)代替；异常偏大值采用Walsh′s Test方法进行识别和去除.

分别用常用的概率分布形态对样本数据进行拟合，并基于假设检验方法进行拟合优度检验，确定场地污染浓度数据的实际概率分布形态

暴露评估评价污染物从源到汇的迁移过程中，受气象因素、水文地质要素等不确定性的影响，人体暴露于某一浓度的概率.暴露评估基于多孔介质溶质运移机理和Monte Carlo方法，其中多孔介质运移模型模拟污染物在土壤和地下水中的迁移扩散，而Monte Carlo方法用以表征多孔介质运移模型中，各参数的不确定性对暴露浓度的影响，暴露评估的结果以暴露点污染物浓度的概率分布展现.Monte Carlo方法和多孔介质溶质运移模型的耦合过程见图 1.

图 1(Fig. 1)

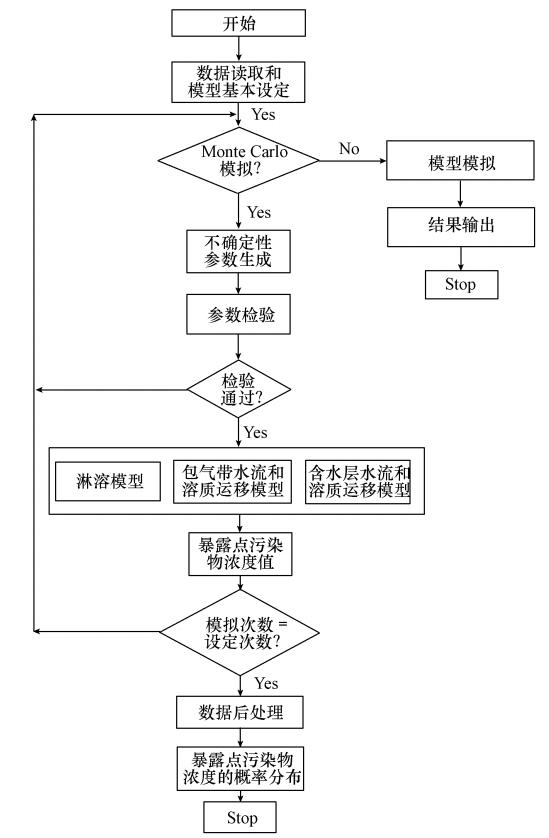图 1 Monte Carlo方法和溶质运移模型的耦合过程示意图 Fig. 1 The coupling process of Monte Carlo methods and solute transportation model

污染物在土壤中的迁移和转化的场景可以概化如图 2所示.整个暴露过程包含3个子过程：首先，在降雨淋溶作用下，污染土中的污染组分发生溶出和迁移，污染土中的污染组分浓度随之降低.第二个过程为淋溶污水在包气带中的运动迁移过程，包含有污染组分的淋溶液，在重力作用下垂直进入下方的干净土壤(即包气带)，最后经过包气带截污后进入到包气带下方的饱和含水层中，在饱和含水层中，污染物在对流和弥散作用下发生迁移和扩散，最终进入到取水井中，对人体健康构成潜在危害.

图 2(Fig. 2)

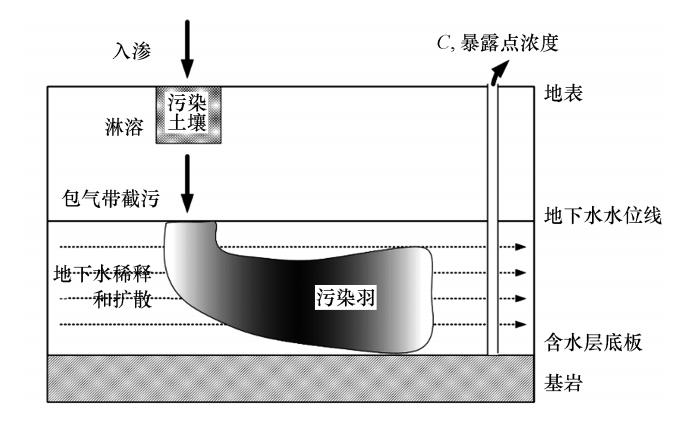图 2 污染组分在环境中的暴露过程示意图 Fig. 2 Exposure process of target contaminants

假定在任意时刻t，污染组分i在水相中的浓度C_L(t)是土壤中浓度C_w(t)的线性函数，即C_L(t)=K_w·C_w(t)，K_w为为液固分配系数(L · kg^-1).则污染组分i的浓度可以用式(2)表示(Hall et al., 2006)：

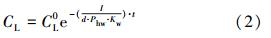
假设水流在包气带和地下水中的运动服从一维稳态方程，包气带和含水层中的溶质运移分别服从一维瞬态方程和平面二维瞬态方程，并考虑污染物的一阶降解和土壤的吸附解吸，可以分别得到污染物在土壤和含水层中的控制方程为(季文佳等，2010):

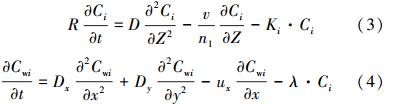
初始条件：浓度初值即为包气带和含水层中，各污染组分的背景值，因此初始条件可设为：

边界条件：对于包气带，其上边界为给定浓度边界，下边界为零浓度梯度边界：

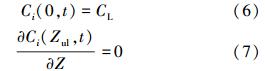
对于含水层模型，其边界条件为：

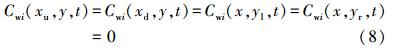
控制方程(3)和(4)，结合其约束条件(5)~(8)，可以用有限差分或者有限元法求得其数值解.

Monte Carlo模拟是目前解决风险评价中随机性和不确定性问题最为有效的方法之一(Denton et al., 2003).它可根据变量或参数已知概率分布值的重复计算来产生计算结果的概率分布，其核心原理就是采用服从某种分布形式的大量随机抽样来模拟可能出现的现象(Dahlgren et al., 2003).假定目标函数Y满足

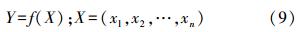
Monte Carlo模拟就是通过直接或间接抽样生成出每一随机变量的一个样本值，然后代入式(9)求出函数值Y，反复地独立模拟计算多次后得到函数Y的一组值Yl，Y2，…，Yn.当模拟的次数足够多时，就可由此来确定函数Y的概率特征.

暴露量计算采用式(9)(谌宏伟等，2006)：

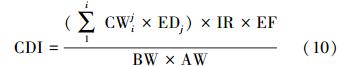
毒性评估分别考虑致癌效应和非致癌效应.致癌风险用风险值(Risk)表征，表示暴露于该种物质而导致的一生中超过正常水平的癌症发病率，当Risk大于10^-6时为不可接受风险.根据下式计算(夏凤英等，2009)：

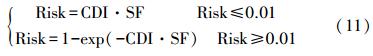
非致癌风险通常用风险指数(HI)进行描述，它定义为由于暴露造成的长期日摄入剂量与参考剂量的比值，当HI大于1时，风险不可接受.HI根据式(12)计算(陈鸿汉等，2006).

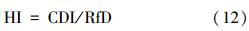
研究对象为我国西南地区某铬盐生产企业搬迁后的遗留场地，根据区域性规划该厂区在搬迁后将作为商住及公园绿化用地继续使用，为保证该区域开发后在其场地上生活、工作人员的身体健康，需要对该场地进行风险评价，并在此基础上进行污染治理和修复.研究区属亚热带季风性湿润气候，降雨丰富，厂区东侧紧邻嘉陵江，厂区地形总体起伏不大，地形坡度为10°左右，有利于地表及地下水的排泄.

场地污染调查采用分区域网格化动态布点方法，逐步细化确定铬污染程度和范围，最终完成287 个点位采样，获得1269 个土壤样品.土壤样品主要分析重金属Cr，其中w(TCr)(TCr 为总铬)按照HJ 491—2009《土壤总铬的测定火焰原子吸收分光光度法》测定，w[Cr(VI)]按照GB T 15555. 4—1995《固体废物六价铬的测定二苯碳酰二肼分光光度法》测定.

对污染物浓度的样本数据进行预处理，发现ND值2个，用LD值代替；通过Walsh′ test方法发现异常偏大值一个，结合场地条件进行分析后予以删除.对预处理后的数据进行概率分布形态拟合和假设检验，结果表明总铬和六价铬的浓度分布服从参数为(2291，46.4²)和(192，14.1²)的对数正态分布.

根据场地地形条件和水文地质条件，建立了污染物从“污染源-土壤-地下水-敏感点”过程的暴露评价概念模型.由于在厂区和嘉陵江之间进行了帷幕灌浆处理，因此截断了污染物向地表水源的扩散；同时根据实验分析，厂区主要污染物为Cr，不存在挥发性污染物，因此也不存在“土壤-空气-人体”这一暴露途径.另外企业搬迁后，利用建筑渣土对场地表层进行了覆盖处理，截断了厂区人群接触污染土的途径.因此主要的暴露途径是地下水暴露途径：在降雨淋溶作用下，Cr元素从浅层污染土壤中溶出，进入深层土壤，继而进入地下水含水层，在区域水力梯度作用下，顺着天然水流方向进入下游饮用水井中(如图 2所示).饮水井距离厂区边界1000 m.

暴露风险，即暴露点被污染的程度及对应概率，计算原理和方法如2.3节所述，利用多孔介质运移模型和Monte Carlo方法进行计算.模型所需参数及其概率分布函数如表 1所示.其中，下渗强度根据当地年降雨量、地形坡度、土壤类型，基于SCS曲线数法(Daniel et al., 2012)计算得到.

表1(Table.1)

表1 模型计算参数及取值 Table.1 Model parameters and their values

表1 模型计算参数及取值 Table.1 Model parameters and their values 参数 最小值(均值) 最可能值(均方差) 最大值 单位 分布类型* 注: *：N代表正态分布；S代表single；U代表Uniform分布；LT代表Log Triangle分布；LU代表Log Uniform分布；T代表Triangle分布. 污染土壤参数 下渗强度 113 380   mm·a-1 N   污染区域面积   2.0×105   m2 S 污染土壤深度 5   12 m U 污染土密度   1.3   kg·cm-3 S 液固分配系数   394.48   L·kg-1 S 包气带参数 厚度   5   m S 渗透系数 1.0×10-7 1.0×10-6 1.0×10-5 cm·s-1 LT 纵向弥散度 0.005   0.0065 m LU 孔隙度   0.5     S 含水层参数 厚度 25   35 m U 水力坡度 0.03 0.04 0.045   T X方向弥散度   0.005   m S Y方向弥散度   0.001   m S 渗透系数 1.0×10-4   5.0×10-4 cm·s-1 S 孔隙度   0.6     S

表 1所示参数中，下渗强度、污染区域面积、污染土层深度、污染土密度、包气带厚度、包气带和含水层渗透系数等参数已知其分布类型(郑春苗，2009)，根据其场地数据直接计算其统计参数；其他参数缺乏实测数据参考EPACMTP给出的推荐值(U.S EPA，2003).

将上述参数代入到模型中计算，得到观测井中任意时刻目标污染物浓度的概率分布.分别取5%、10%、50%、90%和95%分位值，表征最理想、较理想、正常、较不利和最不利情形下的污染物浓度，绘制其浓度历时曲线如图 3所示.从图中可以看出，井中六价铬和铬的初始浓度为零，随后逐渐增大，至第7年均达到最大值，随后逐渐减小.

图 3(Fig. 3)

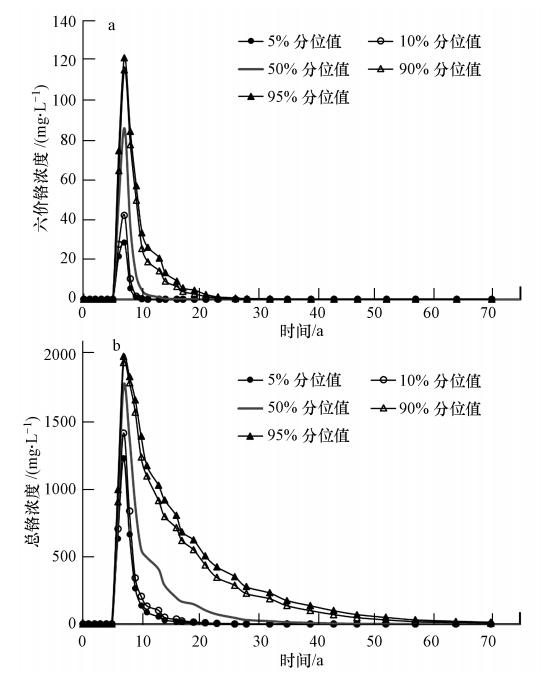图 3 暴露点处六价铬浓度和总铬浓度历时曲线 Fig. 3 Duration curve of Cr(Total) and Cr(VI)concentration at exposure point

现场调查显示以该水井为饮用水源的居民为14 户，人口总计40人(不考虑流动人口因素)，人均体重按60 kg计算，人均饮水量约为2 L · d^-1，暴露频率为365 d · a^-1，总暴露期取人类平均寿命70 a，平均暴露时间为25550 d.污染物中浓度分别取计算值的5%、10%、50%、90%和95%分位值(分别代表最理想、较理想、正常、较不利、最不利情形下的暴露剂量)进行计算.计算结果见表 2.

表2(Table.2)

表2 暴露剂量计算结果 Table.2 Computation results of exposure doses kg · kg-1 · d-1

表2 暴露剂量计算结果 Table.2 Computation results of exposure doses kg · kg-1 · d-1 元素形态 5%分位值 10%分位值 50%分位值 90%分位值 95%分位值 六价铬 0.0269 0.0391 0.0917 0.1970 0.2339 总铬 1.5350 1.9170 4.0757 9.3582 10.6703

最新研究表明总铬和六价铬经口摄入的危害性均为非致癌影响，其参考剂量分别为1.5和3.0×10^-3.根据式(12)计算正常情况下(50%分位数)总铬和六价铬的危害指数为30.57和2.72，均大于1，说明现状污染条件下，该场地将对附近生活的居民产生严重的非致癌风险.

考虑参数不确定性对风险评价结果的影响，分别采用表 2中的5%、10%分位值、90%和95%分位值作为暴露剂量进行计算，得到总铬和六价铬在最理想、较理想、较不利和最不利暴露情形下的健康风险值(见表 3).从表 3中可以看出，最不利情形下六价铬和总铬的风险值比正常情况下的风险值分别高出1.5倍和1.6倍.若以式(13)表征模型的不确定性系数，则本模型的不确定性系数为3~4左右.

表3(Table.3)

表3 不同暴露情形下的风险值计算结果 Table.3 Risk results under different exposure scenarios

表3 不同暴露情形下的风险值计算结果 Table.3 Risk results under different exposure scenarios 元素形态 各暴露条件下风险值 最乐观 较乐观 正常 较不利 最不利 六价铬 8.98 13.02 30.57 65.66 77.95 总铬 1.02 1.28 2.72 6.24 7.11

1)本研究采用多孔介质溶质运移模型描述场地污染物的迁移和扩散过程，基于Monte Carlo方法定量研究参数不确定性对暴露过程的影响，最终以概率的形式定量表征不同暴露情况出现的可能及相应的风险值，评价结果有助于风险管理者全面理解不同风险情况的出现概率，进而科学合理进行基于风险的污染场地管理和决策.

2)该场地在最乐观情形下，六价铬和总铬的非致癌危害商为8.98和1.02，高于可接受的非致癌危害商1；而在正常暴露条件下则高达30.57和2.72，这说明现状污染条件下，直接对该场地进行开发使用存在较大的健康风险，场地需要进行修复后使用.

3)通过对风险评价相关参数不确定性的定量化分析，得到最不利暴露条件下总铬和六价铬的非致癌危害商分别为77.95和7.11，大于正常情形暴露情形下的风险.这说明对场地进行污染风险评价时，需要审慎的考虑参数不确定性对最终风险后果的影响.