长江三峡工程运行后，水库发生泥沙淤积(Fang et al., 2000).由于污染物与泥沙颗粒的相互作用，包括营养物质及重金属在内的物质易在水库底部聚集.研究表明，三峡工程蓄水前，TN、TP入库负荷与出库负荷相等；而蓄水后，约84.45%的TN和48.76%的TP滞留于水库中(中国水利水电科学研究院等，2012).因此，研究泥沙颗粒与污染物之间的相互作用，认识污染物在天然水体中的不同赋存形式，成为三峡工程运行过程中亟待解决的一个重要科学问题.

泥沙颗粒与污染物之间的相互作用，即污染物在固/液两相之间的分配，通常称为吸附过程(汤鸿霄，1993).表面络合模型作为一种机理模型，自20世纪70年代初期被Stumm等(1970)首先提出后，被广泛应用于吸附过程的研究.早期的模型应用多针对纯矿物，尤其是水合氧化物.如Catts等(1986)应用表面络合模型研究了Cu、Pb和Zn在δMnO₂上的吸附特性；Dzombak等(1990)综合研究了水合氧化铁的吸附特性；Robertson等(1997)研究了pH值、离子强度等对不同氧化物吸附特性的影响.之后，表面络合模型被逐渐应用到天然泥沙颗粒.与纯矿物不同，天然泥沙颗粒是多种矿物的组合体，表面特性更为复杂.Wen等(1998)将泥沙颗粒视为整体，用平均表面官能团的概念研究了颗粒对Cu和Cd的吸附特性，发现表面络合模型也能较好地反应天然泥沙的吸附特性；Davis等(1998)则采用组分相加法，分别考虑组成泥沙颗粒的不同矿物成分，综合分析了Zn在颗粒表面的吸附特性；同样，Dong等(2012)研究了U(VI)在泥沙颗粒表面的吸附特性.

表面络合模型将颗粒物界面上与H⁺、OH^-和污染物等的结合用溶液中络合平衡的方式处理(汤鸿霄等，2000)，不同处在于考虑固液界面电荷的静电力影响，即基于某种双电层结构模式的假设，建立表面电荷与电位的定量关系，对表面络合常数加以静电力校正.常见的络合模型有恒定容量模式(CCM)、双层模式(DLM)和三层模式(TLM).前人多采用这些模型，对吸附过程做了较好的模拟.但这些模型均假设颗粒表面的电荷均匀分布，然后得到周围电位的分布规律(张中路等，1989)，进而对表面络合常数进行静电力校正.事实上，天然河流中的泥沙颗粒，除了包含多种矿物成分外，还具有极其复杂的表面特性，如表面形貌、晶体结构等，这些都导致颗粒表面电荷的非均匀分布(黄磊等，2012a).如何确定天然泥沙颗粒表面的双电层结构，是将表面络合模型应用到天然体系的又一大挑战(Davis et al., 1990).因此，考虑颗粒表面电荷的非均匀分布，对表面络合常数采用更合理的静电力校正，是本文的研究重点.

本文基于课题组已有的复杂泥沙的研究，考虑泥沙颗粒表面电荷的非均匀分布，修正传统的表面络合模型.首先，从泥沙颗粒形貌出发，结合表面电荷分布与形貌间的统计关系，构建统计意义下的颗粒表面电荷分布情况；然后，利用带电颗粒周围电位的计算公式，计算出表面电位的异质性分布，进而修正表面络合常数，得到非均匀电荷分布下的表面络合模型.修正模型更接近天然泥沙的吸附特性，对于水体中各种污染物在泥沙颗粒表面的吸附计算具有重要意义.

天然河流中的泥沙颗粒组成复杂，主要包括石英、长石及各种粘土矿物.在众多成分中，石英(SiO₂)所占比例最大，是天然泥沙的主要组成成分，如长江荆江段床沙中石英占79%~80%(钱宁等，1983).因此，本文以石英砂为例，展开相关研究.

取天然石英砂若干，过0.1 mm筛，储存在洁净的玻璃皿中，以供使用.试验时，将石英砂用导电胶布粘在金属样品盘上，然后放到扫描探针显微镜的样品操作台，进行表面形貌及电荷分布测量.整个过程要尽量地快，以减少外界环境对样品的污染.实验使用美国DI仪器公司生产的Dimension 3100型原子力显微镜，在清华大学物理系完成.

原子力显微镜(AFM)形貌测量采用接触模式在大气环境下进行成像观察，所有图像均在恒力模式下获得.这里对多个样品进行观测，每个样品至少进行3次不同位置的AFM观测，位置选取注重随机性，同时尽量保证每个位置具有不同特点，以提高其代表性.

静电力显微镜(EFM)电荷测量使用MESP探针，探针表面镀有一层导电金属膜.为了排除表面形貌对EFM信号产生的影响，首先利用AFM的表面成像功能，记录样品的表面形貌特征.然后，让探针回到扫描前的位置，并在竖直方向上抬高50 nm，使探针按照刚才记录的样品表面形貌特征，再进行1次开环扫描(Dianoux et al., 2003).这里对多个样品进行观测，观测位置的选择与形貌测量一样，注重随机性和代表性.

准确称取(0.4390±0.001)g磷酸二氢钾(分析纯)倒入1 L容量瓶中，加入去离子水配置成总磷浓度为100 mg · L^-1的磷标准液.取所需质量的石英砂在去离子水中配成悬浊液，泥沙浓度为10 g · L^-1；然后加入磷标准液配制所需浓度的总磷溶液，磷初始浓度分别为1.0、2.0、3.0、4.0、5.0、8.0和10.0 mg · L^-1；背景电解液为0.1 mol · L^-1 NaNO₃；在振动平台上振动24 h，达到吸附平衡.将悬浊液进行离心处理，提取上清液并过0.45 μm微孔滤纸，用钼酸铵分光光度法测定滤液中的总磷浓度.与此同时，制备空白样，做吸附前的磷浓度率定.由此计算出单位质量石英砂的吸附量(mg · g^-1).实验溶液pH为6~7，实验温度为室温，25 ℃左右.

颗粒物在水中结合配位水，成为羟基化的表面，即表面拥有大量的羟基官能团(Boehm，1971).这些表面羟基可以质子化或去质子化，也可以与溶液中的离子发生配体交换，具体过程如式(1)~(4)所示，其中，>S表示表面原子.将颗粒表面作为一种带有许多荷电表面羟基的聚合电解质，用类似溶液中络合平衡的方法处理颗粒物界面上与H⁺、OH^-和污染物离子等的结合.

表面质子反应：

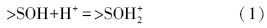
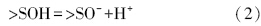
与溶液中离子的配体交换：

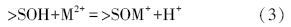
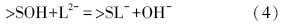
静电力校正项是表面络合模型区别于溶液中络合平衡的重要方面.欲求此校正项，则需了解在一定电荷密度σ₀下表面电位Ψ₀的情况.无论是恒定电容模式，还是双层模式或者三层模式，它们对颗粒表面双电层结构的假设，都是基于表面电荷均匀分布的概念，然后建立了不同的表面电荷与电位的定量关系，如表 1所示，其中，C、C₁和C₂为电容(F · m^-2)，I为溶液中的离子强度(mol · L^-1)，Z为正、负离子所带的电荷数，F为法拉第常数(C · mol^-1)，R为普适气体常数(J · K^-1 · mol^-1)，T为绝对温度(K)，下标0、β和d分别代表颗粒表面层、专属吸附离子层和扩散层.然而，天然泥沙颗粒的表面电荷并非假设的均匀分布，相反，复杂的表面结构(如晶体结构、矿物成分和表面粗糙等)都会引起表面电荷分布的异质性.Davis等(1990)指出，如何确定泥沙颗粒表面的双电层结构，是将表面络合模型应用到天然体系的一大挑战.下面我们将以石英砂为例，考虑颗粒表面电荷分布的异质性，提出非均匀电荷分布下的表面络合模型.

表1(Table 1)

表1 不同双电层结构模式下的电荷密度与电位关系 Table 1 Relationship between surface charge distribution and surface potential

表1 不同双电层结构模式下的电荷密度与电位关系 Table 1 Relationship between surface charge distribution and surface potential 恒定容 量模式 双层模式 三层模式 σ0=Cψ0 σ0=0.1174I1/2sinh(ZFψ0/RT) ψ0－ψβ=σ0/C1   ψβ－ψd=σ0+σβ/C2   σd=0.1174I1/2sinhZFψd/RT

图 1为石英砂颗粒表面的AFM形貌图像，扫描面积为2 μm×2 μm，给出了纳米尺度下颗粒的表面形貌.其中，图 1a为俯视图，图 1b为对应的三维图像.原子力显微镜的优点在于：不但图像的分辨率高，而且能够直接给出颗粒表面的高度值，为数据分析提供了方便.从图 1可以看出，石英砂颗粒具有极其复杂的表面形貌(如凸起、凹地、鞍部等)，且颗粒内部可能还存在着各种尺度的孔隙.这些复杂的形貌会导致颗粒表面活性位分布的异质性，引起颗粒与水体中污染物离子作用的不均匀，从而出现表面电荷的非均匀分布.

图 1(Fig. 1)

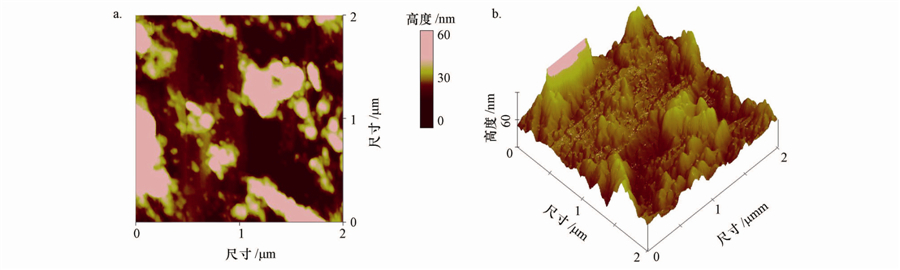图 1 石英砂颗粒的AFM图像(a.俯视图；b.三维图像) Fig. 1 AFM images of quartz s and (a.top view; b.3D image)

颗粒表面千变万化，形态各异，不可能用一个简单的函数式来描述.陈明洪等(2009)借用描述地球表面形态的理论来对颗粒表面形态进行研究.由于颗粒表面地形形态的不连续性，对表面形貌的描述采用分块处理的方法.假设颗粒表面上每个点P与其8-邻域点构成一个微曲面，根据微分几何的曲面论理论(梅向明等，1988)，设曲面参数方程为z=z(x，y)，其中，x、y为该点在图像矩阵中的坐标，则该点处的高斯曲率K和平均曲率H为：

图 2(Fig. 2)

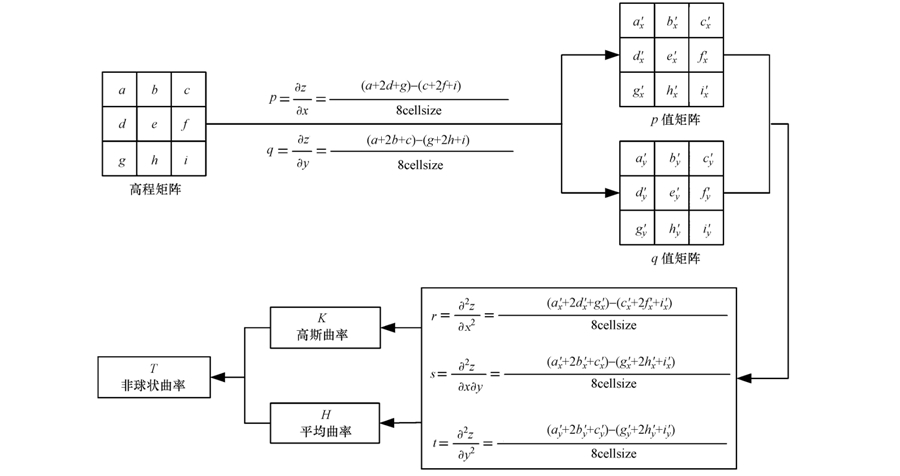图 2 表面曲率的计算流程图(Chen et al., 2013) Fig. 2 Calculation flow chart of surface curvature(Chen et al., 2013)

由于高斯曲率和平均曲率不方便单独用来判断地形特征，进一步引入非球状曲率T.它刻画了局部曲面形态与球体的接近程度，也是高斯曲率和平均曲率的函数.非球状曲率T的定义为：

图 3为静电力显微镜(EFM)测量得到的石英砂颗粒表面电荷分布(黄磊等，2012b).扫描面积为10 μm×10 μm，采样点数为256×256，采样点的间距约为39 nm，较为精细地在x、y方向上测量了石英砂颗粒的表面形貌与电荷分布状况.图 3a为形貌图，图中亮的区域表示该处的高程较高，暗色的区域表明该处的高程较低.图 3b为相位图，图中亮的区域相位差为正，作用力为斥力，由于该图是在导电针尖上施加+5 V电压时测得的，故该区域带正电，区域越亮电荷强度越强；反之，暗色的区域相位差为负，作用力为引力，该区域带负电，区域越暗电荷强度越强.

对比图 3a和b可以看出，石英砂颗粒表面电荷分布与表面形貌有一定的相关关系，表面形貌复杂的地方电荷密度相对较大.黄磊等(2012b)统计分析了电荷分布位置与颗粒表面微形貌的相关关系，认为电荷大多集中分布在颗粒表面的鞍部、凸起和凹地部位，而在凹槽、凸脊和平坦部位分布较少；此外，还统计了表面电荷与非球状曲率T的关系，即：

图 3(Fig. 3)

图 3 石英砂颗粒的表面形貌(a)与相位图(b)(针尖电压为+5V) Fig. 3 Surface morphology(a) and phase image(b)of quartz s and

图 4(Fig. 4)

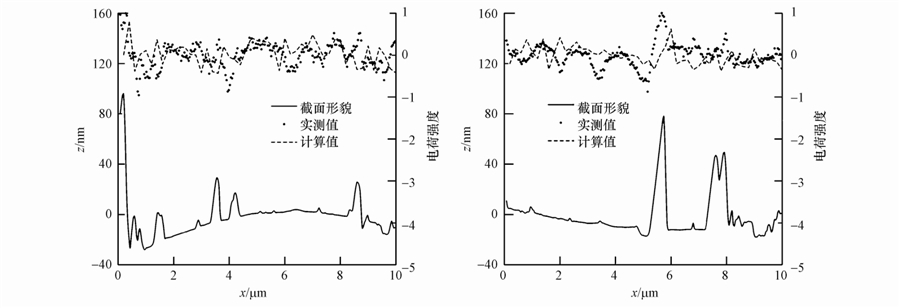图 4 石英砂颗粒表面电荷分布实测值与计算值的比较 Fig. 4 Comparison between the measured values and calculated values of surface charge distribution

前面给出了石英砂颗粒表面电荷分布的计算方法，对于任意一颗已知表面形貌的颗粒，利用式(7)及非球状曲率计算，可以得到其表面电荷分布.计算该电荷分布下的表面电位，则是修正传统络合模型，从而建立非均匀电荷分布下表面络合模型的关键.

非均匀带电颗粒周围电位的计算公式(Kirkwood，1934；Sader et al., 1998)如下所示：

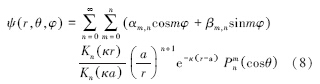
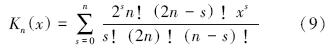
此外，系数 α_m，n和β_m，n 为表面电荷分布矩，对于具有N个离散点电荷的颗粒((r_i，θ_i，φ_i)处电荷值为q_i)，计算式如下：

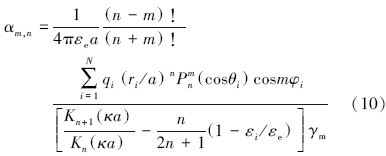
式(8)~(11)给出了非均匀带电颗粒周围电位的计算方法.令r=a，便可计算得到表面电位Ψ₀(a， θ，φ)的分布情况.由此，我们建立了颗粒表面形貌-电荷分布-表面电位三者间的数学关系，对于任意一颗已知表面形貌的颗粒，可以计算出其表面电荷分布，进而得到表面电位分布.

为了结果的代表性，即表面电荷分布-表面电位关系的代表性，我们观测了大量的石英砂颗粒，分别得到其表面形貌图.“数学泥沙”，即从大量颗粒形貌中抽象出的具有统计意义形貌的泥沙，是描述泥沙颗粒复杂形貌，研究其与污染物作用的重要工具(方红卫等，2009).借助构建数学泥沙的方法，本文建立了统计意义上的数学石英砂，具体如图 5所示.这样就可以建立统计意义上的表面电荷分布-表面电位关系，用于修正表面络合模型.图 6为数学石英砂表面电荷分布和电位分布的俯视图(电荷总量约为7.3×10^-13 C).

图 5(Fig. 5)

图 5 统计意义上的数学石英砂 Fig. 5 Mathematical quartz sand

图 6(Fig. 6)

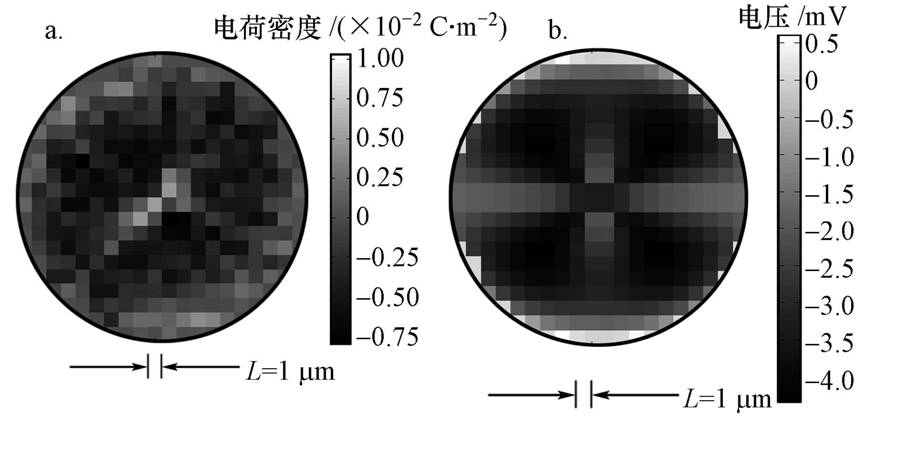图 6 数学石英砂表面电荷分布(a)与电位分布(b)的俯视图 Fig. 6 Surface charge distribution(a) and potential(b)of mathematical quartz sand

传统的表面络合模型，通过迭代求解质量作用方程与质量平衡方程，得到不同条件下污染物在固/液界面的分配情况.不同的模型假设不同的双电层结构，即不同的表面电荷与电位关系式，如表 1所示.考虑颗粒表面电荷的非均匀分布后，上述关系式不再适用.

3.1~3.3节建立了统计意义上的表面电荷分布-表面电位关系.在给定各组分初始猜想值的情况下(包括表面电位的猜想值Ψ^*₀)，根据体系中不同的界面反应，可以推求出颗粒表面的电荷总量Γ，它是由表面质子反应及与溶液中离子的配体交换引起的(式(1)~(4))，表达式如下：

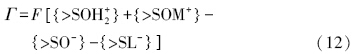
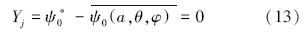
石英砂对磷的平衡吸附实验结果如图 7所示，实验pH为6~7.从图中可以看出，随着水相浓度的进一步增加，石英砂对磷的平衡吸附量逐渐增大；当水相浓度较小时，增长速度较快，平衡吸附量呈线性增长；而随着水相浓度的增加，平衡吸附量的增长速度逐渐变慢，最终趋于最大值，反映了石英砂颗粒对磷的最大吸附能力.这里，石英砂颗粒对磷的最大吸附量约为0.35~0.40 mg · g^-1.图 7同时给出了CCM、DLM及修正模型对实测数据的拟合情况，表面酸度常数取值为：logK_a1=-1.5，logK_a2=-7.5；其他参数选择如表 2所示.相比之下，修正模型考虑了石英砂颗粒表面电荷的非均匀分布，更接近实际情况，能够更好地模拟吸附结果.

图 7(Fig. 7)

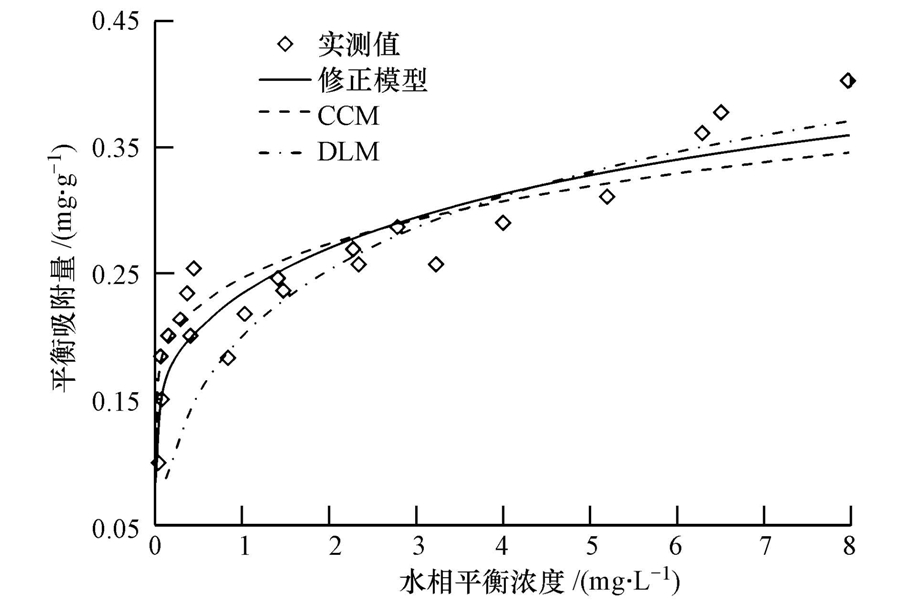图 7 石英砂颗粒对磷的平衡吸附 Fig. 7 Adsorption isotherm of phosphate on quartz sand

表2(Table 2)

表2 磷在石英砂颗粒表面吸附的参数选择 Table 2 Parameters for the adsorption of phosphate on quartz s and

表2 磷在石英砂颗粒表面吸附的参数选择 Table 2 Parameters for the adsorption of phosphate on quartz s and 模式类型 logK1 logK2 logK3 表面位密度/ (sites·nm-2) 电容C/ (F·m-2) 恒定容量模式 30.72 24.91 19.65 2.35 1 双层模式 29.00 24.91 19.65 2.35 - 修正模式 30.72 22.91 19.01 2.35 - >SOH+PO3－4+3H+=>SH2PO4+H2O logK1   >SOH+PO3－4+2H+=>SHPO－4+H2O logK2   SOH+PO3－4+H+=>SPO2－4+H2O logK3

为了更好地验证模型，本文采用他人的实验结果对修正模型进行进一步验证.Bolt(1957)在不同NaCl溶液浓度下对石英砂进行表面滴定实验，得到石英砂颗粒表面电荷密度随pH值的变化情况(图 8).从图中可以看出，石英砂颗粒表面电荷密度随着pH值的增大而逐渐减小，pH_pzc≈4.5；但不同NaCl浓度下，表面电荷密度变化的速度有所差异，离子浓度越高，变化越快.

图 8(Fig. 8)

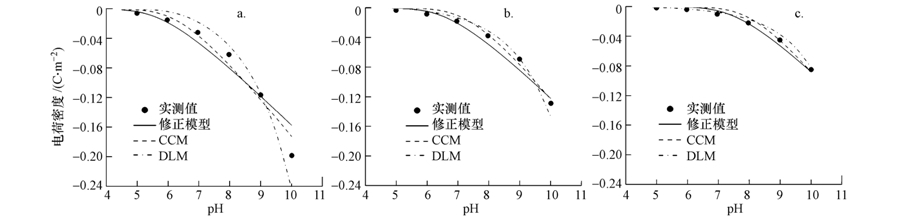图 8 不同NaCl溶液浓度下石英砂表面电荷密度随pH值的变化(a.0.1 mol · L-1，b.0.01 mol · L-1，c.0.001 mol · L-1) Fig. 8 Surface charges from Bolt(1957)for quartz s and in NaCl solutions(a.0.1 mol · L-1，b.0.01 mol · L-1，c.0.001 mol · L-1)

这里分别用CCM、DLM和本文修正模型对实测结果进行拟合(图 8)，其中，实心点为Bolt滴定实验结果，实线为本文修正模型计算结果，虚线和点虚线分别为CCM和DLM计算结果.各模式参数选择如表 3所示.由表可知，3种模式均能较好地再现实验结果，但修正模型由于考虑了石英砂颗粒表面电荷的非均匀分布，相比之下更接近天然泥沙的吸附特性，能够更好地模拟结果.

表3(Table 3)

表3 表面滴定实验中不同模式下的参数选择 Table 3 Parameters for the titration experiment

表3 表面滴定实验中不同模式下的参数选择 Table 3 Parameters for the titration experiment 模式类型 NaCl/ (mol·L-1) logKa1 logKa2 表面位密度/ (sites·nm-2) 电容C/ (F·m-2) 注: 1).参数的选择参照Sverjensky等(1996). 恒定容量 0.1 -1 -8 10 1 模式1) 0.01 -2 -9 0.001 -2.75 -9.75 双层模式1) 0.1 -1.5 -8.5 10   0.01 -1.2 -8.2 0.001 -1 -8 修正模式 0.1 -1.5 -7.5 10   0.01 -2.4 -8.4 0.001 -3.3 -9.3

Benyahya等(1999)研究了4种微量金属(Cd、Zn、Co和Mn)在石英砂颗粒表面的吸附，pH范围为4~9，结果如图 9所示(图中吸附量表示相对于最大吸附量的百分比，以便于不同数据的比较).实验中，石英砂浓度为1 g · L^-1，背景液为0.05 mol · L^-1 NaNO₃溶液，微量金属的初始浓度分别为：[Mn]=10 nmol · L^-1，[Co]=10 nmol · L^-1，[Zn]=50 nmol · L^-1和[Cd]=10 nmol · L^-1.从图中可以看出，微量金属在石英砂颗粒表面的吸附量随着pH值的增大而增加，当pH小于6时，吸附量很少，这时的吸附量可能主要来自阳离子交换量；当pH大于6时，吸附量随pH值的增大而快速增加.4种微量金属最大吸附量对应的pH值满足：Zn<Cd<Co<Mn.这里用修正模型对实验结果进行了拟合，模型参数如表 4所示.可见，该修正模型能够较好地模拟实测结果.

图 9(Fig. 9)

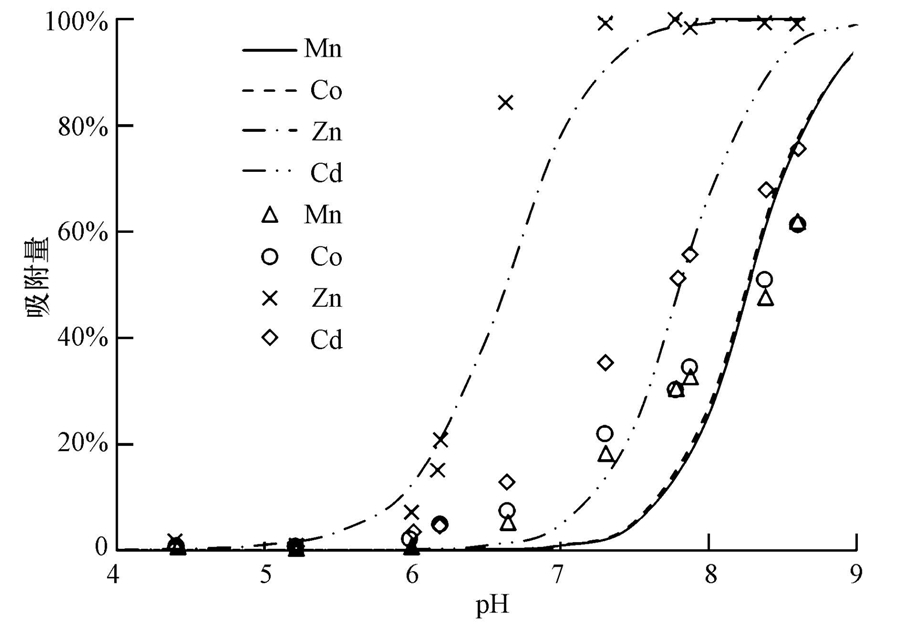图 9 Cd、Zn、Co和Mn在石英砂颗粒表面的吸附 Fig. 9 Adsorption of Cd，Zn，Co， and Mn on quartz sand

表4(Table 4)

表4 Cd、Zn、Co和Mn在石英砂颗粒表面吸附的参数选择 Table 4 Parameters for the adsorption of Cd，Zn，Co， and Mn on quartz sand

表4 Cd、Zn、Co和Mn在石英砂颗粒表面吸附的参数选择 Table 4 Parameters for the adsorption of Cd，Zn，Co， and Mn on quartz sand 重金属 logK logKa1 logKa2 表面位密度/ (sites·nm-2) Cd -5.57 Zn -3.73 -1.5 -7.5 2.35 Co -6.31 Mn -6.35 >SOH+M2+=>SOM++H+ logK

Subramaniam等(2003)研究了不同含沙浓度下Cu在石英砂颗粒表面的吸附，具体如图 10所示.石英砂浓度分别取0.25、1和2 g · L^-1，Cu的初始浓度为1.6×10^-4 mol · L^-1，背景液为0.001 mol · L^-1 NaNO₃溶液，表面位密度取值5.0 sites · nm^-2.图中线条为修正模型的拟合结果，表面酸度常数取值为：logK_a1=-1.5，logK_a2=-7.5；Cu的表面络合常数取值为logK=1.39.

图 10(Fig. 10)

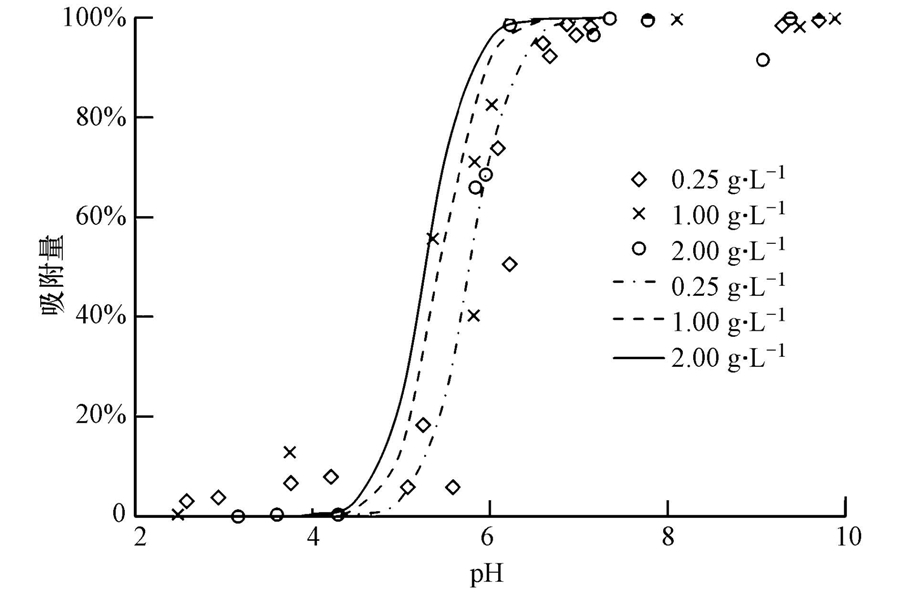图 10 不同含沙浓度下Cu在石英砂颗粒表面的吸附 Fig. 10 Adsorption of Cu on quartz s and under different s and content

1)石英砂颗粒具有极其复杂的表面形貌，这些复杂的形貌导致颗粒表面活性位分布的异质性，引起颗粒与水体中污染物离子作用的不均匀，从而出现表面电荷的非均匀分布.

2)表面电荷分布与表面形貌有一定的相关关系，可用来模拟颗粒表面电荷分布，进而结合非均匀带电颗粒周围电位的计算公式，建立表面电荷分布-表面电位数学关系.

3)利用统计意义上的表面电荷分布-表面电位数学关系，本文修正了传统的表面络合模型，并用表面滴定实验及吸附实验数据对模型进行验证.结果表明，修正模型考虑了泥沙颗粒表面电荷的非均匀分布，更接近天然泥沙的吸附特性.