2. 清华大学环境学院, 北京 100084;
3. 首都师范大学数学科学学院, 北京 100048
2. School of Environment, Tsinghua University, Beijing 100084;
3. School of Mathematical Sciences, Capital Normal University, Beijing 100048
河流、特别是流经人类活动对自然环境影响相对强烈区域的内陆河,是区域生态环境可持续发展的重要因素(Kowalkowski et al., 2006).作为区域居民生活污水、工业废水和地表径流排放的主要载体,内陆河最易遭受到污染和破坏(Singh et al., 2005).近几十年来,政府已经逐步建立了环境监测体系并且开展了大量水质监测项目,获得大量的水质监测数据,包括物理化学、有机物、重金属及生物指标等各种数据.由于各个监测指标及监测点之间存在复杂的相互影响,导致大量的监测数据并不能充分的利用与分析,给水质专家和地方决策者如何采取有效措施管理和改善水环境提出了一个挑战(Yang et al., 2010;Su et al., 2011;Xu et al., 2012;Wang et al., 2012).因此,从大量的环境监测数据中挖掘出有用的信息,探索水质的时空分布模式,识别潜在污染源能够提高人们对区域环境状况的认识,帮助决策者建立高效合理的水环境管理方案(Huang et al., 2010;Wang et al., 2013).
近年来,各类数学及统计评价方法被广泛用于水质评价、时空分异及潜在污染源识别的研究中.CCME WQI模型与其他水质指数模型相比具有简单易行、灵活多变等特点,对城市水体及水体富营养化污染尤其敏感,在水质综合评价中取得了令人满意的效果(Terrado et al., 2010;Akkoyunlu et al., 2012;Espejo et al., 2012).多元统计技术能够对复杂的多元数据进行降维简化又可以保证主要信息不会丢失,与近来被应用到多元数据信息挖掘的神经网络、平行因子分析等模型相比更为简便、普遍适应性广(Su et al., 2011).聚类分析、判别分析、主成分分析、因子分析和绝对主成分多元线性回归分析作为传统的多元统计技术,在水质时空分异特征及潜在污染源识别上得到普遍的应用(Bu et al., 2010; Yang et al., 2010; Akbal et al., 2011; Singh,2013).国内外学者利用多元统计技术分别对沁河流域(王翠榆等,2012)、洞庭湖(王丽婧等,2013)、土耳其中部近海(Akbal et al., 2011)、宁夏吴忠市金积水源地地下水(曹阳等,2013),以及德国北部低洼地区(Lam et al., 2012)的污染物时空分异特征及潜在污染源识别进行研究,并取得满意的效果.从研究进展上来看,数学及统计评价方法在时空分异特征及污染源识别的应用研究中仅仅局限于内陆河流域(Bu et al., 2010;张汪寿等,2012;李文赞等,2012)、湖泊(Yang et al., 2010;谢森等,2010)、近海海域(Akbal et al., 2011)及地下水(Singh,2013),却鲜有针对城市河网的水质时空分异特征及潜在污染源识别研究.与流域尺度研究不同,城市河网沿岸土地利用类型单一,不透水面护坡割裂了河道横向连通性,降雨径流冲刷地表直接将污染物携带入河(赵鹏等,2012),同时流域尺度水体的环境容量相对较大,水质空间分异有明显的上下游、干支流的关系,城市河网交错纵横,水流缓慢,人为干扰强烈,水质空间分异更为复杂;此外,以往的研究割裂开了时间与空间相互作用的机制,只是单独探讨了时间与空间上的分异特征及污染源识别,忽略了时间对空间分布规律及其污染源的影响(王翠榆等,2012).
苏州素有“上有天堂,下有苏杭”之美称,水系是其城市的命脉,水环境的好坏直接影响其作为旅游城市的可持续发展.因此,本文首先根据苏州古城区河网水质监测数据,应用CCME WQI模型对古城区河网水质进行综合的评价.然后采用聚类分析,揭示苏州古城区水环境时空相似性规律.并且利用空间判别分析验证聚类分析结果的可信度及识别显著性污染指标,最后在不同时间段内对空间分组进行时空联合因子分析并结合因子分析结果采用基于受体的源分配模型,识别不同时间段不同区域水环境污染源,以及主要污染源对河道水质的贡献,为苏州古城区水环境治理提供科学依据.
2 材料与方法(Materials and methods) 2.1 研究区概况苏州市地处以太湖为中心浅碟形平原的底部,位于北纬30°47′~32°20′,东经119°55′~121°20′之间,全市地势低平,自西向东缓慢倾斜(Mei et al., 2011);属于北亚热带湿润季风气候区,潮湿多雨,季风明显,具有丰富的雨水资源,平均年降雨量1200~1400 mm,降雨多集中于6—9月份(祁赛君等,2011).研究区为苏州市中心城区,面积大概为10 km2.监测断面多设在古城区,古城区内河道形成了“一环三横四纵”的水系布局.河道周边建筑密集,绿地和可渗透性地面相对较少,水体受潮水顶托与地形影响流向不定,流速缓慢,水体水质恶化严重,即便是水体流速较快的外城河、娄江、元和塘、上塘河等城区主要河道也均为Ⅴ类水质(吴蓓等,2007;官剑颖,2010;姜伟等,2012).造成水体污染的原因既有包括“三产”污染源及城市生活污染源在内的点源污染,也有城市降雨径流及河道底泥释放引起的非点源污染(吴蓓等,2007;严以新等,2008;官剑颖,2010).
研究区河道水质监测断面30个(图 1),苏州市排水管理处每月一次取样检测.监测断面M1~M30依次为保吉利桥、苑桥闸、望星桥、马津桥、平四闸、桃花坞桥、水关桥、中市桥、带城桥、银杏桥、小人民桥、歌薰桥、醋坊桥、跨塘桥、齐福桥、钱万里桥、糖坊湾桥、觅渡桥、裕棠桥、泰让桥、渡僧桥、山塘桥、吊桥、新市桥、人民桥、相门桥、永仙桥、五龙桥、桐馨桥、永津桥.
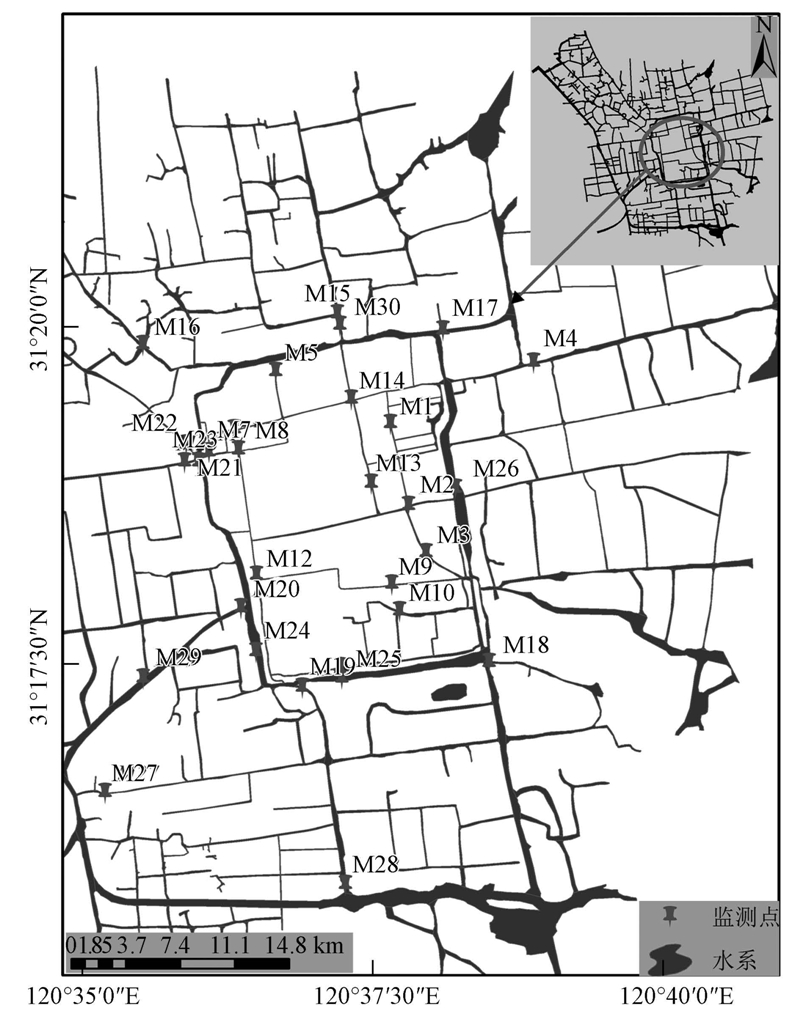 |
| 图 1 研究区位置及监测断面分布图 Fig. 1 Location map of study area and distribution of monitoring sites |
数据来源为古城区2012年30个监测断面相关数据,11个指标包括总氮(TN)、氨氮(NH3-N)、总 磷(TP)、溶解氧(DO)、浊度(Turb)、pH、水温(T)、高锰酸盐指数(CODMn)、电导率(EC)、藻密度(Algae density)、叶绿素(Chl).每月监测1次(12月份数据除外),共3630个(30×11×11)监测样本,所有样本的采集及检测分析严格按照地表水环境质量标准(GB3838—2002)中的方法进行实验室分析,具体结果统计描述见表 1.
| 表1 水质指标的统计描述及环境标准 Table 1 Statistical description of water quality variables and the environmental guideline of national quality st and ards for surface waters |
总体上,苏州古城区的水环境污染相当严重.TN、NH3-N、TP、DO、CODMn均值分别为4.99、3.14、0.38、3.64、4.90 mg · L-1,地表水环境质量标准中相应指标Ⅴ类水标准分别为2.0、 2.0、0.4、2.0、15.0 mg · L-1.TN为Ⅴ类水标准的2.5 倍,NH3-N为1.2 倍,TP则接近于Ⅴ类水标准,DO则属于Ⅳ类水质,CODMn属于Ⅲ类水质.
2.3 研究方法 2.3.1 CCME WQI模型CCME WQI模型(CCME,2001;Terrado et al., 2010;Akkoyunlu et al., 2012)由加拿大环保部开发,该水质指数与其它水质指数相比具有运算简单、参数设定可以结合研究区水质保护提升目标而设定的特点(Terrado et al., 2010).模型根据输入水质监测数据将采样点水质归一化到0到100之间,并根据水体污染的程度,从0~100将水质由差到极好划分为5类,分别对应差(0~44):水环境遭到持续性的威胁和破坏;及格(44.1~64):水环境遭到频繁的威胁和破坏;一般(64.1~79):水环境偶尔遭到威胁和破坏;好(79.1~94):水环境得到保护只是遭到小范围的威胁和破坏;极好(94.1~100):水环境得到完善的保护.具体计算公式为:
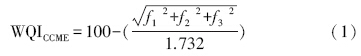
苏州古城区河网水体氮、磷指标已经超过地表水Ⅴ类水标准.因此,本文短期内将地表水环境质量标准的Ⅴ类标准作为模型的水质提升目标,同时根据苏州古城区水质监测数据和地表水环境质量标准(GB3838—2002)将TN、NH3-N、TP、DO、pH、CODMn作为WQI计算所需的监测指标.对古城区各个河道的水质污染程度进行综合评定.
2.3.2 层次聚类分析聚类分析(CA)是根据对象距离远近或相似性大小进行分类的多元统计方法.本文采用的层次聚类分析(HCA)是应用最广泛的聚类方法,该法以逐次聚合的方式将距离最近或者最相似的对象聚成一个类簇,直至最后聚成一类(Lattin et al., 2003;陈彦光,2011).本文采用的计算方法是欧氏距离平方和离差平方法.此外,该方法具有探索性,所以,还采用其它方法进行验证(Lattin et al., 2003).
聚类分析要求数据符合正态分布,在进行分析之前,需要利用K-S非参数检验(Shrestha et al., 2007)分别对月平均和采样点平均数据组进行正态检验.结果显示,月平均数据组各监测指标除DO外均以95%或更高的可信度服从正态分布;采样点平均数据组各指标偏离正态分布,进行自然对数转换后(Shrestha et al., 2007;李文赞等,2012),各监测指标除T、CODMn和Chl外均能够以95%或更高的可信度服从正态分布.为了消除变量单位量纲的影响,同时需要对数据进行标准化处理(均值为0,方差为1).
2.3.3 判别分析判别分析(DA)是多变量统计分析中用于判别样品所属类别的一种统计分析方法.可以用来判别CA分析结果和识别显著性的污染指标.此方法分为3类:标准式、前进式和后退式.相比之下,后退式DA方法具有更好的指标降维能力和判别能力(Shrestha et al., 2007;周丰等,2007).所以,本文利用后退式DA方法对原始数据进行时空差异性分析,并采用交叉验证法(Cross-validation)检验此方法的判别能力.相应的判别函数表达式如下:
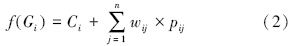
因子分析(FA)是一种既可以降低变量维数,又可以对变量进行分类的广泛应用的方法(Davis,1973;卜红梅等,2009).其实质是从多个实测的原变量中提取出较少的、互不相关的、抽象综合指标,即因子.每个原变量可用这些提取出的公共因子的线性组合表示,具体参见公式(3).同时,根据各个因子对原变量的影响大小,也可将原变量划分为等同于因子数目的类数.在水质分析中,此方法主要用于提取污染因子和识别污染源(Su et al., 2011;王翠榆等,2012;Lam et al., 2012).
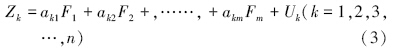
因子分析要求变量间要有一定的相关性,所以在数据分析之前需要利用巴特莱检验(KMO)(Shrestha et al., 2007)检验数据应用因子分析的可行性.同时,考虑到水质指标数量级上的差异,需要对数据再进行标准化(均值为0,方差为1).一般来说,分析结果只选取特征值大于1的因子(Bu et al., 2010;王翠榆等,2012).因子分析及判别分析均采用原始数据.
2.3.5 APCS-MLR绝对主成分多元线性回归分析法(APCS-MLR)是一种基于因子得分,评价各个因子对各个变量贡献的统计方法.其原理是将变量值与因子得分进行多元线性回归,根据回归参数得到针对各个因子的估计值,从而确定因子对各个变量的贡献,具体参见公式(4)(Miller et al., 2002).目前,这种方法在水质评价中用于计算污染因子对各个评价指标的贡献率(Zhou et al., 2007;瞿明凯等,2013).

研究中多元统计分析及水体综合水质空间分析采用的是Microsoft Excel 2007、SPSS19和ArcGis9.3.
3 结果与分析(Results and analysis) 3.1 CCME WQI水质综合评价水质综合评价显示(表 2),苏州古城区河道水质相对于地表水Ⅴ类水质标准,CCME WQI值介于40~74之间,有66.67%的监测点水质处在差和及格状态,而剩下33.33%的监测点水质处在一般状态,说明苏州古城区河道水质污染普遍严重.
| 表2 CCME WQI评价结果 Table 2 The result of CCME WQI |
从图 2可知,古城区内城河河道污染程度要比外围河道严重,这可能与古城区内部和外部人口密度存在差异,餐饮旅游主要集中在古城区内,以及古城区内城河道水体流动性相对缓慢有关.
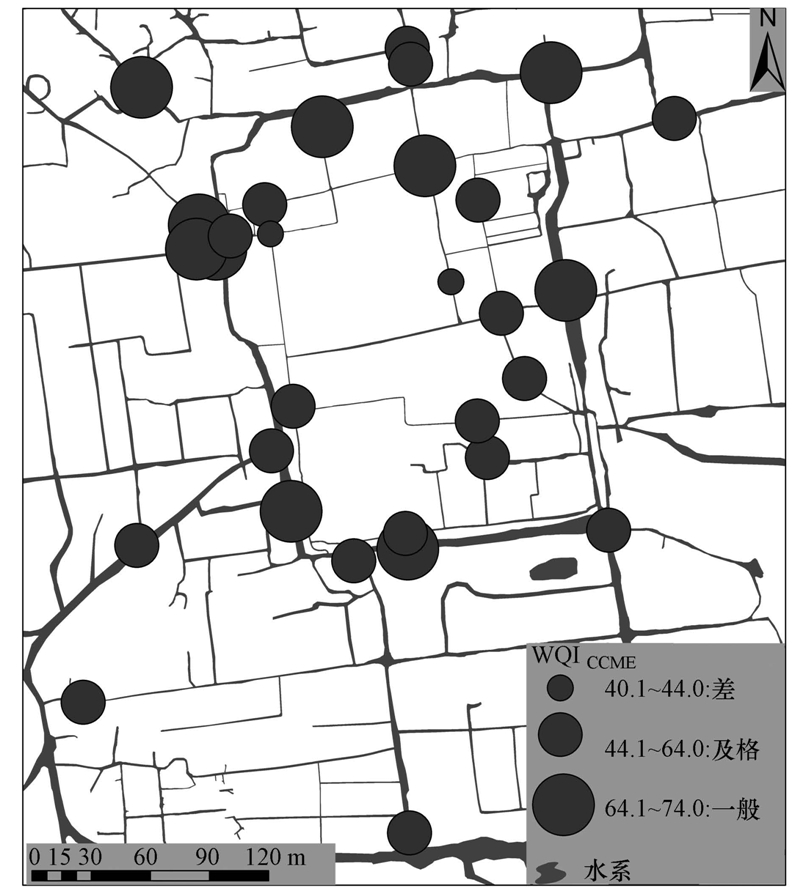 |
| 图 2 CCME WQI采样断面空间分布图 Fig. 2 The spatial distribution of CCME WQI |
时间尺度聚类分析与判别分析结果表明:全年可分为3个时段(图 3),时段Ⅰ(1—3月)、时段Ⅱ(11月、4—6月)和时段Ⅲ(7—10月),水体污染程度由重到轻依次为时段Ⅰ、时段Ⅱ、时段Ⅲ.时间聚类结果的判别分析交叉验证正确率(表 3)达到88.1%,表明全年分3个时段是比较合适的.判别函数(表 4)用了7个监测指标:TN、TP、DO、T、CODMn、藻密度、Chl,体现古城区河网水质的时间差异性规律.从苏州古城区水体污染物时间尺度的差异性图(图 4a)中可以看出总体上、时段Ⅰ、时段Ⅱ和时段Ⅲ,TN、TP、DO和CODMn随着时间的推移浓度在逐渐减少.同时,T 及藻密度和Chl随着时间的推移逐渐在升高.
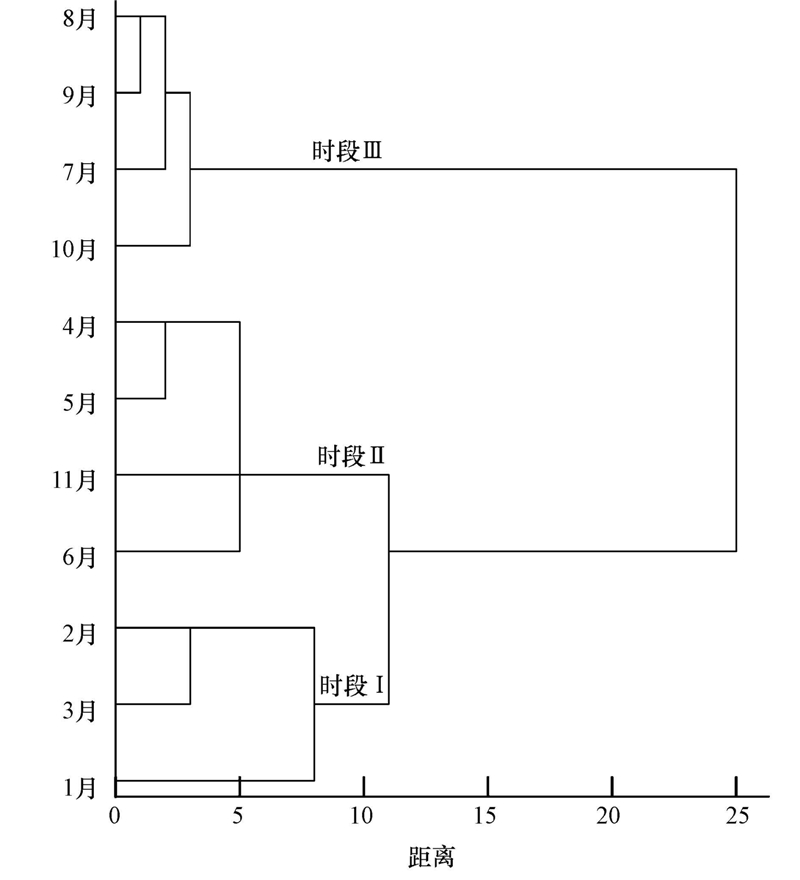 |
| 图 3 苏州古城区水体污染物的时间尺度聚类分析 Fig. 3 Temporal cluster analysis of pollutants in ancient town of Suzhou |
| 表3 苏州古城区水体污染物的时空判别分析 Table 3 Spatial and temporal discriminate analysis of pollutants in ancient town of Suzhou |
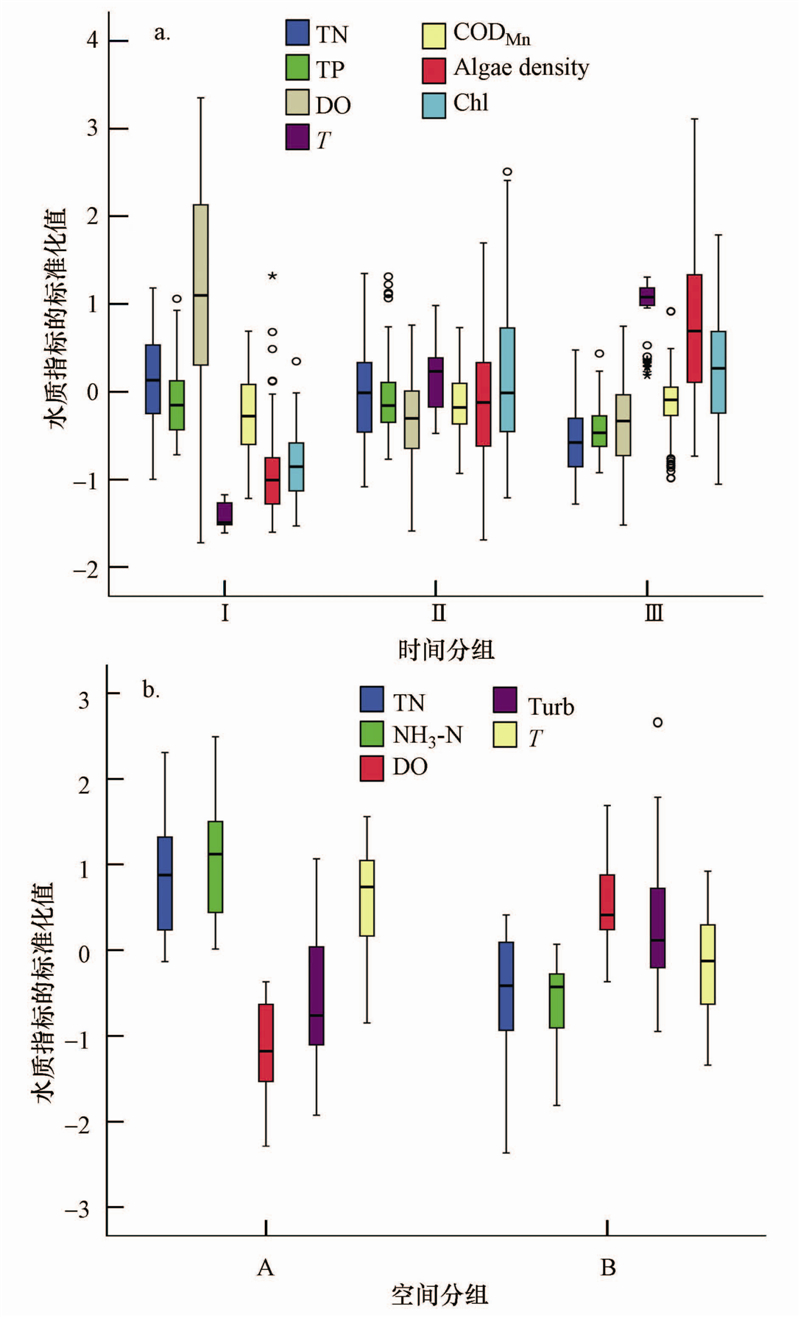 |
| 图 4 苏州古城区水体污染物时间尺度(a)和空间尺度(b)的差异性 Fig. 4 Temporal and Spatial variation of pollutants in ancient town of Suzhou |
苏州的雨季主要集中在6—9月份(祁赛君等,2011),从时间聚类结果可以看出,6月份古城区水体的TN、TP、CODMn浓度并没有因为降雨量的增加而减少,到了7月份才开始有所下降,说明雨季初期苏州古城区河道除了受到来自城市生活及餐饮旅游等“三产”污水的点源污染外,还可能受到来自地表径流及河道底泥释放的非点源污染.雨季在9月份底进入尾期,从聚类结果看出,10月份的降雨量已经锐减而却被聚到第3类(时段Ⅲ),相应的11月份没有归并到第1类(时段Ⅰ),而被归并到第2类(时段Ⅱ),可能说明雨期降水对河道污染物的稀释作用在一定程度上改善了河道水质.
上述现象表明:按照流域水质评价常用的根据旱季和雨季或者4个季度来进行城镇的水质评价和污染控制不能体现城镇水体污染的特殊性,不能真正揭示和把握城镇水体污染在时间序列上分异特征;由于城镇河道周围大量的不透水面导致降雨径流直接携带大量的污染物进入河道,所以在雨季前期(5、6月)就应该开始采取流域面源控制措施,以减轻降雨高峰期的非点源污染控制压力;同时雨季过后,应当将防治重点转移至点源控制,以减少河道内源污染物的积累(王翠榆等,2012).
3.2.2 污染特征的空间相似性与差异性空间尺度的聚类分析和判别分析表明:空间上可以将采样点分为2组(图 5),第1组(A组)主要位于古城区内城河,分别为保吉利桥、望星桥、桃花坞桥、中市桥、带城桥、银杏桥、小人民桥、醋坊桥、水关桥、歌薰桥;第2组(B组)主要位于外城河及进出外城河河道,分别为苑桥闸、苑桥闸、跨塘桥、钱万里桥、糖 坊湾桥、山塘桥、吊桥、相门桥、平四闸、齐福桥、觅渡桥、裕棠桥、泰让桥、渡僧桥、新市桥、人民桥、永仙桥、五龙桥、桐馨桥、永津桥.采样点聚类分析结果的判别分析交叉验证(表 3)正确率达到78.5%,误判的区域主要集中在古城区外城河和内城河的连接河段,总体分类结果较好.
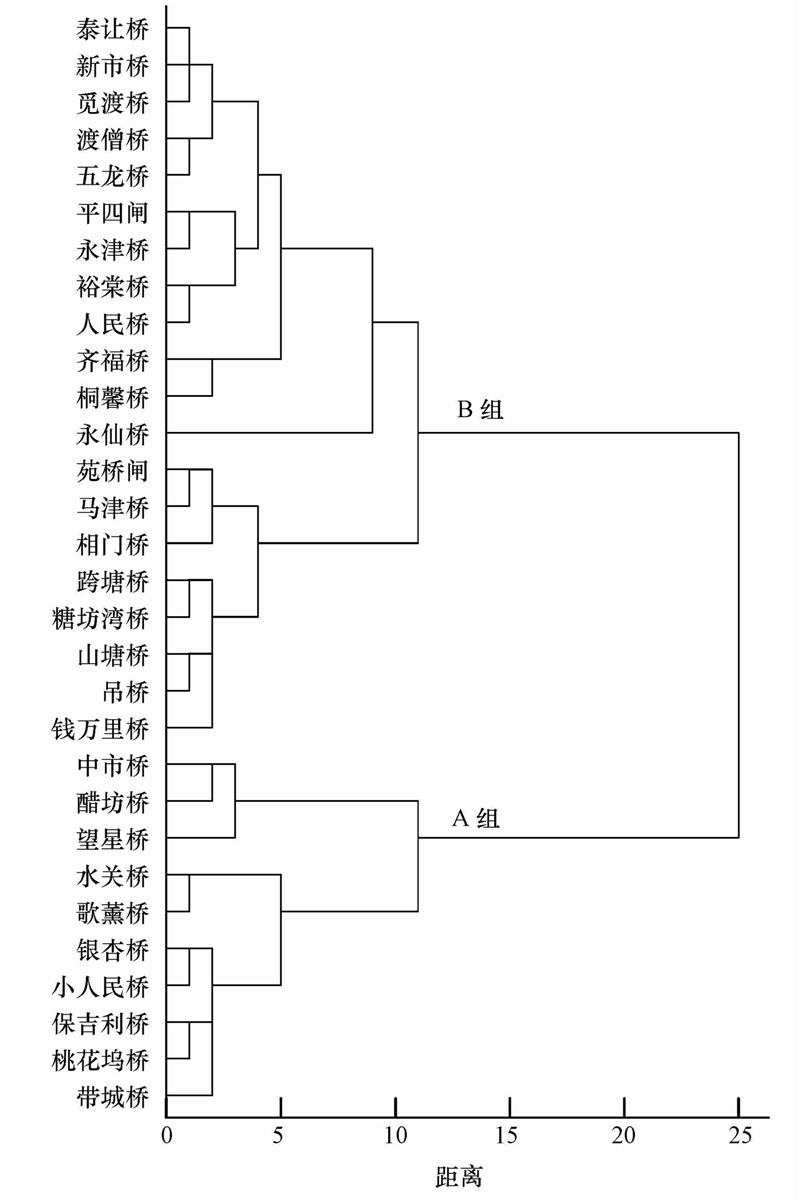 |
| 图 5 苏州古城区水体污染物的空间尺度聚类分析 Fig. 5 Spatial cluster analysis of pollutants in ancient town of Suzhou |
对采样点聚类结果的判别分析(表 4)用了5个指标:TN、NH3-N、DO、浊度和温度,体现古城区河网水质空间差异性规律.从苏州古城区水体污染物空间尺度的差异性图(图 4b)中可以看出,总体上,第1组(A组)即古城区内城河河道污染较为严重,主要体现为含氮污染物的污染.相对于外城河,古城区内城河河道的平均水温要较外城河河段高出0.2 ℃.这可能与古城区内建筑密集、人口密度大,以及当地人民历来的生活习惯、家庭生活用水直接就近排放到河道内的现象有关;古城区内城河水体的溶解氧浓度明显低于外城河,为2.63 mg · L-1,属于国家地表水Ⅴ类水标准.这可能与苏州市古城区以平原地形为主,河底高程和水流坡降较小,古城区内河道水流长年滞流,水体复氧能力差有关(严以新等,2008).
| 表4 苏州古城区水体污染判别分析的典型变量及其系数 Table 4 Classification functions for discriminant analysis of pollutants in ancient town of Suzhou |
综上所述,苏州水环境治理主要集中在古城区内城河,可以通过控源截污、河道疏浚、水系沟通、引清入渠等多种举措治理改善内城河水质污染严重的现象.
3.3 时空联合因子分析与污染源解析利用时间聚类结果判别分析所建立的判别函数对不同聚类分组进行判别验证,发现时段Ⅰ、时段Ⅱ、时段Ⅲ的判别正确率分别为98.9%、84.9%、83.2%,总判别正确率为88.1%;空间聚类结果判别分析所建立的判别函数对不同聚类分组进行判别验证,发现类别A、类别B的判别正确率分别为64.8%、83.5%,总判别正确率为78.5%(表 3).说明同一区域在不同时间段或者同一时间段内不同区域的水质污染分布规律存在明显差异.同时,从苏州市古城区水体污染物各空间分组在各时段的空间差异图(图 6)可以看出,空间分组A和B在不同的时间段内的污染物水平有着较大的差异.因此,有必要将时间及空间聚类分析结果有机结合,对不同区域在不同时段下的污染源进行解析,为水环境管理和改善提供更为详尽的理论依据.
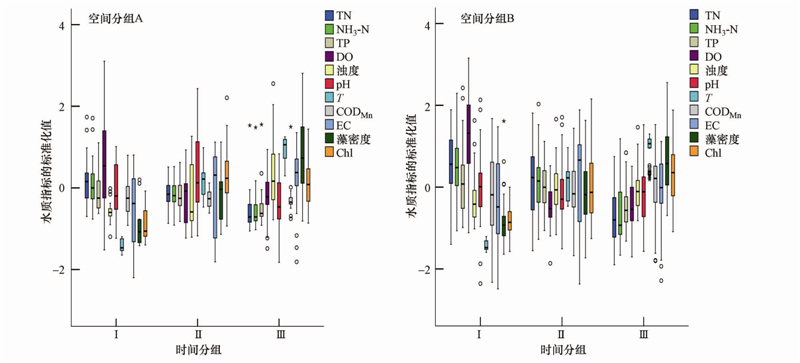 |
| 图 6 苏州中心城区水体污染物各空间分组各时段的空间差异性 Fig. 6 Spatial variation between periods of pollutants in ancient town of Suzhou |
根据特征因子大于1的原则(Bu et al., 2010;王翠榆等,2012)对空间分组A在时段Ⅰ、时段Ⅱ和时段Ⅲ分别提取4、3和4个因子(最大方差旋转),累计解释方差83.64%、72.67%和77.98%(表 5).
| 表5 时空联合因子分析因子旋转载荷矩阵 Table 5 Loadings of 11 variables on significant principal components for spatio-temporal Factor Analysis |
在A组-时段Ⅰ:F1的方差贡献率为46.34%,表征因子为TN、NH3-N、TP、DO、T、CODMn和EC,除DO外都呈现正相关,同时由表 6可知,TN、NH3-N、TP、CODMn之间有显著相关性,Pearson相关系数都在0.8以上,表明F1代表着城市生活及餐饮旅游等第三产业污水的营养物质及耗氧有机物污染;F2的方差贡献率为16.56%,表征因子为藻密度和Chl,并且与T之间存在显著的相关性.表明F2代表着自然因素水温对古城区内城河富营养化程度的影响.古城区生活及“三产”污水排入河道,导致水体营养物质过剩,在水温的年内变化的作用下,导致藻类的大量繁殖.F3的方差贡献率为11.45%,表征因子为浊度.F4的方差贡献率为9.29%,表征因子为pH.
在A组-时段Ⅱ:F1的方差贡献率为43.46%,表征因子为TN、NH3-N、TP、浊度和CODMn、DO,除DO外都呈正相关.与在A组-时段Ⅰ基本一致,不同的是浊度在第一因子中占有较大的载荷,可能与时段Ⅱ降雨的增加,降雨径流携带大量的悬浮物进入河道,以及降雨对河道底泥的扰动有关.F2的方差贡献率为19.93%,表征因子T和藻密度呈正相关,且与pH呈现负相关.从表 6可以看出,T跟藻密度、Chl存在显著的正相关性,pH跟藻密度负相关.
| 表6 污染指标间Pearson相关系数 Table 6 Pearson correlation coefficient between water quality variables |
F3的方差贡献率为9.48%,表征因子为Chl和EC,与pH呈现负相关.F2和F3表明自然因素水温对河道水体的影响.大量的营养物质及耗氧有机物随着生活及餐饮旅游等第三产业污水排入河道,在水温逐渐升高的作用下,藻类开始大量生长,水体中积累过多的有机物消耗水体中的溶解氧,使得水体中的溶解氧减少,乃至出现厌氧环境,进而促使氨和有机酸的形成,这些酸性物质的水解最终导致pH值下降(Shrestha et al., 2007).统计可知,从时段Ⅰ到时段Ⅱ内城河河道藻类的平均密度由1009.78 cells · mL-1增长到1564.79 cells · mL-1,pH以一定的幅度在减小.
在A组-时段Ⅲ:F1的方差贡献率为39.33%,表征因子为TN、NH3-N、TP和CODMn,与DO呈一定的负相关,与时段Ⅰ类似.F2的方差贡献率16.57%,表征因子为T、藻密度和Chl,且呈正相关,与pH呈负相关,与时段Ⅱ类似.F3的方差贡献率12.54%,表征因子为DO和EC.F4的方差贡献率9.54%,表征因子为浊度和pH.苏州古城区在时段Ⅲ和时段Ⅰ、时段Ⅱ一样,主要受到生活污水的污染及耗氧有机物污染,不同的是,随着温度的进一步升高,藻类大量的繁殖达到顶峰,由时段Ⅰ到时段Ⅲ的平均藻密度由1009.78 cells · mL-1增长到了2076.74 cells · mL-1,与此同时pH值由7.24降到7.17.
综上,大体上古城区在不同的时间段主要受到生活和餐饮、旅游“三产”污水的污染,但局部有所差别,在时段Ⅱ第一主成分在浊度上具有较高因子载荷,说明有可能在时段Ⅱ内城河河道同时受到降雨地表径流、河道底泥释放的非点源污染;同时,在时段Ⅰ受限于水温的影响,藻类的繁殖得以抑制,随着温度的升高,藻类开始大量繁殖,对水生环境造成严重的影响.建议在冬季对河道底泥进行清淤,可以一定程度上起到抑制藻类生长的效果(邢雅囡等,2006).
3.3.2 空间分组B各时段因子分析由于空间分组B各时段在因子分析前的巴特莱检验KMO低于0.6,不适合在各时段内分别做因子分析(Shrestha et al., 2007),只对空间分组B做全年的因子分析(方差最大旋转),根据特征值大于1的原则提取了3个因子,共解释了62.28%的总方差.
F1的方差贡献率31.37%,表征因子为TN、NH3-N、TP和CODMn,代表营养物质和耗氧有机物污染,主要来自城市居民生活及餐饮旅游等第三产业污水的排放.F2的方差贡献率20.36%,表征因子为DO、T、藻密度和Chl,DO与T、藻密度和Chl呈负相关,T与藻密度和Chl呈正相关,代表生物化学污染,主要来至自然因素与人为排放的营养物质相互作用造成水体富营养化污染进而导致藻类爆发.F3的方差贡献率10.55%,表征因子为EC.
3.3.3 绝对主成分多元线性回归(APCS-MLR)依据因子分析,内城河在时段Ⅰ、时段Ⅱ和时段Ⅲ及外围河道在全年时段内主要受到TN、NH3-N、TP、CODMn、DO和T等指标的影响,故对内城河及外围河道在全年时间段内进行污染源分配研究.由表 7可知,除浊度、pH、DO、EC和Chl的R2较小外,其余都在0.6以上,说明回归分析有统计学意义(Miller et al., 2002).此外估计值与实测值的比值(E/O)在0.994~1.143之间,也证明了这一回归结果的准确性(卜红梅等,2009).通过APCS-MLR得到的污染源贡献率可能为负值,也可能大于100%,这与污染源的排入对其他非影响指标的稀释有关(Miller et al., 2002).由表 7可知,古城区内城河F1对TN、NH3-N、TP和CODMn的贡献率分别为25.09%、31.81%、34.12%、19.83%,表明TN、NH3-N、TP和CODMn来自城市生活及餐饮旅游等第三产业污水.同时,F1只是部分解释了TN、NH3-N、TP和CODMn的来源,表明古城区人为干扰强烈,污染源更为复杂,未识别的污染源可能来自地表径流或河道底泥的扰动(吴蓓等,2007;严以新等,2008).F2对DO的贡献率为88.27%,表明DO主要受到生物化学污染影响.古城区外围河道及内外连通河道F1对TN、NH3-N、TP、CODMn和EC的贡献率分别为59.68%、81.31%、24.20%、13.92%.F2对TN、NH3-N和DO贡献率分别为11.01%、14.27%、35.79%,F3对TN的贡献率32.92%.表明TN、NH3-N、TP、CODMn同样是来自城市生活及餐饮旅游等第三产业污水.
| 表7 公因子对各个指标的贡献率 Table 7 Source contribution for each variable |
1)通过CCME WQI评价模型计算结果可知,内外城河CCME WQI值介于40~74之间,其中,66.67%的监测点水体污染较严重,水环境系统遭到破坏,主要集中在内城河河道.
2)时间尺度上将全年聚类为3类,分别对应1—3月、11月及4—6月、7—10月.水质状况从时段Ⅰ、时段Ⅱ到时段Ⅲ逐渐在改善;雨季初期河道水体的氮、磷污染物含量在增加,说明古城区河道除了受到生活及“三产”污水的点源污染以外,还可能受到降雨地表径流和底泥释放的非点源污染.
3)空间尺度上将水质监测点分为2组,分别对应古城区内城河,外城河和内外连接河道.与古城区外围河道相比,古城区内,城中村多、人口密集、餐饮旅游点多,过去没有安装地下分流截污管道;餐饮企业厨余污染、游客丢弃垃圾及居民生活污水未接纳管网,污染源分散;另外,内城河河道狭窄、流速缓慢、河道底泥深厚,导致古城区水体污染要较外城河及进出外城河河道要严重.因此,苏州水环境治理主要集中在古城区内城河.
4)时空联合因子分析与污染源解析结果表明:古城区内城河在时间段Ⅰ、Ⅱ、Ⅲ及古城区外城河和内外连接河道全年都受到生活污水及餐饮旅游等第三产业污水的污染,以及面临夏季藻类大量繁殖的风险.
5)绝对主成分多元线性回归(APCS-MLR)表明,总氮(TN)、氨氮(NH3-N)、总磷(TP)和高锰酸盐指数(CODMn)主要来自城市生活及餐饮旅游等第三产业污水.
5 建议(Suggestions)1)通过水质指数(WQI)模型分析结果可以看出,古城区内部河道水质相对较差,古城区外围河道水质较好,在后期具体开展工程措施治理河道水质方面,可以充分考虑采取引清调水,借助外来水源稀释古城区内河道水.
2)综合水质分析及源解析结果可知,苏州古城区水质时空特征明显,N、P污染严重,混杂居民生活污染源排放点多面广,对城中村居民生活污染应采取分散式分流截污设施,分步骤、分区域收集生活污水.
3)对于可能汇入河道的降雨径流污染应结合河道护岸带现状,河岸带种植既美观又可有效截留降雨地表径流的植被,有效堵截径流污染物入河.同时,城市规划及建设期间也可以因地制宜地采取最佳管理措施(BMPs),以及低影响开发措施(LID)等技术理念治理暴雨径流污染物进入河道.
4)对于河道内源污染底泥应在冬季进行河道生态清淤,消除内源污染物;对于河道水面漂浮垃圾,应多频次进行清捞;对于游客要加大宣传教育力度禁止丢弃垃圾,加强惩戒手段等.
致谢: 本研究在基础数据采集、分析、调研的过程中得到苏州市排水管理处的大力支持,在此表示感谢.
| [1] | Akbal F, Gurel L, Bahadir T, et al. 2011. Multivariate statistical techniques for the assessment of surface water quality at the Mid-Black Sea Coast of Turkey[J]. Water, Air, & Soil Pollution, 216 (1/4): 21-37 |
| [2] | Akkoyunlu A, Akiner M E. 2012. Pollution evaluation in streams using water quality indices: A case study from Turkey's Sapanca Lake Basin[J]. Ecological Indicators, 18: 501-511 |
| [3] | Bu H M, Tan X A, Li S Y, et al. 2010. Temporal and spatial variations of water quality in the Jinshui River of the South Qinling Mts., China[J]. Ecotoxicology and Environmental Safety, 73: 907-913 |
| [4] | 卜红梅, 刘文治, 张全发. 2009. 多元统计方法在金水河水质时空变化分析中的应用[J].资源科学, 31 (3): 429-434 |
| [5] | 曹阳,滕彦国,刘昀竺. 2013.宁夏吴忠市金积水源地地下水水质影响因素的多元统计分析[J].吉林大学学报(地球科学版), 43 (1): 235-244 |
| [6] | 陈彦光.2011.地理数学方法:基础和应用[M].北京:科学出版社.1-484 |
| [7] | Davis J C.1973.Statistics Date Analysis in Geology[M]. New York: Wiley. 1-656 |
| [8] | Espejo L, Kretschmer N, Oyarzun J, et al. 2012. Application of water quality indices and analysis of the surface water quality monitoring network in semiarid North-Central Chile[J]. Environmental Monitoring and Assessment, 184 (9): 5571-5588 |
| [9] | Guo H, Wang T, Louie P. 2004. Source apportionment of ambient non-methane hydrocarbons in Hong Kong: Application of a principal component analysis/absolute principal component scores (PCA/APCS) receptor model[J]. Environmental Pollution, 129 (3): 489-498 |
| [10] | 官剑颖. 2010. 苏州水资源可持续利用初探[J].水利建设与管理, (5):76-77 |
| [11] | Huang F, Wang X Q, Lou L P, et al. 2010. Spatial variation and source apportionment of water pollution in Qiantang River (China) using statistical techniques[J]. Water Research, 44 (5): 1562-1572 |
| [12] | 姜伟,黄明.2012. 苏州市城区河道黑臭成因分析及对策研究[J]. 中国水运(下半月), (10): 123-124 |
| [13] | Kowalkowski T, Szpejna J. 2006. Application of chemometrics in river water classification[J]. Water Research, 40 (4): 744-752 |
| [14] | Lattin J, Carroll D, Green P. 2003. Analyzing Multivariate Date[M]. New York: Duxbury. 1-200 |
| [15] | Lam Q D, Schmalz B, Fohrer N. 2012. Assessing the spatial and temporal variations of water quality in lowland areas, Northern Germany[J]. Journal of Hydrology, (438/439): 137-147 |
| [16] | 李文赞,李叙勇,王慧亮,等. 2012.滏阳河主要水环境污染物空间分布特性研究[J].环境科学学报,32 (11): 2814-2819 |
| [17] | Mei J L, Li Z C, Sun L H, et al. 2011. Assessment of heavy metals in the urban river sediments in Suzhou City, Northern Anhui Province, China[J]. Procedia Environmental Sciences, 10(Part C): 2547-2553 |
| [18] | Miller S L, Anderson M J, Daly E P, et al. 2002. Source apportionment of exposures to volatile organic compounds. I. Evaluation of receptor models using simulated exposure data[J]. Atmospheric Environment, 36(22): 3629-3641 |
| [19] | 祁赛君,王涌涛.2011.苏州城市典型汇水面雨水径流初期冲刷规律分析[J].环境科技,(S1): 41-43 |
| [20] | 瞿明凯,李卫东,张传荣,等.2013.基于受体模型和地统计学相结合的土壤镉污染源解析[J].中国环境科学, 33 (5): 854-860 |
| [21] | Shrestha S, Kazama F.2007.Assessment of surface water quality using multivariate statistical techniques: A case study of the Fuji river basin, Japan[J]. Environmental Modelling & Software, 22(4): 464-475 |
| [22] | Su S L, Zhi J J, Lou L P, et al. 2011. Spatio-temporal patterns and source apportionment of pollution in Qiantang River (China) using neural-based modeling and multivariate statistical techniques[J]. Physics and Chemistry of the Earth, Parts A/B/C, 36(9/11): 379-386 |
| [23] | Singh E,Gupta A,Singh N R.2013.Groundwater quality in Imphal West District, Manipur, India, with multivariate statistical analysis of data[J]. Environmental Science and Pollution Research, 20 (4): 2421-2434 |
| [24] | Singh K P, Sinha S. 2005. Water quality assessment and apportionment of pollution sources of Gomti River (India) using multivariate statistical techniques a case study[J]. Analytica Chimica Acta, 538 (1/2): 355-374 |
| [25] | Terrado M,Borrell E,de Campos S,et al.2010.Surface-water-quality indices for the analysis of data generated by automated sampling networks[J]. Trends in Analytical Chemistry, 29 (1): 40-52 |
| [26] | Wang X Z, Cai Q H, Ye L, et al.2012. Evaluation of spatial and temporal variation in stream water quality by multivariate statistical techniques: A case study of the Xiangxi River basin, China[J].Quaternary International, 282: 137-144 |
| [27] | Wang Y, Wang P, Bai Y J, et al. 2013. Assessment of surface water quality via multivariate statistical techniques: A case study of the Songhua River Harbin region, China[J]. Journal of Hydro-environment Research, 7 (1):30-40 |
| [28] | 王翠榆,杨永辉,周丰,等. 2012.沁河流域水体污染物时空分异特征及潜在污染源识别[J].环境科学学报, 32 (9): 2267-2278 |
| [29] | 王丽婧,汪星,刘录三,等. 2013.洞庭湖水质因子的多元分析[J].环境科学研究, 26 (1): 1-7 |
| [30] | 吴蓓,汪翙,黄玮,等. 2007.苏州城区不同功能区地表径流污染特征[J].水资源保护, 23 (2): 57-60 |
| [31] | 谢森,何连生,田学达,等.2010.巢湖水质时空分布模式研究[J].环境工程学报, 4 (3): 531-539 |
| [32] | 邢雅囡,阮晓红,赵振华.2006.城市河道底泥疏浚深度对氮磷释放的影响[J].河海大学学报(自然科学版), 34 (4): 378-382 |
| [33] | Xu H S,Xu Z X,Wu W,et al. 2012.Assessment and spatiotemporal variation analysis of water quality in the Zhangweinan River Basin, China[J]. Procedia Environmental Sciences, 13:1641-1652 |
| [34] | 严以新,蒋小欣,阮晓红, 等. 2008. 平原河网区城市水污染特征及控制对策研究[J].水资源保护, 24 (5): 1-4 |
| [35] | Yang Y H, Zhou F, Guo H C, et al. 2010. Analysis of spatial and temporal water pollution patterns in Lake Dianchi using multivariate statistical methods[J]. Environmental Monitoring and Assessment, 170 (1/4): 407- 416 |
| [36] | 张汪寿,李晓秀,王晓燕,等. 2012.北运河武清段水污染时空变异特征[J].环境科学学报, 32 (4): 836-846 |
| [37] | 赵鹏,夏北成,秦建桥,等. 2012.流域景观格局与河流水质的多变量相关分析[J].生态学报, 32 (8): 2331-2341 |
| [38] | Zhou F, Guo H C,Liu L.2007.Quantitative identification and source apportionment of anthropogenic heavy metals in marine sediment of Hong Kong[J]. Environmental Geology, 53 (2): 295-305 |
| [39] | 周丰,郝泽嘉,郭怀成. 2007.香港东部近海水质时空分布模式[J].环境科学学报, 27 (9): 1517-1524 |
 2014, Vol. 34
2014, Vol. 34


