随着流域内涵的不断演进,流域已经从单纯的水文集水单元概念发展到具有经济、社会和环境多种内涵的复合概念(周丰等,2007; 刘永等,2008),成为研究区域环境经济协调发展的重要尺度.流域环境经济协调发展研究在方法学上可以归纳为3大模型体系:评价模型、模拟模型和优化模型,其中模拟模型被用于构建经济社会发展与环境质量之间的输入输出关系,为评价和优化提供必要的数据支持和响应关系,是环境经济规划与预测研究中的核心方法之一.目前在流域环境经济协调发展中应用的模拟模型有系统动力学模型(袁绪英等,2012)、CGE模型(吴锋等,2010)、均衡分析模型(邓祥征等,2010)和回归模型(陈能汪等,2012)等,其中系统动力学模型在处理复杂、高阶、非线性问题时具有独特优势(钟永光与贾晓菁等,2009),并且可实现与其他模型的耦合,如灰色预测模型(张林波,2009)、水质模型(Kato,2005)、评价模型(郭长雷等,2006)、优化模型(Nasiri et al., 2013),是常用的流域系统模拟模型.
系统动力学方法的引入为流域经济、社会、环境的复杂反馈关系的模拟提供了新的方法与思路,在国内外各类流域环境经济优化决策中得到广泛的应用(Saysel et al., 2002; 方创琳等,2004; 李同升等,2006; 夏训峰等,2010; 王慧敏等,2001).然而,纵观目前系统动力学模型在流域环境经济优化决策中的案例,普遍存在缺乏反馈回路问题,即在系统流图中没有环状因果关系,某个变量的改变仅影响下游变量取值的变化,无法对自身行为形成反馈作用.这种缺乏反馈机制的系统动力学模型在系统行为的模拟上往往存在片面性,无法全面模拟变量之间复杂交互关系,给后续的优化决策带来了误差.如文献(夏训峰等,2010)建立了农业结构调整对氮磷排放量影响的系统动力学模型,畜禽饲养量作为农业结构的关键变量被设定为时间变量(以时间为因变量的函数,跟其它变量无关),仅构建了畜禽养殖数量变化对氮磷排放量的单向影响,缺失了氮磷排放量对畜禽养殖数量的逆向反馈作用.造成这种现象的原因可能来自2个方面:①流域系统的复杂性使得系统变量之间的反馈关系存在极大的不确定性.信息是环境决策基础(过孝民,1997),当决策者缺乏足够的信息时,制定的决策具有一定的随机性和不确定性,正如环境经济学中理性经济人的假设,当信息不足时,决策者的环境行为并不是理性的,因而也难以预测其变化方向.②变量之间的反馈强度具有强烈的非线性特征,难以量化表达.反馈强度是被作用变量对作用变量的影响能力,影响反馈强度的因素同样具有较大的不确定性,这种不确定性同样取决于决策者的信息掌握程度和价值评判标准.综合以上2点原因,可以认为获取关键系统信息和建立科学的价值评判体系可为构建流域系统复杂反馈关系提供一种途径.
为完善流域系统模拟模型中对复杂反馈关系的模拟,更好地为流域环境经济的优化提供决策支持.针对流域环境经济系统动力学模拟模型中变量反馈关系缺失的问题,本研究从系统优化的角度,基于综合评价模型(Assessment model)、系统动力学(System Dynamics,SD)模型和Powell优化模型,提出了流域“评价模拟优化”环境经济决策模型(简称ASO模型).通过模拟模型为决策者提供关键的决策支持信息,采用环境经济协调度模型建立支撑决策选择的价值评判体系,使用优化模型构建系统反馈回路的量化模型.最后,以抚仙湖流域为例,进行了案例研究.
2 流域环境经济决策优化模型(AssessmentSimulationOptimization coupled model) 2.1 模型框架流域环境经济决策优化模型由环境经济协调度模型、模拟模型和优化模型等3个子模型构成,其中环境经济协调度模型用于识别流域管理决策问题,同时建立基于规划目标的价值评判体系,确定决策的优化目标;以评价模型中涉及的指标为依据,基于“驱动力压力状态响应”关系构建流域系统各指标相互作用的模拟模型,确定决策变量与状态变量的“输入输出”响应关系,同时将评价模型耦合到模拟模型中;在评价模拟模型的基础上,以流域环境经济协调度最大化为目标,建立环境经济协调度指标对系统决策变量的反馈关系,完成输入输出输入的闭环反馈.
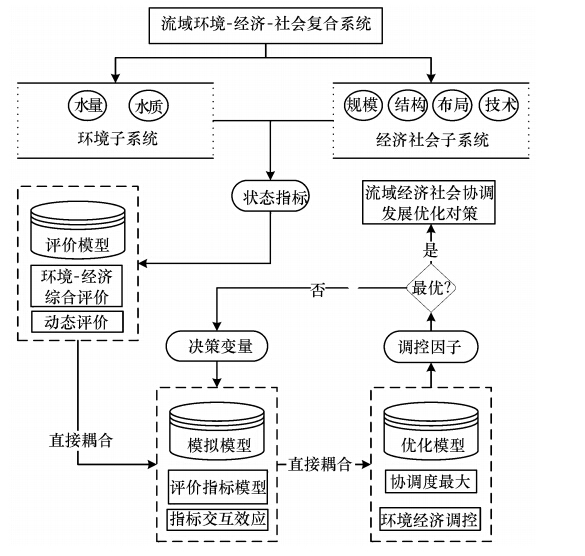 |
| 图 1 流域“评价模拟优化”耦合模型结构 Fig. 1 Structure of “AssessmentSimulationOptimization” coupled model |
流域环境经济协调发展涉及经济社会发展和水环境保护2个基本目标,其协调度评价从这两个目标的状态出发,分别评定流域经济发展水平和水环境保护水平以及它们的总体效应.根据评价模型的不同,可分为向量模法、算术加权法、几何加权法、因子分析法、人工神经网络法和投影寻踪法等(李川,2008; 高伟,2009; 高杨等,2010).不同评价模型的适用性存在差异,考虑计算方法的简洁性与评价结果的直观程度,选择加权法作为流域环境经济协调度评价模型.从结构上看,一个完整的评价模型应包括评价指标体系、指标标准化、指标权重、评价方法和评价标准等5个部分.
(1)评价指标体系.评价指标体系的构建应遵循完整性、典型性、简洁性等原则,从经济社会子系统和水环境子系统角度分别选取代表其发展质量的指标,建立多指标环境经济协调度模型.其中经济社会发展质量指标主要考虑经济社会的规模、结构、速率和平均水平;水环境质量指标则从水量、水质和水生态完整性角度选取指标.
(2)指标标准化.为消除指标量纲和性质不同对计算结果的影响,需要采用一定数据转换方法对其实行标准化,本研究选择极差法(式1)把各项指标处理为[0,1]之间的数值.经过指标值计算,所有的指标都具有无量纲化、越大越好、以1为基准的特点,便于指标的进一步计算和模型应用.
正向型指标(越大越好指标),
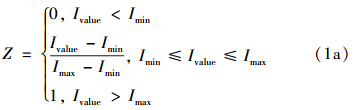
负向型指标(越小越好指标),
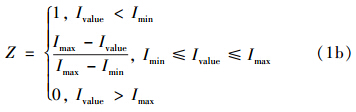
(3)指标权重计算.为体现不同指标取值变化对评价结果的影响,提出了一种新的指标权重计算法——变权法(式2);该法以等权法为基础,考虑指标与评价标准的偏离度的影响,偏离度越大,其权重越高,体现了极端变化指标对评价结果的重要影响.计算方法为:
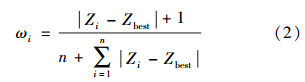
(4)流域环境经济协调度模型.经济社会与环境的协调发展是流域环境经济优化决策的基本目标,采用综合评价模型计算流域环境经济协调度,判断流域发展状态.基于变权法和算数加权平均法的思想,构建了流域环境经济协调度计算模型(公式3).
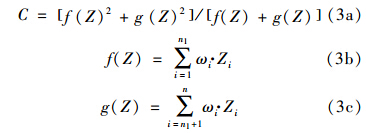
(5)评价标准确定.评价标准是判断指标优劣的依据,横向参照、纵向参照、科学实验、等分法等是确定评价标准的常用方法(徐鹏等,2013; 徐琳瑜等,2013; Halpern et al., 2012).具体方法的选择应综合考虑指标类型和数据可得性.对于环境质量类指标,为充分考虑环境本底的影响,建议纵向参照法,选择历史数据确定评价等级;对于经济社会数据应更多选用横向参照法,可采用区域截面数据确定标准.本研究根据流域社会、经济、水环境质量变化范围,将其划分为5个等级,等级划分的确定方法如下:基于区域数据、历史数据、环境标准得到指标序列,取其5%和95%(或极值)作为最劣和最优水平.
2.2.2 系统模拟模型从系统的角度看,流域是由经济、社会、水环境等多种要素构成的复杂系统,各要素之间存在密切的相互作用(刘永等,2008).流域内部的各要素的复杂交互作用具有典型的动态、高阶、反馈等特点.系统动力学(System Dynamics)在处理非线性、高阶次、复杂时变系统时具有独特的优势(钟永光等,2009),模型通过系统内部变量之间的反馈,模拟整个系统的行为变化与动态响应关系.因此,系统动力学方法适用于建立流域复杂系统的模拟模型.
系统反馈是系统动态学的核心概念.反馈是指X影响Y,反过来Y通过一系列因果链影响X,根据作用效应可分为正反馈和负反馈,其中负反馈使系统行为趋向平衡与稳定(钟永光等,2009).基于系统动力学思想,在研究流域系统环境经济协调发展时,应建立经济社会与水环境系统之间负反馈关系,使系统趋于均衡发展.从环境学角度看,经济社会发展是环境变化的主要驱动因素,因此经济社会与环境2个子系统构成了最主要的反馈对象,即经济社会发展引起水环境变化,水环境变化反过来对经济社会发展造成影响,这种反作用影响途径可以认为是流域的环境经济的决策,其因果关系可概化为图 2的形式.
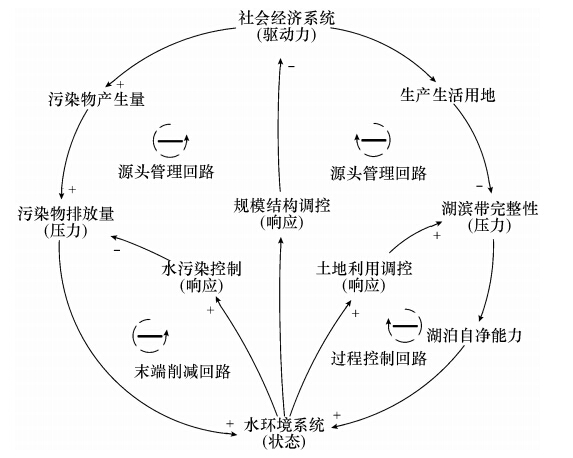 |
| 图 2 流域环境经济系统因果关系 Fig. 2 Casual loops of basin environmentsociety system |
系统动力学的基本变量类型有4种:状态变量、时间变量、辅助变量和常量.其中,状态变量是核心变量,用于模拟具有累积效应的变量,系统的高阶与非线性行为可通过不同状态变量的串联实现.系统动力学模型可以认为是显性的带有初始值的非线性微分方程的集合,其状态变量可用向量的形式表述(式(4)).
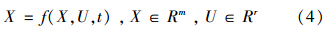
在ASO模型体系中,优化模型的作用是建立系统整体效用和系统控制变量之间的反馈关系,寻求最大系统效用下各控制变量的变化模式,从而为系统的最优决策提供支持.在本研究中,流域环境经济协调度是判断系统效用的综合评价指标,可作为优化目标,优化对象(控制变量)是经济社会规模、结构指标和水污染控制指标的调节系统.
(1)优化目标:流域环境经济协调度最大
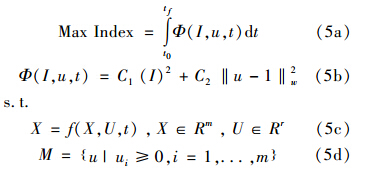
(2)决策变量:经济社会规模结构与环境治理水平的调节系数.
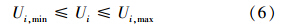
计算效率是模拟优化耦合模型中最主要的问题之一(盛虎等,2013),在选择优化模型时需要综合考虑算法的计算效率和有效性.目前与系统动力学模拟模型耦合的优化算法有遗传算法(Yu et al., 2012)、Powell算法(Nasiri et al., 2013)和单纯形法(Xu et al., 2012)等.在系统动力学软件Vensim DSS(DSS,Decision Support System)中,Powell优化算法被内嵌到Vensim计算平台中,实现了一个平台下的模拟优化直接耦合问题,为基于系统动力学的模拟优化的实现提供了便捷的方法.该优化模块是基于鲍威尔爬山算法(Powell hill climbing algorithm,简称Powell)(Powell,1964).Powell算法具有二次收敛性质的数值迭代方法,可进行复杂的多维函数曲面寻优,是解决动态优化问题常用的优化方法之一(Burns et al,2006).本研究基于Vensim DSS计算平台,实现SD模拟模型与Powell优化模型的直接耦合.
3 案例研究(Case study) 3.1 流域概况抚仙湖位于云南省玉溪市,位于北纬24°21′28″~ 24°38′00″,东经102°49′12″~102°57′26″之间.流域面积676.8 km2,跨澄江、江川、华宁3县,属珠江流域南盘江水系.湖泊面积212 km2,容水量185亿m3,理论换水周期长达167年,平均水深87.0 m,最大水深151.5 m(数据来源于:《云南省统计年鉴,2011》),是我国已知第二深水湖泊.抚仙湖流域多年平均径流量达到16218万m3,星云湖出流改道工程运行后的出水量2000万m3,抚仙湖可利用水资源量3743万m3.2010年末,抚仙湖流域内总人口为17.9万人,其中农业人口占88.5%.流域内国内生产总值达到50.74亿元(可变价),人均地区生产总值2.9万元,低于玉溪市平均水平(3.2万元).抚仙湖目前为贫营养型湖泊,水质清澈透明,含沙量很少,湖水中各生物营养元素的含量低,生物生产力较低,是我国为数不多的保持I类水质的大型淡水湖泊.
近年来,由于人类活动的干扰和自然环境变化,抚仙湖水质呈现恶化趋势,湖泊有机污染和营养化水平不断提高,高锰酸盐指数、TP和叶绿素a浓度有所上升,部分月份水质达到II类(荆春燕等,2004; 于洋等,2010; 王林等,2011)在流域经济社会发展目标的驱动下,抚仙湖水环境稳定达标面临巨大的压力,如何优化环境保护与经济社会发展的关系是实现流域环境经济协调发展的迫切需求.
3.2 抚仙湖ASO模型 3.2.1 数据来源本研究涉及的数据的主要来源是统计年鉴、环境统计数据、水资源公报、水环境公报、污染源普查数据、发表文献,以及地方不同部门的规划,或者实地调研.具体包括:云南省统计年鉴(2011);抚仙湖星云湖流域产业结构调整规划(2008—2027);抚仙湖生态安全调查与评估专题报告(2011);抚仙湖流域水污染防治“十二五”规划(2011);抚仙湖人工湿地及湖滨带工程效益研究报告(2011);抚仙湖流域全面保护与治理规划(2006—2020年);抚仙湖北岸沿湖村落污水收集与处理工程可行性研究报告(2011);抚仙湖东岸(华宁段)退田、退房还湖生态建设工程可行性研究报告(2008)及其他调研资料.
3.2.2 评价模型从经济社会发展和环境保护角度出发,选择反映其发展状态的相关指标,基于指标筛选的一般原则和数据可得性,共获得10项评价指标(表 1).其中经济社会发展水平类指标的筛选一般考虑人口数量、结构、变化率、生活水平和经济增长等因素,故选择了人口年均增长率、人口密度、城镇化率、人均GDP和GDP增长速度等5项指标;而环境质量类指标则从水质和水量两个目标的角度考虑,故选择4项常用水质指标和1项与水资源相关的指标.指标标准化和权重计算方法分别选用级差法和变权法(见2.2.1节).评价标准确定方法如下:经济社会发展类指标选择全国各31个省级行政区、282个地级市2010年数据(不包括台湾、香港、澳门地区;来源于《中国城市统计年鉴2011》和《中国统计年鉴2011年》)的5%、95%分位数作为最好或最差值,其对应标准值为0和1;环境类指标是选择抚仙湖1990—2011年水质最高值作为最差值(标准值=0),最低值作为最好值(标准值=1);其他指标如水资源开发利用率参考文献(王西琴等,2008).相应地,采用等分法抚仙湖流域环境经济协调度的等级划分为5个级别,以0.2为间距,分为优(0.8~1.0)、良(0.6~0.8)、中(0.4~0.6)、差(0.2~0.4)、劣(0~0.2).
| 表1 抚仙湖流域环境经济协调度评估指标体系 Table.1 Index system of comprehensive assessment for Lake Fuxianhu Basin |
抚仙湖流域系统是一个由经济、人口、水资源、水环境等构成的复合系统,面临的主要问题是经济和人口规模的扩张引发的产污量增加,进而导致湖体水量减少和水质恶化.基于Vensim DSS®(Ventana Simulation Environment Decision Support System)软件平台,构建了抚仙湖流域经济社会与环境系统的SD模拟模型.模型由207个变量构成,其中状态变量11个、辅助变量160个、常数36个,共包含3934个反馈回路.从类型和功能上看,该模型属于负反馈模型,重要的回路可以分为人口规模反馈回路、人口结构反馈回路、经济规模反馈回路、用水反馈回路和排污反馈回路,用来平衡经济社会发展与水环境之间的关系.
(1)模型边界:以抚仙湖流域边界为模型边界,涉及澄江、江川和华宁3县12个乡镇,面积1068 km2.基准年为2010年,规划年为2025年.
(2)参数率定:SD模型中的状态变量需要给出初始值,如初始年份(2010年)的城镇和农村人口数量,部分辅助变量(如表函数)需要建立数学函数关系,常数变量需要赋值,如产污系数、用水定额等.这些变量的赋值方法可以归纳为3种(秦耀辰等,1997):历史资料统计法、规划设定法和模型回归校正法.由于不同变量的性质不同,对不同变量采用的统计方法应有所区别.本研究主要依据历史资料统计法和规划设定法,即依据当地的统计数据和经济、社会、资源发展规划对模型参数赋值.
(3)模型结构:模型模拟了城镇生活、农村生活、地区生产总值、种植业、规模化畜禽养殖业、工业、水土流失、水资源和水环境等变量及其相互作用,以水量与水质(污染物)在各个要素间的驱动、过程和归宿为纽带建立反馈关系.
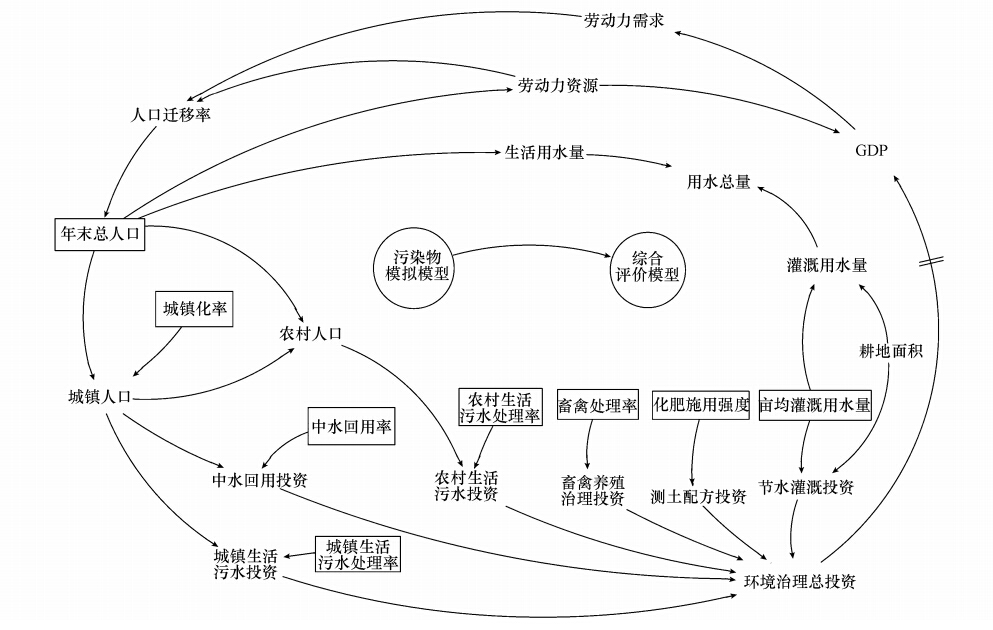 |
| 图 3 抚仙湖流域系统模拟SD简化流图(注:本研究的投资费用包括工程投资与运行费用2项,为简化流程,图中统一概化为投资费用) Fig. 3 Simplified system dynamic flow for Lake Fuxianhu Basin |
以流域环境经济协调度最大化为目标,通过优化主要调节回路的反馈强度指标(人口增长率、城镇化率、城镇污水处理率、农村生活污水处理率、中水回用率、化肥施用强度、亩均灌溉用水量),实现流域环境经济系统的优化决策.
3.2.5 模型检验SD模型的检验方法有参数敏感度检验、行为检验、历史检验等12方式(钟永光与贾晓菁等,2009).与一般统计学模型和物理模型不同,是否能够重现历史数据并不是SD模型关注的重点(钟永光等,2009),即SD的主要功能在于正确判别行为趋势而不是追求数据的精确性.故系统动力学更加关注模型的结构及其行为是否合理.其中,参数敏感性检验是测试系统结构是否稳定的常用方法.本研究基于Vensim DSS的Monte Carlo参数灵敏度测试功能,测试6项关键调控参数(中水回用率、化肥施用强度、农村生活污水处理率、城镇生活污水处理率、规模化畜禽养殖业粪便综合利用率、亩均灌溉用水量等)对流域环境经济协调度的灵敏度进行检验.模拟次数设置为200,数据采样方法选择拉丁超立方采样,参数分布使用随机均匀分布.当6项指标变化10%时,流域环境经济协调度的取值分布见图 4.由图可知,参数的变化对流域环境经济协调度的取值有一定的影响,特别是模拟初期2010—2014年,但由于调控参数的变化范围有限(如果污水处理率最高只能达到100%,不可能取到更高值),故模拟后期调控参数对模拟结果的影响非常有限.总体来说,调控参数取值的波动并未改变流域环境经济协调度变化的整体方向与趋势,即模型行为不受某些参数取值的控制,因此可以认为建立的模型在结构上是稳定的.
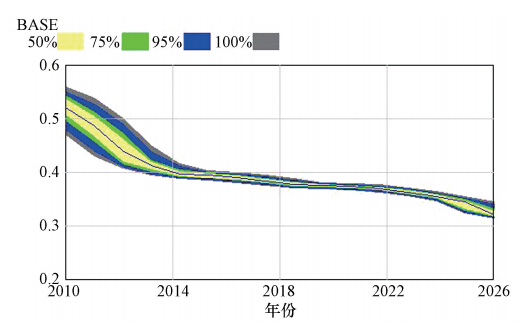 |
| 图 4 流域环境经济协调度的多参数灵敏度检验结果 Fig. 4 Multiparameter sensitivity of basin comprehensive assessment index |
基于3.1节的“评价模拟优化”模型,对抚仙湖流域2010—2025年经济社会发展与水环境变化进行模拟与优化,并与优化模式下(无反馈作用)的预测结果进行比较(图 5).结果F表明,2010现状年抚仙湖的流域环境经济协调度仅达到0.39,处于“差”评价等级(0.2~0.4).当前最主要的制约因素是经济社会的发展水平,其协调度仅达到0.30,水环境协调度略好,处于“中”等级水平,达到0.44,说明保证经济社会的持续发展与水环境的维持是流域未来规划的重要任务.
在非优化模式下(图 5中BASE),模拟结果显示在未来15年内,除经济社会发展评价度略有上升以外,抚仙湖流域的环境经济协调度和水环境协调度将出现下降趋势,尤其是水环境协调度将由现状的“中”等级下降到“差”等级,逼近“劣”等级.因此,延续现有发展方式将是不可取的,必须对流域的经济社会与水环境进行优化.
在优化模式下(图 5中OPT),以流域环境经济协调度最大化为目标,对经济社会发展规模、结构与环境措施节水减排措施进行了优化.与非优化模拟结果相比,流域环境经济协调度得到大幅提高,至2025年度由现状的0.39(差等级)提高到0.48(中等级),提高了47.2%;该模式下水环境恶化趋势不仅得到遏制,还能实现协调度的不断提高,至规划期末可达到0.57,提高了99.4%;但反馈模式对经济发展质量的改进能力有限,规划期内其协调度出现一定波动,但总体以上升趋势为主,规划期末较现状可提高11.0%,比反馈模式低3.3%.总体来看,非优化模式不能满足流域环境经济综合发展的需要,而优化模式可实现经济、社会、水环境的共赢.
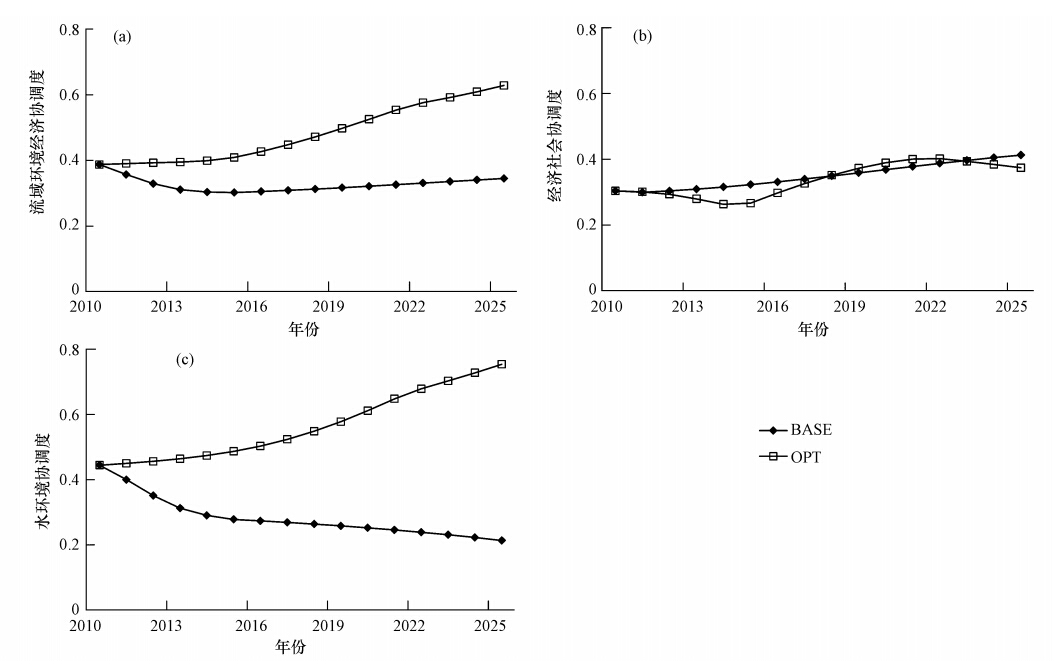 |
| 图 5 抚仙湖流域非优化模式(BASE)与优化模式(OPT)的评价度比较 Fig. 5 Comparison of assessment index between BASE and OPT modes in Lake Fuxianhu Basin |
在不同的发展模式,评价指标的取值存在较大的差异(图 6).从经济社会的评价指标看(图 6a~e),优化发展模式对经济发展强度和人口规模与结构提出了更严格的要求.相对于非优化模式下,地区经济发展速度必须有所控制,地区生产总值发展速度要逐年下调,到2025年不能超过5.6%(地区生产总值190.4亿元);人口增长速率到规划期末要控制在4.8‰以下(年末总人口19.3万人),同时促进人口结构向城镇化方向发展,加速城镇化步伐,到2025年达到88.3%.从水环境的评价指标看(图 6f~j),优化模式能实现水质的显著改善,同时对水量也有显著的控制作用.优化模式下,抚仙湖主要污染物的平均浓度能持续维持I类水质标准,规划期末高锰酸盐指数、TN浓度、TP浓度和Chla含量分别降至0.81、0.13、0.003 mg · L-1和1.36 mg · m-3,同时水资源开发利用率不会出现大幅提高,维持在75%以下,仅较非优化模式降低10个百分点.
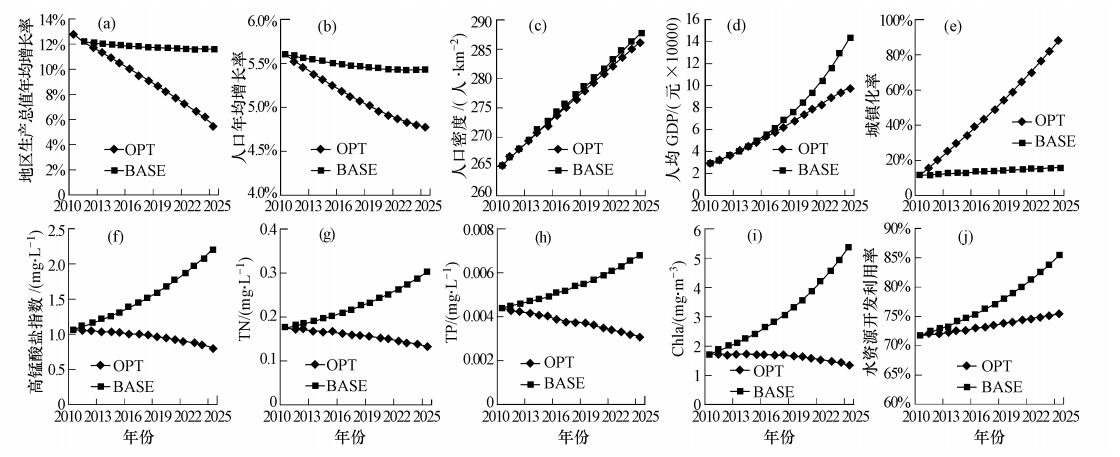 |
| 图 6 抚仙湖流域非优化模式(BASE)与优化模式(OPT)的评价指标比较 Fig. 6 Comparison of individual index between BASE and OPT modes in Lake Fuxianhu Basin |
反馈关系的量化表达是流域环境经济模拟过程中的重要技术难题.本研究基于综合评价模型、系统动力学仿真模型和Powell优化模型,构建了“评价模拟优化”流域综合决策模型(ASO模型),从系统优化的角度解决了流域模拟模型中反馈回路建立的难题,完善了复杂系统模拟与优化的理论与方法.该方法在抚仙湖流域的例证研究表明ASO模型能够有效的获得优于常规模拟方法的流域环境经济协调方案,并获得抚仙湖流域经济社会与水环境保护的发展优化值,为流域环境经济优化发展提供了决策支持.
流域系统优化是一个复杂的系统工程,亟需管理理念、模型方法、环境政策等多方面的创新以及多学科之间的交叉和互补研究.本研究仅从方法学角度对基于SD模型和Powell优化模型的流域系统管理技术实现进行了尝试,在流域环境与经济相互作用的方式、途径、效应等方面的分析还存在许多不足.未来流域环境经济系统优化与SD模型的应用应重点关注和解决至少3个方面的问题:①完善流域发展多目标之间的博弈与均衡理论与方法,不同发展目标之间具有复杂的响应关系,往往难以实现所有目标的最大化,在优化决策时必须兼顾各种目标的均衡,寻找发展的适宜空间;②集成SD模型与统计模型、物理模型,经济社会发展问题与环境问题十分复杂,不可能也不必要完全由SD模型完成,应尽可能的结合其他专业模型或统计模型实现对非关键过程的简化;③发展SD模型的空间布局优化功能,SD模型具有较强的时间变化问题处理能力,但在空间模拟上存在明显不足,如何将SD的时间序列模拟功能与其他空间模拟模型有效结合起来也是未来系统动力学与流域综合管理相结合可尝试的研究方向.
| [1] | Burns J R, Janamanchi B.2006.Optimal control and optimization of system dynamics models: some experiences and recommendations[A].Proceedings of 24th International Conference of the System Dynamics Society.Nijmegen, the Netherlands |
| [2] | 陈能汪, 王龙剑, 林辉, 等.2012.九龙江流域经济发展与河流水质时空关联分析[J].生态与农村环境学报, 28(1): 19-25 |
| [3] | 邓祥征, 吴锋, 席北斗, 等.2010.鄱阳湖流域经济发展与氮、磷减排调控关系的均衡分析[J].中国环境科学, 30(增刊): 92-96 |
| [4] | 方创琳, 鲍超.2004.黑河流域水-生态-经济发展耦合模型及应用[J].地理学报, 59(5): 781-790 |
| [5] | 高伟.2009.湖州市水环境承载力评价[J].水利科技与经济, 15(11): 947-949 |
| [6] | 高杨, 黄华梅, 吴志峰.2010.基于投影寻踪的珠江三角洲景观生态安全评价[J].生态学报, 30(21): 5894-5903 |
| [7] | 郭长雷, 王丽婧, 梅凤乔, 等.2006.贵阳市环境经济系统协调发展策略分析[J].长江流域资源与环境, 15(4): 427-433 |
| [8] | 过孝民.1997.环境决策与信息支持[J].环境科学研究, 10(5): 5-8 |
| [9] | Halpern B S, Longo C, Hardy D, et al.2012.An index to assess the health and benefits of the global ocean[J].Nature, 488(7413): 615-620 |
| [10] | 荆春燕, 张秀敏, 赵祥华.2004.抚仙湖水质变化趋势分析[J].云南环境科学, 23(增刊): 110-111, 114 |
| [11] | Kato T.2005.Simulation of water quality with the application of system dynamics model for population and land-use changes[J].Paddy and Water Environment, 3(2): 103-109 |
| [12] | 李川.2008.水环境承载力量化方法的研究进展[J].环境科学与管理, 33(8): 66-69, 111 |
| [13] | 李同升, 徐冬平.2006.基于SD模型下的流域水资源-社会经济系统时空协同分析——以渭河流域关中段为例[J].地理科学, 26(5): 551-556 |
| [14] | 刘永, 郭怀成.2008.湖泊-流域生态系统管理研究[M].北京: 科学出版社 |
| [15] | Nasiri F, Savage T, Wang R, et al.2013.A system dynamics approach for urban water reuse planning: a case study from the Great Lakes region[J].Stochastic Environmental Research and Risk Assessment, 27(3): 675-691 |
| [16] | Powell M.1964.Efficient method for finding minimum of function of several-variables without calculating derivatives[J].Computer Journal, 7(2): 155-162 |
| [17] | 秦耀辰, 赵秉栋, 赵俊军, 等.1997.河南省持续发展系统动力学模拟与调控[J].系统工程理论与实践, (7): 126-133 |
| [18] | Saysel A K, Barlas Y, Yenigüm O, et al.2002.Environmental sustainability in an agricultural development project: a system dynamics approach[J].Journal of Environmental Management, 64(3): 247-260 |
| [19] | 盛虎, 向男, 郭怀成, 等.2013.流域水质管理优化决策模型研究[J].环境科学学报, 33(1): 1-8 |
| [20] | 王慧敏, 刘新仁, 徐立中.2001.流域可持续发展的系统动力学预警方法研究[J].系统工程, 19(3): 61-68 |
| [21] | 王林, 刘宇, 祁云宽, 等.2011.抚仙湖流域社会经济发展与环境压力分析[J].环境科学导刊, 30(5): 30-32 |
| [22] | 王西琴, 张远.2008.中国七大河流水资源开发利用率阈值[J].自然资源学报, 23(3): 500-506 |
| [23] | 吴锋, 邓祥征, 林英志.2010.基于环境CGE模型的鄱阳湖流域氮磷排放调控方案及影响模拟[J].地球信息科学学报, 12(1): 26-33 |
| [24] | 夏训峰, 顾雨, 席北斗, 等.2010.基于水环境约束的抚仙湖流域农业结构调整研究[J].环境科学研究, 23(10): 1274-1278 |
| [25] | Xu J P, Yang J, Yao, L M, et al.2012.Transportation structure analysis using SD-MOP in world modern garden city: a case study in China[J].Discrete Dynamics in Nature and Society, (710854), Doi:10.1155/2012/710854 |
| [26] | 徐琳瑜, 康鹏.2013.工业园区规划环境影响评价中的环境承载力方法研究[J].环境科学学报, 33(3): 918-930 |
| [27] | 徐鹏, 高伟, 周丰, 等.2013.流域社会经济的水环境效应评估新方法及在南四湖的应用[J].环境科学学报, 33(8): 2285-2295 |
| [28] | Yu S W, Wei Y M.2012.Prediction of China's coal production-environmental pollution based on a hybrid genetic algorithm-system dynamics model[J].Energy Policy, 42: 521-529 |
| [29] | 于洋, 张民, 钱善勤, 等.2010.云贵高原湖泊水质现状及演变[J].湖泊科学, 22(6): 820-828 |
| [30] | 袁绪英, 吴宜进, 李星明.2012.流域系统动力学模型的全耦合问题研究进展[J].环境科学与管理, 37(4): 68-72 |
| [31] | 张林波.2009.城市生态承载力理论与方法研究 以深圳为例[M].北京: 中国环境科学出版社 |
| [32] | 钟永光, 贾晓菁, 李旭, 等.2009.系统动力学[M].北京: 科学出版社 |
| [33] | 周丰, 刘永, 黄凯, 等.2007.流域水环境功能区划及其关键问题[J].水科学进展, 18(2): 216-222 |
 2014, Vol. 34
2014, Vol. 34


