絮凝是混凝水处理过程中的重要阶段之一.絮凝过程中，絮体粒径分布及形态学特征时刻变化，其群体形貌动态变化过程复杂.近年来，许多学者采用分形数学理论来描述絮体在不同工况条件下的颗粒几何特征，以期通过定量描述絮体形貌的复杂性，揭示絮体形成及其与工艺效能的内在关系.

众所周知，凝聚是一个颗粒随机碰撞的过程，具有非线性特征.分形维数常用来描述具有自相似结构的不规则几何体的非线性工作机理.在絮凝过程中，絮体颗粒形态和粒径分布时刻变化，而简单分形维数主要用于描述和表征颗粒群体的整体性和平均性，不能完全揭示絮体分形变化的动力学过程(张德祥等，2007;Brown et al., 1992).多重分形描述不同局部条件或不同层次所导致的特殊结构行为与特征，从系统的局部出发来研究整体的特征，并借助统计物理学的方法讨论特征参量概率测度的分布规律.目前多重分形理论已广泛应用于土壤环境(Grout et al., 1998;Li et al., 2011)、材料(Pérez et al., 2012)、地球科学(García-Marín et al., 2008)、医学(Song et al., 2013;Vasiljevic et al., 2012)、城市规划(Ariza-Villaverde et al., 2013)等诸多领域，在国内外水处理领域中未见相关研究内容.实际检测操作中对特定絮体的生长过程监测存在困难，但絮体的群体生长在一定范围内存在统计学自相似特征和标度不变性，可以用多重分形理论研究并定量描述絮体的生长规律.

絮体形态和分布特征的定量化对絮凝机理的完善和工艺控制均有重要的理论价值.本研究在前人基础上采用多重分形理论定量描述絮体群在生长过程中的分布特征，探讨絮体在生长过程中的多重分形行为.

1977年，M and elbrot将分形集的概念引入并对分形的定义进行了阐述.分形维数区别于欧式几何中对象的拓扑维数，它是描述非线性复杂系统特征的工具.分形几何学广泛应用于图形图像的分析处理，对于不规则形状物体的二维数字图像，应用计算机程序可以非常方便的计算物体的分形维数.计算分形维数的方法有很多，有盒计维数、相似维数、容量维数、关联维数、信息维数、面积周长维数等.盒计维数是在计算机图形图像处理中应用最广泛的分形维数算法之一，其基本的算法原理是以不同测度的盒子来测量目标数目，最后得到一个形如下式的幂函数关系：

多重分形是在简单分形基础上发展的分形理论，自1980年即已成为不规则物体形态分析的基本工具(Ficker，2004).多重分形谱由两种关系组成，一种是由一系列概率P_i，ε所组成的子集与测度之间的幂函数关系：P_i，ε∝ε^α，α称为奇异指数，其反映的是分形图像中概率集合随测度的变化关系，即反映了分形对象的奇异程度；另一种是一系列测度下的盒子数N(ε)与测度之间的幂函数关系：N(ε)∝ε^f(α).此处f(α)即为多重分形谱，显然它表示的是同一α值子集的分形维数.

多重分形谱的计算处理过程，首先需定义配分函数，此函数是对概率的加权求和，即：

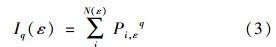
对于二维图像的多重分析，概率P_i，ε为盒子中研究目标所占的像素数量与图像中研究目标所占的总像素数量比：

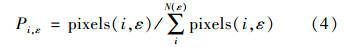
配分函数与尺度ε存在幂函数关系I_q(ε)= ετ(q)，两边取对数，则可得到

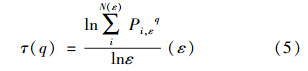
此处τ(q)称为质量指数，其反映的是I_q(ε)与lnε的线性关系，这种关系指定分形的无标度性.

广义分形维数D_q随q值的不同而具有不同的意义，其定义式如下：

当q=0，此时I₀反应二维图像中对象的空间几何性质，与概率P无关，这样D₀就表示普通的豪斯道夫维数，此时对应于f(α)_max(谢淑云等，2009).

根据τ(q)和q的关系经统计物理学中的勒让德变换后得到：

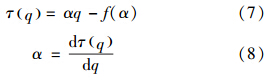
由此可得到，α-f(α)的关系，即多重分形图谱.根据多重分形理论，多重分形谱携带大量研究对象的定量信息，f(α_max)、α_max反映的是概率最小子集的性质；f(α_min)、α_min反映的是概率最大子集的性质，f(α)_max和其对应的α₀反映的是最或然子集的性质；多重分形谱谱宽Δα=α_max-α_min反映了概率分布范围的大小，概率分布愈不均匀，相应的谱宽会越大；Δf(α)=f(α_max)- f(α_min)反映的是最大、最小概率单元数目之间的比例关系(Ficker，2004).

原水为人工配制高岭土浑浊液，浊度(100±3)NTU.混凝剂为聚合硫酸铁(PFS，投加浓度30 mg · L^-1).试验设备为一套混凝图像在线监测系统，主体反应槽是容积为15 L的有机玻璃制圆形反应罐，IKA在线程序可控搅拌器，Prosical相机(相机设置像素512×512，像素大小7.4 μm ×7.4 μm，最小快门速度20 μs)实时捕捉图像，理论识别能力50 μm.

装置示意图如图 1所示，整个反应过程在反应槽内进行，少量反应悬浊液在蠕动泵的工作下以一定流速通过侧向打开的图像采集通道，图像采集通道尺寸为3 mm×50 mm×200 mm；打开光源控制器，将相机对焦以看清通道内絮体，相机采集流经通道的悬浮颗粒图像并将图像保存在计算机上待软件分析.

图 1(Fig. 1)

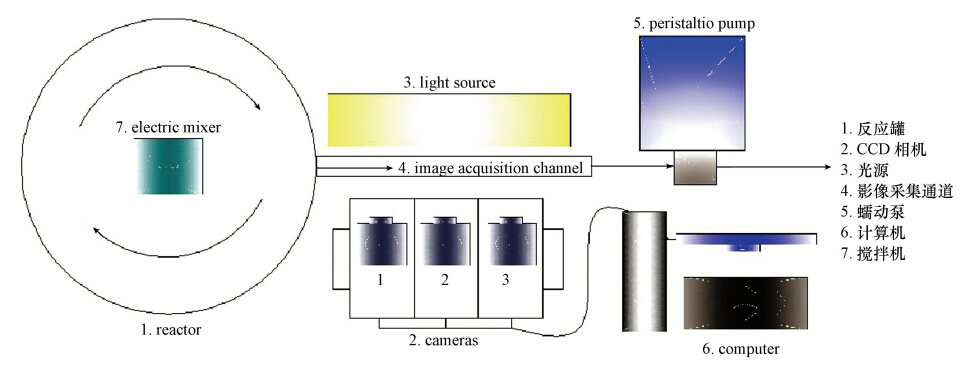图 1 混凝图像在线监测系统示意图 Fig. 1 Schematic of coagulation image on-line monitoring system

反应槽内进行混凝剂聚合硫酸铁处理模拟地表水试验，反应共历时770 s.将配制好的聚合铁混凝剂投入水中，在转速200 r · min^-1的条件下快速搅拌50 s；然后慢速搅拌720 s，转速75 r · min^-1.悬浊液以10 mm · s^-1的流速流经图像采集通道，相机每10 s采集1次图像并保存于计算机中，视窗大小2.19 cm×2.19 cm.

图像处理：该文所采用图像处理软件为Image-Pro Plus，相机采集到的图像格式为256灰度图，通过软件进行阈值转换法二值化处理后，计算图像上的颗粒数目、平均粒径(等效投影面积直径)，并计算图像的多重分形谱.

多重分形谱计算程序的参数设置：加权系数q取10，盒子大小取8、12、16、32、64、128、256、512.

混凝剂在快速搅拌条件下迅速分散到水中，此阶段混凝剂与水充分混合并水解，使水中悬浮颗粒脱稳，进入慢速搅拌阶段，脱稳颗粒开始凝聚，即絮体开始生长.

如图 2所示，反应体系经过快速搅拌段进入慢速搅拌段后，絮体颗粒数目迅速下降，由最初视野范围内的8000左右降至700左右，颗粒团聚现象明显；同时絮体颗粒的平均粒径大小迅速上升，由平均粒径0.09 mm左右迅速升至0.23 mm左右.从时 间分布上看，絮体生长阶段在整个反应过程中所占比例不大，絮体生长速度快.

图 2(Fig. 2)

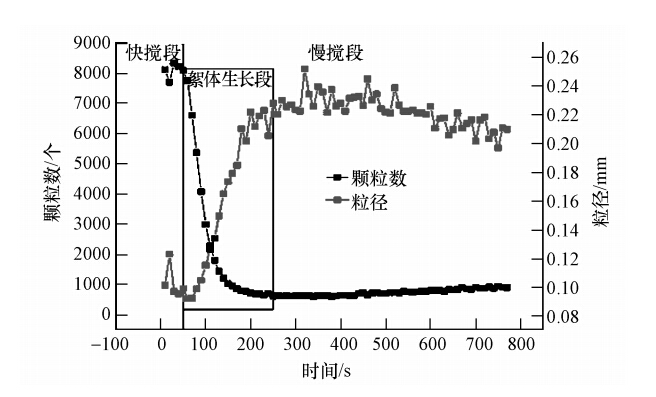图 2 絮体生长过程 Fig. 2 Flocs growth process

图 3显示的是絮体在生长过程中几个时间点分布情况.从图中可以看出，进入絮凝阶段后，小粒径颗粒迅速降低，大颗粒数目则明显增多，分布图形由高峰逐渐向低峰发展；同时，由于颗粒之间的团聚，颗粒粒径范围逐渐增大，即峰宽逐渐变大.在此需要说明的是，受到相机分辨率以及镜头分辨率等因素影响，小颗粒在图片中的识别能力有限.

图 3(Fig. 3)

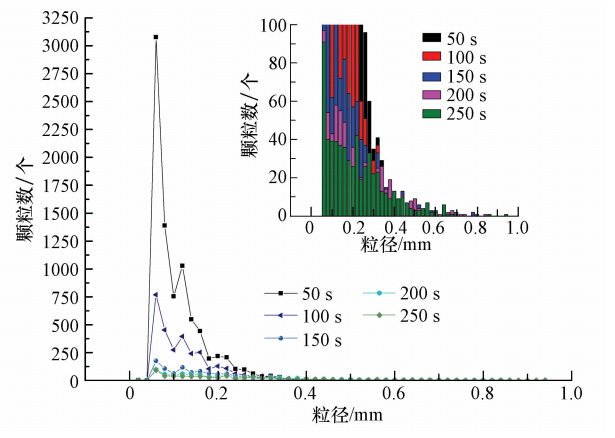图 3 絮体分布变化过程 Fig. 3 Flocs distribution change

图 4是相应的各取样时间点絮体生长的多重分形谱变化情况.从此图可以很直观的看出多重分形谱在整个絮体生长段的变化，f(α)_max逐渐降低，谱宽逐渐变大，絮体的多重分形谱从左勾状曲线逐渐变化为右钩状曲线.

图 4(Fig. 4)

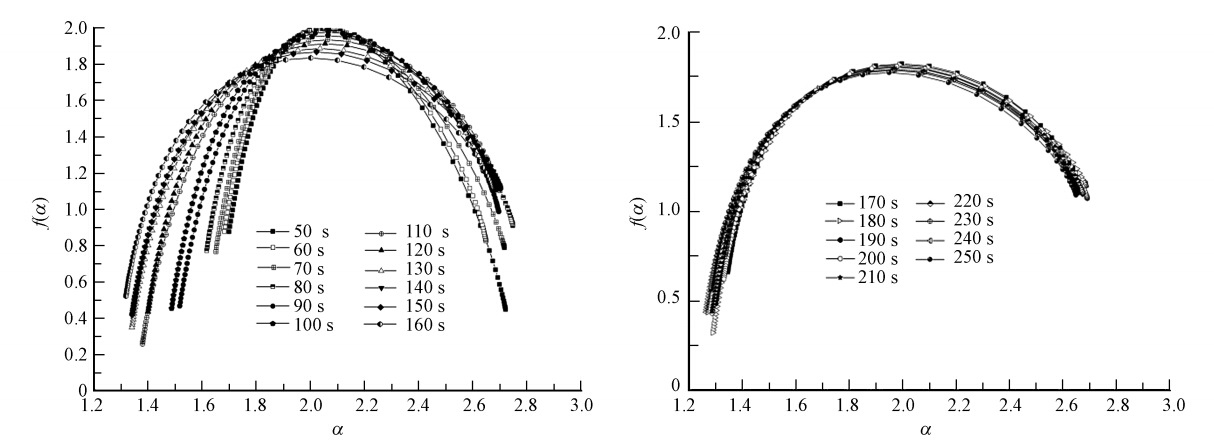图 4 絮体生长的多重分形谱 Fig. 4 Multifractal spectrum of flocs growth

图 5的部分数据显示出了多重分形谱中f(α_max)、α_max、f(α_min)、α_min、Δf(α)、Δα等特征参数随絮体生长的变化，表 1显示的是絮体群生长过程中部分采集点照片的多重分形谱参数数据.可以看出，f(α_max)在50~130 s范围内上升明显，由0.4469上升为1.2097，140 s后表现稳定；f(α_min)在絮体生长前段由0.8768下降到0.2568，后端亦是在一定幅度内波动.这说明小概率对象即大粒径絮体的数量在增加，大概率对象即小粒径絮体的数量在减小.由Δf(α)= f(α_max)-f(α_min)的变化可知，Δf(α)由最初的-0.4299迅速增大到0.8679，随后始终维持在一个较高水平.在70 s之前，Δf(α)<0，此时在整个体系中以小粒径颗粒在颗粒分布占据主导地位；此后Δf(α)转而大于0，并持续上升，说明大粒径颗粒所表示的小概率颗粒在颗粒分布中逐渐抢占主导地位；130 s后Δf(α)表现相对稳定，说明大概率和小概率颗粒的数目比相对稳定.图 3中表现出的分布情况也显示出150 s、200 s和250 s之间的波峰和波谷比例已相对稳定.

图 5(Fig. 5)

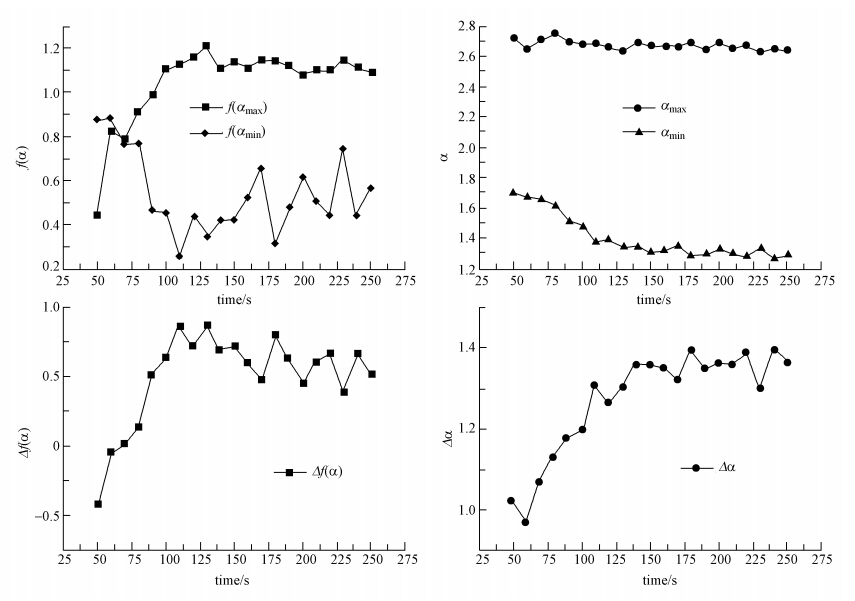图 5 絮体生长f(αmax)、αmax、f(αmin)、αmin、Δf(α)、Δα变化 Fig. 5 f(αmax)，αmax，f(αmin)，αmin，Δf(α) and Δα change of flocs growth

在整个反应进程中，α_max表现出相对平稳特征，这是由于α_max表示小概率颗粒，体现了最大粒径颗粒在絮体分布中所占比例始终保持平稳；而大概率颗粒所代表的α_min呈现出明显下降趋势，由1.7降至1.3左右，体现了小颗粒在絮体生长段的聚集过程.Δα在整个生长段则表现出稳步上升的趋势，由1.0213至1.3659.根据多重分形理论，Δα=α_max-α_min反映了概率分布范围的大小，概率分布愈不均匀，相应的谱宽会越大；也就是说，Δα在絮体生长的过程中的增大，说明絮体粒径范围在扩大，概率分布变得越来越不均匀.从图 3中也注意到絮体分布的峰宽逐渐增加.

图 6所示的是在多重分形谱中f(α)_max、α₀在絮体生长进程中的行进趋势.根据多重分形理论的性质，当q=0时，D₀为简单维数，此时对应于f(α) _max，与α₀一起反映了最或然子集的性质，即反映了絮体群的整体几何特征.结合表 1的数据，由于絮体在生长初期会经过碰撞简单的结合在一起，α₀在最初的30s内处于上升状态，从2.0474升至2.0658，这说明絮体群整体的奇异程度在上升；而后处于持续下降的过程，至絮体生长段末α₀降至1.9501，这是因为絮体颗粒数目迅速减少并且絮体开始团聚并相互挤压，使絮体群的整体奇异性下降，并且由于颗粒数目的降低和絮体群空间占有率下降，f(α)_max伴随絮体的生长而呈下降态势，由1.9995降至1.7762.

图 6(Fig. 6)

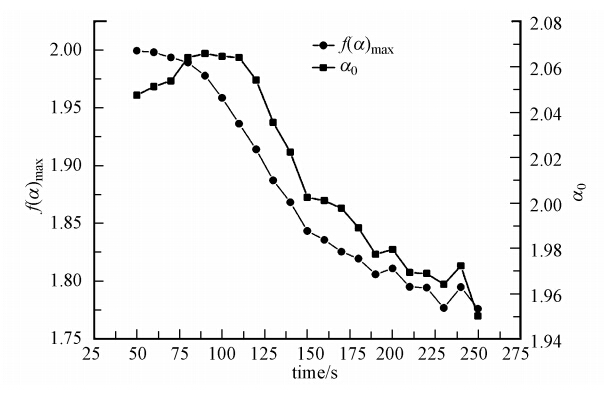图 6 絮体生长f(α) max、α0变化 Fig. 6 f(α) max and α0 change of flocs growth

表1(Table.1)

表1 部分絮体照片的多重分形谱参数 Table.1 Multifractal spectrum parameters of part of floc images

表1 部分絮体照片的多重分形谱参数 Table.1 Multifractal spectrum parameters of part of floc images 时间/s 参数 f(αmax) f(αmin) Δf(α) αmin αmax Δα f(α)max α0 50 0.4469 0.8768 -0.4299 1.7000 2.7213 1.0213 1.9995 2.0474 70 0.7878 0.7666 0.0212 1.6511 2.7172 1.0661 1.9936 2.0537 90 0.9871 0.4673 0.5198 1.5177 2.6956 1.1779 1.9778 2.0658 110 1.1247 0.2568 0.8679 1.3796 2.6888 1.3092 1.9363 2.0640 130 1.2097 0.3479 0.8618 1.3409 2.6421 1.3012 1.8873 2.0354 150 1.1376 0.4180 0.7196 1.3093 2.6672 1.3579 1.8435 2.0024 170 1.1453 0.6614 0.4839 1.3467 2.6665 1.3198 1.8255 1.9976 190 1.1172 0.4836 0.6336 1.3013 2.6504 1.3491 1.8060 1.9774 210 1.1019 0.5020 0.5999 1.2967 2.6552 1.3585 1.7951 1.9693 230 1.1457 0.7487 0.3970 1.3358 2.6361 1.3003 1.7768 1.9641 250 1.0924 0.5666 0.5258 1.2838 2.6497 1.3659 1.7762 1.9501

结合图 2，发现絮体生长段的多重分形特征参数变化并非随平均粒径的持续增大和颗粒数的持续减小而呈现持续的变化特性，如图 5中f(α_max)、f(α_min)、α_min、Δf(α)、Δα在110~130 s之前变化显著，而后出现上下波动或变化变缓的现象，图 6中α₀则出现先上升后下降的现象.这些不单单是由于絮体几何形态发生变化，也与絮体分布特征的变化密切相关.如图 3中所显示的情况，絮体在150 s后的分布变化较之150 s之前的变化已经非常小，150 s之前，絮体主要以小颗粒碰撞聚集为主，表现为f(α_max)、f(α_min)、α_min、Δf(α)、Δα等参数的迅速变化；150 s之后絮体团族之间的聚集增多，较大粒径颗粒出现，小颗粒进一步减少，这时的絮体概率分布不会出现太大的变化，但会向右缓慢发展.

通过对在絮凝生长过程中连续采集的絮体图片的分析研究发现，多重分形谱及其特征参数可以定量描述絮体在成长过程中的絮体形态和分布的动态变化情况，从而获取更多的絮体成长信息.当小颗粒进入到絮凝阶段，多重分形谱图由左勾状转变为右钩状，体现了絮体由小颗粒聚集为大颗粒的变化过程.Δα逐渐增大，表现出絮体分布的不均匀程度变化过程；Δf(α)的数值由负转正的变化指示了絮体群落中絮体的主导地位变化；简单分形维数f(α)_max则逐渐下降.

絮体形态和分布特征的变化是絮凝过程中的重要现象，对其定量化有助于促进絮凝动力学研究及絮凝机理的完善.结合絮凝剂的反应机理和流体在不同条件下的紊动耗散规律，多重分形分析可揭示絮体的动态絮凝行为特征，为絮凝的过程控制提供重要的参考数据，更多相关内容正在进一步研究中.