现代石油钻探和生产工作需要大量相关的井下参数信息，这些信息主要包括井眼参数、地层孔隙度、体积密度等。使用中子源测量地层孔隙度已经很多年了。中子从中子源（如Am-Be、D-T中子源）中发射出来后，穿过地层被减速后，常以超热中子和热中子的形式被探测。探测器中子计数率大小随中子在地层中的穿透能力（减速长度）而变化，而穿透能力主要受地层孔隙中氢原子含量的制约。这主要是因为：1)中子测井的基本原理是基于快中子最有效的减速原子是氢原子，因为其原子量与中子的相近；2)地层中的大多数氢原子以液体状态（水或者碳氢化合物）存在于地层的孔隙中。

在过去的几十年里，Am-Be中子源是最常用的用来测量地层孔隙度的中子源^[1-3]。但由于Am-Be中子源储存、运输、装卸操作、环境安全与回收等问题，同时为了适应新的测井需要，D-T中子源逐渐开始取代Am-Be中子源来测量地层中子孔隙度^[4-8]。相对Am-Be中子源发射平均能量为4.5MeV快中子，D-T中子源发射的单能快中子能量更高，为14MeV。这将导致两者地层孔隙度灵敏度有显著区别，同一孔隙度下中子初始能量越高，灵敏度越低。随孔隙度的增加，同一个中子源的孔隙度灵敏度也迅速降低^[9-13]。

1994年，Scott、Wraight等^{[5, 14]}通过将近探测器设置在对地层密度不敏感的源距处，测量得到的视孔隙度与地层含氢指数很接近，从仪器结构设计上降低了地层密度效应。2005年，斯伦贝谢(Schlumberger)公司^[7]介绍使用D-T中子源随钻仪器测量地层孔隙度，提出了一种将近、远计数率比值经过密度校正后，求取地层的含氢指数方法，但没有具体描述。随后2006年，Ellis等^[15-16]认为近、远探测器计数率响应与地层体积密度和含氢指数相关，并给出了计数率与含氢指数和体积密度的正比关系公式，通过对计数率进行体积密度校正，可以得到与地层体积密度无关的地层含氢指数。2016年，Liu等^[17]将影响计数率比值的含氢指数和体积密度两个因素影响使用蒙特卡罗数值分别模拟研究，得到一个与地层体积密度无关的含氢指数值。

为了研究和对比不同地层对脉冲中子孔隙度测量结果的影响。本文基于粒子输运程序MCNP (Monte Carlo N Particle Transport Code)^[18]和SNUPAR (Schlumberger’s Nuclear Parameter Code)^[19]及快中子与地层中原子核碰撞的物理原理，计算分析并推导中子孔隙度仪器的超热中子计数率比值（中子减速长度）响应与地层体积密度及含氢指数之间的关系。通过对近、远探测器的计数率比值进行体积密度校正，可以很好地降低地层体积密度影响，提高仪器对地层孔隙度的灵敏度，同时可以显著降低岩性和泥岩的影响。

脉冲中子孔隙度的计算机模拟是基于蒙特卡罗模型开发的MCNP程序。蒙特卡罗方法是在三维模型中，通过随机取样模拟中子、光子和电子输运过程。该程序需要详细地对仪器进行材料和几何描述。

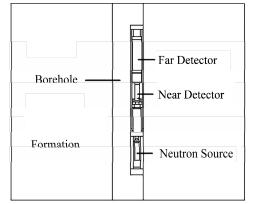
计算模型如图 1所示。模型为圆筒状、高150cm、直径150cm、井眼直径20cm的裸眼井。其主要由地层、仪器、井眼等组成。仪器包括一个脉冲中子源和两个不同尺寸的³He超热中子探测器组成。其中短探测器尺寸为∅28 mm×120mm，灵敏区长度为101mm，内充1.9×10⁵Pa的³He气体。长探测器尺寸为∅56mm×237mm，灵敏区长度为203mm，内充5×10⁵Pa的³He气体。仪器贴井壁偏心测量。井眼内为淡水，密度为1.0g·cm^-3。使用Fm计数乘子卡，考虑³He气体与中子的反应截面，使模拟的结果更能真实反映仪器的响应，并用F4栅元计数方式。

图 1

图 1 脉冲中子孔隙度测井模型 Figure 1 Pulsed source neutron porosity logging model

探测器中子计数率比值大小随中子在地层中的穿透能力（减速长度）而变化，而穿透能力主要受地层孔隙中氢原子含量的制约。在标准条件下，中子孔隙度仪器是被设计用来测量地层孔隙度的。即使对井眼尺寸、泥浆比重、泥浆矿化度、间隙、温度、压力和地层矿化度等进行环境校正后，仍然存在许多因素影响仪器的响应，例如岩性改变、泥岩存在等因素。由于脉冲发射的中子能量较高，与化学中子源比较，地层的非弹性散射影响不可忽略，因此，在脉冲中子孔隙度测井中岩性或地层密度对含氢指数测量的影响增强，并导致测量地层孔隙度灵敏度降低。

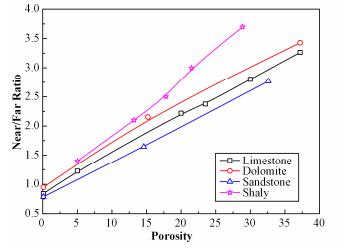
图 2为不同岩性及泥岩地层近、远计数率比值与地层孔隙度的关系。传统的比值-孔隙度关系转换是在灰岩地层中进行的。从图 2中可以看到，对于同一孔隙度地层，对应不同岩性及泥岩地层的近、远计数率比值也不一样，其中含泥岩地层最大、白云岩其次、砂岩最小。说明地层岩性和泥岩对地层中子孔隙度测量影响很大。

图 2

图 2 近、远探测器计数率比值与地层孔隙度关系 Figure 2 Relationship between the ratio of count rate of near and far detectors and formation porosity

对于中子源发射的快中子，在地层中的减速过程主要通过与地层中原子核发生非弹性散射和弹性散射来完成，可通过减速长度L_s来描述。减速长度L_s是指快中子从中子源发射开始到能量降低到超热中子的能量下限所经过的距离。为排除地层（尤其泥岩地层）热中子俘获截面的影响，采用对其不敏感的超热中子计数率。

根据中子减速的分组扩散理论，对于无限大的均匀介质点源模型，超热中子通量${\phi _{\rm{e}}}$与源距r的关系可以表示为：

式中：D_e表示扩散系数。

近、远探测器的计数率N₁、N₂与中子通量成正比，近、远探测器计数率比值R可以表示为：

式中：r₁表示短源距；r₂表示长源距。

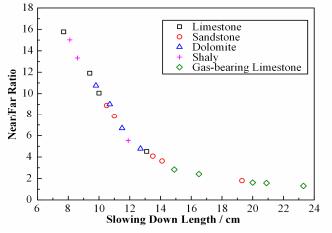
图 3为不同岩性及泥岩地层近、远计数率比值与中子减速长度的关系。从图 3中可以看到，含气地层测量点减速长度都较大，对应的计数率比值往往较低。不同岩性、泥岩和含气地层测量点几乎都在一条指数拟合曲线上，印证了式(2)的指数关系。当仪器的长、短源距固定时，近、远探测器计数率比值R反映的是地层快中子减速长度L_s值。

图 3

图 3 近、远探测器计数率比值与中子减速长度关系 Figure 3 Relationship between ratio of counting rate of near and far detectors and neutron slowing-down length

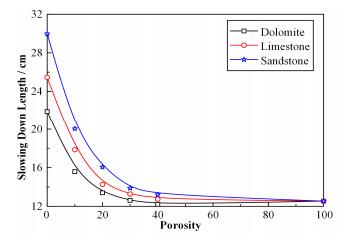
图 4为在不同岩性地层，快中子减速长度与地层孔隙度关系。可以看到在孔隙中充满饱和水时，减速长度是不同岩性地层孔隙度的函数。在孔隙为0时，砂岩减速长度最长，白云岩减速长度最短，在这种情况下，由于地层中无氢原子核，中子的减速过程只与地层岩性相关。随地层孔隙度的增加，三种岩性地层的中子减速长度迅速降低，差异也随之减小，说明在快中子的减速过程中，地层岩性有一定的影响，但氢原子核起至关重要的作用。

图 4

图 4 减速长度与孔隙度关系 Figure 4 Relationship between neutron slowing-down length and porosity

由核物理理论可知，对于无限大的均匀介质点源模型，快中子减速距离均方值$\overline {{R^2}} $为：

式中：${\lambda _{\rm{s}}}$为散射平均自由程，为中子与原子核连续发生两次散射之间的平均路程；E₀为中子源发射的快中子初始能量，其大小与中子源有关；E_f为减速到超热中子能量下限时的能量；$\zeta $为中子在地层中每次碰撞的平均对数能量损失；Σ_s为宏观散射截面；N为1cm³地层中原子核数，对于同一地层原子核数与体积密度${\rho _{\rm{b}}}$成正比关系；${\sigma _{\rm{s}}}$为微观散射截面。

地层中子的减速长度L_s定义为：

对低能量中子的减速地层中，氢元素是一个最重要的元素。在高能中子的减速中，上面结论将不成立。当中子处于1~14MeV高能量状态时，中子与地层原子核的非弹性散射是快中子失去能量的主要方式。氢元素对快中子的减速能力完全不同于超热中子，骨架原子的减速能力和氢原子比较接近。这时快中子的减速长度（或快中子通量）主要取决与地层原子密度和原子核种类。经过最初的非弹性碰撞后，快中子损失了足够多的能量。随后，快中子只能通过弹性散射继续损失能量，在这个能量区域，氢原子核与中子的散射作用占主导作用，决定了中子减速长度。

中子在地层中每次碰撞的平均对数能量损失$\zeta $可以表示为：

式中：n表示地层中元素的种类；${\zeta _i}$表示中子对地层中第i种元素核碰撞平均对数能量损失；N_i表示地层中第i种元素核数；σ_si表示对地层中第i种元素的微观散射截面。

对于中子在地层中每次碰撞的平均对数能量损失$\zeta $可以表示为：

式中：E为中子经过为一次弹性碰撞后的能量；A为元素原子核质量数。

随着地层元素平均对数能量损失$\zeta $的减小，中子与元素原子核碰撞的能量损失也会降低。图 5为地层中常见组成元素的碰撞平均对数能量损失与元素的原子核质量数关系。其中氢原子核的$\zeta_{\rm{H}} $=1，随元素的原子核质量数的增加，平均对数能量损失$\zeta $逐渐减小。可以看到，除氢元素外的其他元素的碰撞平均对数能量损失几乎要低氢原子核一个数量级。中子能量在0.01MeV以下时，地层中氢元素的弹性散射射线截面是其他元素的5~10倍，达到11 b左右，使氢原子在中子孔隙度测量中占主导地位。中子能量在0.01MeV以上时，所有元素的弹性散射截面随能量的增加而下降。同时在这个能量区间氢元素的非弹性散射截面为零，除氢以外其他元素的非弹性散射截面值约为弹性散射截面的一半。在14MeV时，弹性散射截面值都非常接近^[20]。因此氢原子核的散射截面${\sigma _{\rm{H}}}$要大于其他元素原子核截面。因此如果不考虑地层元素组成影响，式(6)可以简化为：

图 5

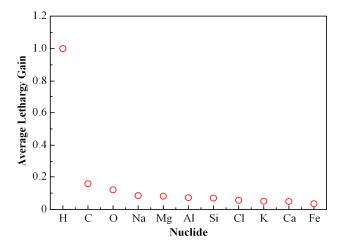
图 5 不同元素原子核的平均对数能量损失 Figure 5 The average lethargy gain of the nuclei of different elements

式中：a、b为常数，ab为地层除氢元素以外，其他所有元素的影响总和。对于式(8)分母$\sum\limits_1^n {{N_i}{\sigma _{{\rm{s}}i}}} $为多种元素的宏观截面之和，相当于地层的宏观散射截面Σ_s。

结合式(3)、(4)、(5)和(8)中子的计算长度L_s可以表示为：

将均匀地层假设为一种分子组成的，分子量为M，并设氢原子在该分子中的个数为r_H，则1cm³地层中氢原子个数N_H可以表示为：

式中：N_A为阿伏伽德罗常数。

根据含氢指数(I_H)定义：1cm³的任何岩石中氢原子数量与同样体积淡水中氢核的比值。对于孔隙中充满淡水的灰岩地层，含氢指数等于地层的孔隙度。可以得到任何密度为${\rho _{\rm{b}}}$，分子量为M，氢原子在该分子中的个数为r_H的地层含氢指数可以表示为：

对比式(10)、(11)，可以得到：

将式(12)带入式(9)中简化可以得到：

式中：k、c为常数。

热中子孔隙度仪器响应测量得到的基本参数为减速长度。从式(13)可以看到，在某一地层快中子的减速长度L_s可以表示为关于地层体积密度${\rho _{\rm{b}}}$、含氢指数I_H和快中子初始能量E₀的关系式。说明减速长度为地层体积密度、含氢指数、快中子初始能量三个影响因素的函数。减速长度分别与含氢指数、体积密度成反比，与快中子初始能量成正比关系。同时可以看到，地层体积密度、含氢指数、快中子初始能量三个影响因素相互独立，互不影响。

对于某一具体中子源，如D-T脉冲中子源作为随钻仪器的中子发生器测量地层中子孔隙度。中子源发射的快中子初始能量为14MeV。因此式(13)可以简化为：

式中：k’为常数。

根据式(2)可知，中子孔隙度仪器的近、远计数率比值响应与中子减速长度成指数关系。带入式(14)可以得到：

或：

式中：A、B、C、D、E、F为常数。

式(15)、(16)是在无限大的均匀介质点源模型中得到的计数率比值和体积密度与地层含氢指数的关系。当存在井眼时，可通过试验井测量或者仿真模拟的方法确定式(16)中有关常数。

从式(15)、(16)可以看到，通过对近、远探测器的计数率比值进行密度校正后可以得到仅与地层含氢指数相关的函数。图 6为经过密度校正前、后灰岩地层孔隙度灵敏度与地层含氢指数的关系。可以看到，在地层孔隙度为0%~40%内，孔隙度灵敏度都随孔隙度增加而快速降低。相对于未经校正的曲线，经过密度校正后的计数率比值对孔隙度的灵敏度显著提高。其中，在孔隙度为0%处，孔隙度灵敏度相近。孔隙度为40%时，孔隙度灵敏度提高了约3.6倍。孔隙度越大，灵敏度提高的越明显。

图 6

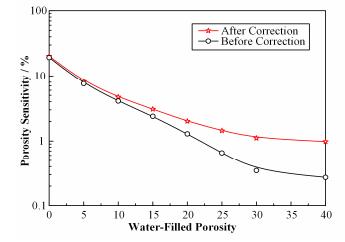
图 6 密度校正前、后对比 Figure 6 The porosity sensitivity value before and after density correction

当不考虑采样时间间隔影响时，仪器响应的孔隙度标准误差与孔隙度灵敏度成反比关系。经过密度校正不但能提高中子孔隙度灵敏度，也同时降低了孔隙度标准误差。提高了仪器在高孔隙度地层测量结果的准确度和精度。

图 7为经过密度校正后砂岩、灰岩、白云岩及泥岩地层计数率比值与地层含氢指数的关系。可以看到4种不同矿物地层分别经过密度校正后，计数率比值动态范围相近，孔隙度敏感度得到相应提高。白云岩、泥岩点非常接近灰岩响应曲线，三者基本重合。因此不需要进一步的岩性校正。因此在未知地层岩性的情况下，对计数率比值进行密度校正得到的地层含氢指数，可以基本消除泥岩效应和有效的降低地层岩性变化对仪器响应的影响。

图 7

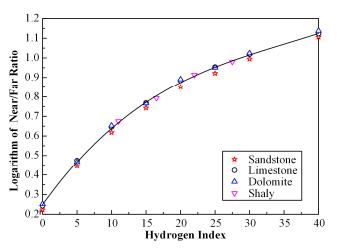
图 7 不同岩性地层密度校正后对比 Figure 7 The logarithm of ratio before and after density correction

在相同孔隙度岩性不同的地层中，使用脉冲中子孔隙度测量可能得到不同的视孔隙度。对于三种常见岩性地层中，分别要用不同计数率比值—孔隙度公式来计算视孔隙度。特别是当地层存在泥岩时，由于泥岩效应，得到的视孔隙度往往偏高。在标准刻度模型井中，对于灰岩、白云岩和砂岩进行了实验。由于缺少含泥岩的模型井，通过数值仿真模拟对不同孔隙度泥岩地层进行了模拟研究。分析了4种不同骨架地层校正前后的相应数据，如图 8所示。

图 8

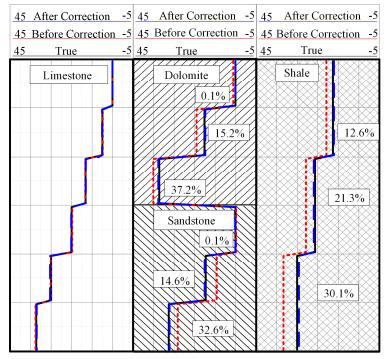
图 8 校正前后仪器响应对比 Figure 8 Comparison of the ratios before and after correction

图 8中长虚线曲线代表经过密度校正后得到的地层含氢指数，短虚线代表未进行密度校正的地层孔隙度，实线曲线代表地层真实孔隙度。第一道为灰岩地层，仪器在不同孔隙度的中响应结果。因仪器是在标准灰岩骨架地层刻度的，所以可以看到校正前后得到孔隙度和含氢指数重合。第二道为不同孔隙度的白云岩和砂岩地层。可以看到由于地层岩性效应的影响，使用灰岩刻度（计数率比值—孔隙度）响应公式计算得到的白云岩孔隙度要大于密度校正计算得到的地层含氢指数，砂岩孔隙度要小于密度校正计算得到的地层含氢指数。经过密度校正的含氢指数和地层含氢指数基本上一致。第三道为数值模拟设置的孔隙度分别为0%、10%和25%的泥岩地层。可以看到经过密度校正的含氢指数要比未经过密度校正的低，和地层含氢指数基本上一致。

由无限大均匀介质点源模型中得到，地层中子减速长度与地层的含氢指数、体积密度、快中子初始能量都相关。减速长度分别与含氢指数成反比、与体积密度成反比、与快中子初始能量成正比关系。由近/远探测器得到的计数率比值不仅与地层含氢指数相关，还与地层体积密度和快中子初始能量有关。

对灵敏度较差的D-T中子源计数率比值进行地层体积密度校正。可以显著地提高仪器孔隙度灵敏度和在高孔隙度地层测量结果的准确度和精度。

在未知地层岩性的情况下，对计数率比值进行密度校正得到的地层含氢指数，可以基本消除泥岩效应和有效地降低地层岩性变化对仪器响应的影响。最后进一步对不同岩性和泥岩地层分别进行了模型井和仿真模拟验证。