2. 中国科学院大学 北京 100049;
3. 华东理工大学 上海 200237;
4. 中国科学院上海高等研究院 国家蛋白质中心 上海 201210
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. East China University of Science and Technology, Shanghai 200237, China;
4. Nation Center for Protein Science Shanghai, Shanghai Advanced Research Institute, Shanghai 201210, China
一直以来,对纳米材料实现分子级别的调控[1],并结合传统工业手段使其组装成我们所需要的微观结构实现相应功能具有十分重大的意义[2]。在半导体材料工业发展中,利用传统光刻方法制造微电子器件的成本已经越来越高,往往认为周期长度小于某一临界值的半导体材料很难商业化使用[3],因此科学家们现在正在寻求其他技术以得到具有高分辨率、高通量、低成本的半导体器件。嵌段共聚物通过将两种互相排斥的成分通过化学链接方式结合在一起产生微相分离[4]而自组装形成具有一定规整性的纳米尺度结构[5]。这种周期性结构使嵌段共聚物在药物输送[6]、半导体器件[7]、激光光刻[8]及纳米粒子模板[9]等领域均具有重要作用。在这种微相分离的作用下,嵌段共聚物可在基底表面自组装形成诸如球状、柱状、螺旋及层状等多种结构[10]作为各类薄膜材料模板。目前,可利用腐蚀、电镀以及化学反应等方法在嵌段共聚物光刻模板上制备各类(硅、锗、氧化硅、砷化镓、钴[11-15])具有规整点、线排列的纳米结构材料。
自组装过程中,双嵌段共聚物的形貌主要由三个参数决定:两种嵌段体积分数(f)、总聚合度(N)以及表征两嵌段之间不兼容性的Flory-Huggins参数(χ)[16-18]。在最初自组装过程中,嵌段共聚物形貌往往只在亚微米结构中有序而无法达到半导体器件的要求,因此发展嵌段共聚物自组装成长程有序纳米结构方法学具有重大意义[8, 19]。在众多自组装方法中,热退火过程可以改变嵌段共聚物形貌、取向以及规整度等特性[20-21]。同时,与其他自组装方法相比,热退火方法具有设备要求简单、过程易控、无废气废液污染、自组装用时短等优点,更易于在工业设备中实用。
对于嵌段共聚物在不同条件(退火温度、薄膜厚度、不同气体氛围、嵌段比例、成膜方法)[20]下自组装成纳米结构,传统表征手法如透射电子显微镜(Transmission Electron Microscope, TEM)、原子力显微镜(Atomic Force Microscope, AFM)等对嵌段共聚物表面形貌、取向等具有良好的表征,然而这种常规离线状态下监测只能选取不连续的少量点观测其结构形貌变化,不具备时间分辨率,因而无法表征形貌连续转变过程以及相变细节等。原位研究嵌段共聚物退火过程,可以把握相分离细节以及观察形貌连续变化过程,对于精确制备具有纳米周期性结构的半导体材料以及理论验证均具有一定的意义。
在本次实验中,应用变温小角X射线散射(Small-angle X-ray Scattering, SAXS)技术对嵌段共聚物聚苯乙烯聚丙烯酸(Polystyrene-block-poly (acrylic acid)), PS-b-PAA)[22]相变过程进行了原位研究。通过对SAXS数据进行对距离分布函数(Pair Distance Distribution Function, PDDF)拟合分析,发现嵌段共聚物的构象随温度的转变过程。
1 实验部分三硫代碳酸酯终端的嵌段共聚物聚苯乙烯聚丙烯酸(PS-b-PAA, DDMAT terminated,产品编号:776351,PS:PAA= 3000:5000)购于美国Sigma-Aldrich试剂公司。SAXS实验在上海光源BL16B1线站上完成[23]。实验时选择的入射X射线的能量为10 keV,能量分辨率约为4×10-4,在样品处的光斑尺寸约为250 μm×470 μm,光通量1×1011 Phs·s-1。BL16B1实验站的X射线探测器为Mar165,像素尺寸79 μm×79 μm。利用胶原蛋白标准样品的标定,可以给出准确的样品到探测器的距离和q值的中心,本次实验的样品-探测器距离为1946 mm。实验采取透射SAXS模式,样品池的透光窗口使用Kapton膜封装,膜厚10 μm。在实验测量的q值范围内,没有观察到明显的SAXS信号。样品厚度约为0.5 mm。原位样品变温装置为英国Linkam公司的TS1500型热台,样品池紧贴于加热片处。为了确保样品温度在厚度方向的均匀性,根据实验经验,升温速率控制为0.3 ℃·min-1。实验采用了连续升温、快速测量的模式,样品曝光时间为10 s,因此在曝光时间内热台的温升约为0.05 ℃,因此,样品在曝光期间的温升在本实验中忽略不计。一维SAXS曲线使用自行开发的数据软件获得[24-25]。
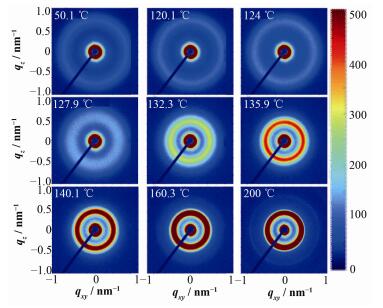
2 结果图 1是选取了在不同温度下得到的典型的二维SAXS图谱,温度分别为50.1 ℃、120.1 ℃、124.0 ℃、127.9 ℃、132.3 ℃、135.9 ℃、140.1 ℃、160.3 ℃和200 ℃。
|
图 1 PS-b-PAA在不同温度下得到的SAXS图谱 Figure 1 SAXS patterns of PS-b-PAA obtained at various temperatures |
从图 1可以看出,由于样品是粉末状,因此类似于粉末衍射,散射图样为均匀的环状,样品看不出明显的空间取向,可以视为各向同性的样品体系。在50~124 ℃,散射环的强度逐渐增强,但增幅较小;而升温至127.9 ℃时,散射强度进一步增加,同时散射环显著变宽。随着温度进一步升高至132.3℃和135.9 ℃时,散射强度进一步增加,散射环的半径变小同时环的宽度变窄;在140.1~ 200℃散射图样变化不是很明显。散射图样变化明显的温度区间为124~136 ℃。
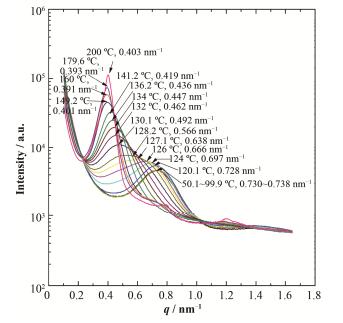
图 2是SAXS图谱进行积分得到的不同温度下的一维散射曲线。从图 2可以看到,在50.1~99.9℃,SAXS曲线变化不明显,散射峰位q≈0.73 nm-1。从99.9 ℃开始到128 ℃左右,散射曲线的峰值强度逐渐增强,散射峰位向低q区方向移动,并且伴有散射峰的宽化。温度继续升高至150 ℃左右,散射峰位继续向低q方向移动至q≈0.39 nm-1附近,同时散射强度继续增加,但是散射曲线的峰宽已经开始减少。150~200 ℃,尽管散射强度继续增加,但散射峰位已经基本不随温度变化了。另外,从150 ℃开始,除了主散射峰外,在其右侧,出现两个弱散射峰;200 ℃时,弱散射峰的位置在q≈0.8 nm-1和q≈1.2nm-1附近。根据散射峰随温度的变化情况,可以推断在120~150 ℃范围内,样品发生了相变。
|
图 2 PS-b-PAA在不同温度下得到的SAXS曲线 Figure 2 SAXS profiles of PS-b-PAA obtained at various temperatures |
由图 2可以看出,从150 ℃开始,除了q≈0.39nm-1附近的主散射峰外,在其右侧高q区,还存在着两个较弱散射峰;当温度达到200 ℃时,主散射峰q=0.40 nm-1,高q区的弱散射峰逐渐变得明显,分别位于q≈0.8 nm-1和q≈1.2 nm-1附近。因此,三个峰的峰间距都是Δq=0.4 nm-1,高q区的弱散射峰是粒子小角散射的二级和三级峰,并由此可以由L=2π/q估计出200 ℃时粒子的直径约为31.4 nm。
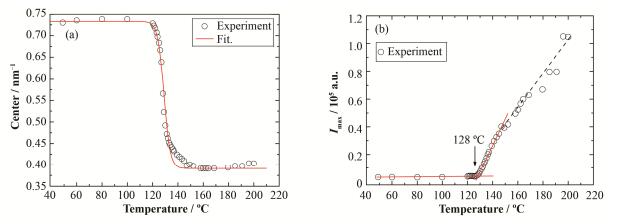
3.2 相变温度图 3为通过对图 2中散射峰进行拟合得到的散射峰峰位中心qc(图 3(a))和散射强度最大值Imax(图 3(b))随着温度变化的情况。图 3(a)中的实线是式(1)拟合的结果[26-28]。
|
图 3 SAXS峰中心位置随温度的变化情况(a)和散射峰最大值的温度依赖性(b) Figure 3 Temperature dependence of center of SAXS peak (a) and temperature dependence of maximum in intensity of SAXS peak (b) |
| $ {q_{\rm{c}}} = \frac{{\left( {B-A} \right)}}{2}\tanh \left( {\frac{{T-{T_{\rm{c}}}}}{{{T_{\rm{w}}}}}} \right) + {\rm{s}} $ | (1) |
式中:Tc为相变温度;B和A分别代表相变之前后处于平衡态的值;Tw为相变温度跨度;s为常数。拟合得到的相变温度为:Tc = (128±1) ℃;相变温度跨度为Tw = (5±1) ℃。图 3(b)中的实线是应用式(2)对散射强度最大值Imax的温度依赖性进行的线性拟合。
| $ {I_{\max }} = a \times T + {\rm{c}} $ | (2) |
式中:a代表Imax对温度依赖的程度。Tc是由相变前后对Imax的温度依赖性拟合所得线段延长线的交点得到的。通过拟合得到的abefore=(12±2) ℃-1,aafter=(1995±34) ℃-1;Tc是128 ℃,和式(1)对峰位中心qc的拟合结果一致。
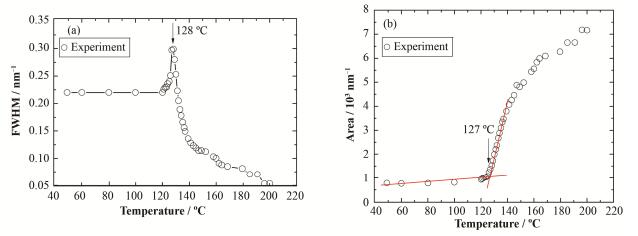
图 4(a)是SAXS峰的半高宽(Full width at half maxima, FMHW)随着温度的变化曲线。从图 4(a)可以看出,FMHW从121 ℃开始逐渐变大,128 ℃附近达到最大值,约131 ℃恢复到原有值,但随着温度的增加进一步变小。图 4(b)是SAXS峰的积分面积随温度的变化曲线。可以看出,127 ℃是一个明显的转变温度,这个值和图 4(a)中FMHW的转变温度128 ℃基本相符。
|
图 4 SAXS峰的FMHW随着温度的变化曲线(a)和散射峰面积分的温度依赖性(b) Figure 4 Temperature dependence of FMHW of SAXS peak (a) and temperature dependence of areal integrated intensity of SAXS peak (b) |
SAXS强度正比于空间的电子密度差的平方,其积分强度近似为[29-30]:
| $ \begin{array}{l} {I_q} = \int_V {\int_V {\rho \left( {{{\vec r}_1}} \right)} } \rho \left( {{{\vec r}_2}} \right){\text{e}^{-i\vec q \times \left( {{{\vec r}_1}-{{\vec r}_2}} \right)}}\text{d}{{\vec r}_1}\text{d}{{\vec r}_2}\\ \;\; = {\int_V {\left( {\delta \rho \left( {\vec r} \right)} \right)} ^2}{\text{e}^{-i\vec q \times \vec r}}\text{d}\vec r\\ \;\; = n{V_{\rm{p}}}\delta {\rho ^2}P\left( q \right)S\left( q \right) \end{array} $ | (3) |
式中:δρ是样品在空间内平均电子密度差;n为样品中的散射单体数目;Vp是散射单体体积;P(q)和S(q)分别为散射单体的形状因子和结构因子。对于稀疏体系(多为溶液和粉末),散射单体间的相互作用忽略。
对于形状和尺寸相同的单散射系来说,式(3)可积分为:
| $ I\left( q \right) = {\left( {\delta \rho } \right)^2}\int_0^\infty {\left\langle {{V^*}\left( {\vec r} \right)} \right\rangle 4\pi {r^2}\frac{{\sin \left( {qr} \right)}}{{qr}}{\rm{d}}r} $ | (4) |
其中:
| $ \left\langle {{V^*}\left( {\vec r} \right)} \right\rangle = \frac{1}{{4\pi }}\int_0^{4\pi } {{V^*}\left( {\vec r} \right){\rm{d}}\omega } $ |
代表将散射单体位移
| $ {\gamma _0}\left( r \right) = \frac{{\left\langle {{V^*}\left( {\vec r} \right)} \right\rangle }}{{{V_{\rm{p}}}}} $ |
则有:
| $ \begin{array}{l} I\left( q \right) = {\left( {\delta \rho } \right)^2}{V_{\rm{p}}}\int_0^\infty {{\gamma _0}\left( r \right)4\pi {r^2}\frac{{\sin \left( {qr} \right)}}{{qr}}{\rm{d}}r} \\ \;\;\;\;\;\;\; = {\left( {\delta \rho } \right)^2}\int_0^\infty {P\left( r \right)\frac{{\sin \left( {qr} \right)}}{{qr}}{\rm{d}}r} \end{array} $ | (5) |
式中:γ0(r)定义为PDDF,形状因子:
| $ P\left( r \right) = 4\pi {r^2}{V_{\rm{p}}}{\gamma _0}\left( r \right) $ | (6) |
因此,要想得到形状因子,只需得到PDDF即可。对本实验中得到的散射强度应用式(5)求和形式进行拟合,得到的拟合结果如图 5(a)所示。
|
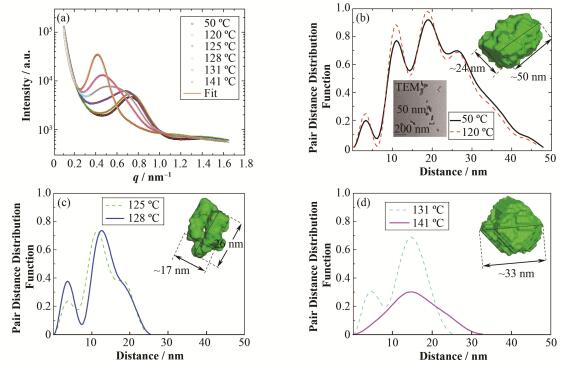
图 5 不同温度下的SAXS曲线和拟合结果(a)、得到的PDDF曲线:相变前的50 ℃和120 ℃ (b)、相变附近的125 ℃和128℃ (c)、相变后的131 ℃和141 ℃ (d)。插图为50 ℃ (b)、128 ℃ (c)和141 ℃ (d)下粒子的三维重构图,室温下的TEM图(b) Figure 5 Selected SAXS profiles obtained at various temperatures (a), the solid lines are the fit result of the data by Eq.(7); PDDF profiles obtained from fitting: 50 ℃ and 120 ℃ before the phase transition (b), 125 ℃ and 128 ℃ close the phase transition temperature (c), 131 ℃ and 141 ℃ after the phase transition (d). Insets are the three-dimensional graphics obtained from PDDF reconstructed: 50 ℃ (b), 128 ℃ (c) and 141 ℃ (d), and TEM image obtained at room temperature (b) |
| $ I\left( q \right) = {\left( {\delta \rho } \right)^2}{V_{\rm{p}}}\sum\nolimits_0^D {{\gamma _0}\left( r \right)4\pi {r^2}\Delta r\frac{{\sin \left( {qr} \right)}}{{qr}}} $ | (7) |
从图 5(a)可以看出,实验得到的散射强度(点)和拟合结果(实线)非常一致。通过拟合我们也得到了PDDF曲线(图 5(b)-(d)),50 ℃和120 ℃的PDDF曲线基本一致,为棒状体的特征曲线。图 5(b)-(d)中插图为基于PDDF特征曲线,应用DAMMIF程序[23],通过填充基本散射单元模型重构得到的三维立体图。图 5(b)中PDDF曲线的横轴最大值代表棒状体的长度(约48 nm),也是式(7)中的D值;PDDF曲线突起峰的最右侧最大值代表着棒状体的直径约为24 nm。图 5(b)中插图(下)为室温下的TEM图像(Tecnai G2F20S-TWIN,FEI公司,美国)。形状为棒状,长度约为50 nm,直径约为25 nm,和图 5(b)中模拟得到的结果一致。
随着温度升高至相变温度附近(125 ℃),棒状体出现孔洞(图 5(c)),孔洞直径即为PDDF曲线左方峰谷跨度,约为3.5 nm;当温度升至128 ℃,孔洞加大约4 nm,并且伴随着横坐标20 nm附近棒状特征峰的减弱;当温度升值131 ℃,20 nm附近棒状的特征峰基本消失,转变为直径25 nm左右有孔洞的球,内部空心约为5 nm;继续升温跨过相变温度区域的141 ℃,PDDF曲线转变为球形的特征曲线(图 6(d)),直径为35 nm左右。当然,可以看出(图 5(d)插图)这并不是一个标准的球形,而是一个类球形的多面体。随着温度的继续升高,粒子的形状得以进一步规整,SAXS的多级散射峰也逐渐变得明显(图 2)。
4 结语本文应用SAXS技术原位研究了PS3000-b- PAA5000温度场下的自组装过程。随着温度的升高,散射峰位从q≈0.73 nm-1逐渐向低q区域移动,并伴随着散射峰FWHM的增加,在128 ℃附近达到极值。当温度进一步升高,散射峰位继续向低q区域移动,但FWHM逐渐减少。通过对散射峰特征值(峰位、Imax、FWHM和积分强度)的拟合发现,PS3000-b-PAA5000的相变温度为128 ℃,相变温度跨度为5℃。通过对SAXS的I-q曲线进行PDDF拟合分析,一个可能的自组装过程进一步被发现。PS3000-b-PAA5000自组装相变前为类棒状体,随着温度升高棒状体出现孔洞,棒状体变短,并逐渐由棒状转变为带孔的球状体,并逐渐最终长大为直径30 nm左右的类球体。
| [1] |
Haynes C L, Van Duyne R P. Nanosphere lithography:a versatile nanofabrication tool for studies of size-dependent nanoparticle optics[J]. The Journal of Physical Chemistry B, 2001, 105: 5599-5611. DOI:10.1021/jp010657m |
| [2] |
Gates B D, Xu Q, Stewart M, et al. New approaches to nanofabrication:molding, printing, and other techniques[J]. Chemical Reviews, 2005, 105(4): 1171-1196. DOI:10.1021/cr030076o |
| [3] |
Sanders D P. Advances in patterning materials for 193 nm immersion lithography[J]. Chemical Reviews, 2010, 110(1): 321-360. DOI:10.1021/cr900244n |
| [4] |
Bates F S. Polymer-polymer phase behavior[J]. Science, 1991, 251(4996): 898-905. DOI:10.1126/science.251.4996.898 |
| [5] |
Bates F S, Fredrickson G H. Block copolymer thermodynamics:theory and experiment[J]. Annual Review of Physical Chemistry, 1990, 41(1): 525-557. DOI:10.1146/annurev.pc.41.100190.002521 |
| [6] |
Gaucher G, Dufresne M H, Sant V P, et al. Block copolymer micelles:preparation, characterization and application in drug delivery[J]. Journal of Controlled Release, 2005, 109(1-3): 169-188. DOI:10.1016/j.jconrel.2005.09.034 |
| [7] |
Kim H C, Park S M, Hinsberg W D. Block copolymer based nanostructures:materials, processes, and applications to electronics[J]. Chemical Reviews, 2009, 110(1): 146-177. DOI:10.1021/cr900159v |
| [8] |
Bates C M, Maher M J, Janes D W, et al. Block copolymer lithography[J]. Macromolecules, 2013, 47(1): 2-12. DOI:10.1021/ma401762n |
| [9] |
Smarsly B, Grosso D, Brezesinski T, et al. Highly crystalline cubic mesoporous TiO2 with 10-nm pore diameter made with a new block copolymer template[J]. Chemistry of Materials, 2004, 16(15): 2948-2952. DOI:10.1021/cm0495966 |
| [10] |
Bates F S, Schulz M F, Khandpur A K, et al. Fluctuations, conformational asymmetry and block copolymer phase behaviour[J]. Faraday Discussions, 1994, 98: 7-18. DOI:10.1039/FD9949800007 |
| [11] |
Chang S W, Chuang V P, Boles S T, et al. Densely packed arrays of ultra-high-aspect-ratio silicon nanowires fabricated using block-copolymer lithography and metal-assisted etching[J]. Advanced Functional Materials, 2009, 19(15): 2495-2500. DOI:10.1002/adfm.200900181 |
| [12] |
Aizawa M, Buriak J M. Block copolymer-templated chemistry on Si, Ge, InP, and GaAs surfaces[J]. Journal of the American Chemical Society, 2005, 127(25): 8932-8933. DOI:10.1021/ja052281m |
| [13] |
Park S, Kim B, Wang J Y, et al. Fabrication of highly ordered silicon oxide dots and stripes from block copolymer thin films[J]. Advanced Materials, 2008, 20(4): 681-685. DOI:10.1002/adma.200701997 |
| [14] |
Li R R, Dapkus P D, Thompson M E, et al. Dense arrays of ordered GaAs nanostructures by selective area growth on substrates patterned by block copolymer lithography[J]. Applied Physics Letters, 2000, 76(13): 1689-1691. DOI:10.1063/1.126137 |
| [15] |
Cheng J Y, Ross C A, Chan V Z H, et al. Formation of a cobalt magnetic dot array via block copolymer lithography[J]. Advanced Materials, 2001, 13(15): 1174-1178. DOI:10.1002/1521-4095(200108)13:15<1174:AID-ADMA1174>3.0.CO;2-Q |
| [16] |
Helfand E, Tagami Y. Theory of the interface between immiscible polymers Ⅱ[J]. The Journal of Chemical Physics, 1972, 56(7): 3592-3601. DOI:10.1063/1.1677735 |
| [17] |
Helfand E. Theory of inhomogeneous polymers:fundamentals of the Gaussian random-walk model[J]. The Journal of Chemical Physics, 1975, 62(3): 999-1005. DOI:10.1063/1.430517 |
| [18] |
Drolet F, Fredrickson G H. Combinatorial screening of complex block copolymer assembly with self-consistent field theory[J]. Physical Review Letters, 1999, 83(21): 4317. DOI:10.1103/PhysRevLett.83.4317 |
| [19] |
Tang C, Lennon E M, Fredrickson G H, et al. Evolution of block copolymer lithography to highly ordered square arrays[J]. Science, 2008, 322(5900): 429-432. DOI:10.1126/science.1162950 |
| [20] |
Albert J N L, Epps Ⅲ T H. Self-assembly of block copolymer thin films[J]. Materials Today, 2010, 13(6): 24-33. DOI:10.1016/S1369-7021(10)70106-1 |
| [21] |
Welander A M, Kang H, Stuen K O, et al. Rapid directed assembly of block copolymer films at elevated temperatures[J]. Macromolecules, 2008, 41(8): 2759-2761. DOI:10.1021/ma800056s |
| [22] |
金鑫, 杨春明, 滑文强, 等. PS3000-b-PAA5000球形胶束温度效应的原位X射线小角散射技术研究[J]. 物理学报, 2018, 67(4): 048301. JIN Xin, YANG Chunming, HUA Wenqiang, et al. Temperature dependence of spherical micelles of PS3000-b-PAA5000 studied by in-situ small angle X-ray scattering[J]. Acta Physica Sinica, 2018, 67(4): 048301. DOI:10.7498/aps.67.048301 |
| [23] |
Tian F, Li X H, Wang Y Z, et al. Small angle X-ray scattering beamline at SSRF[J]. Nuclear Science and Techniques, 2015, 26(3): 030101. DOI:10.13538/j.1001-8042/nst.26.030101 |
| [24] |
Zhao N, Yang C, Zhang Q, et al. A general model for estimating the ordering of mesoporous film by grazing incidence small angle X-ray scattering[J]. Journal of Applied Physics, 2014, 115(20): 204311. DOI:10.1063/1.4875662 |
| [25] |
Zhao N, Yang C, Wang Y, et al. Probing the surface microstructure of layer-by-layer self-assembly chitosan/poly (l-glutamic acid) multilayers:a grazing-incidence small-angle X-ray scattering study[J]. Materials Science and Engineering:C, 2016, 58: 352-358. DOI:10.1016/j.msec.2015.08.048 |
| [26] |
Dalnoki-Veress K, Forrest J A, Murray C, et al. Molecular weight dependence of reductions in the glass transition temperature of thin, freely standing polymer films[J]. Physical Review E, 2001, 63(3): 031801. DOI:10.1103/PhysRevE.63.031801 |
| [27] |
Yang C, Onitsuka R, Takahashi I. Confinement effects on glass transition temperature, transition breadth, and linear expansivity:an ultraslow X-ray reflectivity study on supported ultrathin polystyrene films[J]. The European Physical Journal E, 2013, 36(6): 66. DOI:10.1140/epje/i2013-13066-3 |
| [28] |
Yang C, Ishimoto K, Matsuura S, et al. Depth-dependent inhomogeneous characteristics in supported glassy polystyrene films revealed by ultra-low X-ray reflectivity measurements[J]. Polymer Journal, 2014, 46(12): 873. DOI:10.1038/pj.2014.80 |
| [29] |
Roe R J. Methods of X-ray and neutron scattering in polymer science[M]. Oxford: Oxford University Press on Demand, 2000, 739.
|
| [30] |
孟昭富. 小角X射线散射理论及应用[M]. 长春: 吉林科学技术出版社, 1996. MENG Zhaofu. Small angle X-ray scattering theory and the applications[M]. Changchun: Jilin Science and Technology Press, 1996. |


