基于指数变换的三维六角形节块法动力学程序开发及验证

引用本文 [复制中英文]

程懋松, 林铭, 左献迪, 戴志敏. 基于指数变换的三维六角形节块法动力学程序开发及验证[J]. 核技术, 2018, 41(6): 060604. DOI: 10.11889/j.0253-3219.2018.hjs.41.060604.

[复制中文]

CHENG Maosong, LIN Ming, ZUO Xiandi, DAI Zhimin. Development and validation of a three-dimensional hexagonal nodal time-spatial kinetics code based on exponential transform[J]. Nuclear Techniques, 2018, 41(6): 060604. DOI: 10.11889/j.0253-3219.2018.hjs.41.060604.

[复制英文]

基金项目

中国科学院战略先导科技专项（No.XD02001005）资助

第一作者

程懋松, 男, 1981年出生, 2014年于中国科学院上海应用物理研究所获博士学位, 研究领域为核能科学与工程

文章历史

收稿日期: 2017-11-30
修回日期: 2018-01-19

Contents Abstract Full text Figures/Tables PDF

基于指数变换的三维六角形节块法动力学程序开发及验证

程懋松¹, 林铭^1,2, 左献迪^1,2, 戴志敏¹

1. 中国科学院上海应用物理研究所嘉定园区上海 201800;
2. 中国科学院大学北京 100049

收稿日期: 2017-11-30; 修回日期: 2018-01-19

中国科学院战略先导科技专项（No.XD02001005）资助

第一作者: 程懋松, 男, 1981年出生, 2014年于中国科学院上海应用物理研究所获博士学位, 研究领域为核能科学与工程.

摘要: 熔盐堆是第四代先进反应堆6个候选堆型之一，包括液态燃料熔盐堆和固态燃料熔盐堆，其中固态燃料熔盐堆采用高温熔盐作为冷却剂，具备高温、常压、高功率密度等优点，在固有安全性以及经济性上具有极大的优势和潜力。为了开展六角形燃料组件熔盐冷却先进高温堆瞬态分析和安全评估，基于指数变换和六角形节块展开法，开发了三维时空动力学程序TCORE3D-HEX。选取了两个俄罗斯VVER型压水堆国际基准题算例，通过对比及分析国际上几种适用于六角形几何的时空动力学程序，验证TCORE3D-HEX程序的正确性。结果表明：基于指数变换和六角形节块法开发的三维时空动力学程序数值计算结果与国际上其他程序计算结果符合得很好，初步验证了程序的正确性，为钍基熔盐堆核能系统（Thorium Molten Salt Reactor，TMSR）设计提供了可靠的分析和评估工具。

关键词: 固态燃料熔盐堆指数变换六角形节块展开法时空动力学

Development and validation of a three-dimensional hexagonal nodal time-spatial kinetics code based on exponential transform

CHENG Maosong¹ , LIN Ming^1,2 , ZUO Xiandi^1,2 , DAI Zhimin¹

1. Shanghai Institute of Applied Physics, Chinese Academy of Sciences, Jiading Campus, Shanghai 201800, China;
2. University of Chinese Academy of Sciences, Beijing 100049, China

Received date: 2017-11-30; accepted date: 2018-01-19

Supported by Strategic Pilot Science and Technology Project of Chinese Academy of Sciences (No.XD02001005)

First author: CHENG Maosong, male, born in 1981, graduated from Shanghai Institute of Applied Physics, Chinese Academy of Sciences with a doctoral degree in 2014, focusing on nuclear energy science and engineering.

Abstract: Background: Molten salt reactor is one of the six Generation Ⅳ advanced reactor concepts selected by Generation Ⅳ International Forum (GIF), which can be divided into liquid-fueled and solid-fueled molten salt reactor. The solid-fueled molten salt reactor uses high-temperature liquid-salt as coolant and is provided with features of high-temperature, low-pressure and high-power density, as well as great advantage and potential in inherent safety. Purpose: This study aims to develop and validate a three-dimensional time-spatial kinetics code named TCORE3D-HEX which can be used to carry out transient analysis and safety assessment of molten salt-cooled reactor with hexagonal fuel assembly. Methods: The exponential transform and hexagonal nodal expand methods are applied in the TCORE3D-HEX kinetics code. Two VVER (Vodo-Vodyanoi Energetichesky Reaktor) international benchmarks are selected to validate the validity of the TCORE3D-HEX code by comparing with several three-dimensional hexagonal nodal time-spatial kinetics codes. Results: The results indicate that the numerical result of the TCORE3D-HEX code are in good agreement with that of other kinetics codes. Conclusion: The developed kinetics code is validated on VVER pressurized water reactor (PWR), and will be a reliable analytical and assessment tool for the design of innovative molten salt-cooled reactor in thorium molten salt reactor (TMSR).

Key Words: Molten salt-cooled reactor Exponential transform Hexagonal nodal method Time-spatial kinetics

熔盐堆最早在1947年由美国橡树岭国家实验室(Oak Ridge National Laboratory, ORNL)提出，经过几十年的发展，熔盐堆的概念现在已经扩展为两类主要的反应堆：液态燃料熔盐堆和固态燃料熔盐堆（也称为熔盐冷却高温堆）^[1]。液态燃料熔盐堆将燃料盐直接溶于高温熔盐冷却剂中，其中液态高温熔盐既用作冷却剂，也作为核燃料的载体。固体燃料熔盐堆采用熔盐作为冷却剂，选用传统或者新型的固态燃料。

2004年，美国ORNL、加州大学伯克利分校(University of California, Berkeley, UCB)、圣地亚哥国家实验室(Sandia National Laboratories, SNL)重新评估熔盐堆的研究内容和技术路线，决定选择固体燃料、高温熔盐作为冷却剂，提出了棱柱形先进高温堆概念设计^[2]。美国ORNL于2015和2016年分别完成和发布了氟盐冷却高温示范堆的初步要点设计和要点设计^[3-4]。

中国科学院上海应用物理所为主承担了的“未来先进核裂变能-钍基熔盐堆核能系统(Thorium Molten Salt Reactor, TMSR)”首批战略性先导科技专项，正积极开展各种类型熔盐堆概念设计和工程设计^[5]。固体燃料熔盐堆仅将熔盐作为冷却剂传输热量，燃料可以采用各种形式的固态燃料元件，包括：球型、棱柱型、板型和棒型。其中除了球形燃料外，选用板型和棒型燃料元件的熔盐冷却先进高温堆，燃料组件基本采用六角棱柱形。节块展开法具有计算速度快、能给出高精度的节块平均通量等优点，广泛应用于核设计和动力学分析^[6]。指数变换方法能够减少中子通量离散过程中的截断误差，减少计算引入的系统误差，能够适应反应堆物理提出的新的“高保真”要求。因此，基于指数变换和六角形节块展开法，开发三维时空动力学程序具有广泛的适用性，可用于所有采用六角棱柱形组件的熔盐冷却固态燃料熔盐堆三维时空动力学计算分析，以满足TMSR专项熔盐冷却六角棱柱形固态燃料熔盐堆瞬态分析和安全评估需求。

1 理论模型 1.1 中子动力学模型

在节块n内，假设在每个节块内具有均匀化的等效参数，一般的两群中子扩散方程表示为^[7]：

$ \begin{array}{l} \frac{{\partial \mathit{\Phi} _1^n(r, t)}}{{v_1^n\partial t}}-\nabla D_1^n(t)\nabla \mathit{\Phi} _1^n(r, t) + \mathit{\Sigma} _r^n(t)\mathit{\Phi} _1^n(r, t) = \\ \begin{array}{*{20}{c}} {}&{} \end{array}\frac{1}{{{k_{{\rm{eff}}}}}}\sum\limits_{g = 1}^2 {(1-\beta _g^n)\nu \mathit{\Sigma} _{f, g}^n(t)\mathit{\Phi} _g^n(r, t)} + \\ \begin{array}{*{20}{c}} {}&{} \end{array}\sum\limits_{j = 1}^M {\lambda _j^nC_j^n(r, t)} + S_{{\rm{ext}}}^n(r) \end{array} $

(1)

$ \begin{array}{l} \frac{{\partial \mathit{\Phi} _2^n(r, t)}}{{v_2^n\partial t}} - \nabla D_2^n(t)\nabla \mathit{\Phi} _2^n(r, t) + \mathit{\Sigma} _a^n(t)\mathit{\Phi} _2^n(r, t) = \\ \begin{array}{*{20}{c}} {}&{} \end{array}\mathit{\Sigma} _s^n(t)\mathit{\Phi} _1^n(r, t) \end{array} $

(2)

$ \begin{array}{l} \frac{{\partial C_j^n\left( {r, t} \right)}}{{\partial t}} = \\ \begin{array}{*{20}{c}} {}&{} \end{array}\frac{1}{{{k_{{\rm{eff}}}}}}\sum\limits_{g = 1}^2 {\beta _{g, j}^n\nu \mathit{\Sigma}_{f, g}^n\left( t \right)\mathit{\Phi} _g^n\left( {r, t} \right)}-\lambda _j^nC_j^n\left( {r, t} \right) \end{array} $

(3)

其中：$\beta _g^n = \sum\limits_{j = 1}^M {\beta _{g, j}^n} {, ^{}}g = 1, 2 $，$ j = 1, 2, ..., M$；$\mathit{\Phi} _g^n$表示第g群节块n平均中子通量；D_gⁿ表示第g群节块n中子扩展系数；∑_rⁿ、∑_sⁿ、∑_aⁿ和∑_{f, g}ⁿ分别表示节块n宏观移出截面、宏观散射截面、宏观吸收截面和第g群裂变截面；v_gⁿ表示第g群节块n中子平均速度；C_jⁿ、λ_jⁿ和β_{g, j}ⁿ分别表示节块n内第j群缓发中子先驱核浓度、第j群缓发中子衰变常数和第g能群j群缓发中子衰变份额；S_extⁿ表示外源；k_eff表示初始稳态有效增殖因子；r和t分别表示位置和时间。

1.2 指数变换法

将通量表示为：

$ \mathit{\Phi} _g^n\left( {r, t'} \right) = \exp [{\mathit{\Theta} ^n}(t'-t + \Delta t)] \cdot \varphi _g^n\left( {r, t'} \right) $

(4)

其中：$\Delta t$为时间步长，$t-\Delta t \le t' \le t $，且满足：

$ \mathit{\Phi} _g^n\left( {r, t-\Delta t} \right) = \varphi _g^n\left( {r, t-\Delta t} \right) $

(5)

因此，通量的时间导数可以表示为：

$ \begin{array}{l} \frac{{{\rm{d}}\mathit{\Phi} _g^n\left( {r, t} \right)}}{{{\rm{d}}t}} \approx \\ \frac{1}{{\Delta t}} \cdot \left[{\left( {1 + {\mathit{\Theta} ^n}\Delta t} \right) \cdot \mathit{\Phi} _g^n\left( {r, t} \right)-\exp \left( {{\mathit{\Theta} ^n}\Delta t} \right) \cdot \mathit{\Phi} _g^n\left( {r, t-\Delta t} \right)} \right] \end{array} $

(6)

其中：$ {\mathit{\Theta} ^n}$可以通过节块平均通量计算获得：

$ {\mathit{\Theta} ^n} = \frac{1}{{\Delta t}} \cdot \ln \frac{{\sum\limits_{g = 1}^2 {\mathit{\overline \Phi} _g^n\left( t \right)} }}{{\sum\limits_{g = 1}^2 {\mathit{\overline \Phi} _g^n\left( {t-\Delta t} \right)} }} $

(7)

式中：$\mathit{ \overline \Phi} _g^n$表示节块n内的节块平均通量。

缓发中子先驱核积分可得：

$ \begin{array}{c} C_j^n\left( {r, t} \right) = C_j^n\left( {r, t - \Delta t} \right) \cdot \exp \left( { - \lambda _j^n\Delta t} \right) + \\ \;\;\frac{{1 - \exp \left[{-\left( {\lambda _j^n + {\mathit{\Theta} ^n}} \right)\Delta t} \right]}}{{\lambda _j^n + {\mathit{\Theta} ^n}}} \cdot \frac{1}{{{k_{\rm{eff}}}}} \cdot \\ \;\;\sum\limits_{g = 1}^2 {\beta _{g, j}^n\nu \mathit{\Sigma}_{f, g}^n\left( t \right)\mathit{\Phi} _g^n\left( {r, t} \right)} \end{array} $

(8)

将式(6)和(8)代入式(1)和(2)中，最终可得简化形式的两群中子守恒方程：

$ \nabla J_g^n(r, t) + \mathit{\tilde \Sigma {}}_g^n(t)\mathit{\Phi} _g^n(r, t) = S_g^n\left( {r, t} \right) $

(9)

其中：

$ \nabla J_g^n(r, t) =- D_g^n\left( t \right)\nabla \mathit{\Phi} _g^n\left( {r, t} \right)\\ \mathit{\tilde \Sigma} {}_1^n(t){\rm{ = }}\mathit{\Sigma} _r^n(t) + \frac{{1 + {\mathit{\Theta} ^n}\Delta t}}{{v_1^n\Delta t}}\\ \mathit{\tilde \Sigma} {}_2^n(t){\rm{ = }}\mathit{\Sigma} _a^n(t) + \frac{{1 + {\mathit{\Theta} ^n}\Delta t}}{{v_2^n\Delta t}}\\ S_1^n\left( {r, t} \right) = \frac{1}{{{k_{eff}}}}\sum\limits_{g = 1}^2 {\left( {1- \sum\limits_{j = 1}^M {\beta _{g, j}^n\eta _j^n} } \right)\nu \mathit{\Sigma} _{f, g}^n(t)\mathit{\Phi} _g^n\left( {r, t} \right)} + \\ \;\sum\limits_{j = 1}^M {\lambda _j^nC_j^n\left( {r, t- \Delta t} \right)\exp \left( { - \lambda _j^n\Delta t} \right)} + \\ \;\frac{{\exp ({\mathit{\Theta} ^n}\Delta t)}}{{v_1^n\Delta t}} \cdot \mathit{\Phi} _1^n\left( {r, t - \Delta t} \right) + S_{{\rm{ext}}}^n(r)\\ \eta _j^n = \frac{{{\mathit{\Theta} ^n} + \lambda _j^n\exp \left[{-\left( {\lambda _j^n + {\mathit{\Theta} ^n}} \right)\Delta t} \right]}}{{\lambda _j^n + {\mathit{\Theta} ^n}}}\\ S_2^n\left( {r, t} \right) = \mathit{\Sigma} _s^n(t)\mathit{\Phi} _1^n\left( {r, t} \right) + \frac{{\exp ({\mathit{\Theta} ^n}\Delta t)}}{{v_2^n\Delta t}} \cdot \mathit{\Phi} _2^n\left( {r, t -\Delta t} \right) $

瞬态和稳态方程可以表示为相同的形式，因此，求解以上方程组，具体空间离散方法相同，求解过程也采用相同的求解算法。

1.3 六角形棱柱节块展开法

如图 1所示，在六角形棱柱几何中，节块体积${V^n} = \frac{{\sqrt 3 }}{2}{d^2} \cdot a_z^n$，其中：d表示六边形两条对边之间的距离；$a_z^n$表示节块n的高度。在轴向，节块节点位于坐标${z_0} = {z_i} - \frac{{{a_z}}}{2}$和${z_1} = {z_i} + \frac{{{a_z}}}{2}$之间。

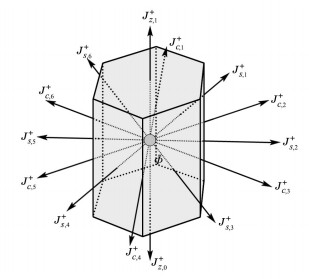
图 1 六角形棱柱节块几何示意图 Figure 1 Hexagonal node with directions of outgoing partial currents

1.3.1 六角形平面积分

沿着轴向z积分方程(9)，可得能群g的二维方程：

$ \begin{array}{l} - {D_g}\left( t \right)\left( {\frac{{{\partial ^2}}}{{\partial {x^2}}} + \frac{{{\partial ^2}}}{{\partial {y^2}}}} \right){{\mathit{\bar \Phi} }_g}\left( {x, y, t} \right) + {{\mathit{\tilde \Sigma} }_g}\left( t \right){{\mathit{\bar \Phi} }_g}\left( {x, y, t} \right) = \\ \begin{array}{*{20}{c}} {}&{}&{} \end{array}{{\bar Q}_g}\left( {x, y, t} \right) \end{array} $

(10)

其中：

$ {\bar Q_g}\left( {x, y, t} \right) = {\bar S_g}\left( {x, y, t} \right) - {\bar L_g}\left( {x, y, t} \right) $

(11)

式中：${\mathit{\bar \Phi} _g}\left( {x, y, t} \right) $为平均通量；${\bar S_g}\left( {x, y, t} \right)$为平均源和；${\bar L_g}\left( {x, y, t} \right)$为平均横向积分泄漏项。

定义：

$ \begin{array}{l} x' = 2\frac{x}{d}, \;y' = 2\frac{y}{d}, \;D' = 2\frac{D}{d}, \;\mathit{\Sigma} ' = \mathit{\Sigma} \cdot \frac{d}{2}, \\ \bar S' = \bar S \cdot \frac{d}{2}, \;\bar L' = \bar L \cdot \frac{d}{2}, \;\bar Q' = \bar Q \cdot \frac{d}{2} \end{array} $

(12)

六边形平面内的通量可以通过两阶多项式和指数函数展开^[7]。根据式(12)，通量表示为：

$ \begin{array}{c} \mathit{\bar \Phi} \left( {x', y', t} \right) \approx \sum\limits_{i = 0}^5 {{c_i}\left( t \right) \cdot {f_i}\left( {x', y'} \right)} + \\ \;\sum\limits_{k = 1}^6 {{a_{s, k}}\left( t \right) \cdot \exp \left[{B'\left( {{e_{s, k}} \cdot {{r'}_{x, y}}} \right)} \right]} + \\ \;\sum\limits_{k = 1}^6 {{a_{c, k}}\left( t \right) \cdot \exp \left[{B'\left( {{e_{c, k}} \cdot {{r'}_{x, y}}} \right)} \right]} \end{array} $

(13)

式中：矢量${r'_{x, y}} = \left( {x', y'} \right) $；单位矢量e_{s, k}是从六边形中心指向边线的中点；单位矢量e_{c, k}表示从六边形的中点指向六边形的顶角，具体如图 2所示。

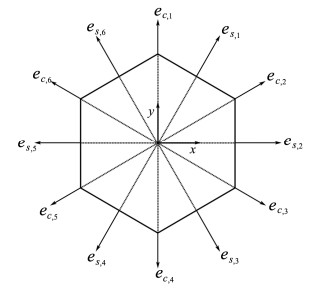
图 2 六边形单位矢量e_{s, k}和e_{c, k} Figure 2 Hexagon with the considered directions e_{s, k} and e_{c, k}

曲率为$B' = \sqrt {\frac{{\mathit{\Sigma} '}}{{D'}}} $，多项式${f_i}\left( {x', y'} \right)$表示为：

$ \begin{array}{l} {f_0} = \frac{1}{{{N_0}}}, {f_1} = \frac{{x'}}{{{N_1}}}, {f_2} = \frac{{y'}}{{{N_2}}}, \\ {f_3} = \frac{1}{{{N_3}}}\left( {{{x'}^2} + {{y'}^2} - \frac{5}{9}} \right), {f_4} = \frac{{{{x'}^2} - {{y'}^2}}}{{{N_4}}}, {f_5} = \frac{{x'y'}}{{{N_5}}} \end{array} $

(14)

多项式${f_i}\left( {x', y'} \right)$和归一化因子N_i满足正交关系：

$ \int\limits_{{{I'}_{{\rm{hex}}}}} {{f_i}\left( {x', y'} \right){f_j}\left( {x', y'} \right){\rm{d}}y'{\rm{d}}x'} = {\delta _{ij}} $

(15)

式中：${I'_{{\rm{hex}}}}$表示六边形的面积。

缓发中子先驱核${\bar C_j}\left( {x', y', t} \right)$通过以下多项式展开逼近：

$ {\bar C_j}\left( {x', y', t} \right) \approx \sum\limits_{i = 0}^5 {{c_{{\rm{pre}}, j, i}}\left( t \right) \cdot {f_i}\left( {x', y'} \right)} $

(16)

泄漏项$\bar L\left( {x', y', t} \right)$通过以下多项式展开逼近：

$ \bar L\left( {x', y', t} \right) \approx \sum\limits_{i = 0}^5 {{l_i}\left( t \right){f_i}\left( {x', y'} \right)} $

(17)

将式(13)、(16)和(17)展开带入式(10)，获得高阶展开系数方程：

$ \begin{array}{l} \left( {\mathit{\Sigma} _r^n\left( t \right) + \frac{{{\mathit{\Theta} ^n}}}{{v_1^{}}}} \right)c_{1, i}^n\left( t \right) = \\ \quad \frac{1}{{{k_{{\rm{eff}}}}}}\sum\limits_{g = 1}^2 {\left( {1-\sum\limits_{j = 1}^M {\beta _{g, j}^n\eta _j^n} } \right)\nu \mathit{\Sigma} _{f, g}^n(t)c_{g, i}^n\left( t \right)} {\rm{ + }}\\ \quad \sum\limits_{j = 1}^M {\lambda _j^nc_{{\rm{pre}}, j, i}^n\left( {t-\Delta t} \right)\exp \left( {-\lambda _j^n\Delta t} \right)} - \\ \quad l_{1, i}^n\left( t \right)\left( {\mathit{\Sigma} _a^n\left( t \right) + \frac{{{\mathit{\Theta} ^n}\Delta t}}{{v_2^{}}}} \right)c_{2, i}^n\left( t \right) = \\ \quad \mathit{\Sigma} _s^n(t)c_{1, i}^n\left( t \right) - l_{2, i}^n\left( t \right) \end{array} $

(18)

式(13)指数函数的系数可以通过节块间界面条件或者系统外边界的边界条件获得。在扩散近似中，在e方向进出节块的中子流分别表示为J^-和J⁺。边平均或者角平均中子流表示为：

$ {J^ \pm } = \frac{1}{2} \cdot \left( {\frac{1}{2}\mathit{\Phi} \pm \left( {eJ} \right)} \right) $

(19)

式中：Φ表示边通量或者角通量；J表示边或者角净中子流。将通量展开方程(13)和菲克定律$ J_g^n\left( {r, t} \right) =-D_g^n\left( t \right)\nabla \mathit{\Phi} _g^n\left( {r, t} \right)$带入，所有边和角偏中子流通过式(20)表示：

$ \begin{array}{l} J_s^ \pm = \mathit{\Pi} _s^ \pm C + {\rm E}_{ss}^ \pm {A_s} + {\rm E}_{sc}^ \pm {A_c}\\ J_c^ \pm = \mathit{\Pi} _c^ \pm C + {\rm E}_{cs}^ \pm {A_s} + {\rm E}_{cc}^ \pm {A_c} \end{array} $

(20)

式中：矢量C、A_s、A_c分别表示式(13)展开系数c_i、a_{s, k}、a_{c, k}；矢量$J_s^ \pm $和$J_c^ \pm $分别表示边偏中子流$J_{s, k}^ \pm $和角偏中子流$J_{c, k}^ \pm $；Π_s^±和Π_c^±分别表示相应偏中子流方程c_i量的系数矩阵；E_ss^±、E_sc^±、E_cs^±、和E_cc^±分别表示相应偏中子流方程a_{s, k}和a_{c, k}量的系数矩阵。A_s、A_c通过式(20)的解析逆矩阵和给定的偏中子流$J_s^ - $、$J_c^ - $以及系数C共同确定。因此，在式(20)中消去矢量A_s、A_c，流出偏中子流$J_s^{\rm{ + }}$、$J_c^{\rm{ + }}$能够依据流入偏中子流$J_s^ - $、$J_c^-$以及系数C多项式展开：

$ \begin{array}{*{20}{l}} {J_s^ + = {H_s}C + {M_{ss}}J_s^ - + {M_{sc}}J_c^ - }\\ {J_c^ + = {H_c}C + {M_{cs}}J_s^ - + {M_{cc}}J_c^ - } \end{array} $

(21)

式中：${H_s}$、${H_c}$分别表示相应流出偏中子流方程c_i量的系数矩阵；${M_{ss}}$、${M_{sc}}$、${M_{cs}}$和${M_{cc}}$分别表示相应流出偏中子流方程$J_s^ - $和$J_c^ - $量的系数矩阵。

1.3.2 轴向积分

在整个六边形上积分式(9)，可得沿z轴方向径向平均通量$\mathit{\bar \Phi} \left({z, t} \right)$的一维方程：

$ - {D_g}\left( t \right)\frac{{{d^2}}}{{d{z^2}}}{\mathit{\bar \Phi} _g}\left( {z, t} \right) + {\mathit{\tilde \Sigma} _g}\left( t \right){\overline {\mathit{\tilde \Phi}} _g}\left( {z, t} \right) = {\bar Q_g}\left( {z, t} \right) $

(22)

其中：

$ {\bar Q_g}\left( {z, t} \right) = {\bar S_g}\left( {z, t} \right) - {\bar L_g}\left( {z, t} \right) $

(23)

式中：${\mathit{\bar \Phi} _g}\left({z, t} \right)$为平均通量；${\bar S_g}\left({z, t} \right)$为源项和${\bar L_g}\left({z, t} \right)$为径向积分泄漏项。

采用类似于上面二维平面的求解方法，求解在轴向（${z_0} = {z_i} - \frac{{{a_z}}}{2}$和${z_0} = {z_i}{\rm{ + }}\frac{{{a_z}}}{2}$间）方程。通量$\mathit{\Phi} \left({z, t} \right)$采用二阶多项式和指数函数展开。类似地，定义以下变量：

$ \begin{array}{l} z'' = \frac{z}{{{a_z}}}, D'' = \frac{D}{{{a_z}}}, \mathit{\Sigma} '' = \mathit{\Sigma} \cdot {a_z}, \\ \bar S'' = \bar S \cdot {a_z}, \bar L'' = \bar L \cdot {a_z}, \bar Q'' = \bar Q \cdot {a_z} \end{array} $

(24)

通量展开^[8]：

$ \begin{array}{c} \mathit{\hat \Phi} \left( {z'', t} \right) = \sum\limits_{i = 1}^2 {c_i^z\left( t \right){f_i}\left( {z'', t} \right)} + \\ \;a_1^z\left( t \right)\exp \left( {B''z''} \right) + a_2^z\left( t \right)\exp \left( { - B''z''} \right) \end{array} $

(25)

其中：$B'' = \sqrt {\frac{{\mathit{\Sigma} ''}}{{D''}}} $，展开多项式为：

$ \begin{array}{l} {f_0}\left( {z''} \right) = 1\\ {f_1}\left( {z''} \right) = 2\sqrt 3 z''\\ {f_2}\left( {z''} \right) = \sqrt 5 \left( {\frac{1}{2} - 6{{z''}^2}} \right) \end{array} $

(26)

函数${f_i}\left({z''} \right)$也满足正交性关系。

缓发中子先驱核${\bar C_j}\left({z'', t} \right)$多项式展开表示为：

$ {\bar C_j}\left( {z'', t} \right) \approx \sum\limits_{i = 0}^2 {c_{{\rm{pre}}, j, i}^z\left( t \right) \cdot {f_i}\left( {z''} \right)} $

(27)

径向积分泄漏项$\bar L\left({z'', t} \right)$通过多项式逼近：

$ \bar L\left( {z'', t} \right) \approx \sum\limits_{i = 0}^2 {l_i^z\left( t \right){f_i}\left( {z''} \right)} $

(28)

将式(25)、(27)和(28)展开带入式(22)，获得高阶展开系数方程：

$ \begin{array}{l} \left( {\mathit{\Sigma} _r^n\left( t \right) + \frac{{{\mathit{\Theta} ^n}}}{{v_1^{}}}} \right)c_{1, i}^{z, n}\left( t \right) = \\ \quad \frac{1}{{{k_{{\rm{eff}}}}}}\sum\limits_{g = 1}^2 {\left( {1-\sum\limits_{j = 1}^M {\beta _{g, j}^n\eta _j^n} } \right)\nu \mathit{\Sigma} _{f, g}^n(t)c_{g, i}^{z, n}\left( t \right)} {\rm{ + }}\\ \quad \sum\limits_{j = 1}^M {\lambda _j^nc_{{\rm{pre}}, j, i}^{z, n}\left( {t-\Delta t} \right)\exp \left( {-\lambda _j^n\Delta t} \right)} - l_{1, i}^{z, n}\left( t \right)\\ \quad \left( {\mathit{\Sigma} _a^n\left( t \right) + \frac{{{\mathit{\Theta} ^n}\Delta t}}{{v_2^{}}}} \right)c_{2, i}^{z, n}\left( t \right) = \mathit{\Sigma} _s^n(t)c_{1, i}^{z, n}\left( t \right) - l_{2, i}^{z, n}\left( t \right) \end{array} $

(29)

采用类似二维情况下的处理方法，可以获得在节块的底部(z₀)和顶部(z₁)的流出偏中子流J_z₀⁺、J_z₁⁺和流入偏中子流J_z₀^-、J_z₁^-表达式：

$ J_z^ \pm = {\mathit{\Pi} ^{z \pm }}{C^z} + {{ E}^{z \pm }}{A^z} $

(30)

式中：Π^z±表示相应偏中子流方程c_i^z量的系数矩阵；E^±表示相应偏中子流方程$a_1^z$和$a_2^z$量的系数矩阵。通过此表达式可以获得展开式中的系数$a_1^z、a_2^z$。在此矩阵方程中消去$a_1^z$和$a_2^z$，轴向流出偏中子流可以通过流入偏中子流表示为：

$ J_z^ + = {{ H}^z}{C^z} + {{ M}^z}J_z^- $

(31)

式中：${H^z}$表示相应流出偏中子流方程$c_i^z$量的系数矩阵；${M^z}$表示相应流出偏中子流方程$J_z^ - $量的系数矩阵。

式(21)和(31)共同构成了一个三维问题的内迭代过程。裂变、散射和泄漏项系数在外迭代步进行更新。

1.4 边界条件

假设偏中子流在系统外部边界处使用Albedo边界条件，在系统的所有外部面i的边界条件两能群表示为：

$ \begin{array}{l} J_{s, i, 1}^ - = { K}_{11}^sJ_{s, i, 1}^ + \\ J_{s, i, 2}^ - = { K}_{21}^sJ_{s, i, 1}^ + + { K}_{22}^s J_{s, i, 2}^ + \end{array} $

(32)

式中：Albedo系数${K}_{gg'}^s$作为输入参数。在式(32)中，第二个关系式的右手边的第一项表示快中子慢化后流入热中子。

真空边界条件：

$ { K}_{21}^s{\rm{ = }}0, { K}_{gg}^s \cong 0 $

(33)

零通量边界条件：

$ {\boldsymbol{ K}}_{21}^s = 0, {\boldsymbol{ K}}_{gg}^s = - 1 $

(34)

1.5 动态反应性模型

将时间相关的中子通量分布$\mathit{\Phi} _g^n\left({r, t} \right)$表示为空间、能群和时间相关的形状函数$\mathit{\Psi} _g^n\left({r, t} \right)$和幅函数$N\left(t \right)$的乘积：

$ \mathit{\Phi} _g^n\left( {r, t} \right) = N\left( t \right) \cdot \mathit{\Psi} _g^n\left( {r, t} \right) $

(35)

参考Henry的推导过程^[9]，可得动态反应性$\rho \left(t \right)$表示为：

$ \begin{array}{l} \rho \left( t \right) = \\ {\left[{\sum\limits_n {\int\limits_{{V_n}} {{\rm{d}}VW_1^n\left( r \right)\sum\limits_{g' = 1}^2 {\nu \mathit{\Sigma} _{f, g'}^n\left( t \right)\mathit{\Psi} _{g'}^n\left( {r, t} \right)} } } } \right]^{ - 1}} \cdot \\ \left[{\sum\limits_{g = 1}^2 {\sum\limits_n {\int\limits_{{V_n}} {{\rm{d}}V \cdot W_g^n\left( r \right)\left\{ {\nabla D_g^n\left( t \right)\nabla \mathit{\Psi} _g^n\left( {r, t} \right)} \right\}} } } } \right.-\\ \left. {\sum\limits_n {\int\limits_{{V_n}} {{\rm{d}}V\left\{ {\sum\limits_{g = 1}^2 {W_g^n\left( r \right)\mathit{\Sigma} _g^n\left( t \right)\mathit{\Psi} _g^n\left( {r, t} \right)} } \right\}} } } \right] -\\ W_1^n\left( r \right)\sum\limits_{g' = 1}^2 {\nu \mathit{\Sigma} _{f, g'}^n\left( t \right)\mathit{\Psi} _{g'}^n\left( {r, t} \right)} -W_2^n\left( r \right)\mathit{\Sigma} _s^n\left( t \right)\mathit{\Psi} _1^n\left( {r, t} \right) \end{array} $

(36)

式中：$W_g^n\left(r \right)$表示权重函数，这里选取共轭通量作为权重函数。

1.6 控制棒尖端效应处理模型

为了消除控制棒尖齿效应，国内外提出了各种相应的修正方法^[10-11]，本文采用如下通量密度权重来求均匀化截面：

$ {\mathit{\Sigma}_{{\rm{flux}}}} = \frac{{{\mathit{\Sigma}_{{\rm{CR}}}} \cdot {\mathit{\Phi} _{{\rm{CR}}}} \cdot {V_{{\rm{CR}}}} + {\mathit{\Sigma}_{{\rm{noCR}}}} \cdot {\mathit{\Phi} _{{\rm{noCR}}}} \cdot {V_{{\rm{noCR}}}}}}{{{\mathit{\Phi} _{{\rm{CR}}}} \cdot {V_{{\rm{CR}}}} + {\mathit{\Phi} _{{\rm{noCR}}}} \cdot {V_{{\rm{noCR}}}}}} $

(37)

式中：Σ_CR和Σ_noCR分别表示控制棒完全插入和未插入时节块相应的核截面；${\mathit{\Phi} _{{\rm{CR}}}}$和${\mathit{\Phi} _{{\rm{noCR}}}}$分别表示控制棒完全插入和未插入时相应的节块通量密度，这里作为权重因子。

1.7 截面模型

均匀化两群中子数据（权重中子通量、平均节块中子扩散系数、截面、组件不连因子、中子毒物相关参数和缓发中子相关参数）采用栅元组件程序CASMO-4^[12]生成，按照一定格式编辑，制作成相应的核数据库，作为程序的输入参数。核数据库必须包含与燃料单元类型、富集度和有无可燃吸收体对应的两群中子数据以及堆芯反射层核数据。如果堆芯有控制棒，数据库包含考虑控制棒的堆芯均匀化中子数据。

通过栅元/组件程序计算在不同燃耗、燃料密度、燃料温度和慢化剂温度(${b_l}、{\rho _{F, l}}、{T_M}、{T_{F, l}}$)的一系列点数据。在堆芯中子动力学程序中，堆芯节块求解中子方程需要实际参数(${b_l}、{\rho _{F, l}}、{T_M}、{T_{F, l}}$)对应的核数据。因此，通过基于一系列点数据的线性插值获得实际计算所需中子参数。

实际的截面、扩散系数和其它的中子参数可以统一表示为以下形式：

$ \begin{array}{*{20}{l}} {\mathit{\Sigma }\left( {b, {\rho _F}, {T_F}, {T_M}} \right) = {\mathit{\Sigma }_{{\rm{base}}}}\left( b \right) + \Delta {\mathit{\Sigma }_{{\rho _F}}}\left( b \right) + }\\ {\quad \Delta {\mathit{\Sigma }_{\sqrt {{T_F}} }}\left( b \right) + \Delta {\mathit{\Sigma }_{{T_M}}}\left( b \right) + \Delta {\mathit{\Sigma }_{{\rm{CR}}}}\left( {b, {\rho _F}} \right)} \end{array} $

(38)

式中：Σ_base(b)表示在正常运行参数和实际燃耗b情况下的基本截面。后面三项分别表示实际热工水力条件下的修正，最后一项是有关控制棒的修正。

程序通过线性插值数据集的第一组核数据，计算实际燃耗b下的基本截面Σ_base(b)。实际燃耗不能超过数据库中提供的最大燃耗，否则，程序将停止运行；式(38)中的剩余项采用基于核数据库的样条插值方法计算。

2 数值验证

根据以上理论模型，开发了三维六角形节块瞬态分析程序TCORE3D-HEX。为了检验算法和程序的正确性，使用程序对VVER无反馈弹棒事故和简单的绝热多普勒反馈弹棒事故两个三维瞬态国际基准题算例进行了计算，并将结果和相应的KIKO3D^[13]、DYN3D^[14]和HEXTRAN^[15]程序计算结果进行了比较。

2.1 基准题1

基准题1^[16]主要模拟VVER类型堆在初始功率接近零的情况下，发生无反馈弹棒事故。VVER类型堆堆芯水平布置的1/2结构图如图 3所示，纵向布置如图 4所示。

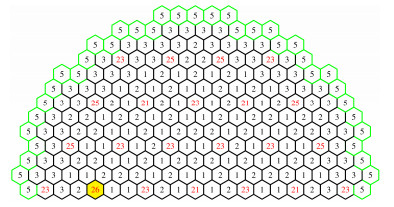
图 3 基准题1 VVER 1/2堆芯水平布置（26号为弹出控制棒） Figure 3 Horizontal map of half reactor in 3D hexagonal benchmarks (the ejected rod is marked with No.26)

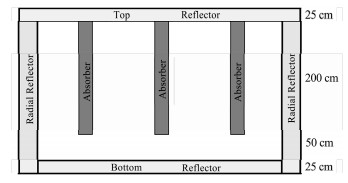
图 4 基准题1 VVER初始时刻堆芯纵向布置 Figure 4 Initial vertical cross section of the reactor in 3D hexagonal benchmarks

瞬态过程：初始时刻，23和25号安全棒位于堆芯外，而26和21号控制棒则位于底部反射层上方50 cm处；从0 s开始，26号控制棒从初始位置开始匀速弹出，0.08s后完全弹出堆芯；在1 s时，23和25号安全棒开始匀速下落，11s后完全到达堆芯底部，其中21号控制棒也在1s时开始以相同的速度匀速下落。基准题1详细描述请参考文献[16]。

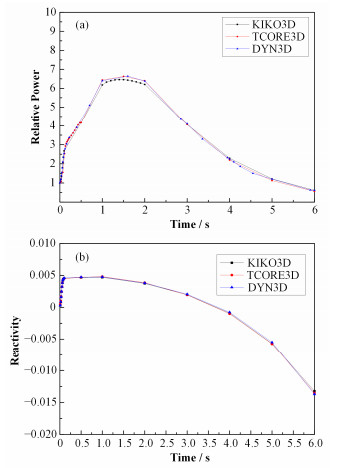
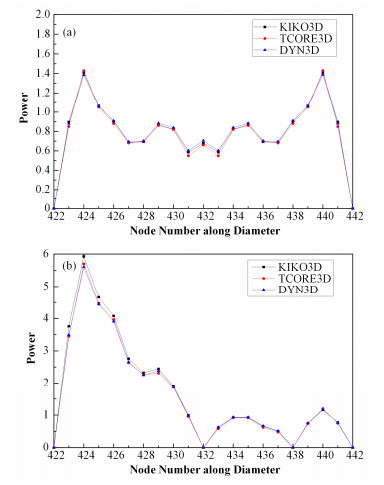
图 5给出了TCORE3D-HEX计算得到功率和反应性随时间变化与文献[16]中给出结果的比较，结果符合很好。图 6为0s时轴向第三层沿弹出棒所在直径方向的径向功率分布各程序的计算结果比较和6.0s时该位置的径向功率分布各程序的计算结果比较，如图 6所示，TCORE3D-HEX与参考程序的计算结果都符合得很好。

图 5 相对功率(a)和反应性(b)随时间变化 Figure 5 Behavior of normalized total power (a) and reactivity (b) during the transient

图 6 t=0 s (a)和t=6.0s (b)时轴向第三次(K=3)径向功率分布 Figure 6 Normalized radial power distribution at t=0 s (a) and t=6.0s (b) in No.3 axial plane

2.2 基准题2

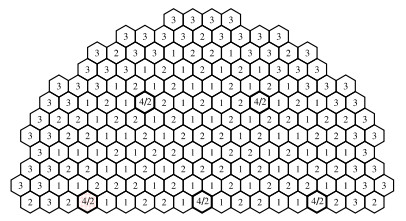
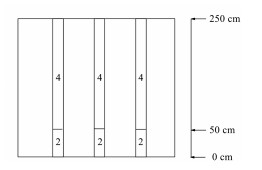
基准题2^[17]模拟VVER类型堆带有绝热条件的多普勒反馈机制弹棒事故。基准题2 VVER类型堆芯水平布置的1/2结构图如图 7所示，初始时刻纵向布置如图 8所示。其中材料1、2和3表示燃料，材料4表示吸收材料。控制棒组件轴向由两种材料组成：上部是材料4，下部是材料2。因此，图 7中4/2表示控制棒，其中横线填充的控制棒组件表示异常控制棒组K6。基准题2详细描述请参考文献[17]。

图 7 基准题2 VVER堆芯1/2水平布置 Figure 7 Core map with the fuel types

图 8 基准题2 VVER堆芯初始时刻纵向布置 Figure 8 Axial scheme of core along the lowest row of core map

瞬态过程：初始时刻，控制棒全部插入堆芯，堆芯处于热态零功率(Hot Zero Power, HZP)，初始功率1.375kW。在0.16s时，K6控制棒以恒定的12.5m·s^-1速度发生弹棒。反馈机制主要基于燃料温度绝热增加（初始燃料温度260℃）。瞬态模拟过程持续2s。

表 1给出了TCORE3D-HEX计算的初始有效增殖因子、弹棒后的有效增殖因子和弹出棒的静态反应性与文献[17]中给出结果的比较。表 2给出了TCORE3D-HEX计算的不同时刻的功率峰因子与参考文献[17]中给出结果的比较。表 1、2数据表明：TCORE3D-HEX与DYN3D、KIKO3D和HEXTRAN程序计算结果都符合得很好。

表 1 初始有效增殖因子(k_{eff, 0})、弹棒后的有效增殖因子(k_{eff, 1})以及弹出棒的静态反应性(ρ) Table 1 Static eigenvalue in the initial state (k_{eff, 0}), in the state with ejected rod (k_{eff, 1}) and static reactivity worth of the ejected rod

表 2 不同时刻的功率峰因子 Table 2 Power peaking factors at different time points

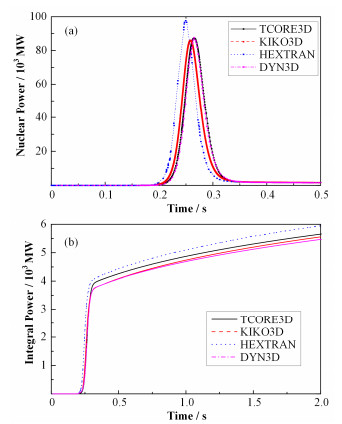
图 9给出了TCORE3D-HEX计算得到功率和总的释热随时间变化与文献[17]给出结果的比较，如图 9所示，结果符合良好。但是，由于不同程序计算过程中引入的最大反应性不同（表 1），更高的反应性引入导致更高和更早的功率峰值。不同的功率峰值导致不同的总释热。

图 9 功率(a)和总释热(b)随时间变化 Figure 9 Nuclear power (a) and integral power (b) vs. time

3 结语

目前，各国正积极开展熔盐堆概念和工程设计，其中瞬态分析和安全评估是一项重要内容。节块展开法具有计算速度快、能给出高精度的节块平均通量的优点，广泛应用于反应堆多维动力学计算。指数变换方法能够减少中子通量离散过程中的截断误差，减少计算引入的系统误差，能够满足反应堆物理提出的新的“高保真”要求。同时，熔盐冷却固态燃料熔盐堆广泛地采用六角形棱柱组件。因此，基于指数变换和六角形节块展开法，开发了熔盐堆三维时空动力学程序TCORE3D-HEX，并通过对无反馈弹棒事故和简单的绝热多普勒反馈弹棒事故两个VVER国际瞬态基准题算例的验算，初步验证了程序的正确性。TCORE3D-HEX程序能够应用于六角形组件熔盐冷却固态燃料熔盐堆各种动力学瞬态分析，为TMSR熔盐冷却先进高温堆瞬态分析和安全评估提供了可靠的分析和评估工具。

参考文献

[1]	OECD NEA. Technology roadmap update for generation Ⅳ nuclear energy systems[EB/OL]. [2017-12-04]. https://www.gen-4.org/gif/upload/docs/application/pdf/2014-03/gif-tru2014.pdf.
[2]	Ingersoll D T, Forsberg C W, Ott L J, et al. Status of preconceptual design of the advanced high-temperature reactor (AHTR)[R]. ORNL/TM-2004/104. USA: Oak Ridge National Laboratory, 2004.
[3]	Qualls A, Betzler B, Brown N, et al. Preliminary demonstration reactor point design for the fluoride salt-cooled high-temperature reactor[R]. ORNL/TM-2015/700. USA: Oak Ridge National Laboratory, 2015.
[4]	Qualls A, Brown N, Betzler B, et al. Fluoride salt-cooled high-temperature demonstration reactor point design[R]. ORNL/TM-2016/85. USA: Oak Ridge National Laboratory, 2016.
[5]	江绵恒, 徐洪杰, 戴志敏. 未来先进核裂变能—TMSR核能系统[J]. 中国科学院院刊, 2012, 27(3): 366-374. JIANG Mianheng, XU Hongjie, DAI Zhimin. Advanced fission energy program-TMSR nuclear energy system[J]. Bulletin of Chinese Academy of Sciences, 2012, 27(3): 366-374. DOI:10.3969/j.issn.1000-3045.2012.03.016
[6]	胡永明. 反应堆物理数值计算方法[M]. 长沙: 国防科技大学出版社, 2000.
[7]	Křepel J, Rohde U, Grundmann U, et al. DYN3D-MSR spatial dynamics code for molten salt reactors[J]. Annals of Nuclear Energy, 2007, 34: 449-462. DOI:10.1016/j.anucene.2006.12.011
[8]	Christoskov I, Petkov P T. A development of the HEXNEM nodal expansion method[J]. Annals of Nuclear Energy, 2013, 51: 235-239. DOI:10.1016/j.anucene.2012.06.036
[9]	Ott K O, Neuhold R J. Introductory nuclear reactor dynamics[M]. USA: American Nuclear Society, 1985.
[10]	Gehin J C. A quasi-static polynomial nodal method for nuclear reactor analysis[D]. Massachusetts Institute of Technology, 1992.
[11]	NESTLE version 5. 2. 1 manual[R]. USA: North Carolina State University Electric Power Research Center, 2003.
[12]	CASMO-4. A fuel assembly burnup program, methodology (SOA-95/2)[R]. Sweden: Studsvik, 1995.
[13]	Keresztúri A, Hegyi G, Marázcy C, et al. Development and validation of the three-dimensional dynamic code-KIKO3D[J]. Annals of Nuclear Energy, 2003, 30(1): 93-120. DOI:10.1016/S0306-4549(02)00043-9
[14]	Grundmann U, Rohde U. DYN3D/M2 a code for calculation of reactivity transients in cores with hexagonal geometry[R]. Report ZfK-690. Germany: HelmholtzZentrum Dresden-Rossendorf, 1989.
[15]	Kyrki-Rajamaki R. HEXTRAN: WER reactor dynamics code for three-dimensional transients[C]. Proceedings of the 1st Symposium of AER, KFKI/AEKI Atomenergia Press, 1991: 474-481.
[16]	Keresztúri A, Telbisz M. AER benchmark specification sheet: AER-DYN-001[R]. Germany: Institute of Safety Research, 2000.
[17]	Grundmann U, Rossendorf F Z. AER benchmark specification sheet: AER-DYN-002[R]. Germany: Institute of Safety Research, 1999.