2. 中国科学院核辐射与核能技术重点实验室 上海 201800;
3. 中国科学院大学 北京 100049
2. Key Laboratory of Nuclear Radiation and Nuclear Energy Technology, Chinese Academy of Sciences, Shanghai 201800, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China
熔盐堆是第四代反应堆核能系统的6种候选堆型之一[1],适合于钍铀燃料循环的开发,而配置了在线干法处理流程的熔盐堆核能系统有可能实现完全的钍铀燃料闭式循环[2]。干法处理是在高温、无水状态下处理辐照核燃料的化学工艺,具有耐辐照、低临界风险、放射性废物少等优点,适宜处理高燃耗、短冷却期的乏燃料,有望满足熔盐堆核能系统对燃料处理的需要[3]。其中氟化挥发法是利用U、Pu的氟化物与裂变产物的挥发性不同来实现目标元素分离的干法技术,分离过程简单,熔盐堆燃料盐的氟化挥发工艺需要在液态氟化物熔盐中通入氟气,其最主要技术难点是:高温氟化物熔盐和氟气有强腐蚀性,对设备材料腐蚀严重。为实现氟化反应器在如此强腐蚀环境下长时间安全、稳定的运行,冷冻壁技术被认为是一种有效的解决方案。所谓冷冻壁技术,即通过在容器外壁设置冷却换热措施,降低壁面温度,使高温熔体在内壁形成冷冻介质保护层,从而避免反应介质与容器内壁的接触,达到减轻材质腐蚀[4-5]的目的。
冷冻壁技术的关键点包括:冷冻壁形成与维持、冷冻壁厚度控制与测量、反应器内温度场监测。前期在硝酸盐体系下开展了冷冻壁形成与厚度测量的相关研究[6-8],主要采用外壁冷却的方式,掌握了冷冻壁形成工艺及测厚技术。本研究基于中心冷却式冷冻壁实验装置,在FLiNaK熔盐体系下开展了冷冻壁维持工艺研究,并为冷冻壁防护实验提供前期准备。在中心冷棒空气冷却下对比了不同釜体壁温对冷冻壁厚度和釜内温度场的影响,获得不同冷冻壁厚度的维持工艺条件。通过数值模拟的方法构建了适用于预测氟盐体系下冷冻壁厚度和温度场的计算模型,为后续的熔盐冷冻壁氟化反应器的设计及应用提供参考。
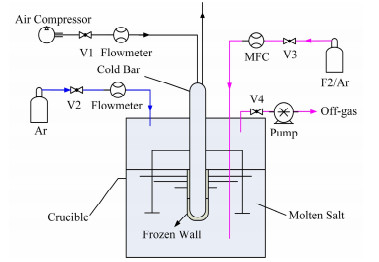
1 实验装置及实验步骤 1.1 实验装置中心冷却式冷冻壁实验装置如图 1所示。熔盐介质:FLiNaK熔盐(LiF-NaF-KF摩尔比:46.5%- 11.5%-42%),其熔点454 ℃。反应釜内径158mm,高度244mm。熔盐装载量约3.5kg,熔盐液位高度约110 mm。冷棒结构:中心冷棒通入压缩空气进行冷却,在冷棒周围形成冷冻壁,可实现在密封情况下,冷棒在釜内自由上下升降。冷棒周围布置了6个热电偶(精度0.1℃),用以测量反应釜内的温度场分布及监测冷冻壁厚度。气路及控制:中心冷却的空气回路有相应的阀门和流量计控制和监测空气流量。反应釜内熔盐液面上部空间通入Ar覆盖气,熔盐探底管内通入氟气。加热控温:加热炉额定功率3kW,加热上限温度800℃,可设置恒温控制模式,保持反应釜壁温维持在设定值。
|
图 1 实验装置简介 Figure 1 Schematic of experimental apparatus |
将小型块状的FLiNaK熔盐约3.5kg放置在反应釜内,密封法兰后,通入覆盖气Ar,通过循序加热程序将熔盐加热熔化,熔盐液位控制在110mm左右。
1.2.2 冷冻壁形成及维持待熔盐熔化后,通过升降装置控制冷棒下降至液相熔盐中,通过温控系统设置反应釜壁温,维持在恒定温度。开启空气压缩机,调节阀门,控制空气流量为恒定值,通过冷棒中心空气的冷却作用,在冷棒周围形成一定厚度的冷冻壁,可通过实时热电偶温度场变化监测冷冻壁厚度变化,6个热电偶距离冷棒的距离依次为0mm、0mm、5mm、10mm、20mm、30mm,如图 2所示。

|
图 2 热电偶位置分布 Figure 2 Distribution of the thermocouple |
待整体系统达到传热平衡时(径向热电偶温度恒定),可通过升降装置将冷棒提升脱离熔盐液面。并待熔盐自然冷却后,可观察和测量冷冻壁厚度。
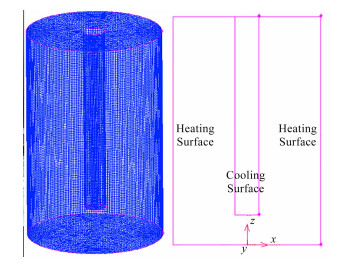
2 数值模拟计算模型物理模型:基于Fluent软件建立相应模型,如图 3所示。其中冷棒的直径为25mm,釜体直径为158mm,釜体高度为244mm。
|
图 3 模型简介 Figure 3 Schematic of the mode |
数学模型:控制方程参考文献[9],其中连续性方程如下:
| $ \frac{{\partial \left( {\rho u} \right)}}{{\partial x}} + \frac{{\partial \left( {\rho \upsilon } \right)}}{{\partial y}} = 0 $ | (1) |
式中:ρ为熔盐密度;u、υ分别为x、y轴速度。x和y轴方向的动量方程分别如下:
| $ \begin{array}{l} \frac{{\partial \left( {\rho u} \right)}}{{\partial \tau }} + \frac{{\partial \left( {\rho uu} \right)}}{{\partial x}} + \frac{{\partial \left( {\rho u\upsilon } \right)}}{{\partial y}}\\ \, \quad = - \frac{{\partial P}}{{\partial x}} + \frac{\partial }{{\partial x}}\left( {\mu \frac{{\partial u}}{{\partial x}}} \right) + \frac{\partial }{{\partial y}}\left( {\mu \frac{{\partial u}}{{\partial y}}} \right) + {S_x} \end{array} $ | (2) |
| $ \begin{array}{l} \frac{{\partial \left( {\rho \upsilon } \right)}}{{\partial \tau }} + \frac{{\partial \left( {\rho u\upsilon } \right)}}{{\partial x}} + \frac{{\partial \left( {\rho \upsilon \upsilon } \right)}}{{\partial y}}\\ = - \frac{{\partial P}}{{\partial y}} + \frac{\partial }{{\partial x}}\left( {\mu \frac{{\partial \upsilon }}{{\partial x}}} \right) + \frac{\partial }{{\partial y}}\left( {\mu \frac{{\partial \upsilon }}{{\partial y}}} \right) + \rho g\beta (T - {T_{\rm{m}}}) + {S_y} \end{array} $ | (3) |
式中:τ为时间;μ为熔盐动力粘度;P为压力;β为热膨胀系数;Tm为熔盐熔点;Sx和Sy为动量消耗项。
| $ {S_x} = - \frac{{{{\left( {1 - {f_{\rm{L}}}} \right)}^2}}}{{{f_{\rm{L}}}^3 + \varepsilon }}{A_{\rm{m}}}\left( {u - {u_p}} \right) $ | (4) |
| $ {S_y} = - \frac{{{{\left( {1 - {f_{\rm{L}}}} \right)}^2}}}{{{f_{\rm{L}}}^3 + \varepsilon }}{A_{\rm{m}}}\left( {\upsilon - {\upsilon _p}} \right) $ | (5) |
式中:Am为糊状区常数,为2.5×106;fL为熔盐液相体积分数,主要由熔盐温度决定。
| $ \begin{array}{l} {f_{\rm{L}}} = 0\begin{array}{*{20}{c}} {}&{{\rm{(}}\begin{array}{*{20}{c}} {T < {T_{\rm{s}}})}&{} \end{array}} \end{array}\\ {f_{\rm{L}}} = 1\begin{array}{*{20}{c}} {}&{(\begin{array}{*{20}{c}} {T > {T_{\rm{l}}})}&{} \end{array}} \end{array}\\ {f_{\rm{L}}} = \frac{{T-{T_{\rm{s}}}}}{{{T_{\rm{l}}}-{T_{\rm{s}}}}}\begin{array}{*{20}{c}} {}&{(\begin{array}{*{20}{c}} {{T_{\rm{s}}} < T < {T_{\rm{l}}})}&{} \end{array}} \end{array} \end{array} $ | (6) |
式中:Ts和Tl分别为熔盐固相温度和熔盐液相温度。
能量方程如下:
| $ \begin{array}{l} \frac{{\partial \left( {\rho H} \right)}}{{\partial \tau }} + \frac{{\partial \left( {\rho uH} \right)}}{{\partial x}} + \frac{{\partial \left( {\rho \upsilon H} \right)}}{{\partial y}}\\ \quad = \frac{\partial }{{\partial x}}\left( {k\frac{{\partial T}}{{\partial x}}} \right) + \frac{\partial }{{\partial y}}\left( {k\frac{{\partial T}}{{\partial y}}} \right) \end{array} $ | (7) |
式中:k为熔盐的导热系数;H为熔盐的焓。FLiNaK熔盐的相关物性可参考文献[10]进行计算。
参数设置:选择3D(压力基)稳态求解器,采用Solidification & Melting模型,釜壁及釜底为加热面,可根据加热器的恒温加热模式设置加热面为恒温边界条件。与熔盐接触的冷棒边界面为冷却界面,冷却面的对流换热系数为10.0W·m-2·k-1。在求解器控制参数的设置面板中设定压力和速度的耦合采用SIMPLE算法。
3 结果分析与讨论为研究不同实验条件对冷冻壁维持工艺的影响。主要对比了釜体壁温480~550℃范围内冷冻壁平衡厚度变化情况,实验结果如表 1所示。
| 表 1 冷冻壁实验结果对比 Table 1 Comparison of experimental results of frozen wall |
图 4为几组工况对应的冷冻壁实验照片。实验中空气冷却气来自于空气压缩机,进气温度略有差异,根据数据分析得出以下结论:冷冻壁厚度主要与釜体壁温有关。釜体壁温越高,冷冻壁厚度越小,当釜体壁温较低时,冷冻壁厚度较大,液相熔盐体积较小不利于氟化挥发工艺的开展;当釜体壁温高于550℃时,冷冻壁无法维持,无法对相关设备进行防护。

|
图 4 冷冻壁照片 Figure 4 Picture of the frozen wall |
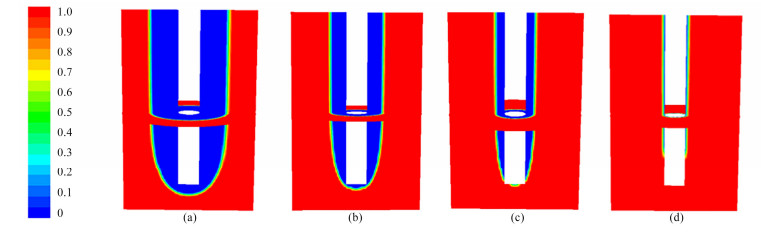
为建立一个有效、实用的冷冻壁及温度场预测模型,基于计算机流体力学(Computational Fluid Dynamics, CFD)软件获得了数值模拟计算结果,并与实验值进行了对比分析。图 5为不同工况下达到传热平衡后冷冻壁厚度分布情况,中心区域表示固相冷冻壁,外围区域表示液相熔盐。以工况(1)为例:中心冷却气体28℃、釜壁面温度480℃工况下模拟计算得到的冷冻壁厚度分布情况,冷冻壁径向平均厚度28.4mm,实验值24.7mm,与实验值较为吻合。表 1中列举了不同工况下冷冻壁厚度计算值与实验值的对比情况。通过对比结果来看,冷冻壁厚度模拟计算值与实验值较为吻合,能较为合理地预测传热平衡下冷冻壁的厚度分布情况。
|
图 5 熔盐液相体积分数(a)工况1,(b)工况2,(c)工况3,(d)工况4 Figure 5 Contours of molten salt liquid fraction (a) Condition 1, (b) Condition 2, (c) Condition 3, (d) Condition 4 |
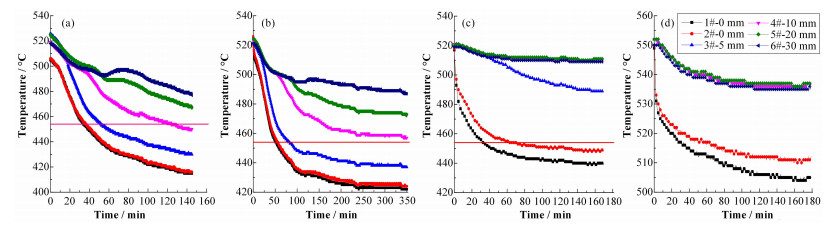
图 6为4个实验工况下釜内热电偶温度变化情况,在中心冷棒内通入空气后,釜内熔盐温度先急剧降低,当釜壁加热与冷棒冷却达到传热平衡后釜内温度场达到稳态,热电偶温度恒定。按热电偶径向位置分布和FLiNaK熔盐理论熔点454℃计算冷冻壁厚度,工况1~4下通过热电偶温度场计算得到的冷冻壁厚度分别为11.1mm、9.3mm、1.4mm、0mm,比实验值偏小。主要是由于处于固液交界面的热电偶有可能处于过渡区,温度略高于熔点,但提升样品架观察该热电偶仍处于冷冻壁内,因此冷冻壁实际测量值略有偏高。
|
图 6 热电偶温度变化(a)工况1,(b)工况2,(c)工况3,(d)工况4 Figure 6 Temperature of thermocouple (a) Condition 1, (b) Condition 2, (c) Condition 3, (d) Condition 4 |
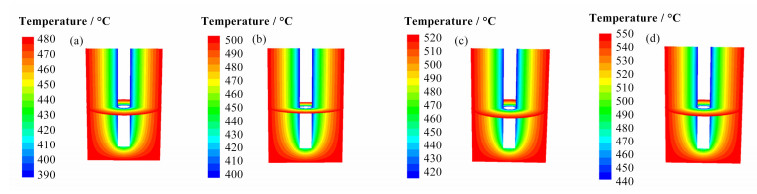
图 7分别为通过模拟计算得到的4个工况达到传热平衡时的温度场分布,表 2为4个工况下不同径向位置温度计算值与实验值对比情况,具体对比了距离冷棒表面0mm、5mm、10mm、20mm、30mm处温度对比,通过模拟计算得到的釜内温度场分布与实验值较为吻合,相关温度场分布能够为后续氟化挥发工艺提供参考。
|
图 7 温度场分布(a)工况1,(b)工况2,(c)工况3,(d)工况4 Figure 7 Distribution of temperature (a) Condition 1, (b) Condition 2, (c) Condition 3, (d) Condition 4 |
| 表 2 温度场计算值对比(℃) Table 2 Comparison of calculated values of temperature |
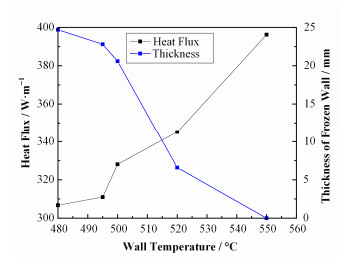
在实验中可通过空气侧的流量与进出口温差获得热流量信息,图 8为实验中不同工况下达到传热平衡后的热流量与釜体壁温的关系,随着釜体壁温的升高,热流量逐渐增大,冷冻壁厚度逐渐减小。并且达到550℃后,热流量显著增加,冷冻壁无法维持。因此也可通过热流量的相关信息指导冷冻壁的厚度调节和控制。
|
图 8 热流量与釜体壁温关系 Figure 8 Relationship between heat flux and wall temperature |
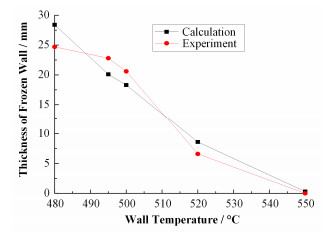
图 9为釜体壁温与冷冻壁厚度的关系,数值模拟计算值与实验值较为吻合,随着釜体壁温升高,冷冻壁厚度逐渐减小,在达到550℃时冷冻壁厚度无法维持。为保证冷冻壁维持在适宜的厚度范围内,可将壁温设置在500~520℃,冷冻壁厚度范围20.6~6.6mm。
|
图 9 釜体壁温与冷冻壁厚度关系 Figure 9 Relationship between wall temperature and frozen wall thickness |
基于中心冷却式冷冻壁实验装置,在FLiNaK熔盐体系下开展了中心冷棒气体冷却方式下冷冻壁的维持实验研究。实验获得在不同釜体壁温480~550℃情况下达到静态平衡后冷冻壁的厚度范围为24.7~0mm。釜体壁温500~520℃,冷冻壁厚度为20.6~6.6mm能够满足氟化反应的工艺要求。通过实验获得了热流量与釜体壁温的关系,随着釜体壁温的升高,热流量逐渐增大,冷冻壁厚度逐渐减小。并且达到550℃后,热流量显著增加,冷冻壁无法维持。
建立了数值模拟计算模型,计算了冷冻壁的传热平衡工况,分别得到了在不同釜体壁温下对应的冷冻壁厚度范围及温度场分布,与实验值比较能够较为准确地反映真实情况,能够应用于今后冷冻壁氟化挥发工艺中冷冻壁厚度和温度场的模拟预测。
| [1] |
Cheng M S, Dai Z M. Development of a three dimension multi-physics code for molten salt fast reactor[J]. Nuclear Science and Techniques, 2014, 25(1): 010601. DOI:10.13538/j.1001-8042/nst.25.010601 |
| [2] |
江绵恒, 徐洪杰, 戴志敏. 未来先进核裂变能-TMSR核能系统[J]. 中国科学院院刊, 2012, 27(3): 366-374. JIANG Mianheng, XU Hongjie, DAI Zhimin. Advanced fission energy program-TMSR nuclear energy system[J]. Bulletin of Chinese Academy of Sciences, 2012, 27(3): 366-374. DOI:10.3969/j.issn.1000-3045.2012.03.016 |
| [3] |
刘学刚. 乏燃料干法处理技术研究进展[J]. 核化学与放射化学, 2009, 31: 35-44. LIU Xuegang. Research on dry reprocessing technology of spent nuclear fuel[J]. Journal of Nuclear and Radiochemistry, 2009, 31: 35-44. |
| [4] |
Kessie R W, Gabor J D, Mecham W J, et al. Process vessel design for frozen-wall containment of fused salt (ANL-6377)[R]. USA: Argonne National Laboratory, 1961.
|
| [5] |
Whatley M E. Unit operations section quarterly progress report (ORNL-4365)[R]. USA: Oak Ridge National Laboratory, 1968.
|
| [6] |
周金豪, 孙波, 佘长锋, 等. 熔盐冷冻壁形成及控制实验研究[J]. 核技术, 2015, 38(7): 070602. ZHOU Jinhao, SUN Bo, SHE Changfeng, et al. Experimental research on the formation and controlling of molten salt frozen-wall[J]. Nuclear Techniques, 2015, 38(7): 070602. DOI:10.11889/j.0253-3219.2015.hjs.38.070602 |
| [7] |
周金豪, 孙波, 佘长锋, 等. 熔盐冷冻壁厚度测量方法[J]. 化工进展, 2016, 35(8): 2373-2380. ZHOU Jinhao, SUN Bo, SHE Changfeng, et al. Experimental study on the thickness detection of molten salt frozen-wall[J]. Chemical Industry and Engineering Progress, 2016, 35(8): 2373-2380. DOI:10.16085/j.issn.1000-6613.2016.08.11 |
| [8] |
孙波, 周金豪, 佘长锋, 等. 熔盐冷冻壁应用中关键工艺影响因素研究[J]. 核技术, 2016, 39(8): 080602. SUN Bo, ZHOU Jinhao, SHE Changfeng, et al. Experimental study on the influence of key factors in the application of molten salt frozen wall[J]. Nuclear Techniques, 2016, 39(8): 080602. DOI:10.11889/j.0253-3219.2016.hjs.39.080602 |
| [9] |
Tiari S, Qiu S G, Mahdavi M. Numerical study of finned heat pipe-assisted thermal energy storage system with high temperature phase change material[J]. Energy Conversion and Management, 2015, 89: 833-842. DOI:10.1016/j.enconman.2014.10.053 |
| [10] |
Ferng Y M, Lin K Y, Chi C W. CFD investigating thermal-hydraulic characteristics of FLiNaK salt as a heat exchange fluid[J]. Applied Thermal Engineering, 2012, 37: 235-240. DOI:10.1016/j.applthermaleng.2011.11.021 |


