2. 海军驻上海江南造船(集团)有限责任公司军事代表室 上海 201913
2. Naval Military Representative Department of Jiangnan Shipyard, Shanghai 201913, China
质子交换膜燃料电池(Proton Exchange Membrane Fuel Cell, PEMFC)是一种将氢气的化学能通过电化学反应直接转化为电能的装置。因其能量转换效率高、环境友好、可快速启动等特点,可成为交通运输以及固定电站的能量来源。PEMFC工作时,内部会有流体流动、电化学反应、质子传递、电子传导和温度传递等过程。由于电子的传导速度要快于其他过程,在大电流加载时,电池内的反应气体来不及传递,导致电池出现短暂“饥饿”现象,造成输出电压骤降至零甚至反极,严重影响电池寿命[1]。因此,理解燃料电池的动态特性有利于对燃料电池进行合理的设计与控制。
Hwang等[2]利用FLUENT软件建立了一个三维非等温单相流电池模型,模拟了负载电压从0.7 V突变至0.5 V的过程。在电压突变之后,可以明显地观察到电流密度出现上调现象,并在约0.3 s之后达到稳定。Kim等[3-4]保持进气量恒定条件下,实验研究了燃料电池流场、气体过量系数、反应物浓度以及电压突变的情况下,电流的响应情况。Hu等[5]建立了一个三维非等温单相流电池模型,研究了蛇形流道燃料电池的启动过程,阴极空气过量系数与湿度的阶跃变化与周期变化的过程。在模拟启动过程中,发现水从阳极到阴极的净通量大于氢气的消耗量,使得阳极的氢气浓度沿流道方向逐渐增加,并且氢气浓度达到稳定的时间比氧气浓度达到稳定的时间要长,主要是因为阴极的气体流速大于阳极的气体流速,对流传质占主要因素。Cho等[6-7]对燃料电池单元进行瞬态加载实验,研究了瞬时电流加载时,电池系统的响应时间与阴极的水淹情况。由于电流的加载,产生了更多的液态水,催化层发生局部“水淹”现象,造成反应物局部“饥饿”,从而达到稳定的时间会更长。增加阳极和阴极的气体过量系数,流道内的气体速度提高,使得生成的水更易排出,减轻了电池的水淹情况,有利于系统更快地达到稳定。比较两个催化层有效面积不同(25cm2和330 cm2)的燃料电池,电压下调现象受到氧气供给延迟、氧气浓度分布不均、阴极水淹以及膜内水平衡等多种因素的共同影响。在膜内水分充足时,系统更易达到稳定。本文通过对直通道质子交换膜燃料电池进行简化建模,选取合适的参数进行数值计算,比较不同电流密度加载时间以及加载幅度的情况下,燃料电池的电压和正负极气体浓度响应情况,进而研究燃料电池动态加载特性。
1 模型描述 1.1 模型假设本文使用ANSYS FLUENT软件进行数值计算,采用三维、单相、非等温的瞬态模型,模型所采用的假设如下:
1) 电化学反应生成的水以水蒸气的形式存在;
2) 流道内气体视为理想气体,且层流流动;
3) 气体扩散层(Gas Diffusion Layer, GDL)、催化层以及膜各向同性;
4) 反应气不能穿过膜。
1.2 数学描述主要的数学方程包括质量守恒、动量守恒、组分守恒、能量守恒以及电荷守恒方程。主要形式为:
1) 质量守恒方程:
| $ \frac{{\partial \left( {\varepsilon \rho } \right)}}{{\partial t}} + \nabla \cdot \left( {\varepsilon \rho \vec u} \right) = {S_{\rm{mass}}} $ | (1) |
2) 动量守恒方程:
| $ \frac{{\partial \left( {\varepsilon \rho \vec u} \right)}}{{\partial t}} + \nabla \cdot \left( {\varepsilon \rho \vec u\vec u} \right) =-\varepsilon \nabla p + \nabla \cdot \left( {\varepsilon \mu \nabla \vec u} \right) + {S_{\rm{mom}}} $ | (2) |
3) 组分守恒方程:
| $ \frac{{\partial \left( {\varepsilon \rho {c_i}} \right)}}{{\partial t}} + \nabla \cdot \left( {-\varepsilon \rho {D_i}\nabla {c_i}} \right) + \nabla \cdot \left( {\varepsilon \rho \overrightarrow u {c_i}} \right) = {S_i} $ | (3) |
4) 能量守恒方程:
| $ \frac{{\partial \left( {\varepsilon \rho {c_p}T} \right)}}{{\partial t}} + \nabla \cdot \left( {-\varepsilon \rho \lambda \nabla {c_p}T} \right) + \nabla \cdot \left( {\varepsilon \rho \overrightarrow u {c_p}T} \right) = {S_T} $ | (4) |
方程中各个参数的含义以及其他未列举出来的方程详见文献[5]。
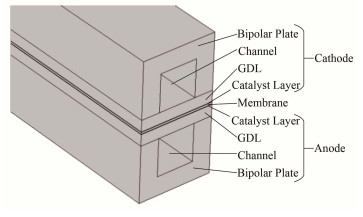
1.3 计算域及其边界条件计算域的三维模型如图 1所示,其几何参数见表 1。在数值模拟中,阴/阳极的入口和出口,膜与催化层的界面均采用第一类边界条件。固体壁面为无滑移边界条件。
|
图 1 几何模型 Figure 1 Geometric model |
| 表 1 几何参数 Table 1 Geometric parameters |
计算有关的几何参数和材料参数等见表 1和2。阳极和阴极流道内,流体流动的方向一致。
| 表 2 材料参数及操作参数 Table 2 Parameters of material and operating |
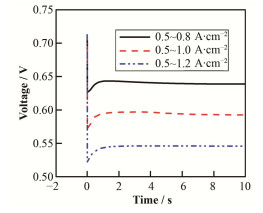
加载时间固定为0.01 s,加载幅度分别为0.5~0.8 A∙cm-2、0.5~1.0 A∙cm-2以及0.5~1.2 A∙cm-2。电压的变化情况如图 2所示。从图 2中可以看出,同样的加载时间内,加载幅度越大,电池电压的下调情况越严重。这是因为大电流加载时,消耗的反应气更多,由于电池内部的传质存在滞后现象,因此反应气不能及时到达催化层,使得催化层出现短暂的缺气情况,造成电压出现下调。同时,加载幅度越大,电池达到稳定的时间越长。
|
图 2 不同加载幅度下的电压响应曲线 Figure 2 Voltage response curves at different load |
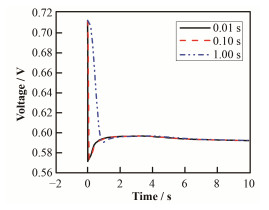
加载幅度固定为0.5~1.0 A∙cm-2,加载时间分别为0.01 s、0.1 s和1 s。电压的变化情况如图 3所示。加载时间分别为0.01 s、0.1 s时电压响应曲线变化幅度不明显,而加载时间为1 s时的曲线有明显区别。从图 3中可以看出,变载时间越短,电压下调越严重。这是因为在短的变载时间内,反应气的消耗会更快,导致电池内部暂时缺气更严重。当变载时间极小时,电压下调幅度差别呈减小趋势。这是因为在变载极小情况下,反应气消耗变化差异不再明显。
|
图 3 不同变载时间下的电压响应曲线 Figure 3 Voltage response curves at different transient time |
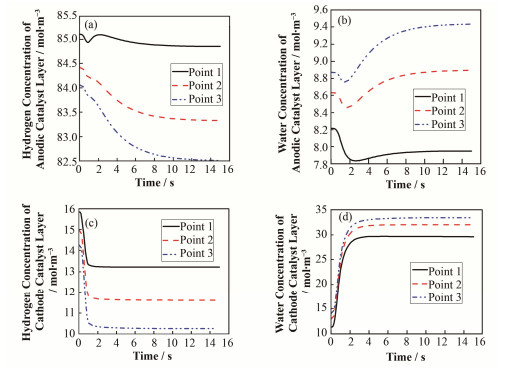
为了定性比较不同位置处反应气的响应特征,选取阴/阳催化层沿流道方向中间切面上的等距的3个点,具体点的分布如图 4所示。在加载幅度为0.5~1.0A∙cm-2、加载时间为1 s的情况下,催化层中的氢气浓度、氧气浓度、阴/阳极水浓度的变化情况分别如图 5所示。

|
图 4 催化层中间层的取点分布 Figure 4 Catalyst layer intermediate layer taking point distribution |
|
图 5 阳极(a、b)和阴极(c、d)催化层氢气浓度变化曲线和水浓度变化曲线 Figure 5 Curve of anodic (a, b) and cathode (c, d) catalyst layer hydrogen concentration and water concentration |
从图 5(a)可以看出,在1 s的加载时间内,受到传质速度的影响,阳极氢气快速消耗,并且来不及供应,使得在1 s的加载时间之后,氢气浓度依然逐渐降低。靠近出口处的氢气浓度达到稳定的时间要更长。图 5(a)中,开始阶段水的浓度降低,是因为随着加载电流的增加,电拖作用将阳极的水运到阴极,随后水的反向扩散作用占据优势,阴极侧的水扩散回阳极侧,因此出现了先降低后升高的变化情况。在阴极,电化学反应要比电拖作用和反扩散作用对水的影响更明显,因此,阴极水浓度的变化主要受电化学反应的影响,所以会出现阴极催化层水浓度逐渐升高的趋势,如图 5(b)所示。从图 5(b)中也可以看出,燃料电池加变载时,阴极达到稳定所需的时间要比阳极更短。
3 结语本文以合适的质子交换膜燃料电池单元模型作为数值模拟研究对象,通过合理假设和选取合适的参数,对比不同加载时间和加载幅度情况下,电压响应特性及两极反应气浓度变化情况。比较得出以下结论:
1) 加载时间一定时,降低加载幅度,有利于提高燃料电池的稳定性。
2) 加载幅度一定时,延长加载时间,燃料电池电压出现下调现象会得到缓解,有利于稳定性的提高,从而提高电池寿命。
3) 加载时,阴极比阳极达到稳定的时间要更短。
| [1] |
方源, 章桐. 质子交换膜燃料电池动态响应研究综述[J]. 电源技术, 2013, 137(10): 1875-1876. FANG Yuan, ZHANG Tong. Survey on dynamic response of proton exchange membrane fuel cell[J]. Chinese Journal of Power Sources, 2013, 137(10): 1875-1876. DOI:10.3969/j.issn.1002-087X.2013.10.055 |
| [2] |
Hwang S S, Lee P H, Jo S H, et al. Transient behavior of proton exchange membrane fuel cell under non-isothermal condition[J]. Renewable Energy, 2012, 42: 54-59. DOI:10.1016/j.renene.2011.09.016 |
| [3] |
Kim S, Shimpalee S, Van Zee J W. The effect of stoichiometry on dynamic behavior of a proton exchange membrane fuel cell (PEMFC) during load change[J]. Journal of Power Sources, 2004, 135: 110-121. DOI:10.1016/j.jpowsour.2004.03.060 |
| [4] |
Kim S, Shimpalee S, Van Zee J W. The effect of reservoirs and fuel dilution on the dynamic behavior of a PEMFC[J]. Journal of Power Sources, 2004, 137: 43-52. DOI:10.1016/j.jpowsour.2004.05.035 |
| [5] |
Hu G, Fan J. Transient computation fluid dynamics modeling of a single proton exchange membrane fuel cell with serpentine channel[J]. Journal of Power Sources, 2007, 165: 171-184. DOI:10.1016/j.jpowsour.2006.11.084 |
| [6] |
Cho J, Kim H S, Min K. Transient response of a unit proton-exchange membrane fuel cell under various operating conditions[J]. Journal of Power Sources, 2008, 185: 118-128. DOI:10.1016/j.jpowsour.2008.06.073 |
| [7] |
Cho J, Park J, Oh H, et al. Analysis of the transient response and durability characteristics of a proton exchange membrane fuel cell with different micro-porous layer penetration thicknesses[J]. Applied Energy, 2013, 111: 300-309. DOI:10.1016/j.apenergy.2013.05.022 |
| [8] |
Ferng Y M, Su A. A three-dimensional full-cell CFD model used to investigate the effects of different flow channel designs on PEMFC performance[J]. International Journal of Hydrogen Energy, 2007, 32: 4466-4476. DOI:10.1016/j.ijhydene.2007.05.012 |
| [9] |
Sun P T. Modeling studies and efficient numerical methods for proton exchange membrane fuel cell[J]. Computer Methods in Applied Mechanics and Engineering, 2011, 200(47-48): 3324-3340. DOI:10.1016/j.cma.2011.08.007 |
| [10] |
Xing L, Mamlouk M, Scott K. A two dimensional agglomerate model for a proton exchange membrane fuel cell[J]. Energy, 2013, 61: 196-210. DOI:10.1016/j.energy.2013.08.026 |

