放射性统计涨落和电子学噪声等因素会对实测核能谱的定性定量分析产生不利影响。谱线平滑处理可以去除谱线中的噪声，保留谱峰全部重要的特性信息。常用能谱平滑方法有算术滑动平均法（移动平均平滑法）、重心法、快速傅里叶变换法、高斯法、小波分析等^[1-7]，随着研究深入，更多处理方法正在出现。Savitzky等^[3]提出在时域内用多项式卷积计算方法进行最小二乘拟合计算的Savitzky- Golay滤波器（简称SG平滑）。刘永刚^[2]采用B样条法对γ能谱平滑研究，该方法不需设定初值，具有较高的峰形分辨能力，适用于谱线局部平滑；对全谱平滑时需要高阶B样条函数，且平滑速度较慢。黄洪全等^[4]结合核能谱的统计特性，采用高斯混合模型对核能谱进行平滑滤波处理，在模型的多次运算过程中实现更合理的平滑滤波。赵奉奎^[5]针对能量色散X射线荧光光谱，提出平稳小波变换与交叉验证和最优阈值相结合的算法，对能量色散X射线荧光光谱去噪，有效避免Gibbs现象的发生，提高信号的信噪比，减小均方根误差。侯利桥等^[6]根据平滑要求和处理速度，建立不同函数的径向基函数(Radical Basis Function, RBF)神经网络对核能谱进行平滑滤波。

各谱线平滑方法各有优势，并不是在任何情况下总是有效的。MATLAB是一种用于算法开发、数据可视化、数据分析以及数值计算的科学计算软件，具备强大便捷的绘图功能和友好的界面。GUI (Graphical User Interface)是MATLAB的另一个重要特色，利用它可以开发易于使用的人机交互界面。为方便对谱线进行平滑处理，本文基于MATLAB GUI，设计了能够脱离MATLAB运行的可执行界面程序。设计分析工具已实现谱线数据高斯平滑和SG平滑处理，可对测量能谱进行在线实时和离线批量处理。

高斯平滑也称高斯滤波，它是一种按照高斯函数的特性来计算权值的线性平滑滤波器，对抑制服从正态分布的噪声非常有效。高斯滤波对谱图数据进行加权平均，每一个数据点的值，都由其本身与邻域内的其他数据经加权平均后求得。高斯滤波的实现过程可以看作是用滤波模板（或称卷积、掩模）扫描谱图中的每一个数据，用模板确定的邻域内数据的加权平均值去替代模板中心数据点的值^[7-8]。

高斯滤波模板由离散后的正态分布的概率密度函数求得：

式中：σ为滤波器的标准差，表征高斯函数的宽度（决定平滑程度）；r为模板值，数学模拟时一般取整数，高斯模板长度w（w一般取奇数）与r的关系为：w=r×2-1。

下面为实现高斯滤波模板的MATLAB程序：

h= zeros(1, 2*r-1);

for k=1 : 2*r-1

    h(k)=exp(-(k-r)^2/(2*sigma^2))/(sigma* sqrt(2*pi));

end

采用离散卷积滑动变换平滑方法，可以实现能谱数据的快速高斯平滑，其数学算法实质是取测量信号f(n)和高斯滤波函数模板h(n)的卷积。

数据序列f(n)与h(n)的卷积定义为：

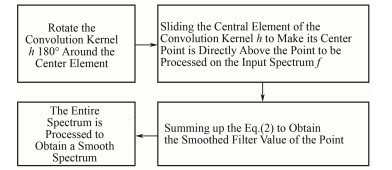
算式中的h称为高斯卷积核。卷积实现高斯滤波的步骤如图 1所示。

图 1

图 1 卷积实现高斯滤波步骤图 Figure 1 Flow chart of convolution Gaussian filter

分析高斯滤波的过程可知，谱线的开头和结尾的r个数据无法滤波，在实际处理谱数据时可采用在谱线数据序列f(n)的前后各补充r个0，实现全谱滤波。

SG平滑最初由Savitzky等^[3]于1964年提出，在数据流平滑除噪中应用普遍。它是一种在时域内基于多项式，通过移动窗口位置，利用偏最小二乘法(Partial Least Squares, PLS)进行最佳拟合的方法。SG平滑算法是对移动平滑算法的改进，其原理是：首先在拟合点x_k的左右两边各取m个数据点，共2m+1个数据，然后对这2m+1个数据进行多项式拟合，并使各个数据点的实际值与拟合值之差的平方和最小，最后移动x_k，做相同计算，完成谱线光滑^{[3, 9-10]}。常用点次的SG平滑公式系数可直接查表获得^[3]，本文采用七点二次平滑系数，见表 1。

表 1

表 1 七点二次的平滑系数 Table 1 Coefficient of seven point two times smoothing 1/42 yk-a yk-2 yk-1 yk yk+1 yk+2 yk+a $\overline {{y_1}} $ 32 15 3 -4 -6 -3 5 $\overline {{y_2}} $ 15 12 9 6 3 0 -3 $\overline {{y_3}} $ 3 9 12 12 9 3 -6 $\overline {{y_k}} $ -4 6 12 14 12 6 -4 $\overline {{y_{n - 2}}} $ -6 3 9 12 12 9 3 $\overline {{y_{n - 1}}} $ -3 0 3 6 9 12 15 $\overline {{y_n}}$ 5 -3 -6 -4 3 15 32

表 1 七点二次的平滑系数 Table 1 Coefficient of seven point two times smoothing

表 1中$\overline {{y_k}} $是所在行为平滑谱线中间各点时的系数，其他各行分别为前面起始点和后面结束点的系数。从表 1中可以写出七点二次平滑公式：

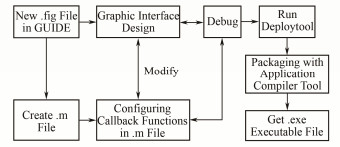
MATLAB GUI设计的方法通常有两种：一是用.m文件代码构建界面；二是直接利用自带的图形界面开发环境(Graph User Interface Developing Environment, GUIDE)来制作界面。GUIDE交互性较强，用户只需在GUIDE中合理布局控件就可以搭建人机交互界面，通过简单的属性设置和少量的代码就可对控件进行控制^[11-12]。本文采用第二种方式，GUI设计步骤如图 2所示。

图 2

图 2 GUI设计流程框图 Figure 2 Block diagram of GUI design

.fig文件主要承载可视化图文界面。.m文件中存储与.fig文件中各控件对应的回调函数，以及方便用于人机交互的uigetfile、listdlg、questdlg等对话框命令。调试完成后的程序用打包工具生成exe可执行文件。

设计的谱线分析工具支持.txt、.xls、.pu（四川新先达测控技术有限公司的CIT系列能谱仪测量数据文件）文件格式，工作界面如图 3所示。界面有“单文件处理”和“文件夹批处理”，通过6个步骤（界面中序号）实现谱线平滑分析。

图 3

图 3 软件界面 Figure 3 Software interface

步骤1中执行“打开文件”时可处理一条谱线，根据后续各步骤选取的功能对谱线平滑处理。处理后的谱数据自动在原文件名末尾加上GS、SG、NH并生成新文件，存储于与原文件同路径的AfterSoomth子目录中。平滑后的各谱线在新窗口中绘图显示。当执行“打开文件夹”时，会对文件夹内选定文件做批处理平滑并输出为新文件，数据处理后不绘图。

分析的实测能谱来源于石墨预衍射X荧光分析仪对U标准样的测量结果。在MATLAB中对实测谱线进行高斯平滑、SG平滑，平滑后的谱线与原始谱线在同一绘图窗口叠加显示，用户可以直观地进行不同滤波方式的谱线比较，此功能在此不赘述。下面针对本谱线分析工具输出的滤波后文件进行数据分析。

为了进一步分析平滑后谱线，本文引入平滑度和相关系数指标。

平滑度是指去噪后信号的差分数平方和与原始信号差分平方和之比，记为r。信号越光滑，平滑度值越小，去噪效果也越好。

式中：f(i)和g(i)分别为能谱平滑前后第i道的数据；n为总道数。r值越趋近于0，平滑效果越好^[13]。

相关系数用于评价平滑信号与原始信号的相似度，记为ρ。ρ越接近于1，则信号相关性越好；当ρ为0时，两者不相关^[14]。相关系数计算公式如式(5)所示。

式中：μ_f、μ_g分别为f(i)和g(i)的均值；σ_f、σ_g分别为f(i)和g(i)的标准差。

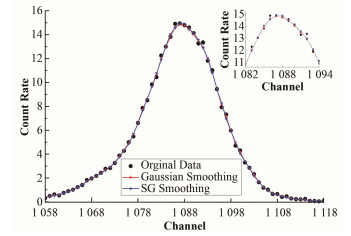
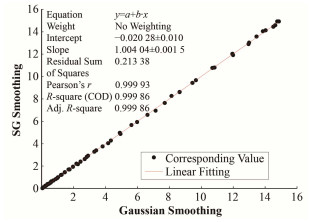
选取500 μg∙mL^-1的U标准样的实测能谱，对其进行一次高斯平滑和SG平滑，高斯平滑参数如下：窗口宽度为7，滤波器标准差σ为0.75；SG平滑采用七点二次多项式滤波。原始能谱和平滑后数据分别用统计敏感的非线性迭代剥峰算法(Statistics-sensitive Nonlinear Iterative Peak-clipping, SNIP)方法扣除背景，从上述处理后的数据中截取U特征峰对应的1058~1118道区域数据绘图，如图 4所示。对上述两种平滑数据做线性拟合，如图 5所示，可得拟合优度R²为0.99986。由此可以看出：合适平滑参数的一次高斯平滑与一次SG平滑在特征峰上平滑效果相差不大。

图 4

图 4 SNIP方法扣除背景后的U特征峰 Figure 4 U characteristic peak after deducting background by SNIP method

图 5

图 5 高斯平滑与SG平滑结果线性分析 Figure 5 Linear analysis of Gaussian smoothing and SG smoothing results

分别选取含量为1 μg∙mL^-1、5 μg∙mL^-1、10μg∙mL^-1、50 μg∙mL^-1、100 μg∙mL^-1、500 μg∙mL^-1和1000 μg∙mL^-1的U标准样实测数据，保持上述平滑参数不变，进行一次高斯平滑和SG平滑，截取1058~1118道U特征峰平滑后数据进行分析，平滑度和相关系数指标如表 2所示。分析表 2数据可知，高斯平滑的相关系数指标较好；随着特征峰幅值的增加，两种平滑方式的平滑度均变差，低含量时，SG平滑的平滑度优于高斯平滑，特征峰幅值较大时，高斯平滑较优。

表 2

表 2 一次平滑后的U特征峰能谱数据 Table 2 Energy spectrum data of U characteristic peaks after signal smoothing U含量 Contents of U / μg∙mL−1 平滑度r Smoothness 相关系数ρ Correlation coefficient SG七点二次平滑Seven-spot double smoothing of SG 高斯平滑Gaussian smoothing SG七点两次平滑Seven-spot double smoothing of SG 高斯平滑Gaussian smoothing 1 0.096 89 0.179 22 0.903 57 0.956 40 5 0.231 90 0.317 12 0.984 30 0.993 24 10 0.210 75 0.254 94 0.981 25 0.992 68 50 0.618 53 0.638 50 0.998 09 0.999 19 100 0.740 32 0.741 46 0.999 01 0.999 51 500 0.856 79 0.848 73 0.999 53 0.999 76 1 000 0.964 33 0.952 08 0.999 89 0.999 95

表 2 一次平滑后的U特征峰能谱数据 Table 2 Energy spectrum data of U characteristic peaks after signal smoothing

选取500 μg∙mL^-1的U标准样的实测能谱，对原始能谱数据分别做不同次数和不同参数的高斯平滑和SG平滑，然后截取U特征峰对应的1058~1118道区域平滑后数据进行分析，结果如表 3所示。

表 3

表 3 多次平滑后的U特征峰能谱数据 Table 3 Energy spectrum data of U characteristic peaks after multiple smoothing 平滑方式 Smoothing method 平滑次数 Smoothing times 标准差σ Standard deviation 峰值 Peak 峰位道址 Peak position 平滑度r Smoothness 相关系数ρ Correlation coefficient SG五点两次平滑Five-spot double smoothing of SG 1 ― 15.126 29 1 087 0.868 50 0.999 61 5 ― 15.069 24 1 087 0.851 38 0.999 62 10 ― 15.033 85 1 087 0.846 80 0.999 58 20 ― 14.991 07 1 088 0.841 74 0.999 54 30 ― 14.988 95 1 088 0.838 30 0.999 51 SG七点两次平滑Seven-spot double smoothing of SG 1 ― 15.069 05 1 087 0.856 79 0.999 53 5 ― 14.988 72 1 088 0.840 28 0.999 53 10 ― 14.976 14 1 088 0.833 33 0.999 47 20 ― 14.930 73 1 088 0.822 78 0.999 39 30 ― 14.877 58 1 088 0.813 38 0.999 31 高斯平滑Gaussian smoothing 1 0.50 15.045 46 1 087 0.909 29 0.999 95 0.75 15.003 35 1 087 0.848 73 0.999 76 1.00 14.931 81 1 087 0.828 28 0.999 63 1.25 14.846 06 1 087 0.813 03 0.999 54 5 0.50 14.917 35 1 087 0.827 13 0.999 66 0.75 14.664 53 1 088 0.781 66 0.999 34 1.00 14.414 65 1 088 0.737 07 0.998 90 1.25 14.133 95 1 088 0.691 55 0.998 20 10 0.50 14.748 32 1 087 0.797 14 0.999 46 0.75 14.342 58 1 088 0.725 03 0.998 74 1.00 13.876 70 1 088 0.652 69 0.997 35 1.25 13.383 33 1 088 0.583 69 0.995 16 20 0.50 14.492 51 1 088 0.750 54 0.999 06 0.75 13.746 98 1 088 0.633 89 0.996 85 1.00 12.958 15 1 088 0.528 96 0.992 65 1.25 12.200 45 1 088 0.440 85 0.986 58 30 0.50 14.251 32 1 088 0.710 20 0.998 52 0.75 13.219 21 1 088 0.562 06 0.994 27 1.00 12.213 34 1 088 0.442 21 0.986 71 1.25 11.308 27 1 088 0.350 45 0.976 70

表 3 多次平滑后的U特征峰能谱数据 Table 3 Energy spectrum data of U characteristic peaks after multiple smoothing

分析表 3中不同σ时的一次高斯平滑处理数据可知，选择较大的σ，有利于在维持较好的相关系数时，提升处理后谱线的平滑度。

分析表 3中数据可以看出，SG七点二次平滑优于五点二次平滑的平滑度指标，前者只需较少的平滑次数就可对特征峰所在的道址进行矫正。在高斯平滑中，比较相同平滑次数下不同σ，以及相同σ不同平滑次数两组数据可知，多次平滑和较大的σ可改善谱线的平滑度。在相关系数指标上，虽然相关系数指标会随着平滑次数的增多有所下降，但利用SG五点二次平滑和七点二次平滑分别作单次和多次平滑的相关系数均在0.999以上；同理，高斯平滑中，增大平滑次数和σ，均会引起相关系数的下降，但其值仍能维持在0.97以上。以上各种方式的平滑数据，从U特征峰峰值来看，较大的参数设置会引起特征峰峰值的下降。

在算法实现上，高斯平滑参数w与σ的设置较灵活，但运算中需采用矩阵，计算较复杂，而SG平滑可通过查表获取常用点次的平滑公式。在MATLAB 2016b平台上测试，执行10次高斯平滑约需2700 ms，10次SG平滑约需1300 ms。综合比较算法与代码执行时间可知，高斯平滑的参数选取更灵活，而SG平滑的算法更简洁，程序运行效率更高。

本文以MATLAB GUI为平台设计了对谱数据进行在线实时处理与离线批量分析的处理工具。文中引入了相关系数来评价平滑后谱数据与原始数据的相似度。对平滑后谱线分析发现，在维持较好相关系数指标条件下，当谱峰幅值较小时，SG平滑的平滑度指标较优，当谱峰幅值较大时，高斯平滑较好。在算法实现上，SG平滑的多项式系数可查表获得，算法更简洁，而高斯平滑的参数选择更加灵活，但运算中需用到卷积与矩阵，在代码执行时间上，SG平滑优于高斯平滑，因此SG平滑更适于嵌入式设备中的谱线平滑应用。实际工程应用中，应综合考虑应用需求，在维持较好平滑度和相关系数指标的情况下，合理选择平滑方式与平滑参数。