Pu(钚)是一种重要的核工业原料,其结构对温度十分敏感,其熔点为913 K,在熔点以下存在6种同素异形体,单斜α-Pu[1]是钚在397 K下的结构形式;温度升高就会形成体心单斜结构的β-Pu[2];升温至488 K出现斜方的γ-Pu[3],而结构为面心正方的δ-Pu[4]在593 K后才能出现,在纯钚中掺杂Ga能获得常温下面心正方的Pu-Ga合金;736 K是δ-Pu与体心四方δ′-Pu的分界温度;随后升温到755 K出现体心正方的ε-Pu。钚元素的不同结构的相对辐照表现出不同的性质,由于钚在衰变过程中存在自辐照,因此,人们在不同条件下获得的钚元素各相的稳定性一直存在争议。例如,δ′-Pu相在Lord[5]的研究中还未被发现。直到1954年,来自洛斯·阿拉莫斯国家实验室的Jette[6]对钚进行性质总结,人们才对Pu的相稳定性得到了普遍的认可。除此之外,在高温、限定压力范围下有第7种相(ζ)[7]存在。由于这么多种同素异形体的存在,改变温度时钚的状态很容易随之改变,使得钚的加工、储存和运输都十分困难。此外,钚还具有自辐照效应[8-9],发射出α粒子,使得晶体内出现疲劳现象,同时也会影响纯钚的相稳定性。因此,关注纯Pu在使用过程中相的稳定性及温度区间具有一定的必要性。
国内外对于纯Pu进行了广泛的研究,例如,钚的原子结构、超导性质、辐照损伤等。Schwartz等[10]提出钚的微结构、物理性质、机械性质与原子结构息息相关。Espinosa等[11]利用XAFS (X-ray Absorption Fine Structure)探测α-Pu局部的原子结构,发现Pu局部中的无序具有杂质依赖性。Sarrao等[12-13]讨论了PuCoGa5单晶的超导性,转变温度为18.5 K,并且其超导性由自旋波动介导,具有非传统性。辐照损伤在核材料的使用过程中是不可避免的,如核燃料、结构材料[14]等。在钚中的辐照损伤[15-16]是经过各种时间和距离尺度演变的复杂事件的积累影响,主要辐照效应有氦气泡形成、空位肿胀、蠕变和弛豫。此外,辐照同时也会影响钚原本的性质,如超导性[17]、电阻性[18]等。Jutier[17]的研究结果表明:PuCoGa5和PuRhGa5有相似的超导体特征,但二者的超导性对辐射损伤的敏感度十分不同。Elliott将富含α-Pu和不富含α-Pu的238Pu进行比较,发现富含α-Pu的238Pu的电阻性升高,并将其归因于辐照产生的间隙原子和空位。Liu等通过考虑辐照产生的间隙原子及空位形成的弹道混合效应(Ballistic effect),建立了辐照条件下有效自由能模型,该模型已被成功应用于U-Nb合金在辐照下的相图计算[19]。虽然目前对钚的研究有许多,但对于钚的几种相在辐照条件下的稳定性的研究鲜见报道。辐照下纯钚的相稳定性与钚及其合金性质具有重要联系,研究其众多同素异构体的相变行为,对钚基核能源使用、核废料后期处理等都十分重要。
本文基于辐照条件下的有效自由能模型,重点研究辐照时间对体系自由能的贡献,建立纯钚在辐照条件下与辐照时间相关的过剩自由能模型,结合钚的热力学平衡态自由能模型,计算得到钚在不同辐照条件下的总自由能,研究纯钚在辐照条件下的各个同素异构体相稳定性,计算得到纯钚动态弹道效应下的相图,为钚基核燃料的设计、使用和辐照性能研究提供理论参考。
1 热力学模型 1.1 纯组元热力学模型纯组元热力学建立是开展复杂体系热力学研究的基础。热力学状态函数G就是吉布斯(Gibbs)自由能。
| $ G = H-T{S_{\rm{p}}} $ | (1) |
| $ H = \int_0^T {{C_{\rm{p}}}{\rm{d}}T + H(0_{}^{}\;{\rm{K}})} $ | (2) |
式中:H(0 K)是热力学零度时的焓;Cp为恒压热容。
| $ {S_{\rm{p}}} = \int_0^T {\frac{{{C_{\rm{p}}}}}{T}{\rm{d}}T + S(0_{}^{}\;{\rm{K}})} $ | (3) |
式中:S(0 K)是热力学零度下的熵,根据热力学第三定律,可以认为单组元相在热力学零度下的熵S(0 K)=0。结合式(1)、(2)、(3),所以单组元相的Gibbs自由能为:
| $ G = \int_0^T {{C_{\rm{p}}}{\rm{d}}T-\int_0^T {\frac{{{C_{\rm{p}}}}}{T}{\rm{d}}T + H(0_{}^{}\;{\rm{K}})} } $ | (4) |
通常,恒压热容Cp与温度之间具有如下关系:
| $ {C_{\rm{p}}} = a + bT + c{T^{-2}} $ | (5) |
将式(5)代入式(4)并积分,能得到恒压下,纯组元的Gibbs自由能是温度的函数,可用式(6)表示:
| $ G = a' + b'T + c'T\ln T + d'{T^2} + e'{T^{-1}} $ | (6) |
这就是自由能与温度的关系,a'、b'、c'、d'、e'均为待定参数。一般情况下,式(6)受Cp=a+bT+cT-2的形式和适用温度范围的制约,所以通常根据温度进行划分(即在各温度区间内对Cp和Gibbs设定不同的变量参数),通过采用分段函数的形式来完整表示。在计算过程中,区间不能随意划分,要求Gibbs自由能和Cp值保持整体的连续性。
1.2 辐照条件下的热力学模型在得到无辐照下的纯组元热力学模型后,探讨辐照条件下的热力学模型是研究纯钚稳定性的重点。在Cahn-Hilliard[20]扩散方程的基础上,Martin提出了辐照条件下有效自由能模型。他将辐照引起的弹道混合(弹道效应)看成是过剩原子扩散,由此可得到原子扩散通量为:
| $ J =-M\nabla \frac{{\delta G}}{{\delta c}}-{D^{\rm{b}}}{\nabla _c} $ | (7) |
| $ J =- M\left[{\left( {G'' + \frac{{{D^{\rm{b}}}}}{M}} \right)\frac{{\partial c}}{{\partial x}}-2\kappa \frac{{{\partial ^3}c}}{{\partial {x^3}}}} \right] $ | (8) |
式中:G"为纯钚Gibbs自由能的二次导数;c为钚-空位系统中空位的浓度;κ为能量梯度系数;Db为弹道扩散系数;M为原子迁移率。类比Cahn-Hilliard扩散方程与式(8)可以看出,式(8)等式右边第一项小括号中的表达式可定义为辐照条件下有效自由能的二阶导数,即:
| $ \phi '' = G'' + \frac{{{D^{\rm{b}}}}}{M} $ | (9) |
其中:
| $ {D^{\rm{b}}} = \eta {K_0}{d^2} $ | (10) |
式中:d为跳跃距离;通常原子离位率(K0)的取值范围为10-9~10-2dpa·s-1 [21]。η的取值范围为1~10000dpa-1 [22]。本文中,辐照强度是通过K0和η的大小来决定的,辐照强度增大,K0和η也随之增大。
由式(9)可知,弹道自由能K的二次导数为:
| $ K'' = \frac{{{D^{\rm{b}}}}}{M} $ | (11) |
其中:
| $ M = \frac{{c(1-c)\tilde D}}{{RT}} $ | (12) |
| $ \tilde D = c{D_{{\rm{Pu}}}} + (1-c){D_{{\rm{va}}}} $ | (13) |
式中:
| $ {D_{{\rm{va}}}} = D_{\rm{a}}^{\rm{v}} = {a_{\rm{v}}}{a^2}{v_0}\exp \left( {\frac{{S_{\rm{m}}^{\rm{v}} + S_{\rm{f}}^{\rm{v}}}}{k}} \right)\exp \left( {\frac{{-E_{\rm{m}}^{\rm{v}}-E_{\rm{f}}^{\rm{v}}}}{{kT}}} \right) $ | (14) |
本文只考虑空位机制和间隙机制的前提下,钚-空位系统中Pu原子的扩散系数可表示为:
| $ {D_{{\rm{Pu}}}} = {f_{\rm{v}}}(C_{\rm{v}}^{{\rm{irr}}} + C_{\rm{v}}^0){D_{\rm{v}}} + {f_{\rm{i}}}(C_{\rm{v}}^{{\rm{irr}}} + C_{\rm{v}}^0){D_{\rm{v}}} $ | (15) |
其中:
| $ \left\{ \begin{array}{l} C_{\rm{v}}^0 = \exp (S_{\rm{f}}^{\rm{v}}/k)\exp (-E_{\rm{f}}^{\rm{v}}/kT)\\ {D_{\rm{v}}} = {a_{\rm{v}}}{a^2}{v_0}\exp (S_{\rm{m}}^{\rm{v}}/k)\exp (-E_{\rm{m}}^{\rm{v}}/kT)\\ C_{\rm{i}}^0 = \exp (S_{\rm{f}}^{\rm{i}}/k)\exp (-E_{\rm{f}}^{\rm{i}}/kT)\\ {D_{\rm{i}}} = {a_{\rm{i}}}{a^2}{v_0}\exp (S_{\rm{m}}^{\rm{i}}/k)\exp ( - E_{\rm{m}}^{\rm{i}}/kT) \end{array} \right. $ | (16) |
式中:Cv为空位浓度;a为晶格常数;Smv、Sfv分别为空位迁移熵和空位形成熵(在计算中通常被看成0),Emv、Efv分别为空位迁移能和空位形成能;v0为原子振动频率(~1013 s-1);av、ai为与结构相关系数(本研究中av=1、ai=0.5)[20];fv、fi为扩散相关系数(本研究认为是1)。
式(15)中的Cvirr、Ciirr分别是辐照下产生的空位浓度、填隙原子浓度。点缺陷在体系中的变化大致可分为三类:1)缺陷产生率;2)缺陷间的相互作用;3)扩散进、出局部体材料。前一种变化导致点缺陷增多,而后两者都将导致点缺陷的减少。本研究只考虑空位-填隙原子复合以及点缺陷与势阱相互作用这两种。因此,这些竞争效应的速率方程可表示为:
| $ \frac{{{\rm{d}}C_{\rm{v}}^{{\rm{irr}}}}}{{{\rm{d}}t}} = {K_0}-{K_{{\rm{iv}}}}{C_{\rm{i}}}{C_{\rm{v}}}-{K_{{\rm{vs}}}}{C_{\rm{v}}}{C_{\rm{s}}} $ | (17) |
| $ \frac{{{\rm{d}}C_{\rm{i}}^{{\rm{irr}}}}}{{{\rm{d}}t}} = {K_0}-{K_{{\rm{iv}}}}{C_{\rm{i}}}{C_{\rm{v}}}-{K_{{\rm{is}}}}{C_{\rm{i}}}{C_{\rm{s}}} $ | (18) |
式中:K0为缺陷产生率,即每个原子每秒钟的离位数(dpa·s-1);Kiv为空位-填隙原子复合系数;Kis为空位-势阱反应系数;Kvs为填隙原子-空位反应系数;Cs是势阱浓度。Kiv、Kis和Kvs可表示为:
| $ \left\{ \begin{array}{l} {K_{{\rm{iv}}}} = 4{\rm{ \mathit{ π} }}{r_{{\rm{iv}}}}({D_{\rm{i}}} + {D_{\rm{v}}}) \approx 4{\rm{ \mathit{ π} }}{r_{{\rm{iv}}}}{D_{\rm{i}}}\\ {K_{{\rm{is}}}} = 4{\rm{ \mathit{ π} }}{r_{{\rm{is}}}}{D_{\rm{i}}}\\ {K_{{\rm{vs}}}} = 4{\rm{ \mathit{ π} }}{r_{{\rm{vs}}}}{D_{\rm{v}}} \end{array} \right. $ | (19) |
式中:riv、rvs和ris为由下标所表示物质间的相互作用半径。
在考虑只含位错的低势阱浓度的情况下,Cs可表示为:
| $ {C_{\rm{s}}} = {\rho _{\rm{d}}}/4{\rm{ \mathit{ π} }}{r_{{\rm{vs}}}} $ | (20) |
式中:纯钚的位错密度ρd约为1010 m-2 [23]。
在辐照条件下,入射粒子和晶格原子碰撞产生了Frenkel缺陷,从而增加体系的点缺陷浓度,同时缺陷存在各种反应(空位与填隙原子相互复合,缺陷与势阱湮灭),在另一方面减少点缺陷,因此点缺陷的浓度的增长速率会不断变化。经过一段时间后,最终会形成一种动态平衡。填隙原子浓度、空位浓度随时间变化可分为4个阶段[22]:
第一阶段:0≤t < t1。
开始阶段,整体点缺陷浓度的值很低,不足以使填隙原子与空位相结合,或者缺陷与势阱相湮灭,所以空位浓度与填隙原子浓度相当,点缺陷浓度上升是根据dC/dt=K0。
| $ C_{\rm{v}}^{{\rm{irr}}} = C_{\rm{i}}^{{\rm{irr}}} = {K_0}t $ | (21) |
第二阶段:t1≤t < t2。
随浓度上升,点缺陷开始互相结合,由于其产生率与二者的结合率互补,缺陷浓度相持平。
| $ C_{\rm{v}}^{{\rm{irr}}} = C_{\rm{i}}^{{\rm{irr}}} = {({K_0}/{K_{{\rm{iv}}}})^{1/2}} $ | (22) |
第三阶段:t2≤t < t3。
进一步发展,缺陷会不断陷入势阱,由于Di > Dv,相对于空位会有更多的填隙原子陷入势阱。
| $ \left\{ \begin{array}{l} C_{\rm{v}}^{{\rm{irr}}} = {[{K_0}{K_{{\rm{is}}}}{C_{\rm{s}}}t/{K_{{\rm{iv}}}}]^{1/2}}\\ C_{\rm{i}}^{{\rm{irr}}} = {[{K_0}/{K_{{\rm{iv}}}}{K_{{\rm{is}}}}{C_{\rm{s}}}t]^{1/2}} \end{array} \right. $ | (23) |
第四阶段:t≥t3。
最后产生率与空位、填隙原子二者的陷入势阱率、结合率持平,于是缺陷浓度最终达到一种平衡。
| $ \left\{ \begin{array}{l} C_{\rm{v}}^{{\rm{irr}}} =-\frac{{{K_{{\rm{is}}}}{C_{\rm{s}}}}}{{2{K_{{\rm{iv}}}}}} + {\left( {\frac{{{K_0}{K_{{\rm{is}}}}}}{{{K_0}{K_{{\rm{vs}}}}}} + \frac{{K_{{\rm{is}}}^2C_{\rm{s}}^2}}{{4K_{{\rm{iv}}}^2}}} \right)^{1/2}}\\ C_{\rm{v}}^{{\rm{irr}}} =-\frac{{{K_{{\rm{vs}}}}{C_{\rm{s}}}}}{{2{K_{{\rm{iv}}}}}} + {\left( {\frac{{{K_0}{K_{{\rm{vs}}}}}}{{{K_{{\rm{iv}}}}{K_{{\rm{is}}}}}} + \frac{{K_{{\rm{vs}}}^2C_{\rm{s}}^2}}{{4K_{{\rm{iv}}}^2}}} \right)^{1/2}} \end{array} \right. $ | (24) |
其中:
| $ \left\{ \begin{array}{l} {t_1} = {({K_0}{K_{{\rm{iv}}}})^{-1/2}}\\ {t_2} = {({K_{{\rm{is}}}}{C_{\rm{s}}})^{-1}}\\ {t_3} = {({K_{{\rm{vs}}}}{C_{\rm{s}}})^{-1}} \end{array} \right. $ | (25) |
由式(11)、(12)、(13)可知,在辐照条件下的弹道自由能可通过对式(11)二次积分获得。Ravishankar等[24]借鉴化学势的定义引入弹道势,并利用Gibbs-Duhem关系,将K"的二次积分化解成两个一次积分的加和。因此,本研究在假设Db、DPu及Dva与浓度无关的前提下,积分计算得到K的最终表达式为:
| $ \begin{array}{c} K = \frac{{(1- c)RT{D^{\rm{b}}}}}{{{D_{{\rm{Pu}}}}}}\{ \ln (1- c)- \ln [c{D_{{\rm{Pu}}}} + (1-c){D_{{\rm{va}}}}]\} + \\ \frac{{cRT{D^{\rm{b}}}}}{{{D_{{\rm{va}}}}}}\{ \ln c - \ln [c{D_{{\rm{Pu}}}} + (1-c){D_{{\rm{va}}}}]\} + \\ c{D^{\rm{b}}}RT(\frac{{\ln {D_{{\rm{Pu}}}}}}{{{D_{{\rm{va}}}}}} -\frac{{\ln {D_{{\rm{va}}}}}}{{{D_{{\rm{Pu}}}}}}) + {D^{\rm{b}}}RT\frac{{\ln {D_{{\rm{va}}}}}}{{{D_{{\rm{Pu}}}}}} \end{array} $ | (26) |
该式为辐照条件下的弹道自由能表达式,加上Gibbs自由能得到最终有效自由能(ϕ)的表达式为:
| $ \phi {\rm{ = }}G + K $ | (27) |
研究纯钚在辐照条件下的相稳定性,首先要对不同辐照条件下的有效自由能进行研究。有效自由能主要受到体系中位错密度(ρd)、K0、原子置换数(η)、温度(T)的影响。
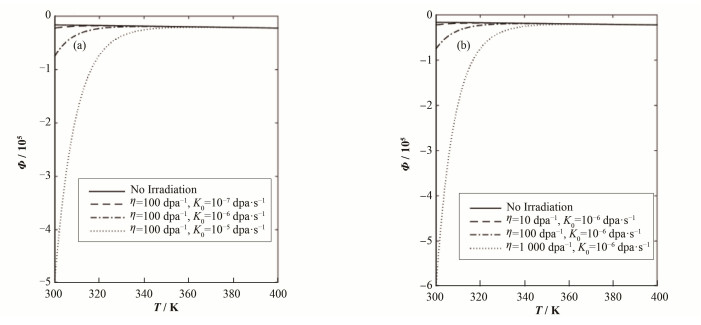
本研究所用的相关扩散参数是由Uberuaga[25]、Berlu[26]、Valone[27]运用分子动力学的嵌入原子法得来,如表 1所示。扩散系数中,文献中有具体描述的是δ-Pu[25-29],其他五相的参数根据空位形成能、迁移能和间隙迁移能与键能、键数有关[30],进行合理假设。其中,间隙形成能的文献较少,且数值小,将其他五相的间隙形成能设置与δ-Pu相同。图 1是不同辐照强度对纯钚自由能的影响作用。图 1(a)、(b)分别是δ-Pu的Gibbs自由能在η=100 dpa-1、K0 =10-6 dpa·s-1情况下随不同K0和η值的变化情况。
|
图 1 不同K0值(a)和η值(b)对纯钚的吉布斯自由能的影响 Figure 1 Effect of different values of K0 (a) and η (b) on the Gibbs free energy of pure Pu |
| 表 1 本研究中所使用的扩散数据(包括各相的缺陷形成能与迁移能) Table 1 The diffusion data used in this study including the defect formation energy and migration energy of each phase |
图 1中实线是无辐照下的自由能随温度(T)的变化情况,随着K0、η值的增大,自由能数值呈下降的现象。可明显观察到,低温下的自由能数值急剧下降,且下降的幅度越来越大;360 K以上的自由能变化不大,甚至不变化。由图 1可观察到代表辐照强度的K0、η,增加其值对自由能的作用相当。
计算结果表明:辐照对系统自由能的影响比较明显,这主要是由于在高温下,原子热运动较为激烈,热扩散迅速,产生多的点缺陷,而纯钚中原本的点缺陷平衡浓度开始就比较高。因此,辐照条件下形成的点缺陷浓度相对较小,从点缺陷浓度的角度来看,辐照对在高温情况下的自由能的贡献较小。低温条件下的热扩散相当缓慢,原本的热缺陷平衡浓度就低,而辐照使得体系中的缺陷浓度获得了显著的提高,并逐渐超过起初热平衡的空位浓度占据了主导地位,导致体系自由能较大幅度降低。
2.2 纯钚在辐照条件下的相稳定性考虑到辐照强度、辐照时间等对纯钚的相稳定性均有影响,本研究通过改变辐照强度及辐照时间,分别研究二者的变化和耦合作用对于纯钚不同温度下相稳定性的影响。
辐照的强度大小可由K0、η的具体值表征[21]。首先,研究具体不同K0值的影响。图 2是当η= 10000dpa-1时,不同K0值对纯钚随时间相变化的影响情况。随K0增大,γ-Pu在低温下出现的时间越来越短,且开始出现的温度逐渐升高。随时间增长,三种情况在低温下出现的γ-Pu相的温度区间在变宽,到最后渐渐稳定下来。在最后时间t=1.5×109 s时,K0值大的温度区间会稍宽一些。除此之外,随K0增大α-Pu到β-Pu的相变温度有较为明显的升高。要强调的是,在图 2(c)中,K0=0.01 dpa·s-1的辐照下,刚出现γ-Pu相的温度较高,随后慢慢降低。高温下,钚的相区基本不发生变化。

|
图 2 当η=10000 dpa-1时,不同K0值对纯钚随时间的相变化影响 (a) K0=0.0005 dpa·s-1,(b) K0=0.001 dpa·s-1,(c) K0=0.01 dpa·s-1 Figure 2 Effect of different K0 on the phase stability of pure plutonium over time when η=10000 dpa-1 (a) K0=0.0005 dpa·s-1, (b) K0=0.001 dpa·s-1, (c) K0=0.01 dpa·s-1 |
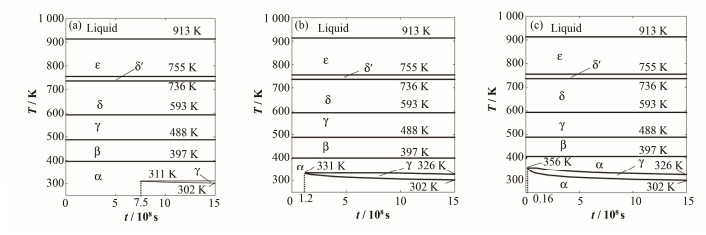
为探讨不同η值对纯钚相区的影响,本文分别计算了η值对纯钚的相区随时间的变化情况,结果如图 3所示。η的物理意义是每次离位引起的原子置换数,其值与晶体结构、辐照强度相关,辐照强度增大,η值会增大。首先,随η增大,γ-Pu在低温下出现的时间越来越短,且开始出现的温度逐渐升高。随时间增长,三种情况在低温下出现的γ-Pu相的温度区间在变宽,到最后渐渐稳定下来。当t=1.5×109 s时,η值大的温度区间会稍宽一些。以上结果与图 2类似。除此之外,随η值的增大,从α-Pu到β-Pu的相变温度同样有较为明显的升高。要强调的是,在图 3(c)中,当η=10000 dpa-1时,γ-Pu相稳定出现的温度较高,随后慢慢降低。同样高温下,钚的相区无明显变化。
|
图 3 当K0=0.01 dpa·s-1时,不同η值对纯钚随时间的相变化影响 (a) η=100 dpa-1,(b) η=1000 dpa-1,(c) η=10000 dpa-1 Figure 3 Effect of different η on the phase stability of pure plutonium over time when K0=0.01 dpa·s-1 (a) η=100 dpa-1, (b) η=1000 dpa-1, (c) η=10000 dpa-1 |
以上是研究了不同的辐照强度下,纯钚在不同温度下的相随时间的变化。而长时间辐照的累积对材料相变会有影响,Elliott[32]、Troshev[33]等发现辐照导致了α-Pu的稳定。钚本身就具有自辐照,虽然自辐照强度极低但在几十年间也会产生影响[15],当t=1.5×109 s(约为47.6 a)时,不同K0值下纯钚各相转变温度随η值的变化影响情况如图 4所示。随K0增大,γ-Pu在低温下出现需要的最小η值越来越小,但低温下α-Pu到γ-Pu的相变温度均为302 K。随η增长,三种情况在低温下出现的γ-Pu相的温度区间均在变宽,且K0值大的最终温度区间最大。除此之外,在图 4(c)中,K0=0.01 dpa·s-1的辐照下,α-Pu到β-Pu的相变温度有较为明显的升高,辐照驱使了α-Pu的稳定。高温下钚的相区基本不发生变化。

|
图 4 当t=1.5×109 s时,不同K0值对纯钚随η的相变化的影响 (a) K0=0.0005 dpa·s-1,(b) K0=0.001 dpa·s-1,(c) K0=0.01 dpa·s-1 Figure 4 Effect of different K0 on the phase transformation of pure plutonium over the value of η when t=1.5×109 s (a) K0=0.0005 dpa·s-1, (b) K0=0.001 dpa·s-1, (c) K0=0.01 dpa·s-1 |
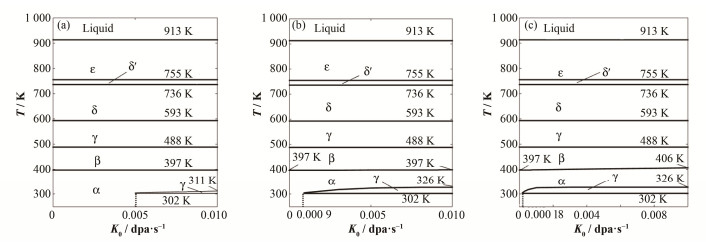
同样,当t=1.5×109 s时,不同η值对纯钚随K0值的相区变化影响的计算结果如图 5所示。随η值增大,γ-Pu在低温下出现需要的最小K0值越来越小,但低温下α-Pu到γ-Pu的相变温度均为302 K。随K0值增大,三种情况在低温下出现的γ-Pu相的温度区间在变宽,并最终趋于稳定。之外,在图 5(c)中,当η=10000 dpa-1时,α-Pu到β-Pu的相变温度有较为明显的升高。高温下钚的相转变温度也基本不发生变化。
|
图 5 当t=1.5×109 s时,不同η值对纯钚随K0的相变化的影响 (a) η=100 dpa-1,(b) η=1000 dpa-1,(c) η=10000 dpa-1 Figure 5 Effect of different η on the phase transformation of pure plutonium over the value of K0 when t=1.5×109 s (a) η=100 dpa-1, (b) η=1000 dpa-1, (c) η=10000 dpa-1 |
辐照效应的温度依赖性是核废料处理的一个重要考虑因素,因为影响储存温度的因素极多,例如时间、核废料装载量、埋藏深度、周围介质的性质、改变的地质环境和核废料的自身情况(微裂、广泛无序)等条件[34]。本研究主要针对纯钚在辐照条件下,考虑弹道混合效应(Ballistic effect)时的缺陷的动态平衡过程,空位和间隙等缺陷在辐照作用下的不断增加和积累,使得辐照增强的扩散和热激活成为可能[10],并在一定辐照强度和时间下达到动态平衡。辐照强度与辐照时间的增加,其效果都是辐照影响的累积。在以上计算结果中,α-Pu相在辐照条件下在低温有稳定的趋势。这是由于辐照而形成的晶格点缺陷会使自由能产生变化,从而改变其稳定性[33]。同时,随着时间增长,在低温下,γ-Pu相区稳定出现,且温度区间逐渐扩大;随辐照强度的增强,出现γ-Pu相的时间逐渐缩短。不同辐照条件下,γ-Pu的有效自由能在6种同素异构体中最低,从而改变了各相自由能的相对大小,导致γ-Pu在低温下出现。在接近室温条件下,研究者们一直以来能得到的是α-Pu或者纯钚中掺杂少量Ga的δ-Pu,本研究则提供了γ-Pu稳定的另一种影响因素。
3 结语本文通过考虑辐照条件下的空位缺陷增值对热力学自由能的贡献,建立了辐照条件下的有效自由能模型,研究了辐照强度、辐照时间对纯钚的相稳定性的影响。结果表明:辐照对于低温下的纯钚相属性影响较大,在低温下出现γ-Pu稳定的相区,且随着辐照强度增强和辐照时间的增加,γ-Pu稳定存在的温度区间就越大;对于高温下的纯钚相属性影响较小。
| [1] |
Zachariasen W H, Ellinger F. Crystal structure of alpha-plutonium metal[J]. Journal of Chemical Physics, 1963, 16(8): 777-783. DOI:10.1063/1.1743837 |
| [2] |
Zachariasen W H, Ellinger F H. The crystal structure of beta plutonium metal[J]. Acta Crystallographica, 1963, 16(5): 369-375. DOI:10.1107/S0365110X63000992 |
| [3] |
Zachariasen W H. The crystal structure of gamma plutonium[R]. Los Alamos Scientific Laboratory, 1951.
|
| [4] |
Zachariasen W H, Ellinger F H. Crystal chemical studies of the 5 f -series of elements XXIV:the crystal structure and thermal expansion of γ-plutonium[J]. Acta Crystallographica, 1955, 8(7): 431-433. DOI:10.1107/S0365110X55001357 |
| [5] |
Lord W B H. Some physical properties of metallic plutonium[J]. Nature, 1954, 173(4403): 534-535. DOI:10.1038/173534a0 |
| [6] |
Jette E R. Some physical properties of plutonium metal[J]. Journal of Chemical Physics, 1955, 23(2): 365-368. DOI:10.1063/1.1741970 |
| [7] |
Baker R D, Hecker S S, Harbur D R. Plutonium a wartime nightmare but a metallurgist's dream[M]. New Mexico: Los Alamos Science, 1983, 142-158.
|
| [8] |
Baclet N, Oudot B, Grynszpan R, et al. Self-irradiation effects in plutoniumalloys[J]. Journal of Alloys & Compounds, 2007, s444-445(24): 305-309. DOI:10.1016/j.jallcom.2006.10.156 |
| [9] |
Troshev A V, Lyasota A M. Effect of self-irradiation on the parameters of the α→β transformation of unalloyed plutonium[J]. Physics of Metals & Metallography, 2010, 109(6): 621-625. DOI:10.1134/S0031918X10060086 |
| [10] |
Schwartz A J, Cynn H, Blobaum K J M, et al. Atomic structure and phase transformations in Pu alloys[J]. Progress in Materials Science, 2009, 54(6): 909-943. DOI:10.1016/j.pmatsci.2009.03.003 |
| [11] |
Espinosa F J, Villella P, Lashley J C, et al. Local atomic structure of α-Pu[J]. Physical Review B, 2001, 63(63): 174111. DOI:10.1103/PhysRevB.63.174111 |
| [12] |
Sarrao J L, Thompson J D, Moreno N O, et al. Discovery of plutonium-based superconductivity[J]. Journal of Physics Condensed Matter, 2003, 15(28): S2275-S2278. DOI:10.1088/0953-8984/15/28/368 |
| [13] |
Sarrao J L, Morales L A, Thompson J D. Superconductivity:a new window on plutonium's complexity[J]. JOM, 2003, 55(9): 38-40. DOI:10.1007/s11837-003-0028-8 |
| [14] |
李萌, 范红玉, 崔荷敬, 等. 低能氦离子辐照诱导的钨材料结构演化[J]. 核技术, 2017, 40(10): 100201. LI Meng, FAN Hongyu, CUI Hejing, et al. Low-energy helium-ions irradiation induced morphology and crystalline evolution of tungsten[J]. Nuclear Techniques, 2017, 40(10): 100201. DOI:10.11889/j.0253-3219.2017.hjs.40.100201 |
| [15] |
Wolfer W G. Spectroscopies for environmental studies of actinide species[M]. New Mexico: Los Alamos Science, 2000, 274-285.
|
| [16] |
Natarajan V, Seshagiri T K, Veeraraghavan R, et al. Radiation effects in plutonium and carbonate co-doped calcium hydroxy apatite:an EPR study[J]. Journal of Radioanalytical & Nuclear Chemistry, 2003, 256(3): 445-449. DOI:10.1023/A:1024591414217 |
| [17] |
Jutier F, Griveau J C, Colineau E, et al. Influence of self-irradiation damages on the superconducting behaviour of Pu-based compounds[J]. Physica B Condensed Matter, 2005, s359-s361: 1078-1080. DOI:10.1016/j.physb.2005.01.292 |
| [18] |
Elliott R O, Olsen C E. Comparison of self-irradiation effects in alpha plutonium enriched and unenriched in 238Pu[J]. Journal of Applied Physics, 1964, 35(6): 1925-1931. DOI:10.1063/1.1713771 |
| [19] |
Liu X J, Zhao Y L, Lu Y, et al. Steady-state dynamical phase diagram calculation of U-Nb binary system under irradiation:ballistic effect[J]. Journal of Nuclear Materials, 2014, 451(1-3): 366-371. DOI:10.1016/j.jnucmat.2014.04.028 |
| [20] |
Cahn J W, Hilliard J E. Free energy of a nonuniform system Ⅰ:interfacial free energy[J]. Journal of Chemical Physics, 1959, 31(3): 688-699. DOI:10.1063/1.1744102 |
| [21] |
Russell K C. Phase stability under irradiation[J]. Progress in Materials Science, 1984, 28(3): 229-434. DOI:10.1016/0079-6425(84)90001-X |
| [22] |
Was G S. Fundamentals of radiation materials science[M]. New York: Springer, 2007, 155-184.
|
| [23] |
胡赓祥, 蔡珣, 戎咏华. 材料科学基础[M]. 上海: 上海交通大学出版社, 2006, 108-222. HU Gengxiang, CAI Xun, RONG Yonghua. Fundamentals of materials science[M]. Shanghai: Shanghai Jiao Tong University Press, 2006, 108-222. |
| [24] |
Ravishankar N, Abinandanan T A, Chattopadhyay K. Application of effective potential formalism to mechanical alloying in Ag-Cu and Cu-Fe systems[J]. Materials Science & Engineering A, 2001, s304-306(00): 413-417. DOI:10.1016/S0921-5093(00)01484-2 |
| [25] |
Uberuaga B P, Valone S M, Baskes M I. Accelerated dynamics study of vacancy mobility in δ-plutonium[J]. Journal of Alloys & Compounds, 2006, 444-445(2007): 314-319. DOI:10.1016/j.jallcom.2006.10.083 |
| [26] |
Berlu L, Jomard G, Rosa G, et al. Computer simulation of point defects in plutonium using MEAM potentials[J]. Journal of Nuclear Materials, 2008, 372(2-3): 171-176. DOI:10.1016/j.jnucmat.2006.11.016 |
| [27] |
Valone S M, Baskes M I, Stan M, et al. Simulations of low energy cascades in fcc Pu metal at 300 K and constant volume[J]. Journal of Nuclear Materials, 2004, 324(1): 41-51. DOI:10.1016/j.jnucmat.2003.09.006 |
| [28] |
Kubota A, Wolfer W G, Valone S M, et al. Modeling of aging in plutonium by molecular dynamics[J]. Nuclear Instruments & Methods in Physics Research, 2003, 202(202): 82-87. DOI:10.1007/s10820-007-9057-x |
| [29] |
Ao B Y, Wang X L, Chen P H, et al. Energy calculation of point defects in plutonium by embedded atom method[J]. Acta Physica Sinica, 2010, 59(7): 4818-4825. DOI:10.7498/aps.59.4818 |
| [30] |
Yu X H, Zhan Z L, Rong J, et al. Vacancy formation energy and size effects[J]. Chemical Physics Letters, 2014, 600(600): 43-45. DOI:10.1016/j.cplett.2014.03.046 |
| [31] |
Sizmann R. The effect of radiation upon diffusion in metals[J]. Journal of Nuclear Materials, 1978, s69-70(1-2): 386-412. DOI:10.1016/0022-3115(78)90256-8 |
| [32] |
Elliott R O, Olsen C E. Comparison of self-irradiation effects in alpha plutonium enriched and unenriched in 238Pu[J]. Journal of Applied Physics, 1964, 35(6): 1925-1931. DOI:10.1063/1.1713771 |
| [33] |
Troshev A V, Lyasota A M. Effect of self-irradiation on the parameters of the α→β transformation of unalloyed plutonium[J]. Physics of Metals & Metallography, 2010, 109(6): 621-625. DOI:10.1134/S0031918X10060086 |
| [34] |
Foltyn E M, Clinard Jr F W, Rankin J, et al. Self-irradiation effects in 238Pu-substituted zirconolite Ⅱ:effect of damage microstructure on recovery[J]. Journal of Nuclear Materials, 1985, 136(1): 97-103. DOI:10.1016/0022-3115(85)90035-2 |
