2. 南华大学 核科学技术学院 衡阳 421001
2. School of Nuclear Science and Technology, University of South China, Hengyang 421001, China
基于蒙特卡罗算法模拟光子和电子的耦合输运,得到非均匀介质中的剂量分布,已成为一种公认的最为准确的剂量计算方法[1-3]。使用蒙特卡罗算法模拟医用加速器剂量分布的关键是提高模拟精度,使之与测量剂量之间的误差尽可能小[4]。模拟剂量的准确性,依赖于精确的加速器蒙特卡罗模型。其中入射电子线参数,即平均能量、径向强度分布以及平均角展宽,对百分深度剂量及离轴剂量有一定影响[5-9],确定其准确值是保证模拟结果精确的前提条件。本文根据10 cm×10 cm射野下电子线参数对剂量分布的影响特性,提出一种确定电子线参数的可行性方法。
1 医用直线加速器治疗头的蒙特卡罗模拟及剂量测量 1.1 EGSnrc程序模拟步骤蒙特卡罗程序EGSnrc[10]模拟医用直线加速器剂量沉积分为两步:首先在子程序BEAMnrc[11]中模拟粒子在加速器治疗头中的耦合输运,得到相空间文件(用于存储粒子在特定平面处的能量、位置坐标、入射方向、权重等信息);随后将相空间文件作为子程序DOSXYZnrc[12]中的输入源,模拟粒子的剂量沉积,得到水模体中各位置处的剂量。
1.2 BEAMnrc加速器模型根据厂商提供的瓦里安IX加速器部件的几何尺寸和材料,使用BEAMnrc程序中的SLABS、CONS3R、FLATFILT、CHAMBER、MIRROR、JAWS和SLABS组件分别模拟靶、初级准直器、均整器、监督电离室、射野镜、次级准直器以及空气层。射野为开野,大小10 cm×10 cm,多叶准直器没有建模[13]。相空间文件选择在垂直于粒子出射方向、源皮距为100 cm的平面处,方差减少技术选择直接韧致辐射分裂[14] (Directional Bremsstrahlung Splitting, DBS),电子截止能量为0.7 MeV,光子截止能量为0.01 MeV,韧致辐射角展度抽样选择Simple。入射电子束假设服从高斯径向强度分布(BEAMnrc 19号源)。由于使用单能电子线或者具有能谱分布的电子线得到的剂量分布相差很小,本文模拟所选用的电子线均为单能电子线;径向强度分布由高斯分布的标准差给出,用σ表示,在模拟百分深度剂量与离轴剂量时均选择圆形电子束,所不同的是在模拟百分深度剂量时,σ大小保持0.1 cm不变,在模拟离轴剂量时,σ取值为0~0.2 cm;平均角展宽在能量及径向强度分布值确定之前始终设置为0°,只在最后过程中改变其大小,以获得各深度处更为精确的离轴剂量。
1.3 DOSXYZnrc中水模设置将相空间文件作为DOSXYZnrc程序中的输入源(2号源),计算水模中剂量的沉积。三维坐标系为笛卡尔坐标系,其中Z轴为粒子入射方向,垂直向下,原点在水模上表面的中心点位置。水模体积为40 cm×40 cm×40 cm,划分成许多大小不同的体素。计算百分深度剂量时,体素在X和Y方向上的长度均为1 cm,在Z轴方向上体素长度并不相同:在剂量建成区长度为0.2 cm,包含最大剂量点的体素长度为0.6 cm,水模2 cm深度以下的体素长度为0.5 cm,剂量不确定度在0.4~28 cm深度范围内均小于或等于1%。计算离轴剂量时,水下1.5 cm、5 cm、10 cm、20 cm、30 cm深度处的各体素在X、Y、Z轴方向上的长度均相等,分别为0.4 cm、1 cm、0.4cm,主剂量区的离轴剂量在各深度处的统计不确定度均在1%以下,在30 cm深度处的不确定度则在1.6%以下。电子和光子截止能量与BEAMnrc设置相同。电子步长算法和边界穿越算法分别使用PRESTA-Ⅱ和EXACT。
1.4 百分深度剂量及离轴剂量测量深度剂量及离轴剂量采用电离室(Semiflex 31010)进行测量,这是由于对于光子束,采用电离室测量的数据更为准确[15]。电离室由三维水箱(MP3)中扫描系统(MEPHYSTO-mc2)控制的电机进行驱动。水模体的分辨率0.1 mm,定位精度±0.1 mm。扫描电离室的有效体积0.125 cm3,腔体直径5.5mm。使用电离室测量各位置处的输出剂量率,射野中心轴不同深度处的剂量率归一到最大剂量深度处的剂量率;各深度处的离轴剂量率按下文说明归一到相应位置处的剂量率。
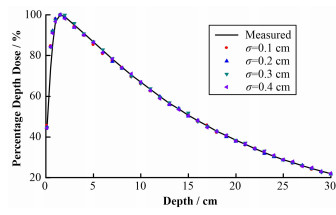
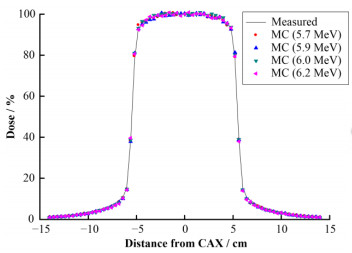
2 径向强度分布对百分深度剂量影响及电子线能量对离轴剂量影响模拟与测量的深度剂量均在水下1.5 cm深度处的最大剂量点处进行归一化,电子线能量固定,不同径向强度分布得出的模拟剂量与测量剂量如图 1所示,径向强度在0.1~0.4 cm改变时,对百分深度剂量的影响可以忽略。径向强度分布为固定值时,不同能量得到的水下10 cm深度处的离轴剂量如图 2所示,所有模拟与测量的离轴剂量在X轴中心处的剂量点进行归一化,4个能量值得到的离轴剂量没有明显区别且在主剂量区及半影区均与测量剂量有很好的符合度。由此电子线能量通过匹配百分深度剂量确定,而径向强度分布可通过离轴剂量确定。
|
图 1 径向强度分布不同时模拟与测量得到百分深度剂量曲线 Figure 1 Percentage depth dose curves calculated with different radial intensities compared with measured doses |
|
图 2 不同能量时模拟与测量的离轴剂量曲线 Figure 2 Dose profiles calculated with different energies compared with measured doses |
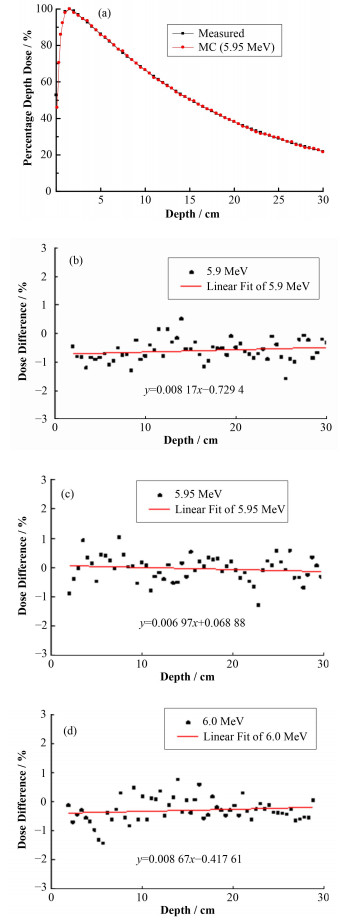
当入射电子线平均能量为5.95 MeV时,模拟与测量的百分深度剂量之间的剂量差异在各深度处均小于0.8%,二者有非常高的符合度,如图 3(a)所示。为得到更为精确的最佳能量值,对各能量值计算出的剂量与测量值之间的百分深度剂量差进行最小二乘拟合,所得到的拟合曲线斜率越接近于0,截距绝对值越小,则说明电子线能量越为准确,模拟与测量的剂量越为接近。图 3(b)、(c)、(d)为能量5.9 MeV、5.95 MeV及6.0 MeV时的百分剂量差异拟合曲线,可以看出,能量为5.95 MeV时得到的剂量分布最为理想,对于5.4~6.5 MeV内其他能量值对应的剂量差异也进行了拟合,但为减少图表量,没有在文中显示。
|
图 3 电子线能量为5.95 MeV时模拟与测量的百分深度剂量曲线及不同能量对应的百分剂量差 (a)百分深度剂量,(b)-(d)百分剂量差异 Figure 3 Measured and calculated depth doses for 5.95 MeV electron energy and dose differences between simulation and measurement for different energies (a) Percentage depth dose, (b)-(d) Percentage dose differences |
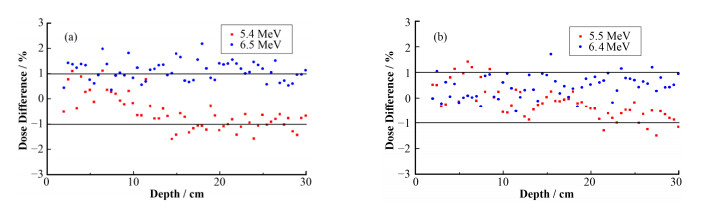
电子线能量在标称能量附近一定范围内变化时,百分深度剂量变化较小,但超出该范围时,模拟与测量的深度剂量差异变大,此时的电子线能量不适用于以后的模拟工作,图 4(a)、(b)显示了两组能量边界值分别为5.4 MeV、6.5 MeV及5.5 MeV、6.4 MeV时的百分剂量差,可以看出,(a)组在水模下有较多位置处的局部剂量差大于1%,而(b)组能量对应的剂量差异大部分在1%以下。由此可见,电子线能量在5.5~6.4 MeV范围内时,模拟的百分深度剂量较为准确。
|
图 4 电子线能量不同时百分剂量差异 (a) 5.4 MeV、6.5 MeV,(b) 5.5 MeV、6.4 MeV Figure 4 Dose differences between calculated and measured percentage depth doses for different electron energies (a) 5.4 MeV, 6.5 MeV, (b) 5.5 MeV, 6.4 MeV |
有关电子线能量对百分深度剂量影响的研究中,Tzedakis等[16]得出对于5 MeV、6 MeV和7 MeV的电子线能量,最大百分剂量差分别为1.7%、0.8%和1.8%,可见能量值超出一定范围后,模拟的剂量与测量值会出现较大偏差。在本研究中,当能量值大于6.4 MeV或小于5.5 MeV时,有较多深度处的百分剂量差大于1%。Chibani等[17]发现当电子线能量在厂商提供的能量值上下0.2 MeV间隔内波动时,百分深度剂量的变化不明显。当能量在5.5~6.4 MeV内变化时,直接观察剂量分布无法得出理想的电子线能量,因此在本文中采用最小二乘拟合方法[18]确定最优电子线能量。当电子线能量为5.95 MeV时,模拟与测量的剂量最为接近。
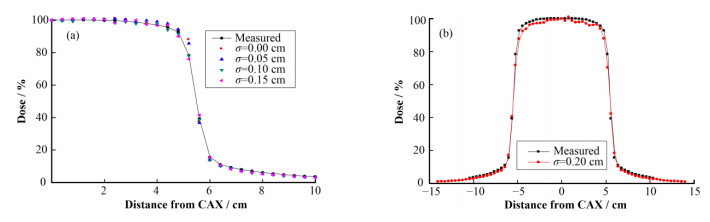
3.2 径向强度分布图 5(a)是水下10 cm深度处的离轴剂量,当径向强度分布值小于0.2 cm时,模拟与测量的剂量在主剂量区差别不大,但在半影区,二者之间有较大的差异,因此本文采用匹配半影区剂量的方法来确定径向强度分布的大小。表 1是不同径向强度分布值得到的半影区剂量与测量值的百分差异,当σ= 0.1cm时,剂量误差最小。图 5(b)表明当径向强度开始大于0.2 cm时,模拟与测量的剂量开始出现明显的误差,在确定径向强度大小时,建议σ在小于0.2 cm的范围内寻找。
| 表 1 径向强度分布不同时离轴5.2 cm处剂量点模拟值与测量值局部剂量差异 Table 1 Local dose differences between calculated and measured dose at a point with 5.2 cm off-CAX distance |
|
图 5 径向强度分布不同时模拟与测量的离轴剂量曲线(a) σ < 0.2 cm,(b) σ=0.2 cm Figure 5 Dose profiles calculated with different radial intensities compared with measured doses (a) σ < 0.2 cm, (b) σ=0.2 cm |
电子线径向强度分布对离轴剂量有很明显影响。Sheikh-Bagheri等[5]对0.01~0.20 cm范围内的径向强度分别计算出离轴比因子,将其与σ=0.10 cm得出的因子对比后发现,径向强度较小或较大时(σ接近0 cm或0.19 cm),二者在远离中心轴处存在明显差异,这表明径向强度分布对主剂量区域外的剂量点有较明显影响,此结论与本文中的研究结果一致。在Chibani的研究中,当σ在0.04~0.12 cm范围内变化时,主剂量区的离轴剂量与测量值相比差距很小,在本研究中,σ的取值范围为0~0.19 cm,在此范围得到的离轴剂量与测量值在主剂量区的差距同样很小,有较好的符合度。根据以上两个研究中的结论,可以通过半影匹配而不是主剂量区匹配来确定径向强度分布。
半影区包括几何半影、穿透半影、散射半影,因此半影区剂量主要包括放射源边缘形成的剂量、准直器穿透剂量以及病人体内的散射剂量。在研究中认为半影区剂量改变只是由于几何半影剂量改变引起的,这是因为在模拟过程中加速器机头及水模体始终保持不变,穿透半影及散射半影形成的剂量近似认为没有变化。几何半影区剂量变化主要是由于径向强度不同时电子线的形状有一定变化,导致打靶时产生的散射光子在半影区沉积的剂量有一定差异。半影区处于剂量梯度变化很大的位置,确保其剂量准确对于保护器官具有重要意义,通过匹配半影区剂量,在保证主剂量区剂量准确的同时,可以保证半影区剂量准确性。
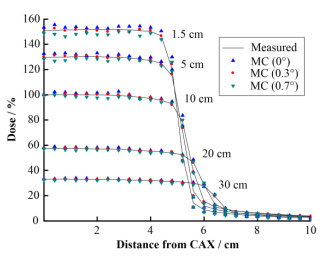
3.3 平均角展宽电子线平均能量5.95 MeV,径向强度分布为0.1 cm,水下各深度模拟与测量的剂量全部归一化到10 cm深度处坐标轴上的中心剂量点,不同角展宽得到的各深度离轴剂量如图 6所示。当角展宽为0°时,各深度处模拟的剂量值略微高于测量值;角展宽为0.7°时,模拟值较测量值偏低。通过调整角展宽为0.3°,得到的各深度处的剂量曲线与测量得到的剂量曲线匹配性要优于上述二者,局部剂量差异基本在1%以内,得到的模拟值更为精确。
|
图 6 平均角展宽不同时各深度处模拟与测量的离轴剂量曲线 Figure 6 Dose profiles calculated with different mean angular spreads compared with measured doses |
平均角展宽是Z轴与粒子入射方向之间的微小夹角,由电子径向强度分布最大值的半值确定,因此,其对离轴剂量也有一定影响。径向强度分布较大的电子线产生的韧致辐射光子在经过初级准直器时更易被阻挡,当平均角展宽变大时,离轴剂量略微变小。通过调整平均角展宽为0.3°,模拟的离轴剂量在各深度处均与测量值取得了较好的符合度。
4 结语确定模拟所需电子线参数是保证模拟结果准确的重要一步,这些参数通常不能直接得到,但是却对剂量分布有非常重要的影响。根据10 cm×10 cm射野下剂量特性的研究,本文提出了一种确定电子线参数的方法:首先,根据模拟与测量的百分深度剂量,采用最小二乘拟合,确定出最优电子线能量,并在随后的模拟过程中保持不变;其次,根据半影区剂量匹配,确定出使模拟剂量最为准确的径向强度分布大小;最后,通过调整平均角展宽,使各深度处的离轴剂量与测量值有更好的符合度。对于10cm×10 cm射野,所得结论如下:
1) 电子线能量和径向强度分布可以分别独立确定。2)通过半影匹配,可以得到更为精确的离轴剂量。3)调整平均角展宽可以使各深度处模拟离轴剂量与测量值有更好的符合度。4)电子线能量及径向强度分布分别建议在5.5~6.4 MeV和0.05~ 0.15cm范围内寻找。
| [1] |
Rogers D W O, Bielajew A F. Monte Carlo techniques of electron and photon transport for radiation dosimetry[J]. Dosimetry of Ionizing Radiation, 1990, 3(1): 427-539. |
| [2] |
Andreo P. Monte Carlo techniques in medical radiation physics[J]. Physics in Medicine and Biology, 1991, 36(7): 861-920. DOI:10.1088/0031-9155/36/7/001 |
| [3] |
Demarco J J, Solberg T, Smathers J B. A CT-based Monte Carlo simulation tool for dosimetry planning and analysis[J]. Medical Physics, 1998, 25(1): 1-11. DOI:10.1118/1.598167 |
| [4] |
Chetty I J, Curran B, Cygler J E, et al. Report of the AAPM task group No.105:issues associated with clinical implementation of Monte Carlo-based photon and electron external beam treatment planning[J]. Medical Physics, 2007, 34(12): 4818-1853. DOI:10.1118/1.2795842 |
| [5] |
Sheikh-Bagheri D, Rogers D W O. Sensitivity of megavoltage photon beam Monte Carlo simulations to electron beam and other parameters[J]. Medical Physics, 2002, 29(3): 379-390. DOI:10.1118/1.1446109 |
| [6] |
Pena J, Gonzalez-Castano D M, Gomez F. Automatic determination of primary electron beam parameters in Monte Carlo simulation[J]. Medical Physics, 2007, 34(3): 1076-1084. DOI:10.1118/1.2514155 |
| [7] |
Wang L L W, Leszczynski K. Estimation of the focal spot size and shape for a medical linear accelerator by Monte Carlo simulation[J]. Medical Physics, 2007, 34(2): 485-488. DOI:10.1118/1.2426407 |
| [8] |
Sham E, Seuntjens J, Devic S, et al. Influence of focal spot on characteristics of very small diameter radiosurgical beams[J]. Medical Physics, 2008, 35(7): 3317-3330. DOI:10.1118/1.2936335 |
| [9] |
韩俊杰, 朱金汉, 张白霖, 等. 医用直线加速器主要部件对X射线能谱的影响[J]. 核技术, 2015, 38(10): 100202. HAN Junjie, ZHU Jinhan, ZHANG Bailin, et al. Effects of main components of clinical linac on X-ray energy spectra[J]. Nuclear Techniques, 2015, 38(10): 100202. DOI:10.11889/j.0253-3219.2015.hjs.38.100202 |
| [10] |
Kawrakow I. Accurate condensed history Monte Carlo simulation of electron transport Ⅰ:EGSnrc, the new EGS4 version[J]. Medical Physics, 2000, 27(3): 485-498. DOI:10.1118/1.598917 |
| [11] |
Rogers D W O, Walters B R B, Kawrakow I. Beamnrc users manual[M]. Ottawa: National Research Council Canada, 2009, 18-114.
|
| [12] |
Walters B R B, Kawrakow I, Rogers D W O. Dosxyznrc users manual[M]. Ottawa: National Research Council Canada, 2009, 10-70.
|
| [13] |
熊绮丽, 石勇, 徐刚, 等. TrueBeam加速器多叶准直器射野剂量学特性[J]. 核技术, 2015, 38(10): 100203. XIONG Qili, SHI Yong, XU Gang, et al. Dosimetry characteristics of muti-leaf collimator field for TrueBeam[J]. Nuclear Techniques, 2015, 38(10): 100203. DOI:10.11889/j.0253-3219.2015.hjs.38.100203 |
| [14] |
Kawrakow I, Rogers D W O, Walters B R. Large efficiency improvements in BEAMnrc using directional bremsstrahlung splitting[J]. Medical Physics, 2004, 31(10): 2883-2898. DOI:10.1118/1.1788912 |
| [15] |
Cao Y, Yang X Y, Yang Z, et al. Superficial dose evaluation of four dose calculation algorithms[J]. Radiation Physics and Chemistry, 2016, 2(1): 1-6. DOI:10.1016/j.radphyschem.2016.02.032 |
| [16] |
Tzedakis A, Damilakis J E, Mazonakis M, et al. Influence of initial electron beam parameters on Monte Carlo calculated absorbed dose distributions for radiotherapy photon beams[J]. Medical Physics, 2004, 31(4): 907-913. DOI:10.1118/1.1668551 |
| [17] |
Chibani O, Moftah B, Ma C M C. On Monte Carlo modeling of megavoltage photon beams:a revisited study on the sensitivity of beam parameters[J]. Medical Physics, 2011, 38(1): 188-201. DOI:10.1118/1.3523625 |
| [18] |
Almberg S S, Frengen J, Kylling A, et al. Monte Carlo linear accelerator simulation of megavoltage photon beams:independent determination of initial beam parameters[J]. Medical Physics, 2012, 39(1): 40-47. DOI:10.1118/1.3668315 |


